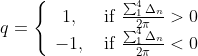光学算法——经典枝切法（解包裹算法）

作者：Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

注：本文所讲内容为本人硕士毕业论文：《基于干涉图像质量分析的激光干涉仪抗振技术研究》，如有引用需要标注来源哈，如有疑问可以评论回复也可以邮箱[email protected]联系我。

 

前言

随着光学技术的不断发展，越来越多的学者从事光学领域的相关学术研究工作，而相位解包裹就是光学相位测量领域中至关重要的一项技术，解缠效果的好坏直接影响了测试的精度和准确性，相位解包裹技术目前也被广泛应用于散斑干涉测量、移相干涉测量、合成孔径雷达、磁共振成像等各个方向。

基于算法实现原理可将解包裹技术大致分为两类：路径跟踪类算法和路径无关类算法。路径跟踪类算法代表用简单行列法、枝切法和质量图法，此类算法的核心在于确定积分结构与路径无关的条件，在满足条件的前提下，通过路径积分算法沿合适的路径还原相位，路径跟踪类算法所求解的相位更加精准；路径无关类代表为各类基于最小二乘原理的解包裹算法，此类算法核心在于运用各类原理或方法进行最小二乘求解，以获得最优的结果数据，常见的求解方法有快速傅里叶变换法（FFT）、迭代法、离散余弦变换法（DCT）等。路径无关类算法所求解相位优化性较好，但并不是精确的相位信息。

本文介绍了其中一种最经典和应用广泛的相位解包裹算法——枝切法，包括一维相位解包裹原理、二维行列法解包裹原理、枝切法原理和算法流程、代码实现。

 

一、一维相位解包裹原理

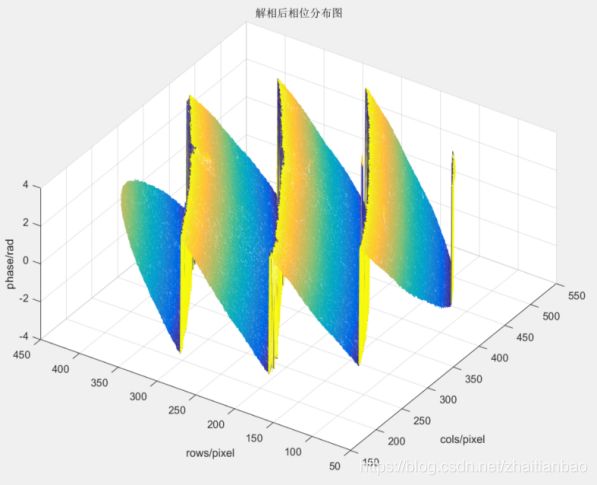
之所以有相位解包裹存在，是因为计算机在进行相位提取时，所得的相位因反正切函数arctan影响，均被折叠在（-π，π）区间内，因而产生区间边缘点的相位突变情况，形成包裹相位，实际效果如图1所示，该图是通过实际测量的干涉图进行计算所得。为了还原其真实的相位信息，必须对包裹相位进行相位解包裹处理，进而通过解完的相位信息计算出所需要的面形信息。

图1 相位提取后的相位分布图

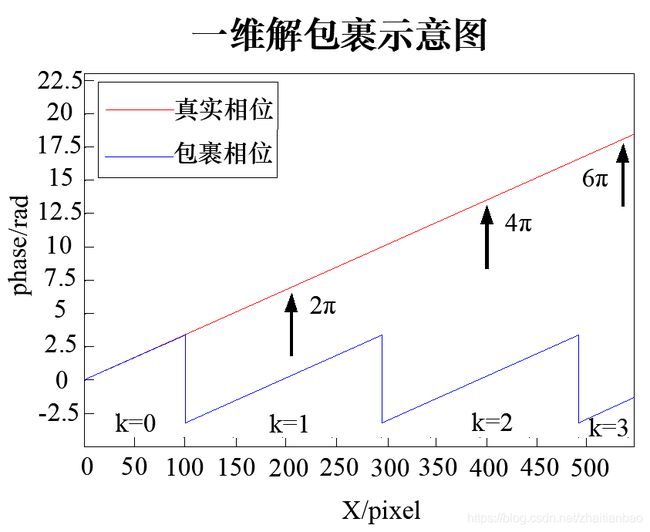
为了更好地理解相位解包裹的原理，先分析最简单的一维解包裹。对一维（只有X轴）的包裹相位而言，其相位折叠于（-π，π）区间内，如图2中蓝线所示，当连续的相位信息超过一个周期后，之后的相位信息骤减降回（-π，π）之间，即出现截断相位。解包裹过程为：从最开始的像素点开始遍历，比较前后两个相位值的大小；如果后相位值比前相位值小超过π，说明出现了截断相位，即相位被包裹，判断间隔k个周期，再令后相位值加上2πk使其回归真实周期；如果后相位值比前相位值大超过π，同理先判断间隔k个周期，再令后相位值减去2πk。

图2 一维解包裹示意图

设包裹相位为，真实相位为，上述算法逻辑用公式(1)表示：

(1)

综上可对一维包裹相位进行解包裹工作，以还原出真实相位信息。

 

二、二维行列法解包裹原理

第一部分讲解了一维相位解包裹的原理，据此可推导出一般意义上的二维解包裹逻辑，先一维展开再逐行或者逐列进一步展开即可实现二维解包裹，这就是行列法的原理，它是二维解包裹算法中最简单的一种，其具体实现过程为：

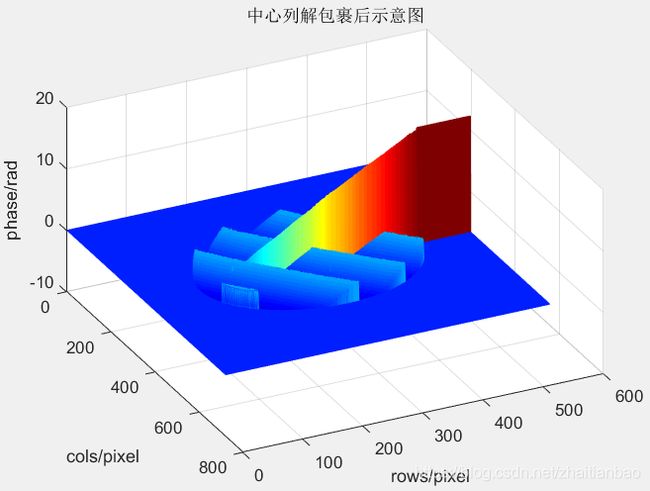
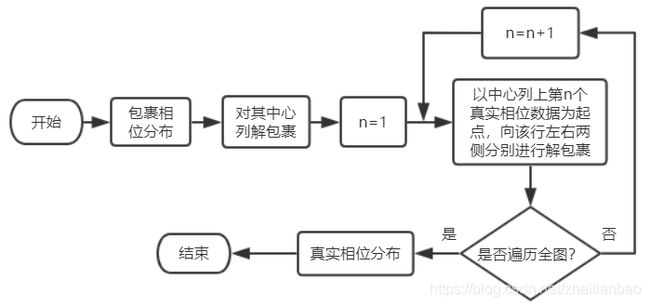
1. 设干涉图大小为R×C，R为干涉图行数，C为干涉图列数。取C/2列为中心列，对该列的相位信息进行一维解包裹处理，如式(1)；此时干涉图中心列的相位信息完成解缠，恢复到真实的相对相位状态，效果图如图3所示；
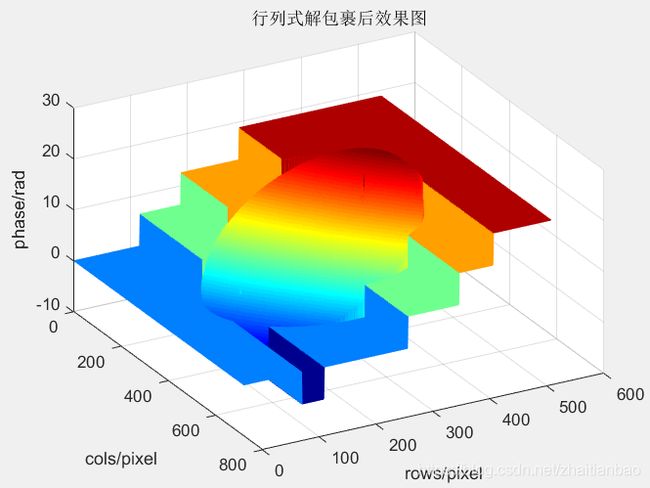
2. 之后，以中心列上的相位数据为起点，分别对每个点的左右两侧的行数据进行解包裹操作，最终可实现全图相位信息的解缠，效果图如图4所示。

图3 中心列解包裹后示意图

图4 行列式解包裹后效果图

该方法运算效率极高，可随意选择路径并依次展开，但是它对噪声的抵抗力较差，当路径中出现异常的数据信息时，并不会将其忽略或跳过，而是沿着错误的信息继续进行解缠操作，这就容易使后续正常的相位信息受到噪声干扰，进而造成误差在路径上持续传播，最终导致相位解包裹失败。

综上，行列式解包裹算法适合对较理想的包裹相位进行解缠，其运算速度极快；当所测面形质量较差时，其解相后相位信息的解缠工作不适用该算法。其算法流程图如图5所示。

图5 行列式解包裹法算法流程图

 

三、枝切法原理和算法流程

若要应对噪声对相位解缠的误差传递，则需对噪声区进行标记和隔离，而经典的枝切式解包裹算法可满足该条件，枝切法的原理：首先，现实环境下因为外在扰动的原因，会使相位数据受到噪声影响而出现非连续点的情况，标记包裹相位图中非连续点作为残差点（正负极性电荷）；其次，将全图的残差点在小范围内进行配对连接，使残差点集合达到极性平衡，该范围一般尽可能小，即枝切线尽可能短；之后，从干涉图中某一非残差点位置开始向四周方向进行解包裹操作，若遇到枝切线上的点则解缠停止，直至全图所有正常相位点完成解缠；最后，分析枝切线周围的正常点相位信息，结合正常信息对枝切线上的相位进行最终的解缠。

其具体实现过程为：

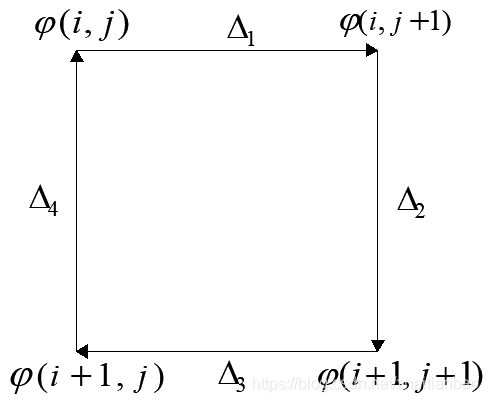
1）判定包裹相位图中残差点位置。设第i行第j列的包裹相位为, 该值处于（-π，π）区间中；定义一个2×2大小的残差点判断窗口，如图6所示，沿顺时针方向计算相邻相位的差值，当差值超过（-π，π）区间时，对其进行缠绕操作W（对该值加减2π，确保其回归到单周期内），用表示该窗口中各个相邻相位间的缠绕差值。

图6 残差点判断窗口示意图

的表达式为公式(2)：

(2)

若窗口中的相位差均在（-π，π）内，则相加为零，说明四个点连续的；反之则为不连续的异常点，此时将（i，j）作为残差点记录下来，残差点的缠绕差值和为2π的正负整数倍，若是正整数倍，则认为该残差点的极性电荷q为正，称作正残差点，值设为1，相反为负残差点，值设为-1：

(3)

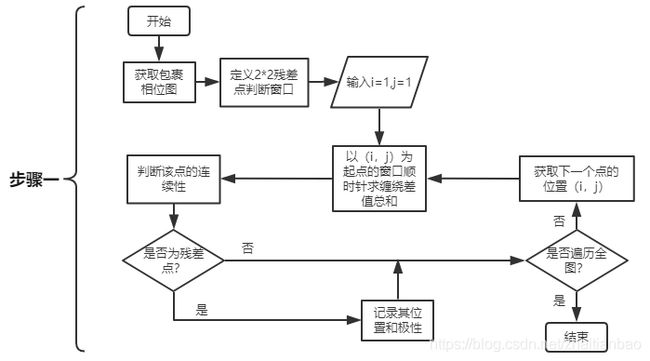
步骤一的算法流程图如图7所示。

图7 枝切法步骤一算法流程图

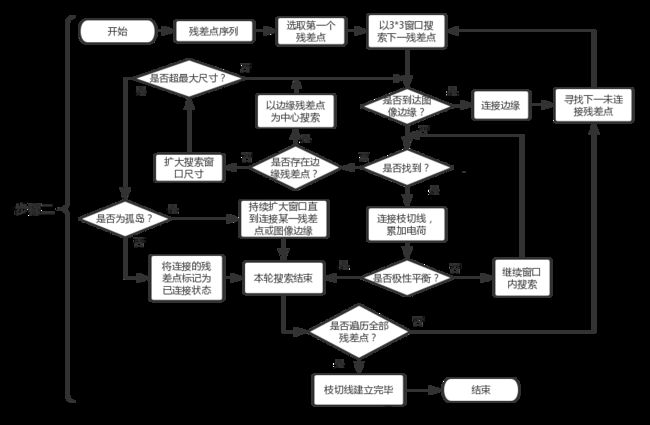
2）将所有残差点按一定顺序排列，选取序列中第一个残差点开始第一轮搜索，以该残差点为中心设置大小为r×r（初始r为3）的搜索窗口来遍历窗口边缘的像素信息，当寻找到另一残差点时连接构成枝切线（两点间近似直线上所有像素点均认为在线上）并判断其极性。两点极性相反即达到平衡态（极性电荷和为0），直接结束该轮搜索工作；若极性相同则未达平衡态，继续寻找下一残差点，当搜索窗口遍历完成时，再以边缘残差点为中心，以同样大小的搜索窗口进行搜寻工作，假如仍未达到平衡态，则扩大搜索窗口尺寸再以开始的中心残差点为起点遍历窗口边缘，尺寸每次增加2（如5×5、7×7）直到达到设置的最大尺寸值（一般为7×7），当完成最大尺寸的遍历工作后无论是否达到平衡，该轮均认为结束。除此之外，当搜索过程中达到图像边缘，同样认为该轮搜索结束。

第一轮结束后，所有连接过的残差点无论整体是否平衡，均标记为已连接状态，若某点在整轮过程中没有任何一个残差点可以与其连接，则继续扩大搜索尺寸直到找到一个可以连接的点（不论正负）并连接，可有效避免某些残差点的遗漏现象发生；再以第二个未连接过的残差点为中心开启下一轮搜索，只搜索未连接过的残差点，以此类推直到全图残差点均被连接完毕，此时相位图的枝切线构建完毕。

步骤二算法流程图如图8所示。

图8 枝切法步骤二算法流程图

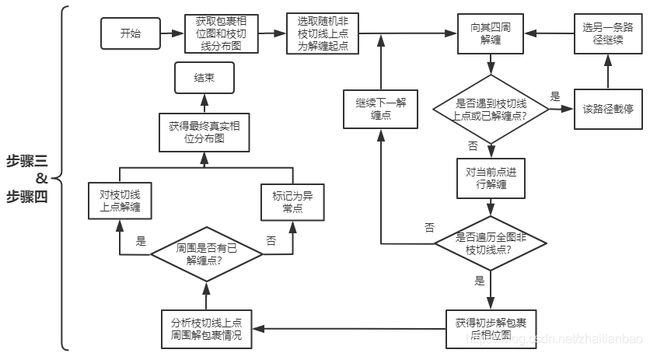
3）开始解包裹：选取某非枝切线上点为起点，分别向其四周开始进行解包裹操作，解包裹之前首先判断其是否为图像边缘点（或掩膜点），再判断其是否已被其他路径进行过解包裹处理，最后判断其是否为枝切线上的点，当上述判断均为否时确认可进行解缠工作；再以四周进行完解包裹的点为起点，同样判断其四周情况，选择合适路径步进；依此类推，可遍历全图正常的包裹相位并完成对其解缠处理，若枝切线闭合则形成“孤岛”。

4）对全图未进行解包裹操作的点作处理。这部分点基本分布在枝切线上，判断点的四周是否存在正常已经解包裹的相位信息。若有则通过正常的相位信息对其进行解缠处理，若无则该点被认为是解缠失败的噪声点，即“异常点”。最终获得真实相位分布图，该相位分布信息有效隔离了噪声带来的误差传递。

步骤三和四的算法流程图如图9所示。

图9 枝切法步骤三&四算法流程图

枝切式解包裹算法能精确地计算出真实的相位信息，相比迭代法之类的解包裹算法要高效许多，且有效避免了某些异常值的误差传递问题，对残差点较少的包裹相位图能起到很好的解包裹作用。其不足之处在于当干涉图中瑕疵过多时，如残差点密集分布，导致枝切线围绕某个区域进行了围绕式连接，进而会使该区域成为一片“孤岛”，其内的相位无法被展开，针对“孤岛”数据，可等第四步枝切线的点计算完再折返回来计算“孤岛”数据。

综上，枝切式解包裹算法能完成绝大多数包裹相位的解缠工作，而那部分少数因包含过多噪声而出现“孤岛”，并导致解缠效果异常的相位信息图，往往从肉眼即可看出较大的瑕疵，不需要应用移相干涉测量技术即可对此类质量差的元件进行过滤。因此，枝切式解包裹算法可以胜任绝大多数场景的解包裹工作。

 

四、代码实现

matlab代码见：https://download.csdn.net/download/zhaitianbao/16236244?spm=1001.2014.3001.5503

C++代码暂不公开分享，如有需要可评论留下邮箱，我将unwrap类中枝切法相关的实现函数单独分享。

 

总结

以上就是本文所讲的内容，简单介绍了相位解包裹的原理和枝切法的算法逻辑。