Anchor-Free模型总结

Anchor-Free综述

一. CornerNet

论文国内地址

1.1 概述

这是第一篇将anchor-free的mAP值刷入COCO榜单的论文，主要贡献是将keypoints的估计方式引入目标检测之中。

主要创新点：

• 使用Heatmap表示目标的坐标left-top、right-bottom
• 增加Offset使得定位更加精确
• 使用Embeddings使得两个关键点匹配
• 使用left、right、top、bottom pooling层增加目标边缘的定位准确度

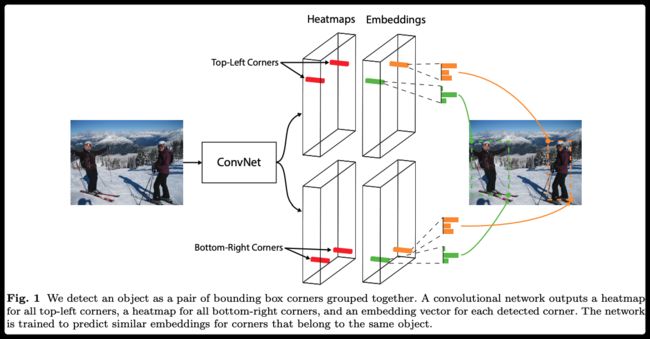
1.2 模块介绍

1.2.1 Heatmap

​ 使用两个Heatmaps表示一个目标的左上角和右下角点，例如：$Left\_top=B\times C\times W\times H$ ，其中 $C$ 表示目标类别，同理右下角点完全相同。对于每一个像素，这是一个分类问题，使用focal-loss去除类别不均衡问题。对于focal-loss而言，类别非0即1，然后Heatmap是使用Gaussian-map生成的，周围的点都是 $value\in [0-1]$。下图展示了，label周围的点实际也是较好的定位点，不应该直接归结为背景，而且给予一定的权重，基于此得重新设计loss函数

其中 $y_{cij}=1$ 的时候和focal-loss相同，$y_{cij}<1$ 的时候使用 $1-y_{cij}$ 作为减少惩罚，如下公式（1）所示
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲L_{d e t}=\frac…

1.2.2 Offset

当前的网络都会进行Downsample or Upsample的操作，使用heatmap最明显的两个缺点：1）计算量比较大，2)精度不准确。对于前者，这里不讨论，可以参考人体关键点期望分布进行解决。后者是这里解决的方案，直接学习一个offset参数去解决
$${\mathbf{o}}_k=\left(\frac{x_k}{n}-\lfloor \frac{x_k}{n}\rfloor ,\frac{y_k}{n}-\lfloor \frac{y_k}{n}\rfloor \right)$$

这里比较简单，不再赘述直接使用SmoothL1-Loss计算即可
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲L_{o f f}=\frac…

1.2.3 Grouping Corners

此处方法参考论文：Associative Embedding

已经学习到多组两个角点的位置，如何将其对应？和Offset处理方式类似，直接使用一个参数（一组参数）去编码当前关键点的组ID信息

比如：Left-top点的heatmap维度为 $B\times C\times W\times H$，Embedding的维度为 $B\times W\times H\times N$ ，其中$C$为种类信息，$N$为维度信息，这样就为每个目标设定了一个长度为$N$的vector信息。当然可以使用$N\times M\times K...$ 等多维度信息去表示。
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲L_{\text {pull …

KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲L_{p u s h}=\fr…

#https://github.com/zzzxxxttt/pytorch_simple_CornerNet/blob/767bf0af3229d9ffc1679aebdbf5eb05671bbc75/utils/losses.py#L34
def _ae_loss(embd0s, embd1s, mask):
  num = mask.sum(dim=1, keepdim=True).float()  # [B, 1]

  pull, push = 0, 0
  for embd0, embd1 in zip(embd0s, embd1s):
    embd0 = embd0.squeeze()  # [B, num_obj]
    embd1 = embd1.squeeze()  # [B, num_obj]

    embd_mean = (embd0 + embd1) / 2

    embd0 = torch.pow(embd0 - embd_mean, 2) / (num + 1e-4)
    embd0 = embd0[mask].sum()
    embd1 = torch.pow(embd1 - embd_mean, 2) / (num + 1e-4)
    embd1 = embd1[mask].sum()
    pull += embd0 + embd1

    push_mask = (mask[:, None, :] + mask[:, :, None]) == 2  # [B, num_obj, num_obj]
    dist = F.relu(1 - (embd_mean[:, None, :] - embd_mean[:, :, None]).abs(), inplace=True)
    dist = dist - 1 / (num[:, :, None] + 1e-4)  # substract diagonal elements
    dist = dist / ((num - 1) * num + 1e-4)[:, :, None]  # total num element is n*n-n
    push += dist[push_mask].sum()
  return pull / len(embd0s), push / len(embd0s)

1.2.4 Corner Pooling

由于两个角点光靠局部位置很难确定，对比mask和bbox的区别。这里使用创新的pooling层去解决这个问题。**其实按照现在流行的做法，使用Non-local、SE模块去处理可能会更好。**做法非常简单，但需要自己写cuda层实现。


KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲t_{i j}=\left\{…

KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲l_{i j}=\left\{…

1.3 总结

此论文是开创性的，位置毋庸置疑。

缺点也是一目了然–>>

二. CenterNet

2.1 概述

基于CornerNet的改进版本，主要贡献是速度快精度准，当时是用在移动端利器

主要创新点：

• 使用中心点代替角点，直接回归长宽
• 使用Offset（CornerNet已经存在）
• 使得增加属性非常容易，比如depth、direction…

2.2 Center-Regression

对于CornerNet来说，回归两个角点+回归Offset+回归分组信息+NMS，显得特别繁琐，而且计算很慢！这里对其进行如下改进：

1. 使用中心点和 $W、H$ 代替两个角点
2. 依然回归Offset对位置精度弥补
3. 去除分组对齐
4. 去除NMS

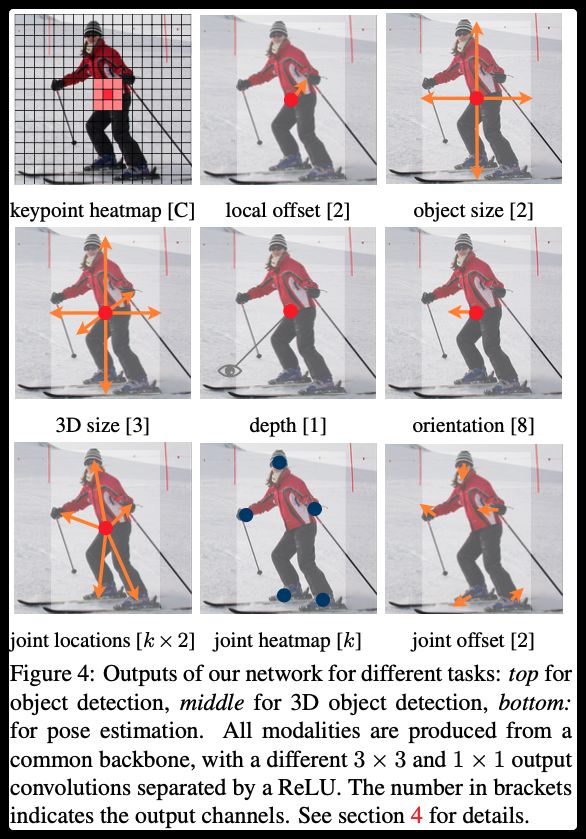
由于其核心是使用目标的中心点进行的操作，所以添加其它属性非常方便，如上图中的方向、关键点、深度…

三. FCOS

3.1. 概述

主要做的贡献如下（可能之前有人已提出）：

1. FPN分阶段回归
2. Center-ness Loss

3.2. 模块介绍

3.2.1 论文思路简介

论文整体比较简单，直接从头读到尾没有什么障碍，好像Anchor-free的文章都比较简单。下面直接以模块介绍。

文章中 $l^{\ast }、b^{\ast }、r^{\ast }、t^{\ast }$ 表示label，$l、b、r、t$ 表示predict

3.3.2 回归形式

文章直接回归 $l、r、b、t、c$ 其中 $c$ 表示种类，前面四个在上图中有表示。

回归采用正负样本形式：

• $featuremap$ 表示回归的特征图（以 $M$ 表示）
• $M_{i,j}$ 表示 $(i,j)$ 个点的特征值
• 将 $M_{i,j}$ 映射到原图，假设当前特征图的总步长是 $S$ （和原图比例），则原图点$P_{i,j}=（\frac{S}{2}+Mi\ast S，\frac{S}{2}+Mj\ast S）$
• $P_{i,j}$ 落入哪个label区域，就负责回归哪个label，算作正样本。落到外部则算作负样本。
• 如果落在重复区域，按照上图的形式（哪个面积小，就负责哪个label）

文章采用FPN结构，用于提高召回率和精确度。参考Anchor-based（不同尺度的Anchor负责不同大小的目标），文章对不同的层进行限制目标大小：其中$M_1、M_2、...M_6=0、64、128、256、512$，按照 $M_i<（l^{\ast }、b^{\ast }、r^{\ast }、t^{\ast }）<M_{i-1}$ 形式进行分配。

最后文章发现一个问题，NMS时候出现很多和最终目标接近的框，我们希望的是：负样本和正样本区分明显，而不是很多接近正样本的框（比如分类，虽然可以正确分类，但是出现很多 $conf=0.45$ 的目标，我们希望出现$con{f}_{pos}=0.99,con{f}_{neg}=0.11$）。

文章通过设置 $center$ 进行控制，对于那些中心偏离的目标进行抑制。我们不仅仅要IOU好，也要center好。文章通过新建一个新的分支进行center-ness进行回归。
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲enterness $^{*}…

3.3 参考文献

• 原始论文
• FCOS改进

四 ATSS

此论文对比anchor-free和anchor-base的区别，从而在anchor-base上提出一套自动计算anchor的工具。使用较少，这里略过。

五.GFLV1

5.1. 论文简介

将目标检测Loss和评价指标统一，提升检测精度。这是一篇挺好的论文，下面会将其拓展到其它领域。

主要做的贡献如下（可能之前有人已提出）：

1. 分类Loss+评价指标
2. Regression分布推广到一般性

5.2. 模块详解

5.2.1 谈谈分布

1. 什么是分布？表示一个数发生的概率，设 $f=P(x)$ 表示分布函数，$f$ 表示发生的概率，$x$ 可能存在的数。1）显而易见，${\int }_{-\infty }^{+\infty }P(x)dx=1$，所有的数存在概率总和为1。 2）$y={\int }_{-\infty }^{+\infty }P(x)\ast xdx$ ，它的整体期望（平均值）肯定是等于目标值的。
2. 什么是 $Dirac$ 分布? reference ，$f=\delta (x-\mu )$ , 当 $x=\mu$ 概率为1，其它都是0。这是什么意思？此分布简称为绝对分布，只要是直接求目标的，都属于此分布。比如：1）直接计算 $one-hot$ 交叉熵 $label=[0,0,0,1]，pred=[0.2,0.1,0.1,0.6]$，我们的目的就是两者相等，其它的值都是不存在的。你问我按照$Delta$ 分布应该其他值为0才对啊，那loss=0（实际loss为什么不是0）怎么回传呢？记住Loss和分布不是一个概念，Loss是我们用一种方式使得结果达到理想分布，分布是一种理想的状态，简单点说 $Loss\to Sample$。2）那么直接进行BBox回归也是一种 $Delta$ 分布，因为都是预测一个值，然后直接和Label进行smoothL1计算Loss。
3. 什么是 $Gaussian$ 分布，这个不多说大家都知道。$Gaussian-YOLO$ 和 $Heatmap$ 都是属于此分布。举个例子：刚开始做关键点（当前小模型人脸也是这样做的）直接使用坐标 $(x，y)$ 进行回归，显然这是属于 $Delta$ 分布的，后面人们将其改进为 $Heatmap$，这就是将分布改为 $Gaussian$，所以称为$Gaussian-Heatmap$ .
4. 什么是任意分布？只满足分布的两个条件，没有具体的公式。直接使用期望和Label进行计算Loss即可。
5. 进一步理解Loss和分布的关系，期望和Label计算Loss（前向推导使用期望做结果），中间概率和期望计算Loss（使得输出按照一定分布进行，容易收敛提高精度）。

---

5.2.2 分类Loss

• 具体由来见：论文作者知乎回答

笔者给出简短说明：

• 先去看一下FCOS论文，其中使用 $center-ness$ 计算预测框质量，两个作用：1）训练时抑制质量较差的框。2）前向计算时用于NMS操作指标。
• 问题来了。。。训练阶段、前向计算、评价指标没有统一？
• 论文魔改一下Focal-Loss、center-ness统一为一个Loss

• 此部分比较简单，基本和FCOS类似

# 代码出自mmdetection
@weighted_loss
def quality_focal_loss(pred, target, beta=2.0):
    """Quality Focal Loss (QFL) is from
    Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes
    for Dense Object Detection
    https://arxiv.org/abs/2006.04388

    Args:
        pred (torch.Tensor): Predicted joint representation of classification
            and quality (IoU) estimation with shape (N, C), C is the number of
            classes.
        target (tuple([torch.Tensor])): Target category label with shape (N,)
            and target quality label with shape (N,).
        beta (float): The beta parameter for calculating the modulating factor.
            Defaults to 2.0.

    Return:
        torch.Tensor: Loss tensor with shape (N,).
    """
    assert len(target) == 2, """target for QFL must be a tuple of two elements,
        including category label and quality label, respectively"""
    # label denotes the category id, score denotes the quality score
    label, score = target

    # negatives are supervised by 0 quality score
    pred_sigmoid = pred.sigmoid()
    scale_factor = pred_sigmoid
    zerolabel = scale_factor.new_zeros(pred.shape)
    loss = F.binary_cross_entropy_with_logits(
        pred, zerolabel, reduction='none') * scale_factor.pow(beta)

    # FG cat_id: [0, num_classes -1], BG cat_id: num_classes
    bg_class_ind = pred.size(1)
    pos = ((label >= 0) & (label < bg_class_ind)).nonzero().squeeze(1)
    pos_label = label[pos].long()
    # positives are supervised by bbox quality (IoU) score
    scale_factor = score[pos] - pred_sigmoid[pos, pos_label]
    loss[pos, pos_label] = F.binary_cross_entropy_with_logits(
        pred[pos, pos_label], score[pos],
        reduction='none') * scale_factor.abs().pow(beta)

    loss = loss.sum(dim=1, keepdim=False)
    return loss

5.2.3 回归Loss

主要包括两个部分：

• $Delta$ 分布推广到任意分布

  • 论文公式（3）是 $Delta$ 分布的期望，公式（4）和（5）是任意分布的期望
  • 直接预测多个（论文设置为16）值，求期望得到最佳值
  • TIPS: 效果肯定比 $Delta$ 分布好，但是计算量会增加。小模型一般不适用，大模型使用较多。

• 限制任意分布

  • 任意分布会过于离散，实际真实的值距离label都不会太远
  • 限制分布范围，论文公式（6）
  • TIPS: 按照公式推导应该效果好（正在推广到关键点检测），使用任意分布的都可以加上试试。

# 代码出自mmdetection
@weighted_loss
def distribution_focal_loss(pred, label):
    """Distribution Focal Loss (DFL) is from
    Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes
    for Dense Object Detection
    https://arxiv.org/abs/2006.04388

    Args:
        pred (torch.Tensor): Predicted general distribution of bounding boxes
            (before softmax) with shape (N, n+1), n is the max value of the
            integral set `{0, ..., n}` in paper.
        label (torch.Tensor): Target distance label for bounding boxes with
            shape (N,).

    Return:
        torch.Tensor: Loss tensor with shape (N,).
    """
    # 完全按照论文公式（6）所示，label是真实值（目标框和anchor之间的偏差，参考FCOS）
    # pred的shape（偏差*分布），如果没有后面的分布，那就变成delta分布
    dis_left = label.long() # label范围[0,正无穷]，感觉这里应该-1然后限制一下范围最好。作者说long()向下取整，但是这解决不了对称问题。
    dis_right = dis_left + 1
    weight_left = dis_right.float() - label
    weight_right = label - dis_left.float()
    loss = F.cross_entropy(pred, dis_left, reduction='none') * weight_left \
        + F.cross_entropy(pred, dis_right, reduction='none') * weight_right
    return loss

5.3. 参考文献

• 原始论文
• 分布参考一
• 分布参考二
• 论文原理理解参考
• 论文代码理解参考

六. GFLV2

6.1 概述

这篇论文非常非常的简单，类似加入了一个全局信息的SENet模块、或者说Non-Local模块，读懂GFLV1之后，马上解决V2的问题。

此方法在小模型上不适合，在大模型上涨点明显。可以进一步推广，此方案用在大模型non-share Head中，而小模型都是共享Head的。