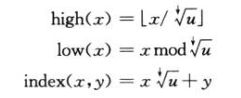常用数据结构对比及其应用场景

目录

• 1.各种表的对比
  参考基本数据结构ADT及其实现
  1.1 三种表
  1.2 表的两种实现（数组、链表）之间的对比
  1.3 栈和队列的应用
• 2.有序数组的二分查找、查找树（搜索树）、跳跃表之间的关系
  2.1 有序数组的二分查找、二叉搜索树与跳跃表
  参考查找树（搜索树）
    2.1.1 三者的本质是一样——快速索引中间元素
    2.1.2 来看看二叉搜索树和跳跃表的定义
  2.2 普通二叉搜索树、伸展树与各种平衡搜索树
    2.2.1 普通二叉搜索树——保证平均情况O(lgn)
    2.2.2 伸展树——保证摊还代价为O(lgn)
    2.2.3 平衡搜索树——带有平衡条件的二叉搜索树（使得树高最坏情况下为O(lgn)）
  2.3 红黑树、1-2-3确定性跳跃表与2-3-4树及2-3树
  参考红黑树专题
    2.3.1 2-3树
    2.3.2 2-3-4树
    2.3.3 基于2-3树的左倾红黑树
    2.3.4 基于2-3-4树的左倾红黑树
    2.3.5 1-2-3确定性跳跃表与2-3-4树
    参考随机算法中的跳跃表
  2.4 二叉搜索树与B树
  参考查找树（搜索树）中的B树
• 3.各种查找数据结构的对比
  3.1 对比
  3.2 各种查找数据结构的应用
    3.2.1 红黑树的应用
    3.2.2 B/B+树的应用
    3.2.3 Trie树（字典树）的应用
    3.2.4 radix树的应用
    3.2.5 哈希算法的应用
• 4.各种堆（优先队列）之间的对比
  参考优先队列——堆
  4.1 堆（优先队列）与搜索树之间的对比
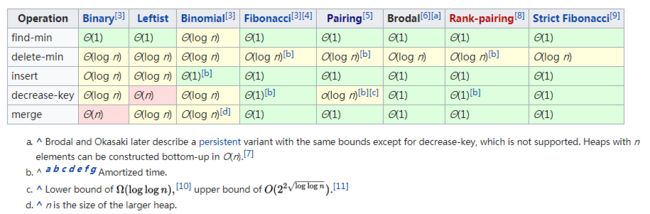
  4.2 各种堆（优先队列）之间的对比
    4.2.1 二叉堆与d-堆（数组实现）——合并困难
    4.2.2 可合并堆——链式结构
    4.2.3 van Emde Boas树——特定条件下突破比较类型堆的限制
    4.2.4 配对堆——结构限制特别少的堆（简单性造就了高效率：合并Θ(1)，DecreaseKey为O(lgn)）
  4.3 堆（优先队列）的应用
    4.3.1 带宽管理（网络路由器）
    4.3.2 离散事件模拟
    4.3.3 Dijkstra算法
    4.3.4 Huffman编码
    4.3.5 Best-first搜索算法（比如A*搜索算法）
    4.3.6 Prim算法
    4.3.7 ROAM triangulation algorithm

1.各种表的对比

1.1 三种表

• 普通表
• 栈是LIFO表（后进先出）
• 队列是FIFO表（先进先出）

1.2 表的两种实现（数组、链表）之间的对比

核心本质只有一条：就是数组需要连续存放，所以需要事先划定一块连续空间大小（提前占有，以防被占用），这才导致了数组链表的所有区别。

• 存放：数组在连续存放的，链表不需要
  因为存放的这个特性导致了下面的区别：
  a. 访问：数组可以常数时间访问第k个元素，链表需要从前向后遍历
  b. 插入和删除：数组需要移动很多元素，链表常数时间即可完成
• 数组一般需要确定大小，链表是动态分配分配
  因此数组一般是从栈中分配空间（广义上的数组，也可以从堆中获取，数组本质上只不过是指针的语法糖衣），链表是从堆中分配空间

1.3 栈和队列的应用

• 栈的对用
  平衡符号（括号的成对匹配）
  后缀表达式
  中缀到后缀的转换
  函数调用
• 队列的应用
  排队论
  任务队列
  在图论中有大量应用
  消息队列
  linux内核进程队列（按优先级排队）

2.有序数组的二分查找、查找树（搜索树）、跳跃表之间的关系

2.1 有序数组的二分查找、二叉搜索树与跳跃表

2.1.1 三者的本质是一样——快速索引中间元素

• 对于一个静态表（不允许插入），对其在初始化是就排序是值得的。
  但是现代应用需要同时能够支持高效的查找和插入两种操作的数据结构（符号表）。
• 怎样找到这种数据结构（符号表）？
  1）高效插入，需要链式结构
  2）二分查找能够快速进行查找（二分查找的高效来自于能够快速通过索引取得任何子数组的中间元素）
  因此将二者结合起来，就是二叉查找树和跳跃表。

2.1.2 来看看二叉搜索树和跳跃表的定义

• （直接将中间元素放在根节点）二叉搜索树中的关键字总是以满足二叉搜索树性质的方式来存储：
  设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么y.key <= x.key。如果y是x右子树中的一个结点，那么y.key >= x.key。

  
  
  

• （结点带有指向中间元素的索引）
  1）k阶结点：带有k个指针的结点。任意k阶上的第i阶（i <= k）指针指向的下一个结点至少具有i阶。
  2）大约有一半的结点是1阶；大约1/4的结点是2阶；一般的，大约1/2^i的结点是i阶结点。按照这个概率分布随机选择结点的阶数。最容易的方法是抛一枚硬币直到正面出现并把抛硬币的总次数作为该节点的阶数。

  
  
  

2.2 普通二叉搜索树、伸展树与各种平衡搜索树

2.2.1 普通二叉搜索树——保证平均情况O(lgn)

• 高度为h的二叉搜索树，查找、插入和删除运行时间均为O(h)。
  二叉搜索树（节点数为n）最坏情况下，高度h = n，随机构造的二叉搜索树的期望高度为O(lgn)。

2.2.2 伸展树——保证摊还代价为O(lgn)

• 当一个结点被访问后，它就要经过一系列AVL树的旋转被放到根上。
  因为许多应用中，当一个结点被访问，它就很可能不久再次被访问到，如果碰到O(N)的结点，没有被移动，那么很难得到O(lgN)摊还时间。
• 保证从空树开始任意连续M次对数的操作最多花费O(MlogN)。虽然这种保证不排除任意一次操作花费O(N)时间。一棵伸展树每次操作的摊还代价是O(logN)。

2.2.3 平衡搜索树——带有平衡条件的二叉搜索树（使得树高最坏情况下为O(lgn)）

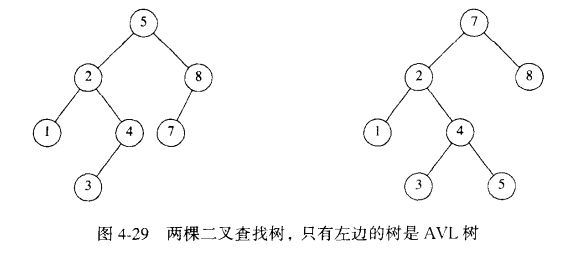
• AVL（Adelson-Velskii和Landis）树：一棵AVL树是其每个结点的左子树和右子树的高度最多差1的二叉查找树。（空树的高度定义为-1）
  在高度为h的AVL树中，最少节点数S(h)由S(h) = S(h-1) + S(h-2) + 1，由n >= S(h)，可以得到h的最大界。

  
  
  

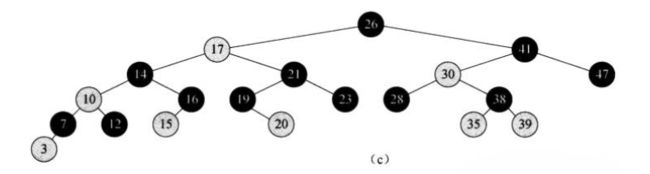
• 一棵红黑树是满足下面红黑性质的二叉搜索树（本质上是基于2-3-4树的红黑树）：
  1）每个结点或是红色的，或是黑色的
  2）根节点是黑色的
  3）每个叶节点NIL时黑色的（这条性质可去掉）
  4）如果一个结点是红色的，则它的两个子节点都是黑色的
  5）对每个结点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色结点
  红黑树确保没有一条路径会比其他路径长处2倍，因而近似于平衡的。（一条最长的路径是黑红相间，一条最短的是全黑，但是黑色结点个数是相等的。）

  
  
  

2.3 红黑树、1-2-3确定性跳跃表与2-3-4树及2-3树

2.3.1 2-3树

• 2-3树是一棵完美平衡的2-3查找树，也即根节点到所有空链接都应该是相同

• 2-3树包含以下结点：
  1）2-结点：含有一个健和两条链接
  2）3-结点：含有两个键和三条链接

  
  
  

2.3.2 2-3-4树

• 2-3-4树是一棵完美平衡的2-3-4查找树，也即根节点到所有空链接都应该是相同

• 2-3-4树包含以下结点：
  1）2-结点：含有一个健和两条链接
  2）3-结点：含有两个键和三条链接
  3）4-结点：含有三个键和四条链接

  
  
  

树高：

• 最坏情况lgN（全是2-结点）
• 最好情况log₄N = 1/2lgN（全是4-结点）
  
  

2.3.3 基于2-3树的左倾红黑树

基于2-3树的左倾红黑树是含有红黑链接并满足下列条件的二叉查找树：

• 红链接均为左链接
• 没有任何一个结点同时和两条红链接相连
• 该树是完美黑色平衡的，即任意空连接到根节点的路径上黑链接数量相同。
• 链接的颜色保存在链接的儿子结点中

对应关系

对应关系

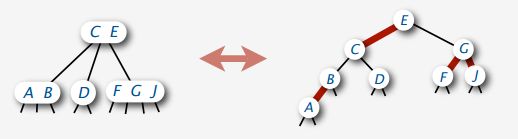
2.3.4 基于2-3-4树的左倾红黑树

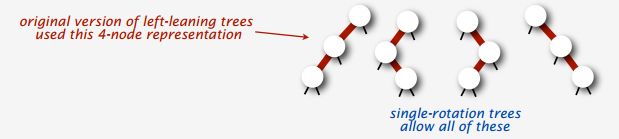
• 基于2-3-4树的左倾红黑树中3-结点和4-结点具有唯一的对应：

  
  
  

• 如下是不允许：

  
  
  

  不允许右倾
  
  
  

  不允许上下连续两个红链接

• 因此基于2-3-4树的左倾红黑树和2-3-4树有唯一的一一对应关系

  
  
  

2.3.5 1-2-3确定性跳跃表与2-3-4树

• 链接：如果至少存在一个指针从一个元素指向另一个元素，则称两个元素是链接的
• 间隙容量：两个在高度为h链接的元素间的间隙容量等于他们之间高度为h-1的元素个数
• 1-2-3确定性跳跃表：每一个间隙（除在头和尾之间可能的零间隙外）的容量为1、2、3。

2.4 二叉搜索树与B树

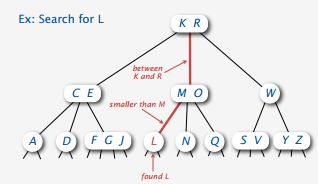
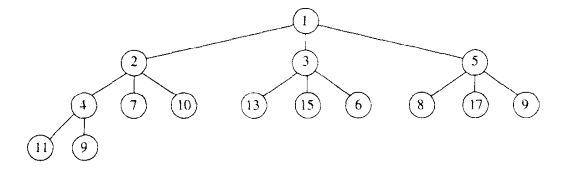
• B树的结点可以有很多孩子。B树以一种自然的方式推广了二叉搜索树。
  如果B树的一个内部结点x包含x.n个关键字，那么结点x就有x.n+1个子域。结点x中的关键字就是分割点，它把结点x中所处理的关键字的属性分割成x.n+1一个子域，每一个子域由x的一个孩子处理。

  
  
  
  
  
  
  
  

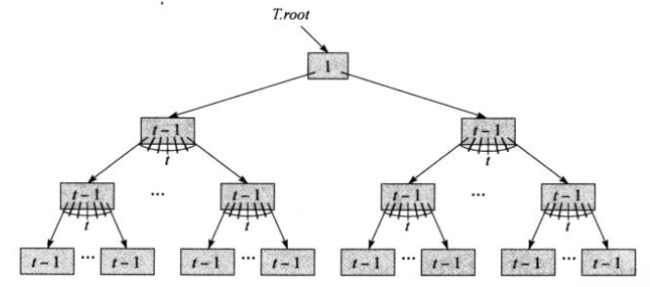
  一棵包含最小可能关键字的B树：

  
  
  

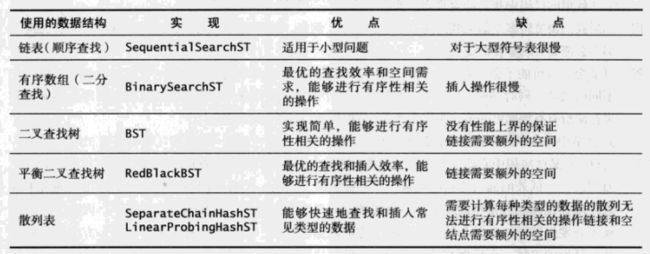
3.各种查找数据结构的对比

3.1 对比

3.2 各种查找数据结构的应用

3.2.1 红黑树的应用

• STL中的map和set的实现
• 著名的linux进程调度[Completely Fair Scheduler]，用红黑树管理进程控制块
• epoll在内核中的实现，用红黑树管理事件块
• nginx中，用红黑树管理timer等
• Java的TreeMap实现

3.2.2 B/B+树的应用

• B和B+主要用在文件系统以及数据库中做索引等，比如Mysql：B-Tree Index in MySql

3.2.3 Trie树（字典树）的应用

• 用在统计和排序大量字符串，如自动机
• trie 树的一个典型应用是前缀匹配，比如下面这个很常见的场景，在我们输入时，搜索引擎会给予提示
• IP选路，也是前缀匹配，一定程度会用到trie

3.2.4 radix树的应用

3.2.5 哈希算法的应用

hash就是一个function，但不要太狭隘，函数的输入不一定得是数字，它还可以是其它所有的二进制数据（字符串、文件等），但必须得有以下特点：
1）同一个输入一定对应着同一个输出；
2）不同输入的输出可能会一样；
下面通过两个常见的使用场景解释可能比较容易理解；

• 应用场景一：构建查找表比如在数据结构中的hash表，输入是key，简单的function如key/N，输出是数组下标，但因为第二个特点，不同key可能会得到相同的输出，所以在各类语言中的hashmap库实现时，会针对的做相应处理，比如从冲突的地方继续做hash运算，直到不冲突为止等；

• 应用场景二：数字签名
  本质还是一样，利用hash 的function对输入做运算，这些运算不局限于上述应用的数字运算，还可以有各类位运算等，所以输入也就不再局限于数字了，而是只要是二进制数据就行，比如字符串、文件等。虽然输入、function、输出形式不一样，上述的两个特点还是成立的。除此之外，为了保证签名的要求，hash function的设置者会针对性的研究function的实现方法，以获得第三个特点：

3）已知输出，不可反推得到输入。

4.各种堆（优先队列）之间的对比

参考优先队列维基百科

4.1 堆（优先队列）与搜索树之间的对比

1）（最大）堆的定义
优先队列是允许至少下列两种操作的数据结构：

• 1）Insert
• 2）DeleteMax 找出、返回和删除优先队列中最大的元素

并且一般的实现都以最坏情形O(lgn)支持上面两个操作。

2）查找树的定义
支持SEARCH(Find)、MINIMUM(FindMin)、MAXIMUM(Find Max)、PREDECESSOR、SUCCESSOR、INSERT和DELETE等集合操作。

3）对比

• 查找树可以实现对的所有操作，并且平衡查找树可以实现最坏情形O(lgn)支持堆的操作（Insert、DeleteMax）
  但是查找树还提供很多其他堆不需要的操作
• 查找树里面的元素是全部有序的，而堆只需要时刻能有效地找出最值，因此无需全部有序
  因此堆的实现可以比查找树更简单

4.2 各种堆（优先队列）之间的对比

4.2.1 二叉堆与d-堆（数组实现）——合并困难

1）二叉堆（数组实现）

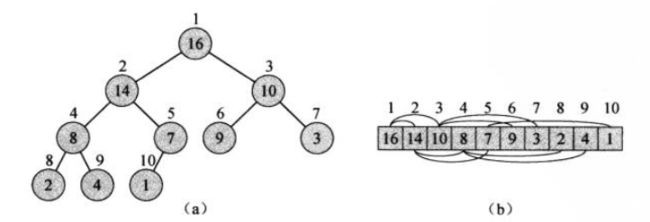
• 二叉堆是一个数组，可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的。而且是从左向右填充。

• 对于最大堆而言：最大元应该在根上，并且任意子树也应该是一个最大堆。也即，除了根以外的所有节点i都要满足：
  A[Parent(i)] >= A[i]

  
  
  

2）d-堆是二叉堆的简单推广（4-堆胜过二叉堆）

3-堆

4.2.2 可合并堆——链式结构

1）二叉堆为什么合并困难？

• 数组实现，合并需要把一个数组拷贝到另一个数组，花费为Θ(n)
• 所有支持高效合并的数据结构都需要使用链式结构（链表、二叉树等），支持高效合并的可合并堆：
  斜堆
  左式堆
  二项队列
  斐波那契堆
  van Emde Boas树

2）斜堆与左式堆

• 斜堆：是具有堆序的二叉树，但是不存在对树的结构限制。不同于左式堆，关于任意结点的零路径长的任何信息都不保留。斜堆的右路径在任何时候都可以任意长。
  因此所有操作的最坏情形为O(N)，但是摊还时间为O(lgn)

• 左式堆：是具有堆序的二叉树，对于堆中的每一个结点，左儿子的零路径长至少与右儿子的零路径长一样大。
  零路径长：定义为任一结点到一个没有两个儿子的结点的最短路径长。（具有0个或1个儿子结点的零路径长尾0，NULL为-1）
  左式堆趋向于加深左路径，所以右路径短。执行合并的时间与右路径的长的和成正比。右路径最长不超过O(lgn)，因此合并的（最坏）时间界为O(lgn)。

  
  
  

• 斜堆——左式堆
  等价于
  伸展树——AVL树

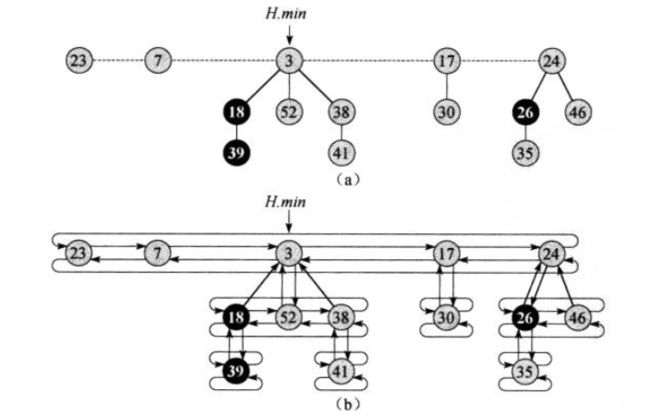
3）二项队列与斐波那契堆——针对斜堆、左式堆的进一步改进

• 斜堆、左式堆以O(lgn)时间支持合并、插入和DeleteMax
  二项队列进行了改进：以最坏O(lgn)时间支持合并、DeleteMax，并且插入平均花费常数时间。
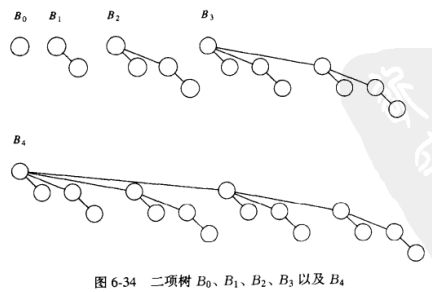
  二线队列是堆序树（二项树）的集合，称为森林。每一个高度上至多存在一棵二项树。高度为0的二项树是一棵单节点树；高度为k的二项树B_k通过将一棵二项树B_k-1附接到另一棵二项树B_k-1的根上而构成。
  

  

• 斐波那契堆：是二项队列的推广
  通过添加两个新的观念：
  a. DECREASE-KEY的一种不同的实现方法：之前的方法是把元素朝向根节点上滤。这种方法不能实现O(1)的摊还时间界，因此需要一种新的方法。（斐波那契堆是直接剪切掉，放到根链表中）
  b. 懒惰合并：只有当两个堆需要合并时才进行合并。类似于懒惰删除。对于懒惰合并，合并是低廉的。但是因为懒惰合并并不实际把树结合在一起，所以DeleteMax操作可能会遇到很多树，从而使得这种操作的代价高昂。 特别地，一次昂贵DeleteMax必须在其前面要有大量非常低廉的合并操作

  
  
  

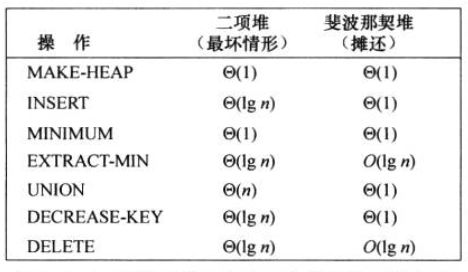
• 斐波那契堆与二叉堆时间对比

  
  
  

4.2.3 van Emde Boas树——特定条件下突破比较类型堆的限制

• 基于比较的各种堆有时间界
  二叉堆、红黑树、斐波那契堆，不论是最坏或摊还情况，至少有一项重要操作需O(lgn)时间。
  原因是这些数据结构都是基于关键字比较来做决定的。基于比较的排序算法的下界是Ω(nlgn)说明至少有一个操作必须Ω(lgn)。因为如果INSERT和EXTRACT-MIN操作均需要O(lgn)，那么可以通过先执行n次INSERT操作，接着再执行n次EXTRACT-MIN操作来实现O(nlgn)时间内对n个关键字的排序。

• 突破基于比较排序堆的是界——线性时间排序的启发
  当关键字是有界范围内的整数是，可以突破排序下界限制。
  同理，van Emde Boas树支持优先队列操作以及一些其他操作（SEARCH、INSERT、DELETE、MINIMUM、MAXIMUM、SUCESSOR、PREDECESSOR），每个操作最坏情况运行时间为O(lglgn)。
  前提是：这种数据结构限制关键字为0~n-1的整数且无重复。

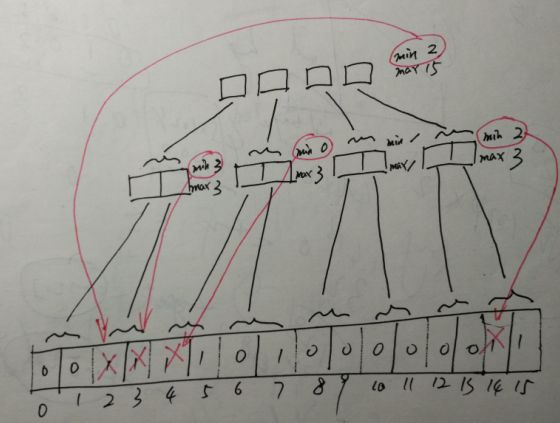
• van Emde Boas树的关键思想
  1）直接寻址
  维护一个u位的数组A[0..u-1]，以存储一个值来自全域{0, 1, 2, ..., u-1}的动态集合。若值x属于动态集合，则A[x]位1；否则为0.
  2）叠加二叉树结构
  在位向量上叠加一棵二叉树，来缩短位向量的扫描。内部节点存储的位是其两个孩子的逻辑或。
  3）叠加的二叉树结构是递归结构，每次递归都以平方根大小缩减全域
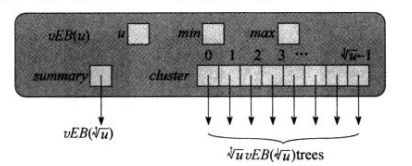
  4）并且一棵vEB树中含有两个属性：
  min存储vEB树中的最小元素（该元素不出现在任何子递归树中）；
  max存储vEB树中的最大元素。

  
  
  
  
  
  
  
  
  
  
  

  如下实例，表示集合{2,3,4,5,7,14,15}：

  
  
  
  
  
  

  image.png

4.2.4 配对堆——结构限制特别少的堆（简单性造就了高效率：合并Θ(1)，DecreaseKey为O(lgn)）

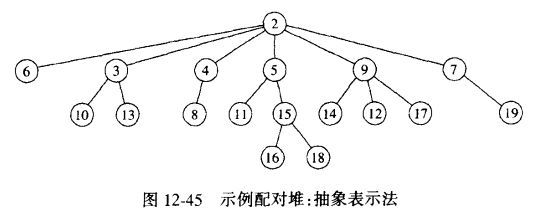
配对堆的基本操作是两个多路堆序树的合并，因此叫配对堆。
配对堆被标示成堆序树：

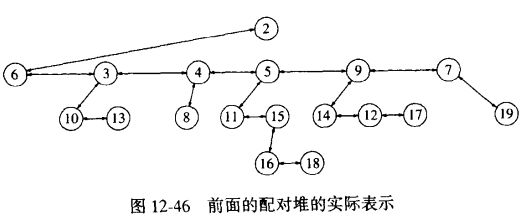
结点的构造：

• LeftChild —— 左儿子
• NextSibling —— 右兄弟
• Prev —— 作为最左儿子，该指针指向其父亲；否则该指针指向其做兄弟

4.3 堆（优先队列）的应用

4.3.1 带宽管理（网络路由器）

4.3.2 离散事件模拟

4.3.3 Dijkstra算法

4.3.4 Huffman编码

4.3.5 Best-first搜索算法（比如A*搜索算法）

4.3.6 Prim算法

4.3.7 ROAM triangulation algorithm

ROAM——Real-time Optimally Adapting Meshes