《PyTorch深度学习实践》--3梯度下降算法

一、.在第二节中的线性模型中，求解w的最优值（使得MSE最小的w）问题。

从图中可以看出：w=2时，MSE最小。（即最优）

二、求解最优w问题的方法

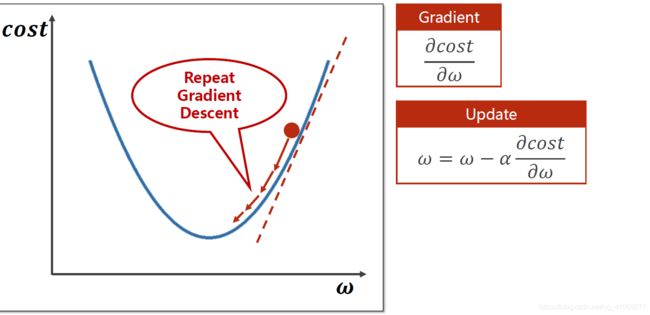
2.1梯度下降（Gradient Descent）算法：

w按梯度下降方向移动，这样一定次数的移动后就会移动到最优解。

（a为学习因子，影响每次移动的步长，越小越精确但时间复杂度也会变高）

通过求导，可以求出具体的表达式，根据表达式就可以写出代码。

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

#mse
def cost(xs,ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost/ len(xs)

#梯度
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2*x*(x*w - y)
    return grad / len(xs)

print('Predict (before training)',4,forward(4))
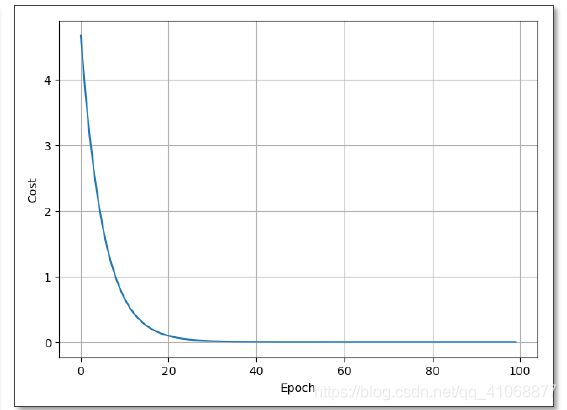
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w -= 0.01 * grad_val //更新w
    print('Epoch:',epoch, 'w=', w, 'loss=', cost_val)
print('Predict (after traning)', 4, forward(4))

 

 

(结果应该是收敛的，如果不收敛可能是a值过大。)

 

 

2.2 随机梯度下降（Stochastic Gradient Descent )

类似梯度下降，但是这里用的是随机某个样本（而不是整体）的梯度。

这样的好处是由于单个样本一般有噪声，具有随机性，可能帮助走出鞍点从而进入最优解。

坏处是计算依赖上次结果，多个样本x无法并行，时间复杂度高。因此会有一个中间的方法，Mini-Batch(或称Batch)。将若干个样本点分成一组，每次用一组来更新w。

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

#mse,单个样本
def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

#梯度,单个样本
def gradient(x, y):
    return 2*x* (x*w - y)

print('Predict (before training)',4,forward(4))
for epoch in range(100):
    for x,y in zip(x_data, y_data):
        grad_val = gradient(x, y)
        w -= 0.01 * grad_val
        print('\tgrad:',x,y,grad_val)
        loss_val = loss(x,y)
    print("progress:", epoch, 'w=', w, 'loss=', loss_val)

print('Predict (after traning)', 4, forward(4))