Pytorch复现STGCN:基于图卷积时空神经网络在交通速度中的预测

1：论文信息

来自IJCAI 2018的一篇论文：《Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting 》

• 原始论文地址链接
• Pytorch代码实现

1.1：论文思路

使用Kipf & Welling 2017的近似谱图卷积得到的图卷积作为空间上的卷积操作，时间上使用一维卷积TCN对所有顶点进行卷积，两者交替进行，组成了时空卷积块，在加州PeMS和北京市的两个数据集上做了验证。论文中图的构建方法并不是基于实际路网，而是通过数学方法构建了一个基于距离关系的网络。

1.2：摘要和引言总结

• 在交通研究中，交通流的基本变量，也就是速度、流量和密度（实际中，还有排队长度，时间占有率，空间占有率，车头时距等多个变量），这些变量通常作为监控当前交通状态以及未来预测的指标。根据预测的长度，主要是指预测时间窗口的大小，交通预测大体分为两个尺度：短期(5~30min)，中和长期预测(超过30min)。大多数流行的统计方法(比如，线性回归)可以在短期预测上表现的很好。然而，由于交通流的不确定性和复杂性，这些方法在相对长期的预测上不是很有效。

• 中长期交通预测上的研究可以分为两类：动态建模和数据驱动的方法。

  • 动态建模方法：使用了数学工具（比如微分方程）和物理知识通过计算模拟来形式化交通问题。为了达到一个稳定的状态，模拟进程不仅需要复杂的系统编程，还需要消耗大量的计算资源。模型中不切实际的假设和化简也会降低预测的精度。因此，随着交通数据收集和存储技术的快速发展，一大群研究者正在将他们的目光投向数据驱动的方法。
  • 数据驱动方法：主要是统计学和机器学习模型。在时间序列分析上，自回归移动平均模型（ARIMA）和它的变形是众多统一的方法中基于传统统计学的方法。但是，这种类型的模型受限于时间序列的平稳分布，不能捕捉时空间依赖关系。因此，这些方法限制了高度非线性的交通流的表示能力。相对传统统计学方法，机器学习可以获得更高精度的预测结果，对更复杂的数据建模，比如k近邻（KNN），支持向量机（SVM）和神经网络（NN）。

• 深度学习方法：深度学习已经广泛且成功地应用于各式各样的交通任务中，并取得了很显著的成果，比如层叠自编码器（SAE）。然而，这些全连接神经网络很难从输入中提取空间和时间特征。而且，空间属性的严格限制甚至完全缺失，这些网络的表示能力被限制的很严重。为了充分利用空间特征，一些研究者使用了卷积神经网络来捕获交通网络中的临近信息，同时也在时间轴上部署了循环神经网络。通过组合LSTM和1维卷积，比如特征层面融合的架构CLTFP来预测短期交通状况。CLTFP是第一个尝试对时间和空间规律性对齐的方法。后来，有学者提出带有嵌入卷积层的全连接网络：ConvLSTM。但是常规卷积操作只适合处理规则化的网络结构，比如图像或者视频，而大多数领域是非结构化的，比如社交网络，交通路网等。此外，RNN对于序列的学习需要迭代训练，这会导致误差的积累。并且还有难以训练和耗时的缺点。

• 针对以上问题和缺陷：该文引入了一些策略来有效的对交通流的时间动态和空间依赖进行建模。为了完全利用空间信息，利用广义图对交通网络建模，而不是将交通流看成各个离散的部分（比如网格或碎块）。为了处理循环神经网络的缺陷，我们在时间轴上部署了一个全卷积结构来加速模型的训练过程。综上所述，该文提出了一个新的神经网络架构-时空图卷积网络，来预测交通状况。这个架构由多个时空图卷积块组成。

• 主要贡献：

  • 该文研在交通研究中第一次应用纯卷积层（TCN）来同时从图结构的时间序列中提取时空信息。
  • 该文提出了一个新的由时空块组成的神经网络结构。由于这个架构中是纯卷积操作，它比基于RNN的模型的训练速度快10倍以上，而且需要的参数更少。这个架构可以让我们更有效地处理更大的路网。
  • 实验在两个真实交通数据集上验证了提出来的网络。这个实验显示出我们的框架比已经存在的在多长度预测和网络尺度上的模型表现的更好

1.3：上述总结

2：正文

2.1：数据处理

文章首先将网格数据改为图数据作为输入，图可以用邻接矩阵来表示，图中的W就是图的邻接矩阵，实验中使用的数据集PeMSD7(M)共有228个数据点，相当于一个具有228个顶点的图，因为这个模型主要是对速度进行预测，所以每个顶点只有一个特征就是：速度。

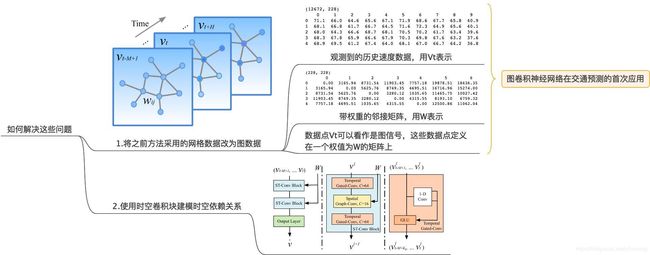
2.2：网络架构

网络架构是本文的重点部分。如下图所示，STGCN有多个时空卷积块组成，每一个都是像一个“三明治”结构的组成，有两个门序列卷积层和一个空间图卷积层在中间。
组成结构：STGCN 有两个ST-Conv Block（淡蓝色部分）快和一个全连接输出layer（绿色部分），其中每个ST-Conv Block块有包括两个时间卷积块（橙色部分）和一个空间卷积块（浅黄色部分）

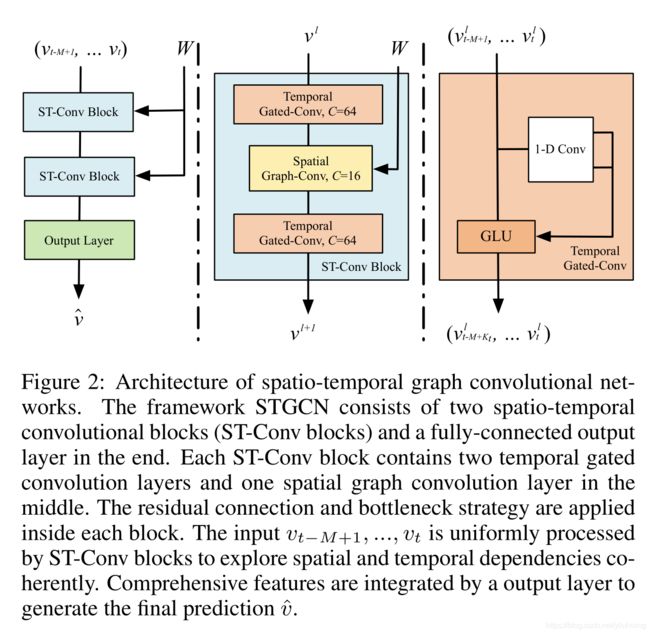
2.3：提取空间特征的图卷积神经网络

提取时间特征的图卷积神经网络，即对应网络结构中的Spatial Graph-Conv 模块。
交通路网是非结构化的图像，为了捕获空间上的相关性，本篇论文采用的是切比雪夫近似与一阶近似后的图卷积公式。只需要看最终的那个卷积公式，其中D为图的度矩阵，A_hat为图的邻接矩阵+单位矩阵，为的是在卷积过程中不仅考虑邻居节点的状态，也考虑自身的状态。

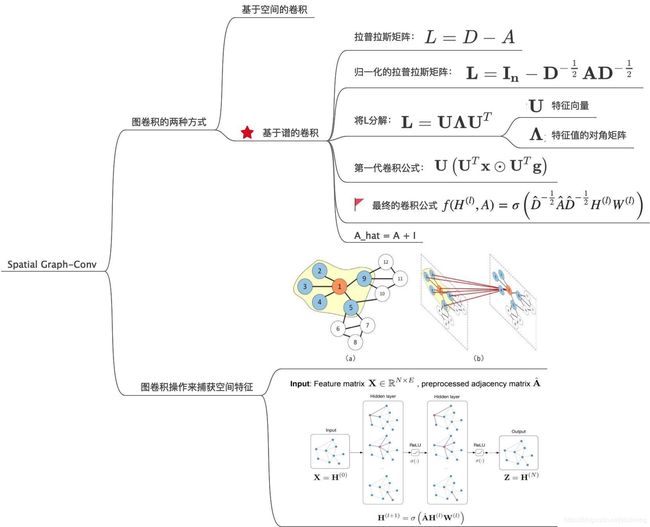
2.4：提取时间特征的门控卷积神经网络

提取空间特征的图卷积神经网络，即对应网络结构中的Temporal Gated-Conv 模块。

论文提到，每个ST—Conv模块包含两个时间门控卷积层和一个空间图卷积层。

在时间维度上，论文提到采用使用GLU实现的1维因果卷积，就不再像采用RNN的方法依赖于之前的输出，并且还可以对数据进行并行处理，这样使得模型训练速度更快。GLU是在这篇论文中提出的：Language Modeling with Gated Convolutional Networks。在STGCN这篇论文，文章只是简单提到采用这种操作可以缓解梯度消失等现象还可以保留模型的非线性能力。

在阅读论文源码后，我的理解是：采用GLU实现了在时间维度上的卷积操作，卷积核大小是13，即HW，H表示节点数量，W表示时间长度，因此在每个节点上使用GLU来捕获时间上的依赖关系，也就是利用GLU来实现TCN能够达到的效果——1D卷积和并行计算的功能

2.5：时空卷积块ST-Conv Block

将以上的图卷积和门控CNN组合成如图所示的结构，其中使用了瓶颈策略来实现尺度压缩和特征压缩。并在每层之后接归一化层来防止过拟合。
ST-Conv Block的公式就是图的另一个解释，输入数据先做时间维度卷积，输出结果再做图卷积，图卷积的输出结果经过一个RELU，在进行一个时间维度卷积，就是整个ST-Conv Block的输出。

2.6：模型输出

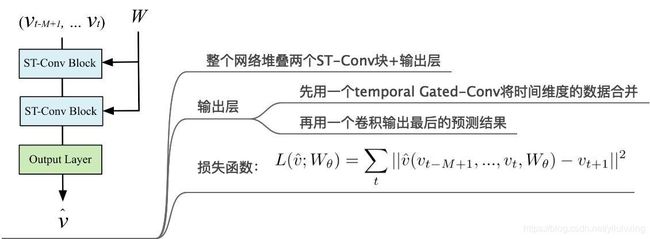
最后的模型是堆叠两个St-Conv Block之后接一个输出层，其中输出层首先用时间维度的卷积将之前的输出数据的时间维度进行合并，合并之后在经过一个卷积输出最终的预测数据，预测数据就是下一个时间维度的一张图[1,228,1]。模型采用的是L2损失。

2.7：模型总结

• STGCN 是处理结构化时间序列的通用框架。它不仅能够解决交通网络建模和预测问题，而且可以应用于更一般的时空序列学习任务。
• 时空卷积块结合了图卷积和门控时间卷积，能够提取出最有用的空间特征，并连贯地捕捉到最基本的时间特征。
• 该模型完全由卷积结构组成，在输入端实现并行化，参数更少，训练速度更 快。更重要的是，这种经济架构允许模型以更高的效率处理大规模网络。

3：源码解读

源码以Pytorch为例

3.1:读取数据

原始数据时间窗口长度是5min一个数据片，即：每5分钟记录该时间窗口内，各个路网节点的数据信息，每条数据信息包含2个维度信息。

utlis.load_metr_la_data函数

读取数据，并且利用 Z-score method进行归一化：
X = X - means.reshape(1, -1, 1)和 X = X / stds.reshape(1, -1, 1)，最终返回数据格式为：X:[207, 2, 34272]，表示有图中有207个节点，34272个时间片，每个时间片对应的节点数据维度是2

def load_metr_la_data():
    if (not os.path.isfile("data/adj_mat.npy")
            or not os.path.isfile("data/node_values.npy")):
        with zipfile.ZipFile("data/METR-LA.zip", 'r') as zip_ref:
            zip_ref.extractall("data/")

    A = np.load("data/adj_mat.npy")
    X = np.load("data/node_values.npy").transpose((1, 2, 0))
    X = X.astype(np.float32)

    # Normalization using Z-score method
    means = np.mean(X, axis=(0, 2))
    X = X - means.reshape(1, -1, 1)
    stds = np.std(X, axis=(0, 2))
    X = X / stds.reshape(1, -1, 1)

    return A, X, means, stds

utlis.get_normalized_adj函数

读取邻接矩阵，并返回度信息

def get_normalized_adj(A):
    """
    Returns the degree normalized adjacency matrix.
    """
    A = A + np.diag(np.ones(A.shape[0], dtype=np.float32))
    D = np.array(np.sum(A, axis=1)).reshape((-1,))
    D[D <= 10e-5] = 10e-5    # Prevent infs
    diag = np.reciprocal(np.sqrt(D))
    A_wave = np.multiply(np.multiply(diag.reshape((-1, 1)), A),
                         diag.reshape((1, -1)))
    return A_wave

utlis.generate_dataset函数

• 历史时间窗口长度：num_timesteps_input = 12，预测未来时间窗口长度：num_timesteps_output = 3，即用过去12个时间片信息，来预测接下来3个时间片的数值。
• 在main函数中，训练数据集为60%，即训练数量共34272*0.6=20563。main函数调用generate_dataseth函数，其原始输入为 (num_vertices, num_features,num_timesteps)，即 (207, 2, 20563)，207是节点数量，2表示每个时间片对应的特征数量，训练时间片数量为20563。
• 最后generate_dataseth返回X的结果为：(num_samples, num_vertices, num_features, num_timesteps_input)，即[20549, 207, 12, 2]，20549表示处理后的时间片数量，207表示节点数量，12表示特征数量也就是过去12个时间片，2表示特征的通道数量，generate_dataseth返回Y的结果为：(num_samples, num_vertices, num_features, num_timesteps_output)，即[20549, 207, 2]，其中的第一个通道的数值表示预测数值对应的通道。

def generate_dataset(X, num_timesteps_input, num_timesteps_output):
    """
    Takes node features for the graph and divides them into multiple samples
    along the time-axis by sliding a window of size (num_timesteps_input+
    num_timesteps_output) across it in steps of 1.
    :param X: Node features of shape (num_vertices, num_features,
    num_timesteps)
    :return:
        - Node features divided into multiple samples. Shape is
          (num_samples, num_vertices, num_features, num_timesteps_input).
        - Node targets for the samples. Shape is
          (num_samples, num_vertices, num_features, num_timesteps_output).
    """
    # Generate the beginning index and the ending index of a sample, which
    # contains (num_points_for_training + num_points_for_predicting) points
    indices = [(i, i + (num_timesteps_input + num_timesteps_output)) for i
               in range(X.shape[2] - (
                num_timesteps_input + num_timesteps_output) + 1)]

    # Save samples
    features, target = [], []
    for i, j in indices:
        features.append(
            X[:, :, i: i + num_timesteps_input].transpose(
                (0, 2, 1)))
        target.append(X[:, 0, i + num_timesteps_input: j])

    return torch.from_numpy(np.array(features)), \
           torch.from_numpy(np.array(target))

3.2：模型输入

这里batch_size设置为50，同时为了比较快速清晰的查看各个模块的输出，我们就以一个batch为例，即：输入的总时间片长度为50
STGCN包含三个模型，其中两个时空STGCNBlock模块和一个TimeBlock模块和最后一个全连接层，而一个STGCNBlock又包含两个temporal（temporal）模块，（也就是TimeBlock模块模块）和 一个Theta（spatial）模块，一个TimeBlock模块包含因果卷积操作目的就是为了提取时间信息(主要是W维度上的)TimeBlock模块主要是为了提取时间信息，利用的是一维卷积，kernel_size=3，卷积核大小为（1，kernel_size=3，分别对应H,W）。

• GLU操作：Theta（spatial）模块中的切比雪夫近似与一阶近似后的图卷积与上一个TimeBlock进行矩阵相乘计算，GLU单元来缓解梯度消失等现象还可以保留模型的非线性能力。
• TimeBlock模块的原始输入为：[50, 207, 12, 2]即[B,H,W,C]，经过尺度变换转换为pytorch最终的输入为[50, 2, 207, 12]，即[B,C,H,W]，尺度变换的原因在于要与卷积核对应，因为
  卷积核大小为（1，kernel_size=3，分别对应H,W)，调用一次TimeBlock模块H不变也就是207数值不变，W减小2,也就是12-2，即提取一个时间切片下的时间信息。
• STGCN包含三个模型，其中两个时空STGCNBlock模块(分别为block1和block2)和一个TimeBlock模块(last_temporal),block1和block2均包含2个TimeBlock,每个TimeBlock计算后,W要减少2，因此，两个block1和block2后，W共减少8，因此block2的输出结果为[50, 207, 4, 64]。
• 再利用切比雪夫近似与一阶近似后的图卷积公式进行计算，从而提取空间信息，STGCN中最后包含的TimeBlock模块主要是为了维度信息的缩放，输出通道统一为64，这样保证后面全连接的时候，
• 参数一致，如原始batch输入为[50, 207, 12, 2]，在经过整个STGCN的前两个时空STGCNBlock模块后，其输出大小为out3：[50, 207, 2, 64]，在经过最后一层的全连接之前，要进行维度调整，(out3.shape[0], out3.shape[1], -1)返回的是[50, 207, 3]。
• 最后再经过一个全连接层:self.fully = nn.Linear((num_timesteps_input - 2 * 5) *64,num_timesteps_output)返回预测的3个时间片结果

3.3：模型总结

• 数据导入和划分：
  数据导入后的格式为X:[207, 2, 34272]，60%用作训练集，数量共34272*0.6=20563，num_timesteps_input = 12，num_timesteps_output = 3，数据集生成函数返回的X结果为[20549, 207, 12, 2]。Y结果为[20549, 207, 3]，batch设置的数值为50，也就是每50个时间片数据进行训练。因此TimeBlock模块的输入为[50, 207, 12, 2]即[B,H,W,C]。
• 维度变换：
  STGCN = block1+block2+last_temporal：
  第一个Block中的第一个TimeBlock模块的定义为self.temporal1TimeBlock(in_channels=in_channels,out_channels=out_channels)，TimeBlock输入为[50, 207, 12, 2]即[B,H,W,C]，但需要进一步转换，转换后的结果为[50, 2, 207, 12]，即[B,C,H,W]，因为一般情况下，图网络数据转换为网格数据时，H一般表示网格节点数量，W表示特征数量（时空数据下的同一时间片的历史数据量），另一个尺度变换的原因在于要与卷积核对应，因为卷积核大小为（1，kernel_size=3，分别对应H,W)，C表示通道，B表示batch的大小，如果保持原始的[B,H,W,C]，则一维卷积则对W,C进行卷积，显然是不合理的。
• TimeBlock计算的结果是[50, 64, 207, 10]，即[B,C,H,W]（以调用一次TimeBlock为例，W减少2），再进行一次维度变换，返回的结果是[50, 207, 10, 64],即[B,H,W,C],因为后面还会调用TimeBlock，所以与上一次输入格式保持一致。
• GLU的定义为：self.Theta1 = nn.Parameter(torch.FloatTensor(out_channels,spatial_channels) — spatial_channels=16
  经过矩阵相乘，GLU的操作转换输出结果为[50, 207, 10, 16]，作为下一个TimeBlock的输入。
• 第一个block1中的第二个TimeBlock模块的定义为self.temporal2=self.temporal2 = TimeBlock(in_channels=spatial_channels,out_channels=out_channels)与第一个TimeBlock模块输出结果类似，self.tempora2的输出结果为[50, 207, 8, 64]，即self.temporal => self.Theta1 => self.tempora2 ,通道数量从64 => 16 => 64，也就是说self.Theta1模块经过一次非线性变换，只需要将输入，输出通道数量对齐即可。最后经过一层BN：self.tempora2的输出结果为[50, 207, 8, 64]，经过BN其输出维度保持不变：[50, 207, 8, 64]同理，再经过第二个block2后，BN层的输出结果为[50, 207, 4, 64]，最后一个last_temporal(TimeBlock)：其输入为[50, 207, 4, 64]，输出为[50, 207, 2, 64]
• 最后全连接层：self.fully = nn.Linear((num_timesteps_input - 2 * 5) *64,num_timesteps_output)，out4 = self.fully(out3.reshape((out3.shape[0], out3.shape[1], -1)))，输出结果为[50, 207, 3]

TimeBlock模块：

class TimeBlock(nn.Module):
    """
    Neural network block that applies a temporal convolution to each node of
    a graph in isolation.
    """

    def __init__(self, in_channels, out_channels, kernel_size=3):
        """
        :param in_channels: Number of input features at each node in each time
        step.
        :param out_channels: Desired number of output channels at each node in
        each time step.
        :param kernel_size: Size of the 1D temporal kernel.
        """
        super(TimeBlock, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, (1, kernel_size))
        self.conv2 = nn.Conv2d(in_channels, out_channels, (1, kernel_size))
        self.conv3 = nn.Conv2d(in_channels, out_channels, (1, kernel_size))

    def forward(self, X):
        """
        :param X: Input data of shape (batch_size, num_nodes, num_timesteps,
        num_features=in_channels)
        :return: Output data of shape (batch_size, num_nodes,
        num_timesteps_out, num_features_out=out_channels)
        """
        # Convert into NCHW format for pytorch to perform convolutions.
        X = X.permute(0, 3, 1, 2)
        temp = self.conv1(X) + torch.sigmoid(self.conv2(X))
        out = F.relu(temp + self.conv3(X))
        # Convert back from NCHW to NHWC
        out = out.permute(0, 2, 3, 1)
        return out

STGCNBlock模块

class STGCNBlock(nn.Module):
    """
    Neural network block that applies a temporal convolution on each node in
    isolation, followed by a graph convolution, followed by another temporal
    convolution on each node.
    """

    def __init__(self, in_channels, spatial_channels, out_channels,
                 num_nodes):
        """
        :param in_channels: Number of input features at each node in each time
        step.
        :param spatial_channels: Number of output channels of the graph
        convolutional, spatial sub-block.
        :param out_channels: Desired number of output features at each node in
        each time step.
        :param num_nodes: Number of nodes in the graph.
        """
        super(STGCNBlock, self).__init__()
        self.temporal1 = TimeBlock(in_channels=in_channels,
                                   out_channels=out_channels)
        self.Theta1 = nn.Parameter(torch.FloatTensor(out_channels,
                                                     spatial_channels))
        self.temporal2 = TimeBlock(in_channels=spatial_channels,
                                   out_channels=out_channels)
        self.batch_norm = nn.BatchNorm2d(num_nodes)
        self.reset_parameters()

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.Theta1.shape[1])
        self.Theta1.data.uniform_(-stdv, stdv)

    def forward(self, X, A_hat):
        """
        :param X: Input data of shape (batch_size, num_nodes, num_timesteps,
        num_features=in_channels).
        :param A_hat: Normalized adjacency matrix.
        :return: Output data of shape (batch_size, num_nodes,
        num_timesteps_out, num_features=out_channels).
        """
        t = self.temporal1(X)
        lfs = torch.einsum("ij,jklm->kilm", [A_hat, t.permute(1, 0, 2, 3)])
        # t2 = F.relu(torch.einsum("ijkl,lp->ijkp", [lfs, self.Theta1]))
        t2 = F.relu(torch.matmul(lfs, self.Theta1))
        t3 = self.temporal2(t2)
        return self.batch_norm(t3)
        # return t3

STGCN模块：

class STGCN(nn.Module):
    """
    Spatio-temporal graph convolutional network as described in
    https://arxiv.org/abs/1709.04875v3 by Yu et al.
    Input should have shape (batch_size, num_nodes, num_input_time_steps,
    num_features).
    """

    def __init__(self, num_nodes, num_features, num_timesteps_input,
                 num_timesteps_output):
        """
        :param num_nodes: Number of nodes in the graph.
        :param num_features: Number of features at each node in each time step.
        :param num_timesteps_input: Number of past time steps fed into the
        network.
        :param num_timesteps_output: Desired number of future time steps
        output by the network.
        """
        super(STGCN, self).__init__()
        self.block1 = STGCNBlock(in_channels=num_features, out_channels=64,
                                 spatial_channels=16, num_nodes=num_nodes)
        self.block2 = STGCNBlock(in_channels=64, out_channels=64,
                                 spatial_channels=16, num_nodes=num_nodes)
        self.last_temporal = TimeBlock(in_channels=64, out_channels=64)
        self.fully = nn.Linear((num_timesteps_input - 2 * 5) * 64,
                               num_timesteps_output)

    def forward(self, A_hat, X):
        """
        :param X: Input data of shape (batch_size, num_nodes, num_timesteps,
        num_features=in_channels).
        :param A_hat: Normalized adjacency matrix.
        """
        out1 = self.block1(X, A_hat)
        out2 = self.block2(out1, A_hat)
        out3 = self.last_temporal(out2)
        out4 = self.fully(out3.reshape((out3.shape[0], out3.shape[1], -1)))
        return out4