前言
这篇笔记是StatQuest系列视频教程的第36节,主要内容是有关FDR的。
什么是FDR
FDR的全称是false discovery rates。我们在做高通量测序的时候,或许听说过这个术语,但是FDR是如何来的呢,它是如何计算的呢,如下所示:
在讨论FDR的原理之前,我们就以大白话的形式来说一下FDR,FDR就是一种工具,它用来发现那些看起来貌似比较好的数据,如下所示:
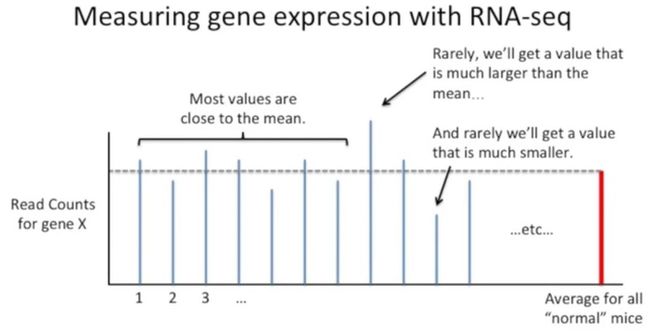
现在我们看一个案例,在下面的图形中,x轴是样本分组,y轴是基因x的Reads数,如下所示:
同理,RNA-seq并非完美无缺,每次测序,总会出现一定的偏差,如下所示:
当我们测序了许多次后,把它们放到一个坐标中,我们可以发现,它们都比较接近于平均水平,如下所示:
但是,在个别情况下,样本的数据会高于均值很多,或者是低于均值很多,如下所示:
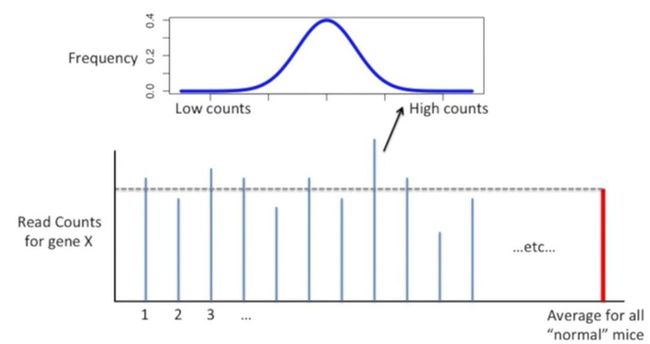
我们可以把这些数据放到正态分布曲线中,其中大多数都位于中间区域,如下所示:
而那些数据比较大的值可能位于曲线的右侧,如下所示:
数据量比较低的可能位于最左侧,如下所示:
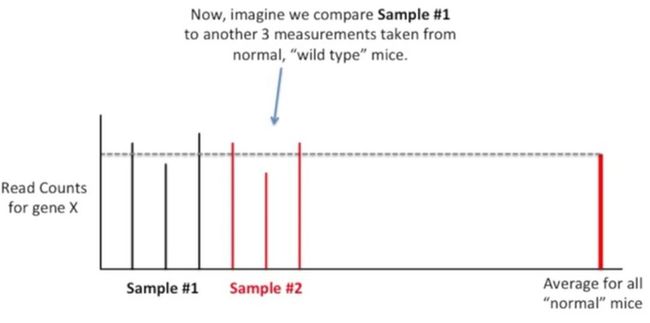
假如我们做了3只小鼠的测序,把这3只小鼠当作是样本1(Sample #1),如下所示:
那么样本1在多数情况下,都位于正态分布的中间区域,如下所示:
此时,我们将样本1与来源于另外3只正常的“野生型”小鼠进行比较,就是下面红线表示的3只小鼠(称为样本2),如下所示:
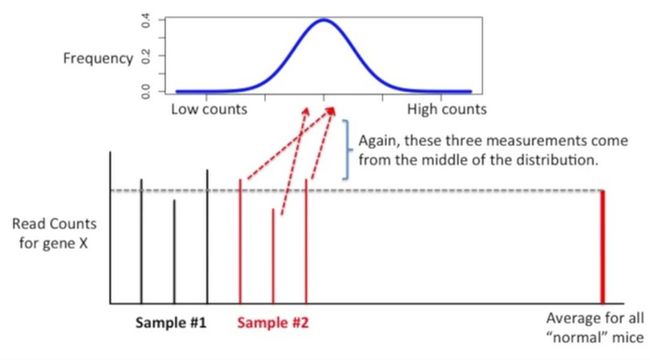
样本2的小鼠也基本上位于正态分布曲线的中间区域,如下所示:
如果我们对样本1和样本2做个t检验,那么有很大的可能是它们的p值很大,因为样本1和样本2有部分重合,如下所示:
但是,在个别情况下,这两个样本做2个t检验,p值有可能很小,小于0.05,此时这种现象就被称为“假阳性”,因为一个小的p值预示着这两个样本来源于2种不同品系的小鼠(也就是说来源于两个不同的分布),但实际上这两个样本是来源一个相同的分布,因此得到的结论是假的,如下所示:
通常来讲,假阳性这种情况很少,除非你被p值挟持(后文会提到)了,如下所示:
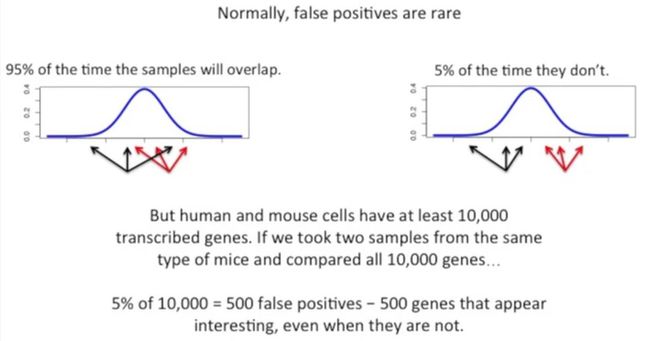
95%的情况下,源于同一个分布的不同的样本会出现重合,但在5%的情况下,样本并不重合,但是,人和小鼠细胞有至少10000个转录的基因,如果是来源于相同小鼠的2个样本,然后我们比较这所有的10000个基因的话,可能有500个假阳性结果,这就比较尴尬了,如下所示:
500个假阳性结果不是一个小数字,如何解决这个问题?如下所示:
FDR的基本思想
FDR就能控制假阳性结果的数目,从技术层面来讲,FDR并不是一种具体的限制假阳性结果的方法,很多种算法都可以计算FDR,常用的就是Benjamini-Hochberg法。在我们讲这个方法之前,我们来看一下这个方法的基本思想是什么,如下所示:
同一分布的p值计算
此时我们先从同一个分布中,随机生成10000对样本(样本1和样本2),然后计算这10000个p值,如下所示:
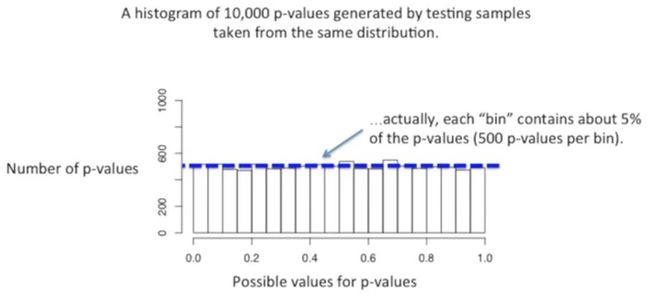
然后将这些p值绘制成直方图,其中横坐标是p值的大小,如下所示:
纵坐标是p值的数目,如下所示:
我们看直方图的第1列,也就是下图红色的部分,有510个p值(5.1%)小于0.05,如下所示:
再看第2列,有差不多数目的p值大于0.05,小于0.1,如下所示:
事实上,每1列的数目基本上都接近于500(也就是5%的总体数目),如下所示:
由于p值的分布都比较均匀,因此在这10000个样本对(样本1和样本2)中,检验结果得到的p值落到每个区间的可能性基本上都是一样的,如下所示:
不同分布样本的p值
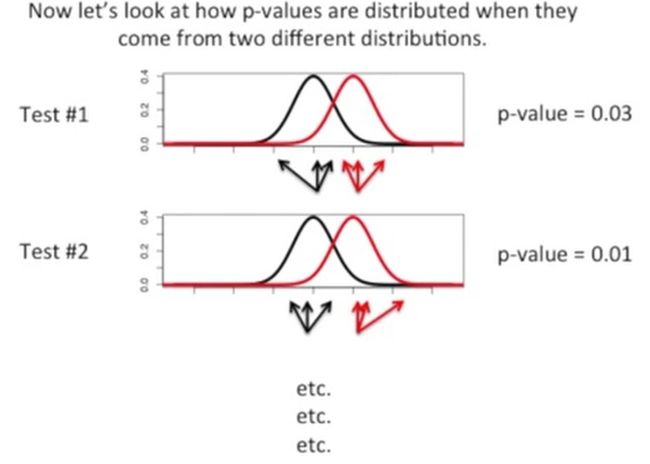
前面讲的是,10000个来源于相同分布的样本对(样本1和样本2),此时我们研究一下,如果这两个样本来源于不同的分布是什么情况,如下所示:
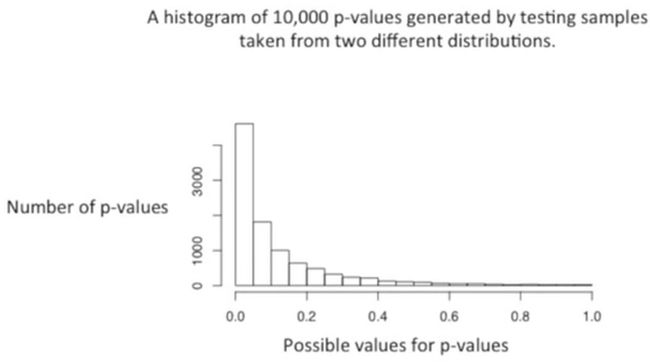
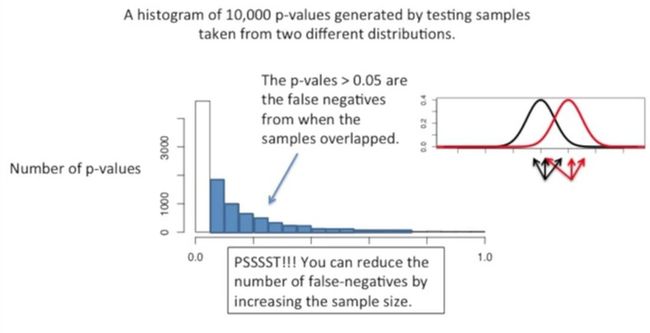
然后我们将这10000个p值绘制成直方图,如下所示:
其中大部分的p值都是小于0.05的,如下所示:
其中p值大于0.05的是假阳性的数目,如下所示:
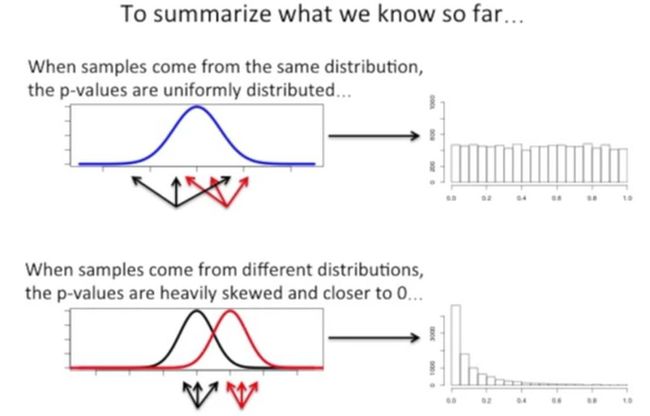
现在总结一下这两个案例:
第一,如果样本来源于同一个分布,那么p值分布比较均值;
第二,如果样本是来源于不同的分布,那么p值的分布就不太均值,它们主要偏向于0,如下所示:
生物学案例
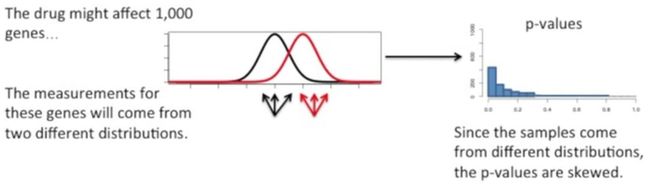
此时,我们来看一个生物学方面的案例,在这个案例中,我们用某个药物处理神经细胞,如下所示:
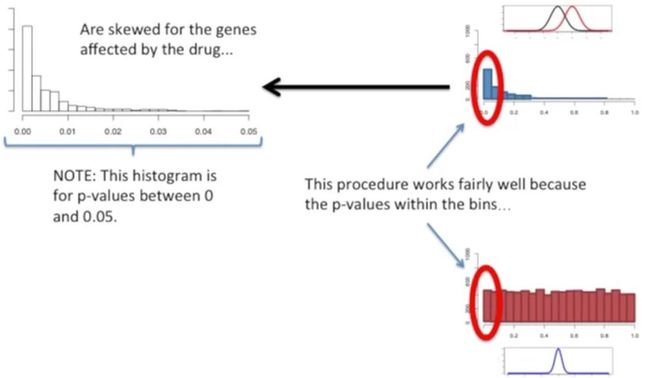
这个药物或许能够影响1000个基因,然后我们可以认为对照组与实验组各自的1000个基因来源于两个不同的分布,其中黑色的表示对照组,红色表示实验组,由于这两个分布不同,那么来源于这两个样本的统计结果的p值直方图会偏向于0,如下所示:
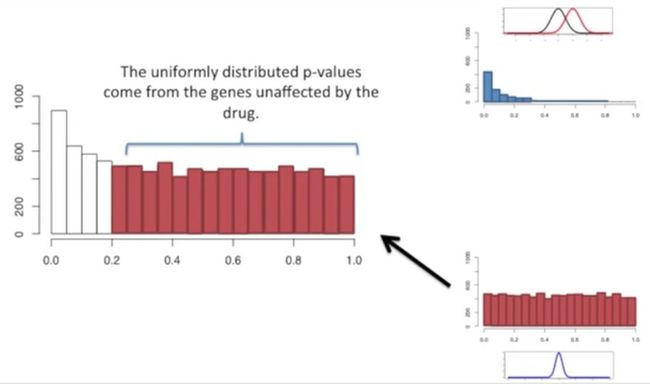
而剩余的9000个基因(前面我们提到过动物细胞转录的基因至少有10000个)可许并不受这个药物的影响,这就意味着,对照组与实验中的各自的9000个基因来源于相同的分布,那么它们的p值分布就比较均匀了,如下所示:
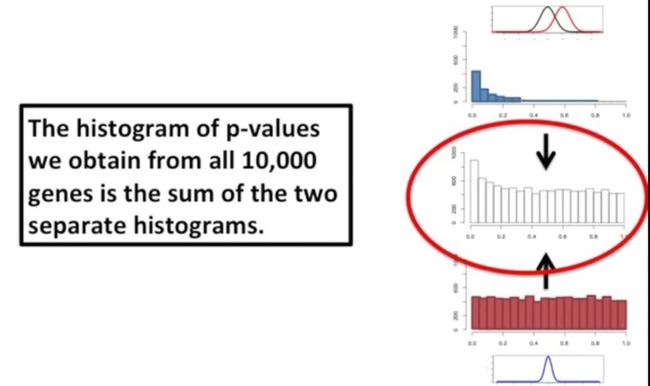
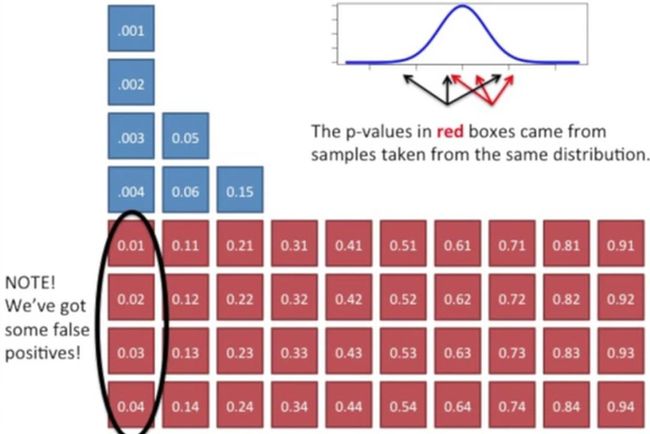
那么,最终我们检测的实验组与对照组的这所有的10000个基因就是来源于不同分布的1000个基因与来源于相同分布的9000个基因的总和,如下所示:
来源于相同分布的基因的p值并不受药物影响,如下所示:
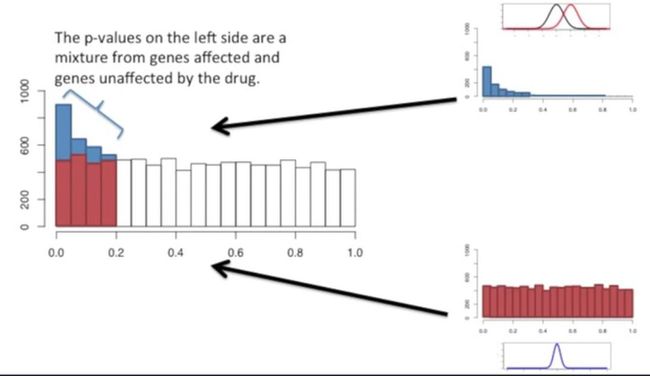
而左侧直方图的区间则是混合了那些药物影响的基因和不影响的基因,如下所示:
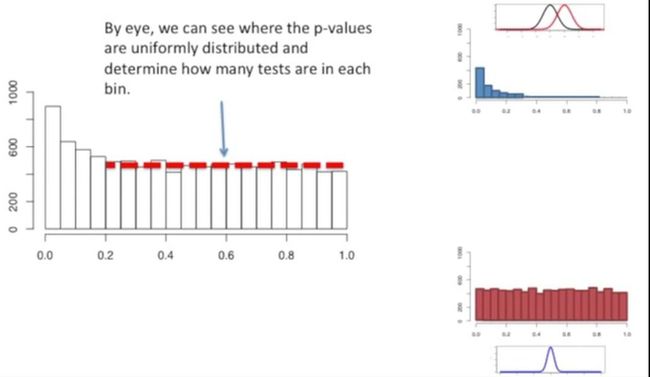
仅凭肉眼观察,我们就可以大概看到哪些p值是均匀分布的,以前它们所做的检验数目,如下所示:
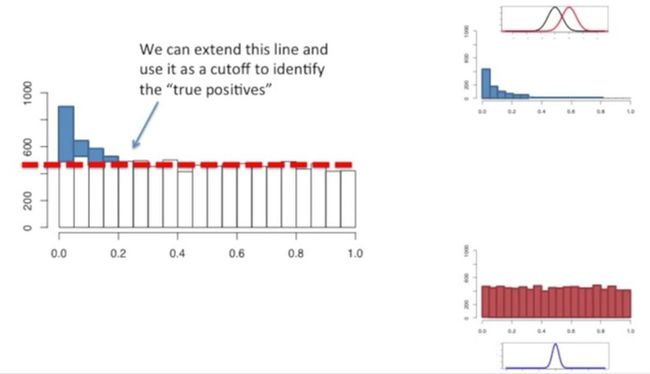
我们把这条红线延伸,把它作为一个阈值,从而找到“真阳性”,如下所示:
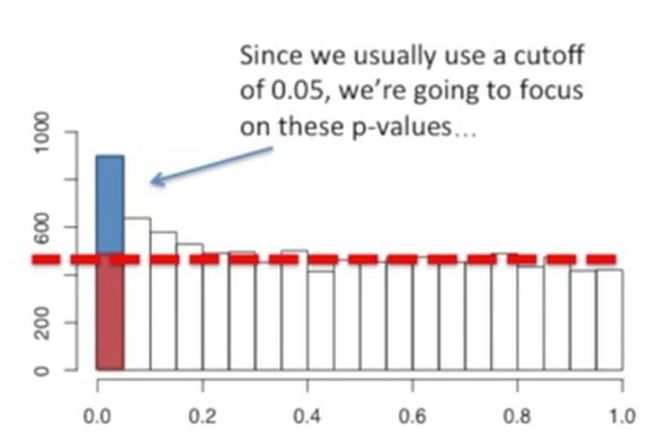
我们使用的p值的阈值通常是0.05,此时我们主要看这些p值(蓝色部分),如下所示:
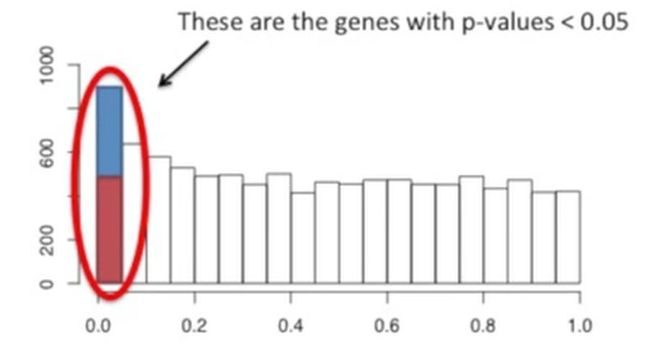
其中我们可以发现,红色虚线以上的p值小于0.05的数目大概是450个,以下的数目上大概也是450个,如下所示:
一种从假阳性中分离真阳性的途径就是只考虑最小的450个p值(我的理解就是只考虑最左侧的那个区间),如下所示:
这种方法计算的结果通常不错,因为大多数都位于这个区间p值都是那些基因受到药物影响的基因,如下所示:
那些不受药物影响的基因p值通常都是均值分布的,将它们接近的均值(就是前面的红色虚线)平稳地延伸,就可以计算出真阳性,如下所示:
BH法
BH法简介
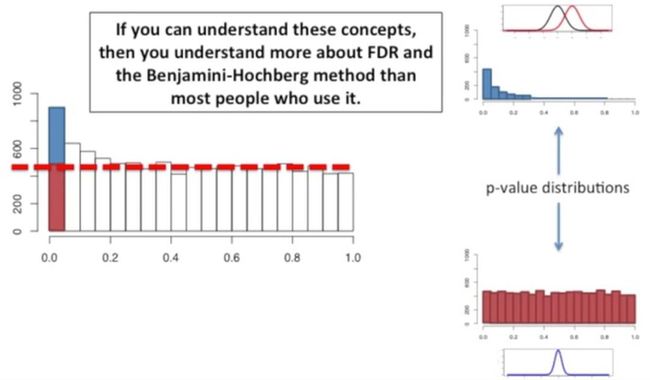
如果你理解了上述的一些基本思想,那么此时我们来看一下FDR更多的细节与Benjamini-Hochberg法(简称BH法),如下所示:
BH法是基于“肉眼法”(eyeball)(也就是我们用肉眼来观察),这种方法能够校正p值,从而限制那些所谓的有显著差异的p值的假阳性数目,校正的p值会让p值变得更大,例如在进行FDR校正之前,你的p值是0.05(有显著性),经过FDR校正,p值有可能变成0.06了(不再有显著性),如下所示:
如果你选择的阈值是FDR<0.05,然后在那些“显著性”结果中,有大概不到5%的结果会成为假阳性,如下所示:
在下图中,这些基因的统计结果p值是小于0.05的,如下所示:
下面是那些经过FDR校正后的p值小于0.05的数目,我们需要注意的是,并非所有的“真阳性”基因都位于这个方框中,并且,在这个方框中,只有5%的经过校正的p值是假性,剩余的95%是真阳性,如下所示:
此时有一个疑问,为什么并非所有的真阳性基因的校正p值都小于0.05?因此并非所有的真阳性基因都有一个非常小的p值,在下图的左下角是p值小于0.05的真阳性基因的直方图,在直方图的右侧,有一部分基因经过校正后,它们的p值不再有显著性,如下所示:
BH法的数学原理
BH法背后的数学原理比较简单,我们先看一个简单的案例。
假如有10对样本(样本1和样本2)来源于同一个分布(例如前面不受药物影响的10个基因),我计算一下它们的p值,如下所示:
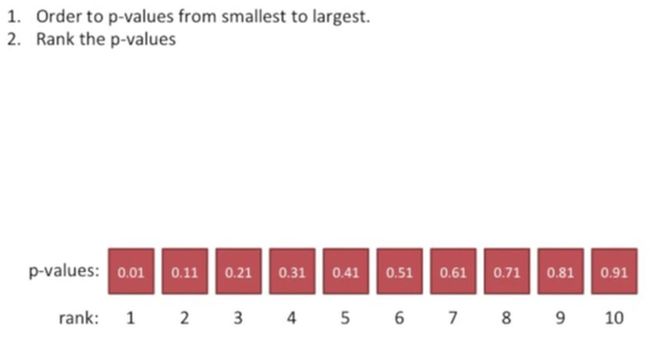
此时,我们把p值从小到大排列,最小的p值是0.01,它明显是一个假阳性,此时我们看一下BH法是如何处理这种情况,如下所示:
此时我们对这10个p值进行编号,分别编号为1到10,如下所示:
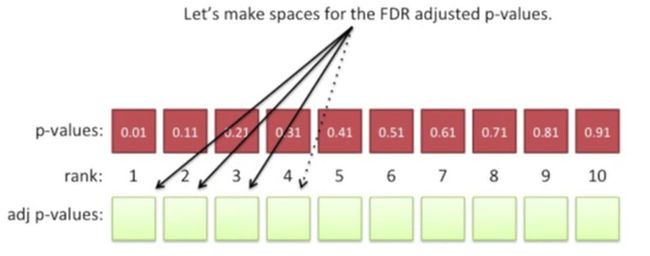
现在给这些p值校正的结果留下相应的位置,如下所示:
经校正后,我们把校正后的最大的p值放到第10个新位置,通常还是原来最大的p值,如下所示:
接着,我们在第9个位置放校正后的次大的p值(也就是第二大的p值),关于这个p值如何校正呢,它需要2个参数,第1个参数就是总的p值数目,在这个案例中,总的p值数目是10,第二个参数是要校正的p值的秩(也就是这个p值在这10个p值中按从小到大排列,它排第几),在这个案例中,0.81这个p值的秩是9,那么校正的公式就是总的p值数目除以要校正的p值的秩,然后再乘以这个p值的大小,如下所示:
经计算,p值为0.81,校正后的结果为0.9,计算过程如下所示:
此时再看第8个位置的校正p值,还按上面的公式进行计算,p值为0.71,经校正后就是0.89,如下所示:
所有的p值都按此方法进行校正,结果如下所示:
从上面的结果来看,原来是0.01的这个p值经校正后,它的p值是0.中,原来是阳性,现在就不是阳性了,不再具备显著性。
一个复杂案例
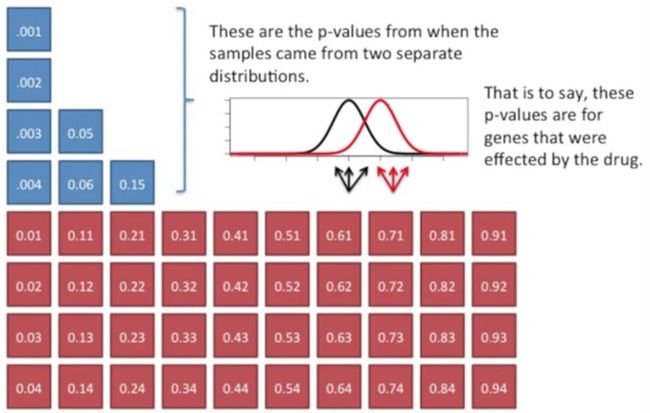
此时,我们再看一个比较复杂的案例,如下所示:
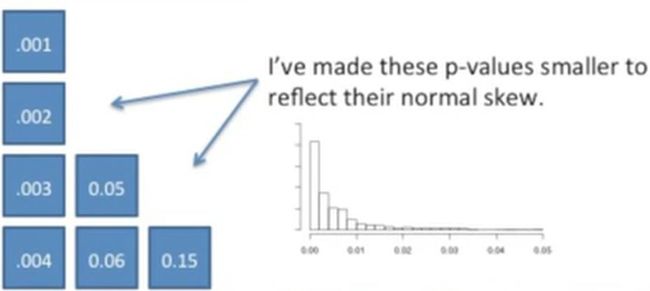
其中蓝色部分有可能来源于不同的分布(因为它们的p值小于0.05),也就是说,来源于那些能够被药物影响的基因,而红色的部分有可能是来源于相同的分布(因为它们的p值多数都大于0.05),也就是说,红色的来源于那些无法被药物影响的基因,如下所示:
此时绘制蓝色样本的正方图,如下所示:
红色是来源于相同的分布,但我们从中可以发现,它里面有几个假阳性,如下所示:
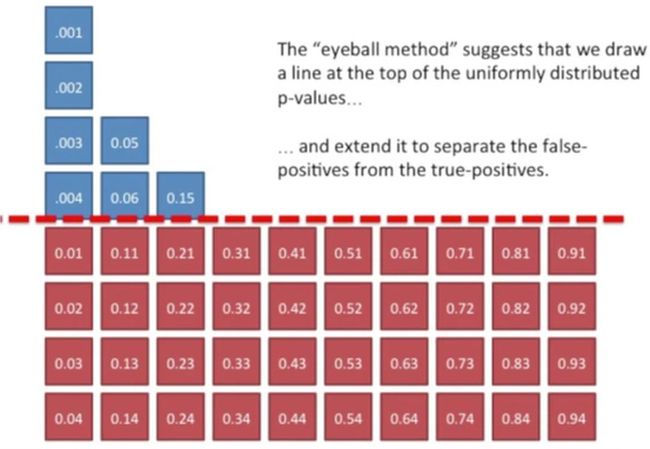
通过肉眼法(eyeball method),我们绘制一条这些分布的虚线,并把这些虚线延伸到最左侧,找到真阳性的结果,如下所示:
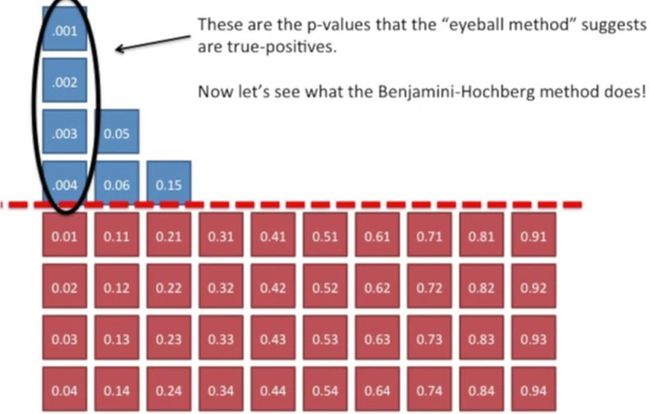
红色虚线以上的部分就是我们利用“肉眼”法找到的真阳性结果,此时我们看一下如何通过BH来找真阳性,如下所示:
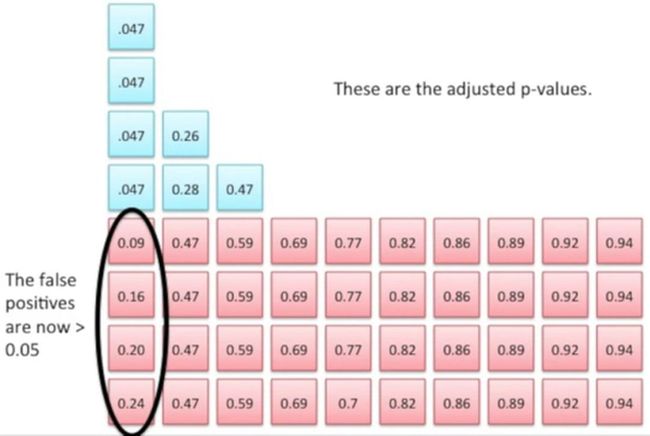
通过前面我们提到的方法对这些p值进行校正,校正后的结果如下所示:
我们可以发现,那些假阳性的p值经校正后,它们都大于0.05了,如下所示:
但真阳性的p值还在0.05以下,如下所示: