【数论推导】Educational Codeforces Round 106 Problem D: The Number of Pairs

D-The Number of Pairs

传送门

题目大意：
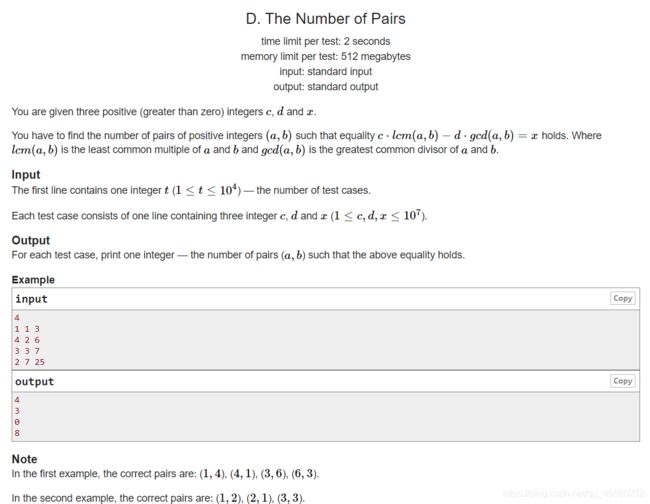
给定 $c,d,x$, 找出有多少对正整数对 $(a,b)$ 满足下述等式：
$$c•lcm(a,b)-d•gcd(a,b)=x$$
解题思路:
$$\begin{gathered} c•lcm(a,b)-d•gcd(a,b)=x; \\ lcm(a,b)=\frac{a•b}{gcd(a,b)}; \\ \frac{c•a•b}{gcd(a,b)}-d•gcd(a,b)=x; \end{gathered}$$
令$g=gcd(a,b)$,则有$a=k_1•g$, $b=k_2•g$；
$$\begin{gathered} c•k_1•k_2•g-d•g=x; \\ g•(c•k_1•k_2-d)=x; \\ g=\frac{x}{c•k_1•k_2-d}; \end{gathered}$$
其中$g\in N^{+}$,即$(c•k_1•k_2-d)|x;$ (符号解释：$x|y$ 指的是 $x$ 可以整除 $y$,即 $y$ % $x==0$)
由此可以想到枚举 $x$ 的约数来求解;假设其中的一个约数为 $y$;
$$\begin{gathered} y=c•k_1•k_2-d; \\ {k}_1•k_2=\frac{y+d}{c}; \end{gathered}$$
在约数 $y$ 确定的情况下,$g$的值也是确定的，因$a=k_1•g$, $b=k_2•g$,所以$k_1$ 与 $k_2$ 的值和$a与b$的值是一 一对应的,因此可通过计算$(k_1,k_2)$的对数来间接计算$(a,b)$的对数。
$gcd(a,b)=g$, $k_1$与$k_2$互质。令 $m=\frac{y+d}{c}$ ;
问题： 需要求有多少对互质的正整数的乘积是$m$？
算术基本定理：任何一个大于1的自然数 $N$, 如果 $N$ 不为质数，那么$N$ 可以唯一分解成有限个质数的乘积。
则 $m$ 可以表示为:$m=p_1^{c_1}•p_2^{c_2}•...•p_n^{c_n}$
任意两个质数之间是互质的，$1$与任意的正整数都是互质的。
很明显相同的质因子不能同时出现在 $k_1$ 和 $k_2$ 中,则可按照质因数种类数将其化分为 $n$ 类,对于每一类数要么全部放入$k_1$中，要么全部放入$k_2$中。因质数之间互质，固质数的幂之间同样是互质的，所以以这种形式划分是合理的。每一类都有两种选择，一共有$n$类，所以总的方案数为$2^n$种。
综上所述，本题的答案即为：$answer=\sum _{y|x}get(y)$.
$get函数$：传入参数 $y$ ,计算出$\frac{y+d}{c}$的质因子个数$cnt$,返回$2^{cnt}$;
分析一下时间复杂度，线性筛O(n),枚举约数$\sqrt{n}$,t次询问，$get$函数O（$\sqrt{\frac{n}{logn}}$）,总的时间复杂度O($n+t$•$\sqrt{n}$•$\sqrt{\frac{n}{logn}}$),$t\in 1e4.n\in 1e7$,很明显时间复杂度很大。接下来考虑优化。
每一个数的质因子个数可以在线性筛中维护，具体维护方法请参考代码。因此get函数即可O(1)的时间复杂度来实现。
总的时间复杂度O($n+t•\sqrt{n}$)，大约是O(4e7),在2s的时间限制内完全可以过掉。

上代码：

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N = 20000010;
ll c, d, x;
ll prime[N], cnt;
ll vis[N];
void get_prime()
{
     
    for (int i = 2;i < N;i++)
    {
     
        if (!vis[i]) prime[cnt++] = i, vis[i] = 1;
        for (int j = 0;prime[j] <= N / i;j++)
        {
     

            if (i % prime[j] == 0)
            {
     
                vis[prime[j] * i] = vis[i];
                break;
            }
            else {
     
                vis[prime[j] * i] = vis[i] + 1;
            }
        }

    }
}
ll qpow(ll a, ll b)
{
     
    ll res = 1;
    while (b)
    {
     
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
    }
    return res;
}
ll get(ll i)
{
     
    if ((i + d) % c) return 0;
    int m = (i + d) / c;
    return qpow(2, vis[m]);
}
int main()
{
     
    int t;cin >> t;
    get_prime();
    while (t--)
    {
     
        cin >> c >> d >> x;
        ll ans = 0;
        for (int i = 1;i <= x / i;i++)
        {
     
            if (x % i == 0)
            {
     
                ans += get(i);
                if (x / i != i) ans += get(x / i);
            }
        }
        cout << ans << endl;
    }
    return 0;
}

参考文献