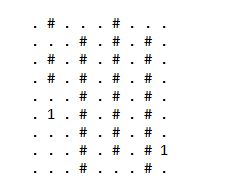【BFS】BFS系列模板

1.走迷宫

题目传送门

题目描述：

给定一个n*m的二维整数数组，用来表示一个迷宫，数组中只包含0或1，其中0表示可以走的路，1表示不可通过的墙壁。
最初，有一个人位于左上角(1, 1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问，该人从左上角移动至右下角(n, m)处，至少需要移动多少次。
数据保证(1, 1)处和(n, m)处的数字为0，且一定至少存在一条通路。

输入格式

第一行包含两个整数n和m。
接下来n行，每行包含m个整数（0或1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100

输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8

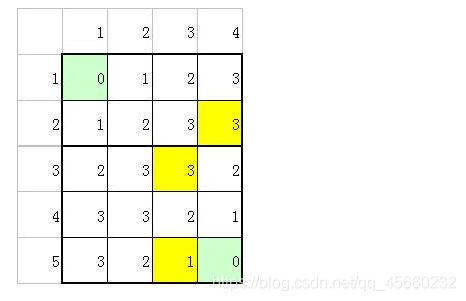
解题思路：用一个队列维护一个BFS搜索顺序，由近及远的进行搜索，搜出一条最短路，!注意！在用BFS解决最短路问题的时候，仅适用于所有边权都相等的情况

上代码：

#include
#include
#include
#include
using namespace std;
int n,m;
struct pos{
     
    int x,y;
}cnt1,cnt2,cnt3;
int a[110][110],d[110][110];
void bfs()
{
     
    queue<pos>q;
    int dx[]={
     0,1,0,-1};
    int dy[]={
     1,0,-1,0};
    d[1][1]=0;
    cnt1.x=1,cnt1.y=1;
    q.push(cnt1);
    while(!q.empty())
    {
     
        cnt2=q.front();
        q.pop();
        for(int i=0;i<4;i++)
        {
     
            int x=cnt2.x+dx[i],y=cnt2.y+dy[i];
            if(x>=1&&x<=n&&y>=1&&y<=m&&a[x][y]==0&&d[x][y]==-1)
            {
     
                d[x][y]=d[cnt2.x][cnt2.y]+1;
                cnt3.x=x;
                cnt3.y=y;
                q.push(cnt3);
            }
        }
    }
}
int main()
{
     
    cin>>n>>m;
    memset(d,-1,sizeof d);
    for(int i=1;i<=n;i++)
    {
     
        for(int j=1;j<=m;j++)
        {
     
            cin>>a[i][j];
        }
    }
    bfs();
    cout<<d[n][m]<<endl;
    return 0;
}

再来一道稍简单一点的题

2.UPC Contest2304 - 2020春季个人训练赛第八场（新生场）问题E–圣诞岛的走廊

题目描述

下了飞机，Angel走到了一个奇怪的走廊里。走廊非常的窄，只有2格宽，但是却很长。Angel想尽快走出这个走廊，你能帮他吗？
走廊有n(n<=10,000)行，但是只有2列。走廊中有一些格子不能被通过，从一个格子移动到上、下、左、右的相邻格子需要1单位时间。问Angel最少什么时候达到第n行？假设Angel一开始在左上角(第1行)。

输入

第一行n，然后n行，每行两个数字，0代表能通过，1代表不能通过。

输出

输出一行，代表最少需要的时间。
如果永远不能到达，输出一行Poor。

样例输入 Copy

5
0 0
1 0
0 0
0 1
0 0

样例输出 Copy

6

思路上一道题一个样，唯一多了一个就是需要判断一下是否能够到达目的地

上代码：

#include
using namespace std;
struct point{
     
	int x,y;
}node,tal,tes;
int n;
int vis[10010][3],a[10010][3],d[10010][3];
void bfs()
{
     
	int dx[]={
     -1,0,1,0};
	int dy[]={
     0,1,0,-1};
	queue<point>q;
	d[1][1]=0;
	tes.x=1,tes.y=1;
	q.push(tes);
	while(!q.empty())
	{
     
		tal = q.front();
		q.pop();
		for(int i=0;i<4;i++)
		{
     
			int x=tal.x+dx[i],y=tal.y+dy[i];
			if(x>=1&&x<=n&&y>=1&&y<=2&&a[x][y]==0&&d[x][y]==-1)
			{
     
				d[x][y]=d[tal.x][tal.y]+1;
				node.x=x,node.y=y;
				q.push(node);
			}
		}
	}
//	for(int i=1;i<=n;i++)
//	{
     
//		for(int j=1;j<=2;j++)
//		{
     
//			cout<
//		}
//		puts("");
//	}
	//return min(d[n][1],d[n][2]);
}
int main()
{
     
	int i,j;
	memset(d,-1,sizeof(d));//记录有没有走过 
	cin>>n;
	for(i=1;i<=n;i++)
	{
     
		for(j=1;j<=2;j++)
		{
     
			cin>>a[i][j];
		}
	}
	bfs();
	if(d[n][1]==-1&&d[n][2]==-1)
	{
     
		cout<<"Poor"<<endl;
	}
	else{
     
		if(d[n][1]==-1) cout<<d[n][2];
		else if(d[n][2]==-1) cout<<d[n][1]<<endl;
		else cout<<min(d[n][1],d[n][2]);
	}
	return 0;
}

3.八数码

AcWing 八数码
解题思路：维护每一个状态，每个状态用一个字符串表示，然后广搜每一个状态，有一个关键的地方就是状态转移，怎样把一个一维的数组中的坐标转化为二维中的坐标，还有就是怎么把二维数组中的坐标转化为一维的坐标，例如a [ k ]表示一维数组中的某个元素，然后将其转化为n行m列的二维数组的坐标时，对应的横纵坐标分别为 x = k / m , y = k % m ; 及对应坐标 b [ k / m ] [ k % m ] ;然后就是怎样把二维的转化为一维的，例如b [ x ] [ y ] 转化为一维的就是a [ m * x + y ];

上代码：

#include
#include
#include
#include
using namespace std;

int bfs(string start)
{
     
    int dx[]={
     0,-1,0,1},dy[]={
     1,0,-1,0};
    string ends="12345678x";
    queue<string> q;
    unordered_map<string,int> d;
    d[start]=0;
    q.push(start);
    while(!q.empty())
    {
     
        auto t=q.front(); q.pop();
        int distance=d[t];
        if(t==ends) return distance;
        int k=t.find('x');//返回x的下标
        int x=k/3,y=k%3;
        for(int i=0;i<4;i++)
        {
     
            int a=x+dx[i],b=y+dy[i];
            if(a>=0&&a<3&&b>=0&&b<3)
            {
     
                swap(t[k],t[3*a+b]);
                if(!d.count(t))//即判断d[t]是否为零
                {
     
                    d[t]=distance+1;
                    q.push(t);
                }
                swap(t[k],t[3*a+b]);
            }
        }
    }
    return -1;
}

int main()
{
     
    string start;
    for(int i=1;i<=9;i++)
    {
     
        string c;
        cin>>c;
        start+=c;
    }
    cout<<bfs(start)<<endl;
    return 0;
}

4.数字变换（BFS基础模板题）

题目描述

给定一个数N (O≤N≤100000)，变成另一个数K(O≤K≤100000)，允许的操作是乘以2，或者加减1，问最少要几步才能完成？

输入

仅有两个整数 N 和 K。

输出

一个整数，表示需要的最少步数。

样例输入
5 17
样例输出
4
解题思路：当n>=K的时候，直接输出n-k就是答案，因为变小的只有 -1 这一个操作，当n

上代码：

#include
#include
#include
#include
#include
using namespace std;
const int N = 100010;
typedef pair<int, int> PII;
bool vis[N];
int bfs(int n, int k)
{
     
    queue<PII> q;
    memset(vis, false, sizeof vis);
    vis[n] = true;
    q.push({
      n,0 });
    while (!q.empty())
    {
     
        auto item = q.front();
        q.pop();
        if (item.first == k)
        {
     
            return item.second;
        }
        if (item.first + 1 <= N && !vis[item.first + 1])
        {
     
            auto tmp = item;
            tmp.first += 1;
            tmp.second += 1;
            q.push(tmp);
            vis[tmp.first] = true;
        }
        if (item.first - 1 >=0 && !vis[item.first - 1])
        {
     
            auto tmp = item;
            tmp.first -= 1;
            tmp.second += 1;
            q.push(tmp);
            vis[tmp.first] = true;
        }
        if (item.first * 2 <= N && !vis[item.first * 2])
        {
     
            auto tmp = item;
            tmp.first *= 2;
            tmp.second += 1;
            q.push(tmp);
            vis[tmp.first] = true;
        }
    }
}
int main()
{
     
    int n, k;
    cin >> n >> k;
    if (n >= k) cout << n - k << endl;
    else cout << bfs(n, k) << endl;
    return 0;
}

5.UPC Contest2355 - 2020春季个人训练赛第二十五场 B:青铜莲花池

题目描述

为了让奶牛们娱乐和锻炼，农夫约翰建造了一个美丽的池塘。这个长方形的池子被分成了M行N列个方格（1 ≤ M, N ≤ 30）。一些格子是坚固得令人惊讶的莲花，还有一些格子是岩石，其余的只是美丽、纯净、湛蓝的水。
贝西正在练习芭蕾舞，她站在一朵莲花上，想跳到另一朵莲花上去，她只能从一朵莲花跳到另一朵莲花上，既不能跳到水里，也不能跳到岩石上。
贝西的舞步很像象棋中的马步：每次总是先横向移动M1 （1 ≤ M1 ≤ 30）格，再纵向移动M2 （1 ≤ M2 ≤ 30, M1 M2）格，或先纵向移动M1格，再横向移动M2格。最多时，贝西会有八个移动方向可供选择。
给定池塘的布局和贝西的跳跃长度，请计算贝西从起点出发，到达目的地的最小步数，我们保证输入数据中的目的地一定是可达的。

输入

第一行：四个用空格分开的整数：M，N，M1和M2
第二行到M + 1行：第i + 1行有N个用空格分开的整数，描述了池塘第i行的状态：0 为水，1 为莲花，2 为岩石，3 为贝西所在的起点，4 为贝西想去的终点。

输出

一个整数，表示从起点到终点的最少步数

样例输入
4 5 1 2
1 0 1 0 1
3 0 2 0 4
0 1 2 0 0
0 0 0 1 0

样例输出
2
提示

贝西从第二行的最左边出发，目标是第二行的最右边。贝西先跳到第一行第三列的莲花上，再跳到终点，需要两步。

这个题其实也算是模板题，唯一发生了点变化的就是搜索方向稍有变化，迷宫类的只是搜索上下左右四个方向，而对于这道题就产生了八个方向，所以需要对这八个方向都进行搜索，处理一下方向数组就行，不是太难搞；注意一点就是 每次总是先横向移动M1 （1 ≤ M1 ≤ 30）格，再纵向移动M2 （1 ≤ M2 ≤ 30, M1 M2）格这句活需要理解好，连续跳了两次是走了一步。其他的就是按照走迷宫的思路进行广搜就行，找一个d数组记录走的步数

上代码：

#include
#include
#include
#include
#include
#include
using namespace std;
typedef pair<int, int> PII;
int m, n, m1, m2;

int a[40][40], d[40][40];
bool vis[40][40];
int bfs(int t1, int t2)
{
     
	queue<PII> q;
	q.push({
      t1,t2 });
	int dir[8][2] = {
      m1,m2,m1,-m2,-m1,m2,-m1,-m2,m2,m1,m2,-m1,-m2,m1,-m2,-m1 };
	while (!q.empty())
	{
     
		auto t = q.front();q.pop();vis[t.first][t.second] = true;
		if (a[t.first][t.second] == 4) return d[t.first][t.second];
		int distance = d[t.first][t.second];
		for (int i = 0;i < 8;i++)
		{
     
			int x = t.first + dir[i][0], y = t.second + dir[i][1];
			//cout << dir[i][0] << " " << dir[i][1] << endl;
			if (x >= 1 && x <= m && y >= 1 && y <= n && !vis[x][y])
			{
     
				d[x][y] = distance + 1;
				q.push({
      x,y });
				vis[x][y] = true;
			}
		}
	}
	return -1;
}
int main()
{
     
	int cnt1=1, cnt2=1;
	memset(vis, false, sizeof vis);
	cin >> m >> n >> m1 >> m2;
	for (int i = 1;i <= m;i++)
	{
     
		for (int j = 1;j <= n;j++)
		{
     
			cin >> a[i][j];
			if (a[i][j] == 3) cnt1 = i, cnt2 = j;
			else if (a[i][j] == 0 || a[i][j] == 2) vis[i][j] = true;
		}
	}
	int ans = bfs(cnt1, cnt2);
	cout << ans << endl;
	return 0;
}

在BFS函数中，我给加上了一个return -1,这个是指搜不到的情况，但是题目给的数据都是保证一定能搜到的情况，所以这句号就显得可有可无啦，如果数据中再加上搜不到的情况，那这句活就有用了，暂且先加上也无妨

6.UPC Contest2388 - 2020年春混合个人训练第二场 F：解密码

题目描述
跑男们都被关进了瘦西湖风景区中的不同地点，天才陈赤赤被关在了白塔中。为了打开门上的密码锁，必须按照规则变换锁上的数字：开始给定一个4位的质数a，每次改变质数的一位（改变后仍为质数），用最少的次数改变后得到b，若不可能，则次数为0。
“论吃饭我一个人可以拼他们六个！”
“你是猪吗？”
“嗝~~~”
……
陈赤赤啰嗦了大半天也没有半点头绪，眼看天就黑了，作为黑衣人的你实在看不下去了，扔了一张小纸条给他。

输入
输入共一行，包含两个整数a,b。

输出
输出共一行，包含一个整数，表示最少的步数。

样例输入
1033 8179
样例输出
6
提示
1033->1733->3733->3739->3779->8779->8179
其中1033，1733，3733，3739，3779，8779，8179均为质数。

这道题和上述问题4是同一类型问题，都是求的由一个数字转换为另一个数字的最少操作次数，这道题相比于第4题稍难了一点，难点在于 素数筛的运用 和 数的转换过程，这个需要考虑拆分此四位数的每一位 对于每一位数由0- -9中的数字来替换，再判断是不是素数，如果是素数而后才能入队进入BFS搜索行列，其他的就是BFS的基本操作啦；

上代码：

#include
#include
#include
#include
using namespace std;
const int N = 10010;
typedef pair<int, int> PII;
bool vis[N],isprime[N];
int prime[N], s,b;
void get_prime() {
     
	for (int i = 2; i < N; i++) {
     
		if (!vis[i])
		{
     
			prime[s++] = i;
			isprime[i] = true;
		}	
		for (int j = 0; j < s && i * prime[j] < N; j++) {
     
			vis[i * prime[j]] = 1;
			if (i % prime[j] == 0) break;
		}
	}
}
int bfs(int a)
{
     
	queue<PII> q;
	q.push({
      a,0 });
	isprime[a] = false;
	while (!q.empty())
	{
     
		auto num = q.front();q.pop();
		if (num.first == b) return num.second;
		//1.改变个位数
		int tmp1 = (num.first / 10) * 10;
		for (int i = 0;i < 10;i++)
		{
     
			int cnt1 = tmp1 + i;
			if (isprime[cnt1])
			{
     
				isprime[cnt1] = false;
				q.push({
     cnt1,num.second+1});
			}
		}
		//2.改变十位数
		int tmp2 = (num.first / 100) * 100 + num.first % 10;
		for (int i = 0;i < 10;i++)
		{
     
			int cnt2 = tmp2 + i * 10;
			if (isprime[cnt2])
			{
     
				isprime[cnt2] = false;
				q.push({
     cnt2,num.second + 1});
			}
		}
		//3.改变百位数
		int tmp3 = (num.first / 1000) * 1000 + num.first % 100;
		for (int i = 0;i < 10;i++)
		{
     
			int cnt3 = tmp3 + i * 100;
			if (isprime[cnt3])
			{
     
				isprime[cnt3] = false;
				q.push({
      cnt3,num.second + 1 });
			}
		}
		//4.改变千位数
		int tmp4 = num.first % 1000;
		for (int i = 1;i < 10;i++)
		{
     
			int cnt4 = tmp4 + i * 1000;
			if (isprime[cnt4])
			{
     
				isprime[cnt4] = false;
				q.push({
      cnt4,num.second + 1 });
			}
		}
	}
}
int main()
{
     
	int a;
	get_prime();
	cin >> a >> b;
	int ans=bfs(a);
	cout << ans << endl;
	return 0;
}

7.洛谷1332 血色先锋队

题目传送门

题目描述

巫妖王的天灾军团终于卷土重来，血色十字军组织了一支先锋军前往诺森德大陆对抗天灾军团，以及一切沾有亡灵气息的生物。孤立于联盟和部落的血色先锋军很快就遭到了天灾军团的重重包围，现在他们将主力只好聚集了起来，以抵抗天灾军团的围剿。可怕的是，他们之中有人感染上了亡灵瘟疫，如果不设法阻止瘟疫的扩散，很快就会遭到灭顶之灾。大领主阿比迪斯已经开始调查瘟疫的源头。原来是血色先锋军的内部出现了叛徒，这个叛徒已经投靠了天灾军团，想要将整个血色先锋军全部转化为天灾军团！无需惊讶，你就是那个叛徒。在你的行踪败露之前，要尽快完成巫妖王交给你的任务。
军团是一个 n 行 m 列的矩阵，每个单元是一个血色先锋军的成员。感染瘟疫的人，每过一个小时，就会向四周扩散瘟疫，直到所有人全部感染上瘟疫。你已经掌握了感染源的位置，任务是算出血色先锋军的领主们感染瘟疫的时间，并且将它报告给巫妖王，以便对血色先锋军进行一轮有针对性的围剿。

输入格式

第 1 行：四个整数 n，m，a，b，表示军团矩阵有 n 行 m 列。有 a 个感染源，b 为血色敢死队中领主的数量。
接下来 a 行：每行有两个整数 x，y，表示感染源在第 x 行第 y 列。
接下来 b 行：每行有两个整数 x，y，表示领主的位置在第 x 行第 y 列。

输出格式

第 1 至 b 行：每行一个整数，表示这个领主感染瘟疫的时间，输出顺序与输入顺序一致。如果某个人的位置在感染源，那么他感染瘟疫的时间为 0。

输入输出样例
输入

5 4 2 3
1 1
5 4
3 3
5 3
2 4

输出

3
1
3

说明/提示

输入输出样例 1 解释
如下图，标记出了所有人感染瘟疫的时间以及感染源和领主的位置。

数据规模与约定

对于$100$% 的数据，保证 $1\le n,m\le 500，1\le n,m\le 500$，$1\le a,b\le 10^5,1\le a,b\le 10^5$ 。

题目大意：
中文题意，输出每个国王最早感染的时间。

解题思路：
$BFS$ 求最短路的题目一般都是从一个点到另一个点，经过能走的点绕过不能走的点，搜索出最短的路径。这道题不同于以往的是要同时从多个点往外扩散，找到到达目标点的最短路径，并依次输出最短距离。有一种方式就是，在 $BFS$ 前就先将所有已经感染的点放进队列里，依次搜索队列里的即可，其他操作和普通的 $BFS$ 一样。

上代码：

#include
using namespace std;
const int N = 510;
typedef pair<int,int> PII;
int n,m,a,b;
int dist[N][N];
queue<PII> q;
bool vis[N][N];
int dx[]={
     0,1,0,-1};
int dy[]={
     1,0,-1,0};
void bfs()
{
     
	while(q.size())
	{
     
		PII t = q.front();q.pop();
		for(int i = 0;i < 4;i++)
		{
     
			int x = t.first + dx[i],y = t.second + dy[i];
			if(x >= 1 && x <= n && y >= 1 && y <= m && !vis[x][y])
			{
     
				dist[x][y] = min(dist[x][y],dist[t.first][t.second]+1);;
				vis[x][y] = true;
				q.push({
     x,y});
			}	
		}
	}
}
int main()
{
     
	scanf("%d%d%d%d",&n,&m,&a,&b);
	memset(dist,0x3f,sizeof dist);
	for(int i = 1;i <= a;i++)
	{
     
		int x,y;
		scanf("%d%d",&x,&y);
		q.push({
     x,y});
		vis[x][y] = true;//标记已被感染的位置
		dist[x][y] = 0; 
	}
	bfs();
	for(int i = 1;i <= b;i++)
	{
     
		int x,y;
		scanf("%d%d",&x,&y);
		printf("%d\n",dist[x][y]);
	}
	return 0;
}

8、UPC Contest2623 - 2020年混合个人训练第九十场 C:最少转弯问题 (turn)（BFS记录转弯次数）

问题描述

给出一张地图，这张地图被分为n*m(n,m≤100）个方块，任何一个方块不是平地就是高山。平地可以通过，高山则不能。现在你处在地图的(x1,y1)这块平地，问：你至少需要拐几个弯才能到达目的地(x2,y2)？你只能沿着水平和垂直方向的平地上行进，拐弯次数就等于行进方向的改变（从水平到垂直或从垂直到水平）的次数。例如：如图 8-6，最少的拐弯次数为5。

输入

输入将遵循以下格式：

a数组为整个地图地形描述（0：空地；1：高山）。

样例输入

5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7

样例输出

5

解题思路：
和一般的BFS一样的操作，只是在搜索的时候，对于某一个方向只要能走就一直走，并记录最小转弯次数，将该方向上的次数更新为由上一个方向到这个方向加一。

上代码：

#include
using namespace std;
typedef pair<int,int> PII;
int g[110][110];
int dx[] = {
     0,1,0,-1};
int dy[] = {
     1,0,-1,0};
bool vis[110][110];
map<PII,int> dist;
int start_x,start_y,end_x,end_y;
int n,m;
void bfs(int sx,int sy)
{
     
    queue<PII> q;
    q.push({
     sx,sy});
    dist[{
     sx,sy}]=0;
    while(q.size())
    {
     
        PII t = q.front();q.pop();
        for(int i = 0;i < 4;i++)
        {
     
            int x = t.first + dx[i];
            int y = t.second + dy[i];
            while(x>=1&&x<=n&&y>=1&&y<=m&&!g[x][y])
            {
     
                if(!vis[x][y])
                {
     
                    if(x == end_x && y == end_y)
                    {
     
                        printf("%d",dist[t]);
                        return;
                    }
                    vis[x][y] = true;
                    dist[{
     x,y}] = dist[t] + 1;
                    q.push({
     x,y});
                }
                x = x + dx[i];
                y = y + dy[i];
            }
        }
    }
    return;
}
int main()
{
     
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++)
    {
     
        for(int j = 1;j <= m;j++)
        {
     
            scanf("%d",&g[i][j]);
        }
    }
    scanf("%d%d%d%d",&start_x,&start_y,&end_x,&end_y);
    bfs(start_x,start_y);
    return 0;
}

9、Contest2633 - 2020年混合个人训练第九十二场 问题 F: 二师兄的纪录片（带传送门的BFS）

题目描述

二师兄护送师傅取经成功之后，成了名人，他决定重新把取经的路再走一遍，并且拍摄一部纪录片宣传路上的风光。
从东土大唐到天竺的地图，是正方形的，城市坐落在 N 行 N 列的方形地图上。地图从位置（1，1）排列到位置（N，N）。地图上每一个格子是一座城市，上下左右直接相邻的城市之间可以一天到达。
有 P 座城市住着野蛮人（野蛮城市），他们只吃红烧肉。一天三顿红烧肉，连早餐都吃红烧肉。二师兄是出家人，决定不去这些城市.
另有 Q 座城市（友好城市）希望二师兄帮他们多宣传城市风光，所以给二师兄提供一个优惠条件：如果二师兄在这座城市（X）停留三天，就可以在第四天派专机把二师兄送到另外一座城市 Y。从城市 X 飞到城市 Y 可以瞬间完成，即：二师兄在到达X城市后，可以选择四天后到达Y城市。当然，二师兄也可以选择只在X城市停留一天，然后访问X城市直接相邻的城市。
已知长安城位于地图的（1，1）位置，目的地灵山位于地图的 （N，N）位置。每一个友好城市只能直飞到另外一个城市。
请求出二师兄从长安到达灵山最少需要多少天。

输入

输入数据第一行有三个整数，分别是 N，P，Q。
整数之间用空格分开。城市坐标系X轴向下，起点为1，Y 轴向右，起点为1。
数据接下来的 P 行，每行两个整数 a,b，代表某一个野蛮城市的坐标 (a,b)。
位置信息 (a,b) 表示在 X-Y 坐标系中的位置。
再接下来的 Q 行，每行四个整数，代表友好城市 X 的坐标和从X能直飞的城市 Y 的坐标。

输出
输出数据一行，表示二师兄从长安去往灵山最少需要多少天。
如果从长安到达不了灵山，则输出-1。
二师兄在长安出发那天记为第1天，到达灵山那天的日期就是输出数据。

样例输入

【样例1】
5 7 0
1 2
2 4
3 2
3 4
4 2
4 4
5 4
【样例2】
9 27 1 
1 2 
1 6 
2 4 
2 6 
2 8 
3 2 
3 4 
3 6 
3 8 
4 2 
4 4 
4 6 
4 8 
5 4 
5 6 
5 8 
6 4 
6 6 
6 8 
7 4 
7 6 
7 8 
8 4 
8 6 
8 8 
9 4 
9 8 
6 2 8 9

样例输出

【样例1】
11
【样例2】
12

提示

样例1解释样例数据后面的解释说明当中，“.”代表可以访问的普通城市，“#”代表野蛮城市。“1”代表X城市和能从“1”直飞的城市Y。
原地图：
样例1原地图.png
到达目的地的走法：

样例2解释样例数据后面的解释说明当中，“.”代表可以访问的普通城市，“#”代表野蛮城市。“1”代表X城市和能从“1”直飞的城市Y。
原地图：

走法说明：走到 6 2 点的时候，穿越到 8 9 点。

解题思路：对于可直达的这种情况，再搜寻完四个方向后，单独考虑步数是否更优，若更优则更新步数并加入队列继续搜索。
需要注意的是：这里的“传送门”的单向的；普通的走法有可能比经过传送门的方式更优。

上代码：

#include 
using namespace std;
const int M = 110;
typedef pair<int,int> PII;
bool g[M][M];
int dx[]={
     0,1,0,-1};
int dy[]={
     1,0,-1,0};
int N,P,Q,X[M],Y[M],dist[M][M];
map<PII,int> mp;
inline int read()
{
     
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){
     if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){
     x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
queue<PII> q;
int bfs()
{
     
    memset(dist,0x3f,sizeof dist);
    q.push({
     1,1});
    dist[1][1] = 1;
    while(q.size())
    {
     
        PII t = q.front();q.pop();
        int t_x = t.first;
        int t_y = t.second;
        int distance = dist[t_x][t_y];
        if(t_x == N && t_y == N){
     
            return distance;
        }
        for(int i = 0;i < 4;i++)
        {
     
            int xx = t_x + dx[i];
            int yy = t_y + dy[i];
            if(xx >= 1 && xx <= N && yy >= 1 && yy <= N && !g[xx][yy])
            {
     
                if(dist[xx][yy] > dist[t_x][t_y] + 1){
     
                    dist[xx][yy] = dist[t_x][t_y] + 1;
                    q.push({
     xx,yy});
                }
            }
        }
        if(mp[{
     t_x,t_y}])
        {
     
            int idx = mp[{
     t_x,t_y}];
            if(dist[X[idx]][Y[idx]] > dist[t_x][t_y] + 4 && !g[X[idx]][Y[idx]])
            {
     
                dist[X[idx]][Y[idx]] = dist[t_x][t_y] + 4;
                q.push({
     X[idx],Y[idx]});
            }
        }
    }
    return -1;
}
int main()
{
     
    N=read(),P=read(),Q=read();
    while(P--)
    {
     
        int x,y;
        x=read(),y=read();
        g[x][y] = true;
    }
    for(int i = 1;i <= Q;i++)
    {
     
        int x,y;
        x=read(),y=read();
        X[i]=read(),Y[i]=read();
        mp[{
     x,y}] = i;
    }
    int ans=bfs();
    cout<<ans<<endl;
    return 0;
}

2020.11.24更。

持续更新中。。。
待续。。。