遗传算法

利用遗传算法计算x^10+ex=100的解

照例，import一些必要的库

%matplotlib inline 
import numpy as np
import matplotlib.pyplot as plt
import random

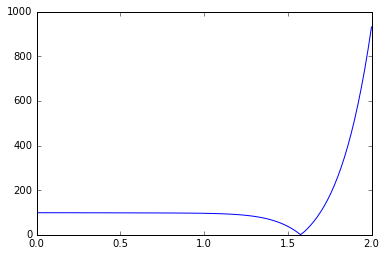
不管怎么着，先把图画出来，看一下大概的取值区间

x=np.linspace(0,2,100)
def y(x):
    return np.abs(x**10+np.exp(x)-100)

plt.plot(x,y(x))
plt.show()

为了方便编码（其实是我懒），决定取值区间为[0,2]。

下面进行编码，采用32位的编码。也就是将[0,2]分割成2^32个小区段。

比如[0,0,0,...,0]是0，[1,0,0,...0]是2^(-31)

sons=np.zeros([100,32])
values=np.zeros([100])
results=np.zeros([100])
sort_index=np.zeros([100])

初始化函数，先随机生成100个点。

def init():
    global sons
    for i in range(100):
        for j in range(32):
            sons[i][j]=random.randint(0,1)

计算函数，将对应的编码转换成相应的数值

def cmp(son):
    value=0
    temp=2**(-31)
    for i in son:
        value+=i*temp
        temp*=2
    return value

更新数值的函数

def update():
    global sons,values
    for i in range(100):
        values[i]=cmp(sons[i])

遗传算法的核心函数，首先找出最接近解的10个值，然后利用这十个值的编码产生其余九十个值的编码。

具体操作是，随机选取前十个中的两个，分别将他们的奇数编码和偶数编码组合生成一个新的编码。

为了能够进化，也就是不局限于起初产生的编码，加入了突变这一因素。

同时为了确保函数的收敛速度，针对不同的编码提供不同的突变。

较接近解的编码，不允许出现大突变，其余允许大突变，防止陷入局部最优解。(在求最大值最小值的时候)

def gen():
    global values,sort_index,results,sons
    results=np.abs(values**10+np.exp(values)-100)
    sort_index=np.argsort(results)
    for i in range(100):
        if i in sort_index[:10]:
            continue
        else:
            sam=random.sample(list(sort_index[:10]),2)
            sons[i][::2]=sons[sam[0]][::2]
            sons[i][1::2]=sons[sam[1]][1::2]
    for i in range(500):
        index=random.randint(0,99)
        if index in sort_index[0:3]:
            flag=random.randint(0,1)
            sons[index][flag]=1-sons[index][flag]
        elif index in sort_index[3:10]:
            flag=random.randint(0,7)
            sons[index][flag]=1-sons[index][flag]
        else:
            flag=random.randint(0,31)
            sons[index][flag]=1-sons[index][flag]   
    return(results[sort_index[0]],values[sort_index[0]])
    

main函数

def main():
    init()
    for i in range(1001):
        update()
        a,b=gen()
        if i%250==0:
            print(a,b)
            plt.plot(values,y(values),'.',x,y(x))
            plt.show()

main()

4.53816371162 1.58435669821

0.000244704122139 1.57704925584

0.000244420886716 1.57704925537

0.000244420886716 1.57704925537

2.94243349686e-07 1.57704885304

可以看到，函数迅速收敛，最后的误差已经很小了，只有10^(-7)这个数量级。

如果想要更精确的结果可以多迭代几次，可以很快地找出在32位精度下的最优解。

请不要在意那些离散在外面的点，那是因为允许大的突变而产生的，在有多个极值的情况下，它们的作用就大了。