基于加入差分进化策略的杂草算法的WSN节点的部署优化
文章目录
- 一、理论基础
-
- 1、入侵杂草算法
- 2、差分进化策略
- 二、仿真结果与分析
- 三、参考文献
- 四、Matlab程序
一、理论基础
受文献[1]的启发，将差分进化算法的策略应用到入侵杂草算法当中，仿真结果表明，与原来的杂草算法相比，WSN节点部署覆盖率有很大提升。
1、入侵杂草算法
请参考这里。
2、差分进化策略
差分进化算法（Differential Evolution，DE）主要包括变异、交叉和选择3个典型进化算子，具有记忆个体最优解以及受控数少、全局收敛性强等优点。为了解决IWO的缺点，将DE的变异、交叉、选择操作引入到IWO中，具体操作如下：
①种子变异。经过空间扩散过程后变异操作的种子为 U i = X z 1 + F ( X z 2 − X z 3 ) (1) U_i=X_{z1}+F(X_{z2}-X_{z3})\tag{1} Ui=Xz1+F(Xz2−Xz3)(1)式中： F F F为缩放因子， F ∈ [ 0 , 2 ] F∈[0,2] F∈[0,2]； X z 1 , X z 2 , X z 3 X_{z1},X_{z2},X_{z3} Xz1,Xz2,Xz3为杂草 x i x_i xi生成的3个种子。
②种子交叉。对第 t t t代的 X i ( t ) X_i(t) Xi(t)以及 Y i ( t ) Y_i(t) Yi(t)进行如下式的交叉操作，该操作可以进一步提高算法种群的多样性。 U i j = { Y i , j ( t ) r a n d ( 0 , 1 ) ≤ C R X i , j ( t ) r a n d ( 0 , 1 ) > C R (2) U_{ij}=\begin{dcases}Y_{i,j}(t)\quad\,\, rand(0,1)≤CR\\X_{i,j}(t)\quad rand(0,1)>CR\end{dcases}\tag{2} Uij={ Yi,j(t)rand(0,1)≤CRXi,j(t)rand(0,1)>CR(2)
③种子选择。 X i = { U i , j f ( U i , j ) > f ( X i ) X i , j f ( U i , j ) ≤ f ( X i ) (3) X_i=\begin{dcases}U_{i,j}\quad f(U_{i,j})>f(X_i)\\X_{i,j}\quad f(U_{i,j})≤f(X_i)\end{dcases}\tag{3} Xi={ Ui,jf(Ui,j)>f(Xi)Xi,jf(Ui,j)≤f(Xi)(3)
二、仿真结果与分析
使用与文献[2]相同的覆盖模型，与经典的杂草算法进行对比，分以下两个场景进行仿真分析。
①监测区域 20 m × 20 m 20m×20m 20m×20m，部署节点总数为24，感知半径为2.5m，通信半径为5m，感知误差半径为0.05m。种群规模为30，分别循环20次，每次迭代300次，覆盖率取平均值。
图1显示了二者覆盖率的变化情况，显然DE_IWO算法优于原始IWO算法。
图2和图3分别为IWO和DE_IWO算法的优化覆盖图。
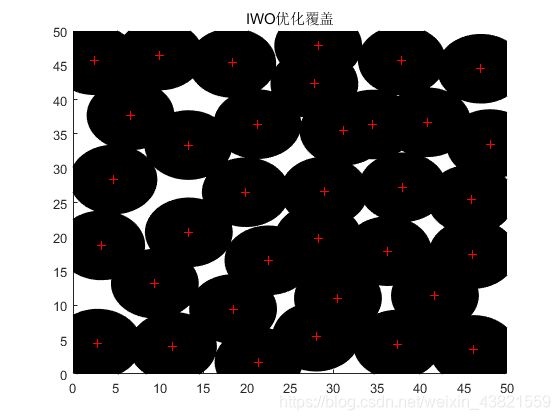
②监测区域 50 m × 50 m 50m×50m 50m×50m，部署节点总数为35，感知半径为5m，通信半径为10m，感知误差半径为0.1m。种群规模为30，分别循环20次，每次迭代300次，覆盖率取平均值。
图4显示了二者覆盖率的变化情况，显然DE_IWO算法优于原始IWO算法。
图5和图6分别为IWO和DE_IWO算法的优化覆盖图。
三、参考文献
[1] 范宏, 刘自超, 郭翔. 基于差分进化入侵杂草算法的含分布式电源配电网重构[J]. 可再生能源, 2019, 37(04):75-81.
[2] 徐钦帅, 何庆, 魏康园. 改进蚁狮算法的无线传感器网络覆盖优化[J]. 传感技术学报, 2019, 32(02):266-275.
四、Matlab程序
下载地址：
https://download.csdn.net/download/weixin_43821559/18180330