智能优化算法应用：基于麻雀搜索算法的积分计算 -附代码

智能优化算法应用：基于麻雀搜索算法的积分计算

摘要：本文提出了一种基于麻雀搜索算法的积分计算算法。该方法的基本思路是: 先在积分区间内产生一些随机分割点( 不一定是等距分割点)，然后用麻雀优化算法对这些分割点进行优化，将优化后得到的最优分割点从小到大排序并作为该区间的分割点，这些分割点结合 Simpson3/8 积分公式进行数值计算。

1.麻雀优化算法

麻雀搜索算法具体原理请参照：https://blog.csdn.net/u011835903/article/details/108830958

2.基于麻雀搜索算法的积分计算原理和步骤

提出的基于麻雀算法求任意函数数值积分算法流程可归结如下:

Step1：初始化麻雀搜索算法相关参数，如种群数量，搜索维度等。在被积区间内［a，b］​随机生成初始种群
$$X=(X_1,X_2,...,X_N)\text{\hspace{1em}(1)}$$
其中:$X_i=(X_{i1},X_{i2},...,X_{in});X_{ik}\in [a,b]$表示第 $k$ 个节点，$n$表示积分区间内的节点数。

Step2:计算适应度并进行排序。先将随机产生的每个个体置于积分区间的左右端点之间，并按照升序排列，这样就得到 $n+2$个节点和 $n+1$ 小段，再分别计算这 $n+2$ 个节点相邻节点之间的距离 $d_j,j=1,2,\dots ,n+1$及这$n+2$个节点对应的函数值和每小段中点对应的函数值，确定每小段左右端点和中间点的 3个函数值中，记下最大函数值$max,Y_j
$ 、最小函数值$min{Y}_j,j=1,2,\dots ,n+1$． 并定义适应度为:
$$f_j=\sum _{j=1}^{n+1}|max{Y}_j-min{Y}_j|d_j\text{\hspace{1em}(2)}$$
越小表明分割方法越好。

Step3:根据计算的适应度

Step4:根据麻雀算法位置更新公式更新位置

Step5：计算适应度值，并更新最优位置

Step6：若未达到最大迭代次数 $T_{max}$ ，则返回步骤4;否则，输出全局最优位置;

Step7:计算定积分值。将所求的最优分割点$[a,x_1,...,x_n,b]$,分别代入数值积分式进行计算$(a=x_0,b=x_{n+1})$，得出:
$$J_1=\sum _{j=0}^{n+1}\{f(x_{j+1})+f(x_j)\}\ast d_j/2\text{\hspace{1em}(3)}$$

$$J_2=\sum _{j=0}^{n+1}\{f(x_{j+1})+4f(\frac{x_{j+1}+x_j}{2})+f(x_j)\}\ast d_j/6\text{\hspace{1em}(3)}$$

$$J3=\sum _{j=0}^{n+1}\{f(x_{j+1})+3f(\frac{2x_{j+1}+x_j}{3})+3f(\frac{x_{j+1}+2x_j}{3})+f(x_j)\}\ast d_j/8\text{\hspace{1em}(4)}$$

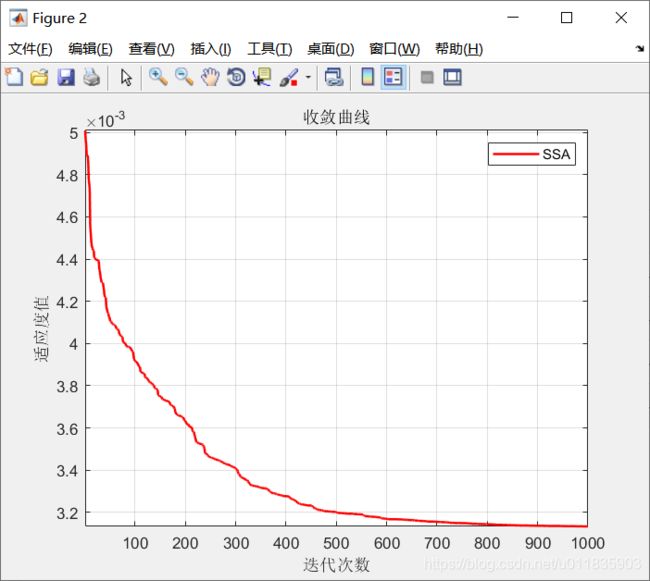
3.算法实验

为了验证本文提出算法的有效性和正确性，选取了几个典型的数值积分函数。取 N= 20，D = 60，分别计算 6 个函数的在[0,2]的积分值。函数信息如下：
$$f1=x^2\text{\hspace{1em}(5)}$$

$$f2=x^4\text{\hspace{1em}(6)}$$

$$f3=\sqrt{1+x^2}\text{\hspace{1em}(7)}$$

$$f4=\frac{1}{x+1}\text{\hspace{1em}(8)}$$

$$f5=sin(x)\text{\hspace{1em}(9)}$$

$$f6=e^x\text{\hspace{1em}(10)}$$

名称	f1	f2	f3	f4	f5	f6
理论精确解	2.667	6.400	2.958	1.099	1.416	6.389
麻雀计算法得到的J1	2.6674	6.404	2.9581	1.0987	1.4158	6.3896
麻雀计算法得到的J2	2.6667	6.400	2.9579	1.0986	1.4161	6.3891
麻雀计算法得到的J3	2.6667	6.400	2.9579	1.0986	1.4161	6.3891

收敛曲线如下图所示：

4.参考文献：

[1]黄基诞.基于改进灰狼优化算法的积分计算实验[J].实验室研究与探索,2020,39(11):16-19+66.

5.Matlab代码

https://mianbaoduo.com/o/bread/YZeZlZ9y