专题五数据分析与多项式计算

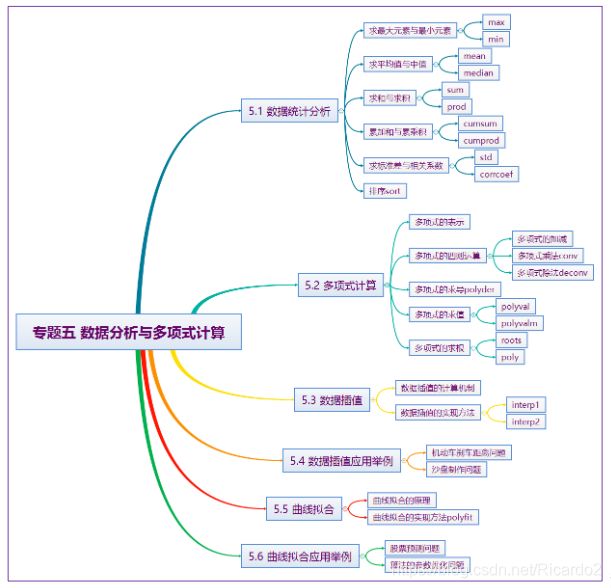
数据分析与多项式计算

---

一、数据统计分析

1、求矩阵的最大元素与最小元素

max()：求向量或矩阵的最大元素。
min()：求向量或矩阵的最小元素。

• 当参数为向量时，有两种调用格式：
  (1)y=max(X)：返回向量X的最大值存入y，如果X中包含复数元素，则按模取最大值。
  (2)[y,k]=max(X)：返回向量X的最大值存入y，最大值元素的序号存入k,如果X中包含复数元素，则按模取最大值。
  
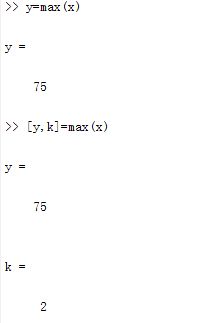
• 当参数为矩阵时，有三种调用格式：
  (1)max(A)：返回一个行向量，向量的第i个元素是矩阵A的第i列上的最大值。
  (2)[Y,U]=max(A)：返回行向量Y和U，Y向量纪录A中每列的最大值，U向量记录每列最大值元素的行号。
  (3)max(A,[],dim)：dim取1或2。dim取1时，该函数功能与max(A)相同；当dim取2时，该函数返回一个列向量，其第i个元素是矩阵A的第i列上的最大值。
  例子：求矩阵A=[13,-56,78;25,63,-235;78,25,563;1,0,-1]每行每列的最大元素，以及整个矩阵的最大元素。
  
  

2、求矩阵的平均值与中值

• 平均值：算术平均值，值每项数据之和除以项数。用mean()函数。
• 中值：数据序列中其值的大小恰好处在中间的元素。如果数据个数为奇数，则取值为位于中间的元素；如果数据个数为偶数，则取值为中间两个元素的平均值。用median()函数。
  

3、求和与求积

• sum()：求和函数
• prod()：求积函数

4、累加和与累乘积

cumsum()：累加和函数
cumprod()：累乘积函数

5、求标准差与相关系数

• 标准差用于计算数据偏离平均数的距离的平均值，计算公式为
  
  计算标准差的函数为std()，调用格式为：
  (1)std(X)：计算向量X的标准差。
  (2)std(A)：计算矩阵A的各列的标准差。
  (3)std(A,flag,dim)：当flag取0时，按S1所列公式计算样本标准方差；当flag取1时，按S2所列公式计算总体标准方差。默认情况下，flag=0，dim=1.
  
• 相关系数能反映两组数据序列之间相互关系，其计算公式为
  
  计算相关系数函数为corrcoef()：
  (1)corrcoef(A)：返回由矩阵A所形成的一个相关系数矩阵。其中，第i行第j列的元素表示原矩阵A中第i列和第j列的相关系数。
  (2)corrcoef(X,Y)：在这里X，Y是向量，与corrcoef([X,Y])的作用一样，用于求X、Y向量之间的相关系数。
  例子：评估哪个产品分配方案最为合理。
  
  

6、排序

• sort(X)：对向量X按升序排列
• [Y,I]=sort(A,dim,mode)：其中dim指明对A的列还是行进行排序。mode指明按升序还是降序，若取“ascend”为升序，若“descend”为降序，默认为升序。输出参数中，Y是排序后的矩阵，I记录Y中的元素在A中的位置。
  
  

二、多项式计算

1、多项式的表示

n次多项式：f(x)=a_nxⁿ+a_n-1x^n-1+……+a₁x+a₀
在MATLAB中，f(x)表示为向量形式[a_n,a_n-1,……,a₁,a₀]
在MATLAB中创建多项式向量时，需要注意：
(1)多项式系数向量的顺序是从高到低。
(2)多项式系数向量包含0次项系数，所以其长度为多项式最高次数加1.
(3)如果有的项没有，系数向量相应位置应用0补足。

2、多项式的四则运算

(1)多项式的加减运算
相应的向量相加减。注意，只有同次项才能相加减。不足的项添0。
(2)多项式乘法
conv(P1,P2)：多项式相乘。其中，P1，P2是两个多项式系数向量。
(3)多项式除法
[Q,r]=deconv(P1,P2)：多项式相除，Q返回多项式P1除以P2的商式，r返回余式。Q和r仍是多项式系数向量。deconv是conv的逆函数，因此下式成立：P1=conv(Q,P2)+r
例子：f(x)=3x⁵-5x⁴-7x²+5x+6，g(x)=3x²+5x-3，求f(x)+g(x),f(x)-g(x),f(x)*g(x),f(x)/g(x)

3、多项式的求导

(1)polyder( P)：求多项式P的导函数。
(2)polyder( P,Q)：求P*Q的导函数。
(3)[p,q]=polyder( P,Q)：求P/Q的导函数，导函数的分子存入p，分母存入q。
例子：已知两个多项式
a(x)=3x³+x²-6；b(x)=x+2
计算两个多项式的乘积的导函数、商的导函数。

4、多项式的求值

(1)polyval(p,x)：代数多项式求值，其中p为多项式系数向量，x可以是标量、向量或者矩阵。若x为标量，则求多项式在该点的值；若x为向量或矩阵，则对向量或矩阵中的每个元素求多项式。
(2)polyvalm(p,x)：矩阵多项式求值，其中x要求为方阵，以方阵为自变量求多项式的值。

• 若x都为方阵，对比polyval和polyvalm。ployval执行的是点乘运算，而polyvalm执行的是矩阵运算。
  设A为方阵，P代表多项式x³-5x²+8，那么polyvalm(P,A)的含义是：
  A³-5A²+8 * eye(size(A))
  而ployval(P,A)的含义是：A.³-5A.²+8*ones(size(A))

例子：P为多项式x⁴+8x³-10，x为方阵[-1,1.2;2,-1.8]

5、多项式的求根

(1)roots( p)：多项式求根函数
例子：求多项式x⁴+8x³-10的根

(2)若一直多项式的全部根x，poly(x)函数建立起该多项式.

(3)求函数p(x)=-38.89x²+126.11x-3.42在[0.2]区间上的最大值。

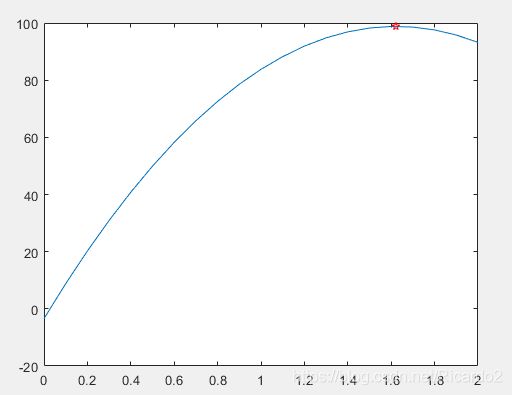
三、数据插值

从数学上分析，数据插值是一种函数逼近的方法。对于已知的点列[(x₁,y₁),(x₂,y₂),……,(x_n,y_n)]，其中x与y对应的函数关系y=f(x)是一个未知函数。在此，我们构造一个近似函数g(x)≈f(x)，满足g(x_i)=y_i(i=1,2,……,n)。具体构造方式不在此介绍。

1、一维插值函数

MATLAB提供一维插值函数：Y1=interpl(X,Y,X1,method)
该语句将根据X、Y的值，计算函数在X1处的值。其中，X、Y是两个等长的已知向量，分别表示采样点和采样值。X1是一个向量或标量，表示要插值的点。
(1)method参数用于指定插值方法，常用得有四种：

• linear：线性插值，此为默认方法。将与插值点靠近的两个数据点用直线连接，然后在直线上选取对应插值点的数据。
• nearest：最近点插值。选择最近样本点的值作为插值数据。
• pchip：分段3次埃尔米特插值。采用分段三次多项式，除满足插值条件，还需要满足在若干节点处相邻插值函数的一阶导数相等，使得曲线光滑的同时，还具有保形性。
• spline：3次样条插值。每个分段内构造一个三次多项式，使其插值函数除满足插值条件外，还要求在各节点处具有连续的一阶和二阶导数。
  （多项式次数并非越高越好，次数越高，越容易产生震荡而偏离原函数，称为Runge现象。取3次是比较合适的。）

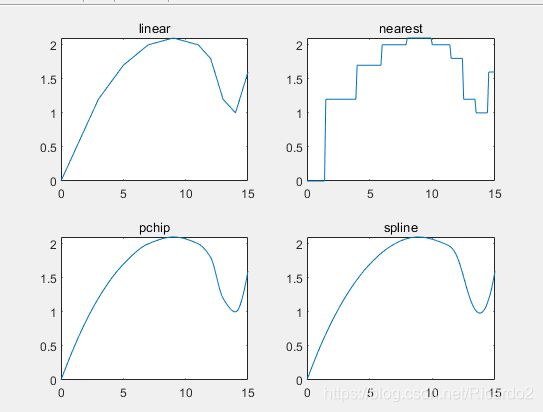
例子：对比四种插值

x= [0,3,5,7,9,11,12,13,14,15];
y=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
x1=0:0.1:15;
subplot(2,2,1)
y1=interp1(x,y,x1,'linear');
plot(x1,y1)
title('linear')
subplot(2,2,2)
y1=interp1(x,y,x1,'nearest');
plot(x1,y1)
title('nearest')
subplot(2,2,3)
y1=interp1(x,y,x1,'pchip');
plot(x1,y1)
title('pchip')
subplot(2,2,4)
y1=interp1(x,y,x1,'spline');
plot(x1,y1)
title('spline')

(2)四种方法的比较

• 线性插值和最近点插值方法比较简单。其中线性插值方法的计算量与样本点n无关。n越大，误差越小。
• 3次埃尔米特插值和3次样条插值都能保证曲线的光滑性。相比较而言，3次埃尔米特插值具有保形性；而3次样条插值要求其二阶导数也连续，所以插值函数的性态更好。

2、二维插值函数

Z1=interp2(X,Y,Z,X1,Y1,method)
其中，X、Y是两个向量，表示两个参数的采样点。Z是采样点对应的函数值。X1、Y1是两个向量或标量，表示要插值的点。
不支持pchip方法。
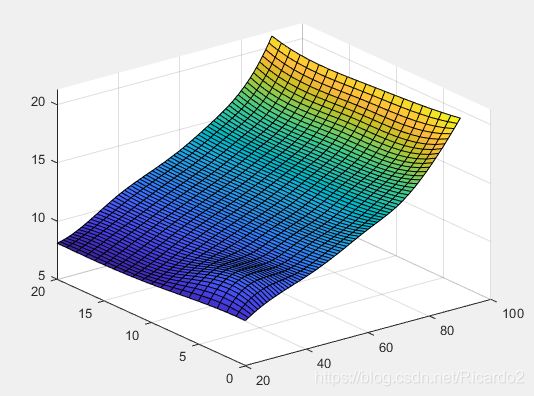
例子：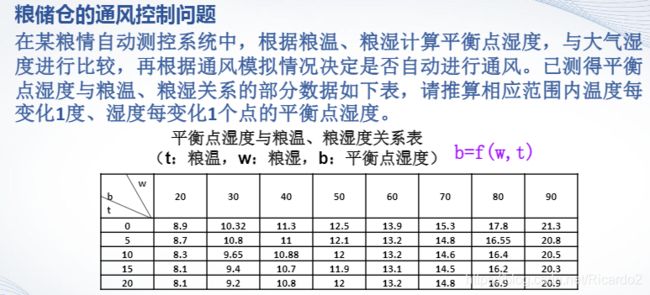

x=20:10:90;
y=(0:5:20)';
z=[8.9,10.32,11.3,12.5,13.9,15.3,17.8,21.3;8.7,10.8,11,12.1,13.2,14.8,16.55,20.8;8.3,9.65,10.88,12,13.2,14.6,16.4,20.5;8.1,9.4,10.7,11.9,13.1,14.5,16.2,20.3;8.1,9.2,10.8,12,13.2,14.8,16.9,20.9];
xi=20:90;
yi=(0:20)';
zi=interp2(x,y,z,xi,yi,'spline');
surf(xi,yi,zi)

四、数据插值应用举例

1、机动车刹车距离问题

分析：设d=有效视距，d1=反应距离，d2=制动距离，d3=安全距离，v=行驶速度，t=反应时间
其中，d1=t*v；d2与v有关，但关系式d2(v)未知。
(1)建立方程：10v+d2(v)+10=120，利用数据插值方法，求得v-d的拟合曲线
(2)由已知的d=120，求得对应的v（v取整数）。
(3)在d-v拟合曲线中找到 v=125对应的d

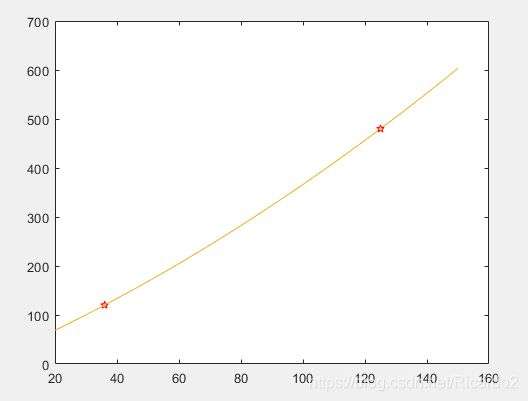
v=20:10:150;
vs=v.*(1000/3600);
d1=10.*vs;
d2=[3.15,7.08,12.59,19.68,28.34,38.57,50.4,63.75,78.71,95.22,113.29,132.93,154.12,176.87];
d3=10;
d=d1+d2+d3;
vi=20:1:150;
di=interp1(v,d,vi,'spline');
%求d=120对应的整数v
x=abs(di-120);
[y,i]=sort(x);%将x按升序排列
vi(i(1))%x中最小元素的序号i(1)，即是d=120对应的整数速度v
plot(vi,di,vi(i(1)),di(i(1)),'rp')
%求v=125对应的d
j=find(vi==125);
di(j)%求得d=480.1373
hold on
plot(vi,di,vi(j),di(j),'rp')

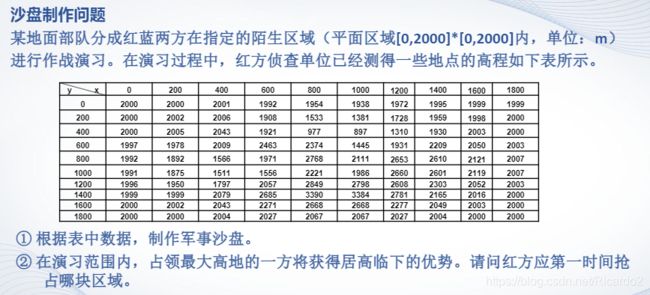
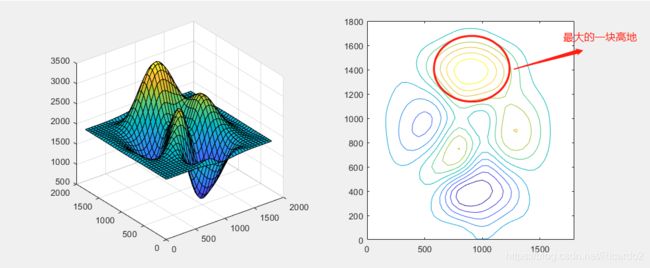
2、沙盘制作问题

x=0:200:1800;
y=x.';
z=[2000,2000,2001,1992,1954,1938,1972,1995,1999,1999;2000,2002,2006,1908,1533,1381,1728,1959,1998,2000;
2000,2005,2043,1921,977,897,1310,1930,2003,2000;1997,1978,2009,2463,2374,1445,1931,2209,2050,2003;  1992,1892,1566,1971,2768,2111,2653,2610,2121,2007;1991,1875,1511,1556,2221,1986,2660,2601,2119,2007;
1996,1950,1797,2057,2849,2798,2608,2303,2052,2003;1999,1999,2079,2685,3390,3384,2781,2165,2016,2000;
2000,2002,2043,2271,2668,2668,2277,2049,2003,2000;2000,2000,2004,2027,2067,2067,2027,2004,2000,2000];
x1=0:50:1800;
y1=x1';
z1=interp2(x,y,z,x1,y1,'spline');
subplot(1,2,1)
surf(x1,y1,z1);
subplot(1,2,2)
contour(x1,y1,z1,11)%绘制等高线

五、曲线拟合

曲线拟合与数据插值类似，也是一种函数逼近的方法。对于已知的点列[(x₁,y₁),(x₂,y₂),……,(x_n,y_n)]，其中x与y对应的函数关系y=f(x)是一个未知函数。在此，我们构造一个近似函数g(x)，使得误差σ_i=g(x_i)-f(x_i)在某种意义下达到最小。

1、实现方法

MATLAB中多项式拟合函数为：ployfit()，其功能为秋的最小二乘拟合多项式系数，调用格式：

(1)P=polyfir(X,Y,m)：返回次数为 n 的多项式 p(x) 的系数
(2)[P,S]=polyfir(X,Y,m)
(3)[P,S,mu]=polyfir(X,Y,m)：根据样本数据X和Y，产生一个m次多项式P及其在采样点误差数据S，mu是一个二元向量，mu(1)是mean(X)，而mu(2)是std(X)。

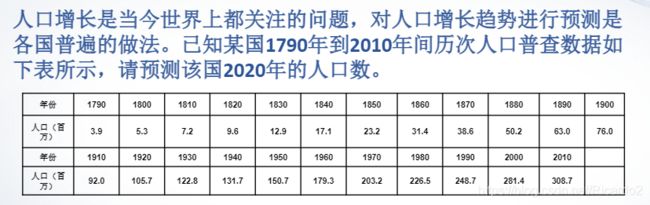
2、例子：人口增长

(1)利用曲线拟合函数

x=1790:10:2010;
y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6, 50.2,63.0,76.0,92.0,105.7,122.8,131.7,150.7,179.3,203.2,226.5,248.7,281.4,308.7];
plot(x,y,'*')
p=polyfit(x,y,3);
polyval(p,2020)
plot(x,y,'*',x,polyval(p,x));

求解得预计2020年人口总数为339.7869百万

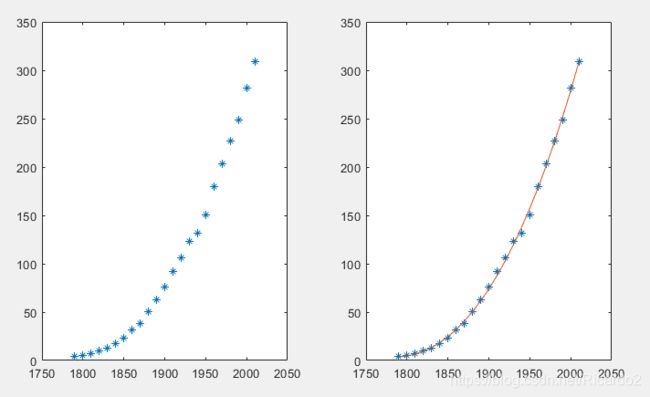
(2)根据上述拟合的曲线，计算2016年人口的误差
曲线拟合计算的2016年人口为 327.0964百万，而实际为323.1百万，误差为2.24%
(3)优化曲线，缩小上述误差
根据研究，一个国家的人口增长有如下特点：
–发展越平稳，人口增长越有规律。
–当经济发展到一定水平时，人口增长率反而下降。
总而言之，不同的环境和经济发展水平，人口
可能有不同的增长规律。因此，在人口增长数据的拟合上，应该将二战后至今这一时期的数据与此前的数据分开处理。

x=1950:10:2010;
y=[150.7,179.3,203.2,226.5,248.7,281.4,308.7];
p=polyfit(x,y,2);%采用3次，会发现第3和第2的系数为0，即次数太高。
plot(x,y,'*',x,polyval(p,x))
polyval(p,2016)
polyval(p,2020)

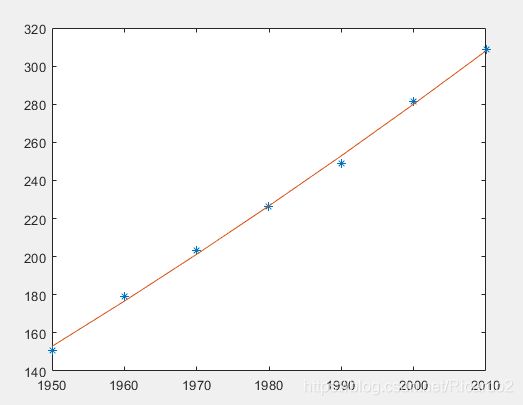
根据新的拟合，2016年的相对误差减小到0.64%。因此，优化有效。求得2020年预计人口数为 336.7857百万。
(4)总结

• 要对问题的背景进行详细分析
• 采样带你并非越多越好，根据实际情况可以减少采样点分段拟合。

3、曲线拟合与数据插值的比较

(1)相同点

• 都属于函数逼近的方法
• 都能进行数据估算

(2)不同点

• 实现方法不同：数据插值要求逼近函数经过样本点，而曲线拟合只需要总体误差最小。
• 结果形式不同：数据插值采用分段逼近，没有确定的逼近函数表达式。
• 侧重点不同：数据插值一般用于样本区间内的插值计算；曲线拟合不仅可以估算区间内其他点的函数值，还可以预测时序函数的发展趋势以及从统计数据中总结的一般性经验。
• 应用场合不同：若样本数据为精确数据，适合采用数据插值；若样本数据为统计数据或者存在误差，则适合用曲线拟合。

---

总结