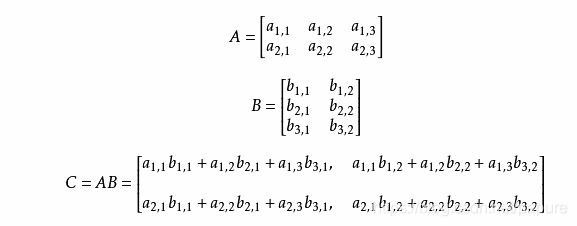C# TensorFlow 2 入门教程 - Eager Mode
C# TensorFlow 2 入门教程
二、TensorFlow.NET API
5. Eager Mode
5.1 Eager模式说明
Eager Mode 也叫做动态图模式,是TensorFlow 1.4之后版本中最重要的新特征之一,也是TensorFlow 2.0的主流写法。Eager模式是一个命令式(imperative)、运行定义式的编程形式,操作一旦从程序中调用便立即得以执行,而不再像之前那样,生成一个Tensor,通过sess.run()才能拿到值,这样使得TensorFlow的入门使用、研究和开发就更为直观。
TensorFlow 2种的动态图是优先模式,为默认开启状态,在计算时可以同时获得计算图和数值运算的结果,可以在调试的过程中实时打印出数据。
5.2 Eager模式比较
下面通过TF.NET的代码对比,方便读者直观了解TensorFlow 1.4之前的静态图和 TensorFlow 2 的Eager模式的差异点。
首先,我们在TensorFlow 1.x下实现 2.0 + 3.0 的简单加法运算。
第一步,创建计算图。
创建计算图的过程仅仅是使用各变量名创建出 “ a + b ” 加法的计算规则,记录下该公式的计算步骤,并没有传入具体的值和执行具体的计算过程。
第二步,赋值并运行计算图。
通过开启会话Session,运行公式(静态图)中的节点 “ c ”,并复制 a = 2.0 , b = 3.0 来获得 c 的数值计算结果。
完整代码如下:
using System;
using Tensorflow;
using static Tensorflow.Binding;
namespace TF_Test
{
class Program
{
//Basic Operation 2.0 + 3.0 with TensorFlow.NET 1.x
static void Main(string[] args)
{
// 1.创建计算图
// 创建2个输入端子,指定类型和名字
var a = tf.placeholder(tf.float32, name: "variable_a");
var b = tf.placeholder(tf.float32, name: "variable_b");
// 创建输出端子的运算操作,并命名
var c = tf.add(a, b, name: "variable_c");
// 2. 赋值并运行计算图
// 初始化运行环境,开启会话Session
var init = tf.global_variables_initializer();
using (var sess = tf.Session())
{
sess.run(init);//运行初始化操作,完成初始化
//给输入端子赋值
var feed_dict = new FeedItem[]
{
new FeedItem(a, 2),
new FeedItem(b, 3)
};
//运行输出端子
var c_numpy = sess.run(c, feed_dict);
//运行完输出端子,得到数值类型的 c_numpy
Console.WriteLine($"Addition with variables: {c_numpy}");
}
Console.Read();
}
}
}
可以看到,在 TensorFlow.NET 1.x 中完成简单的 2.0 + 3.0 的过程十分繁琐,后面搭建复制的神经网络模型亦是如此,这种先创建静态计算图再赋值执行的方式叫做符号式编程。
接下来,我们来看下在 TensorFlow.NET 2.0 中完成 2.0 + 3.0 运算的代码:
- TF.NET 也支持 使用 ( + , * , … ) 等算术符直接进行运算
using System;
using Tensorflow;
using static Tensorflow.Binding;
namespace TF_Test
{
class Program
{
//Basic Operation 2.0 + 3.0 with TensorFlow.NET 2
static void Main(string[] args)
{
// 创建输入张量
var a = tf.constant(2);
var b = tf.constant(3);
// 直接打印结果【也支持(+,*,...)等算术符直接进行运算】
var c = tf.add(a, b);
print($"Addition with variables: {c.numpy()}");
}
}
}
上述 2 种编程方式,都可以得到正确的结果 “Addition with variables: 5” 如下:
这种运算时同时创建计算图和计算结果的方式叫做命令式编程,TensorFlow 2 和 PyTorch 都是采用这种模式开发的,这种方式开发效率高,调试方便,所见即所得,但是运行效率可能不如静态图模式方便(后面我们会介绍如何使用 tf.function 来提高运行效率)。
5.3 Eager模式数值运算
现在,我们来演示 Eager Mode 下常见的 “ 加、减、乘、除 ” 数值运算,这串代码是通过 tf 函数 “ add、subtract、multiply、divide ”进行直接的数值运算,也可以通过运算符 “ +、-、*、/ ” 进行相同的数值操作。
常用的运算操作代码如下:
using System;
using Tensorflow;
using static Tensorflow.Binding;
namespace TF_Test
{
class Program
{
//Basic Operation add,subtract,multiply,divide
static void Main(string[] args)
{
// 定义Tensor常量类型的数值
var a = tf.constant(2);
var b = tf.constant(3);
// 张量运算操作
var add = tf.add(a, b);
var sub = tf.subtract(a, b);
var mul = tf.multiply(a, b);
var div = tf.divide(a, b);
// 访问运算结果并输出
print("add =", add.numpy());//加
print("sub =", sub.numpy());//减
print("mul =", mul.numpy());//乘
print("div =", div.numpy());//除
}
}
}
代码的执行结果如下,我们可以看到 TF.NET 正确地执行并输出了运算后的数值:
5.4 Eager模式张量降维运算
接下来,我们来演示 Eager Mode 下的 张量降维运算。
首先是模型训练过程中计算 Loss 时常用的 reduce_mean 和 reduce_sum 函数,从函数名称上可以看出来,这个函数有2个功能,降维和求平均(求和)。我们来分别讲解2个函数的定义:
tf.reduce_mean():用于计算张量 tensor 沿着指定的数轴(tensor 的某一维度)上的平均值,主要用作降维或者计算 tensor(图像)的平均值。
public Tensor reduce_mean(
Tensor[] input_tensors,
int? axis = null,
bool keepdims = false,
string name = null)
参数:
- input_tensors: 输入的待降维的 tensor
- axis: 指定的轴,如果不指定,则计算所有元素的均值
- keepdims:是否降维度,默认 false。设置为 true,输出的结果保持输入tensor 的形状,设置为 false,输出结果会降低维度
- name: 操作的名称
tf.reduce_sum():用于计算张量 tensor 沿着指定的数轴(tensor 的某一维度)上的累加和,主要用作降维或者计算 tensor(图像)的累加和。
public Tensor reduce_sum(
Tensor[] input_tensors,
int? axis = null,
bool keepdims = false,
string name = null)
参数:
- input_tensors: 输入的待降维的 tensor
- axis: 指定的轴,如果不指定,则计算所有元素的累加和
- keepdims:是否降维度,默认 false。设置为 true,输出的结果保持输入 tensor 的形状,设置为 false,输出结果会降低维度
- name: 操作的名称
除此之外,还有一些常用的函数,例如 reduce_any、reduce_all、reduce_prod、reduce_max、reduce_min ,这些都实现了降维和统计运算的功能。
这些函数的参数列表也是基本相同的,其中第一项 input_tensors 为待运算和待降维的输入张量;第二项 axis 为降维的轴,即需要对其进行降维的轴;第三项 keepdims 设定输出张量的维度是否保持和输入张量一致,一般选默认 false 以实现降维的效果,如果有特殊需要输出维度保持不变的情况,可以设定为 true ;最后一项 name 定义操作的名称。
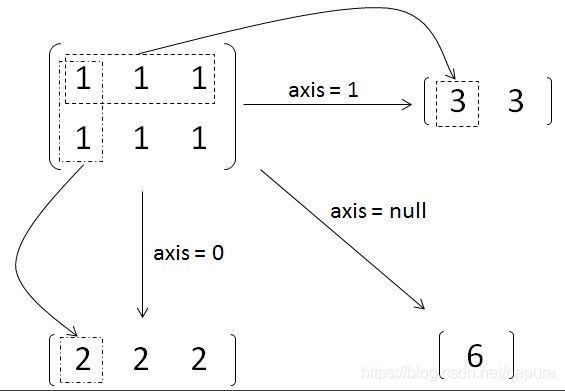
上面的参数列表中,第二项 axis 可能需要读者进行一下理解,特别是维度超过2维的情况。当 axis = 0 时,是纵向对矩阵求和,原来矩阵有几列最后就得到几个值;相似地,当 axis = 1 时,是横向对矩阵求和,原来矩阵有几行最后就得到几个值;当省略 axis 参数时,默认对矩阵所有元素进行求和,最后得到一个值。如下图所示:
对于一个多维的 array,最外层的括号里的元素的 axis 为 0,然后每减一层括号,axis 就加 1,直到最后的元素为单个数字。我们来按照3维的情况进行举例说明,例如 matrix = [[[1,2],[3,4]], [[5,6],[7,8]]]:
- axis=0时,所包含的元素有:[[1, 2],[3, 4]]、[[5, 6],[7, 8]]
- axis=1时,所包含的元素有:[1, 2]、[3, 4]、[5, 6]、[7, 8]
- axis=2时,所包含的的元素有:1、2、3、4、5、6、7、8
当 axis = 0,reduce_sum() 得到的结果应为 [[6 , 8], [10 , 12]],即把两个矩阵对应位置元素相加;当 axis = 1,reduce_sum() 得到的结果应为 [[ 4 , 6], [12 , 14]],即把数组对应元素相加。一句话总结就是对哪一维操作,计算完后外面的括号就去掉,相当于降维。
TF.NET 的 tf.reduce_mean 和 tf.reduce_sum 代码测试如下:
using NumSharp;
using System;
using Tensorflow;
using static Tensorflow.Binding;
namespace TF_Test
{
class Program
{
//Basic Operation tf.reduce_mean,tf.reduce_sum
static void Main(string[] args)
{
// 定义Tensor常量
var a = tf.constant(2);
var b = tf.constant(3);
var c = tf.constant(5);
// tf.reduce_mean 和 tf.reduce_sum 运算
var mean = tf.reduce_mean(new[] { a, b, c });
var sum = tf.reduce_sum(new[] { a, b, c });
// 访问运算结果并输出
print("mean =", mean.numpy());
print("sum =", sum.numpy());
}
}
}
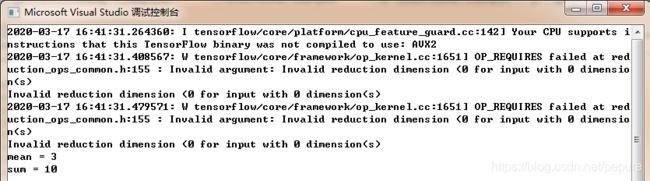
运行后,程序正确地输出了张量平均值与累加和的结果 3 和 10,如下所示:
5.5 Eager模式矩阵运算
最后,简单介绍一下Eager模式的矩阵运算,矩阵运算有 tf.diag()、tf.matmul()、tf.batch_matmul()等,这里主要说明下矩阵乘法 tf.matmul()。
矩阵乘法的运算公式是这样的,设 A 为 m × p 的矩阵, B 为 p × n 的矩阵,那么称 m ×n 的矩阵 C 为矩阵 A 与 B 的乘积,记作 C=AB ,其中矩阵 C 中的第 i 行第 j 列元素可以表示为:
如下所示:
简单地说,矩阵乘法就是矩阵A和矩阵B的行列交叉相乘并累加求和,求和的结果生成新的矩阵,如下图所示:
下面我们通过实际案例来说明,2个二维矩阵的乘法,我们先看一下公式:
然后我们通过代码实现一下2个二维矩阵的乘法,代码如下:
using NumSharp;
using System;
using Tensorflow;
using static Tensorflow.Binding;
namespace TF.Test
{
class Program
{
static void Main(string[] args)
{
// 矩阵乘法
var matrix1 = tf.constant(np.array(new float[,] { { 1, 2 }, { 3, 4 } }));
var matrix2 = tf.constant(np.array(new float[,] { { 5, 6 }, { 7, 8 } }));
var product = tf.matmul(matrix1, matrix2);
// 类型转换:tensor转换成numpy
print("product =", product.numpy());
}
}
}
通过代码调试我们可以看到 product 是一个 sharp 为[2,2] 的张量,各矩阵的形状如下:
程序运行后正确地输出了矩阵相乘的结果转换成的 numpy 类型数值为 [19, 22, 43, 50]:
C# TensorFlow 2 入门教程
Contact
GitHub
TensorFlow.NET: https://github.com/SciSharp/TensorFlow.NET
SciSharp-Stack-Examples: https://github.com/SciSharp/SciSharp-Stack-Examples
TensorFlow.NET-Tutorials: https://github.com/SciSharp/TensorFlow.NET-Tutorials