变分自编码器入门（Variational Auto Encoder, VAE）

1学习体会

如下图，我们假设头像图片的有三个特征$X=(x_1,x_2,x_3)$,（比如说$x_1$代表脸型，$x_2$代表眼睛，$x_3$代表嘴巴，这里选三个只是方便理解），确定值描述就是中间的坐标轴，每个特征都有确定的值；但在VAE中每个固定值是不存在的，而是以概率密度的形式存在。$X$为隐变量$Z$可能的值的一个。换而言之，$X$为隐变量$Z$在低维的映射。所谓道生一，一衍万物，不外如是。一组确定的值限制了我们的想象空间，通过隐函数的空间，大千变化才有了可能。以素描照片为底板，我们利用VAE可以生成不同眼睛、脸型和嘴巴的头像。

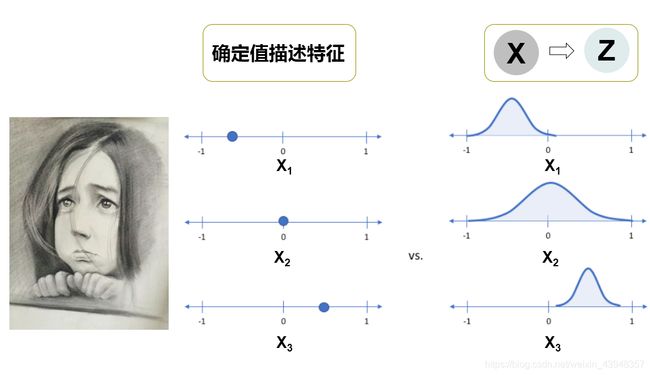
所谓隐函数参照这里。事实上我们只能看到$X$，$Z$是不可知的。不要慌，知道了$X$我们可以推求$Z$的概率,即$p\left(z|x\right)$。
$$p\left(z|x\right)=\frac{p\left(x|z\right)p\left(z\right)}{p\left(x\right)}$$
但是数学上求解$p\left(x\right)=\int p\left(x|z\right)p\left(z\right)dz$着实困难，因为对隐变量积分，尤其是高维的隐变量，大多数时候都是无法计算的^【2】。求积分的方法一种是利用蒙特卡洛求积分，另一种就是要用到叫变分的东西了。

2变分的意义

这里不细述变分的数学含义（我也不懂），而倾向于变分怎么在VAE中发挥作用。精确不行就逼近，定义一个函数$q\left(z|x\right)$无限逼近$p\left(z|x\right)$,如果我们可以定义q(z|x)的参数，使其非常类似于p(z|x)，那么上述的积分问题就可以迎刃而解了。$q\left(z|x\right)$也就是所谓变分分布。它应满足下面的条件，
$$\min KL\left(q\left(z|x\right)||p\left(z|x\right)\right)$$
其中，KL为KL散度，这个指标在熵理论中表述两个分布的接近程度，KL值越小,所谓的逼近就越成立，这也是我们VAE的一个约束条件。
言归正传，为了优化$ln(P(X))$的最大似然,【2】给出了两种推导方法来解释如何将观测值的对数似然转换成下式，
$$\max \underline{E_{q\left(z|x\right)}\log p\left(x|z\right)-KL\left(q\left(z|x\right)||p\left(z\right)\right)}$$
近一步转换为LOSS函数，
$$\mathcal{L}\left(x,\hat{x}\right)+\sum KL\left(q\left(z|x\right)||p\left(z\right)\right)\text{\hspace{1em}(∗)}$$
其中，第一项是给定隐变量时的条件分布的似然，第二项是变分分布和真实分布之间的KL散度。如果没有 KL 项，那VAE就等价于原始的AE模型。

3流程及存在的“对抗”

3.1流程

假设$x_1$，$x_2$，…，$x_i$的先验分布均服从正态分布$\mathcal{N}({\mu }_i,{\sigma }_i)$。那么$X$就可以用${\mu }_i$和${\sigma }_i$矢量化表示。但都默认$x_i$之间是独立不相关的，也就是说协方差只保存了对角线上的元素。这个假设一方面简化了计算，另一方面破坏了数据的结构，如各种相关性。下文先按简单的维度独立进行。

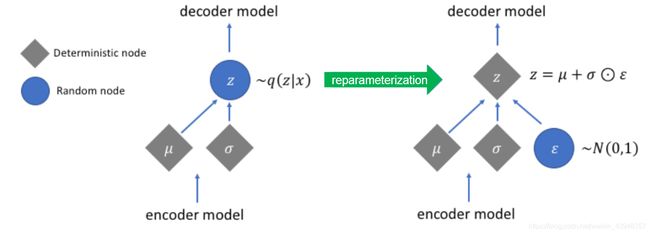
3.2Reparametrization

随机抽取参数以生成$x$有一个技巧，即抽样的再参数化技巧（Reparametrization）。从一个单位正态分布$\mathcal{N}(0,1)$中随机取样，然后通过潜在分布的平均值偏移来移动随机取样的平均值，并通过潜在分布的方差方差来缩放它。
$$z\sim q_{\theta }(z|x)=\mathcal{N}(z;{\mu }_{\theta }(x),{\sigma }_{\theta }(x))$$
等价于
$$z={\mu }_{\theta }(x)+{\sigma }_{\theta }(x)\cdot ϵ$$

3.3“对抗”

借助文献【4】，我们审视下不同条件约束下，即公式（$\ast$）不同项作为约束条件，隐空间$Z$的分布的结果。
如下图，左图只关注重建损失的意味着我们得到了与$X$一致的分布$\hat{X}$；空间中存在着大量空白，这不意外，因为$X$是$Z$低维空间的体现，我们的输出结果只是优化了条件分布（重复了输入）。
如果我们只关注于确保先验分布$p\left(z\right)$和潜在分布$q\left(z|x\right)$相似(公式（$\ast$）第二项，即KL散度损失项)，我们最终会使用相同的高斯分布来描述每一个观察结果，我们随后从该分布中采样来描述可视化的潜在维数。这不可避免将每一次观察都视为具有相同的特征;换句话说，我们没有描述原始数据。
只有公式（$\ast$）中的两项同时被优化时，如最右图，VAE才能描述一个观察的潜在状态，且分布接近先验，但在必要时偏离，从而保留了输入的显著特征。

由上述分析可知，公式（$\ast$）中的两项起的作用不同，一项以保存局部特征，另一项以保存整体分布。那么顺理成章之中，我们可以调节公式（$\ast$）的权重来匹配我们的目的。即Loss函数可进行如下转换。

加入权重$\beta$后，
$$\mathcal{L}\left(x,\hat{x}\right)+\beta \sum KL\left(q_j\left(z|x\right)||p\left(z\right)\right)$$

4改进

由于VAE的向量化输入导致数据的空间相关性缺失，参考文献【1】将一维的向量化输入整理成了一个矩阵输入，以保持图片行列像素之间的相关性，但潜在变量的先验仍然采用单一高斯函数描述。参考文献【5】采用了高斯混合模型的假设。

本文知识总结了对VAE的一些粗浅认知，对于如何应用尚未实操，不足之处，恳请多多指正。

5参考文献

【1】A, J. L. , A, H. Y. , B, J. G. , A, D. K. , A, L. W. , & A, S. W. , et al. (0). Matrix-variate variational auto-encoder with applications to image process. Journal of Visual Communication and Image Representation, 67.
【2】https://zhuanlan.zhihu.com/p/57574493
【3】https://wizardkingz.github.io/VAE/
【4】https://www.jeremyjordan.me/variational-autoencoders/
【5】https://openaccess.thecvf.com/content_ICCV_2019/papers/Yang_Deep_Clustering_by_Gaussian_Mixture_Variational_Autoencoders_With_Graph_Embedding_ICCV_2019_paper.pdf