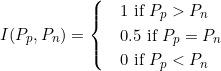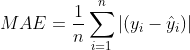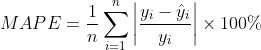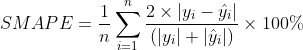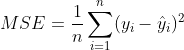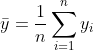机器学习中准确率、精确率、召回率、误报率、漏报率、F1-Score、AP&mAP、AUC、MAE、MAPE、MSE、RMSE、R-Squared等指标的定义和说明

在机器学习和深度学习用于异常检测（Anomaly detection）、电子商务（E-commerce）、信息检索（Information retrieval, IR）等领域任务（Task）中，有很多的指标来判断机器学习和深度学习效果的好坏。这些指标有相互权衡的，有相互背向的，所以往往需要根据实际的任务和场景来选择衡量指标。本篇博文对这些指标进行一个梳理。

一、名称解释

1、真实值actual value和预测值predicted value

这两者就是字面的意思，actual value是指真实记录的已发生的测量结果值，而predicted value是指对未发生的预测值。这里的值既可以是数值型，也可以是类别型。

2、真True、假False

这两个表示的是真实值与预测值之间是否吻合，true表示的是预测值与真实值一致，而false表示的是预测值与真实值不一致。

3、阳性Positive（正）、阴性Negative（负）

首先这里讨论的positive和negative不代表性别的取向，同时正和负也不代表正确或者错误。positive指条件或者事物存在，而negative指条件或者事物不存在。例如异常检测领域阳性positive代表存在异常，阴性negative代表不存在异常；如健康领域阳性positive代表检测存在病毒或者疾病，阴性negative代表检测结果是健康的。再如电子商务领域阳性positive代表点击或者成交，阴性negative代表未点击或者未成交。

4、曝光List、点击Click、加收藏Wish/加关注Follow、加购Cart、订单Order、支付Pay

这几项名称往往用于网络内容或者电商领域，代表的是一则内容或者一个商品从展现给用户到用户消费该内容或者商品的过程。含义就是由字面代表的意思。

二、分类指标的定义和说明（准确率、精确率、召回率、误报率、漏报率）

首先看下面这张图，里面对部分指标做了定义。接下来对各个指标的定义和说明进行阐述：

如上图，将样例（样本，后面两者混用）分为阳性（正，后面两者混用）样例和阴性（负，后面两者混用）样例，将正样本预测为正样本的为True positive（），正样本预测为负样本的为False negative（），负样本预测为正样本的为False positive（），负样本预测为负样本的为True negative（）。所以有，。

1、准（正）确率accuracy

反映分类器或者模型对整体样本判断正确的能力，即能将阳性（正）样本positive判定为positive和阴性（负）样本negative判定为negative的正确分类能力。值越大，性能performance越好

这里注意，在负样本占绝对多数的场景中，不能单纯追求准确率，因为将所有样本都判定为负样本，这种情况下准确率也是非常高的。

2、精确率precision

反映分类器或者模型正确预测正样本精度的能力，即预测的正样本中有多少是真实的正样本。值越大，性能performance越好

这里注意，单纯追求精确率，会造成分类器或者模型少预测为正样本，这时低，即精确率就会很高。

3、召回率recall，也称为真阳率、命中率（hit rate）

反映分类器或者模型正确预测正样本全度的能力，增加将正样本预测为正样本，即正样本被预测为正样本占总的正样本的比例。值越大，性能performance越好

这里注意，单纯追求召回率，会造成分类器或者模型基本都预测为正样本，这时低，即召回率就会很高。

4、误报率false alarm，也称为假阳率、虚警率、误检率

反映分类器或者模型正确预测正样本纯度的能力，减少将负样本预测为正样本，即负样本被预测为正样本占总的负样本的比例。值越小，性能performance越好

5、漏报率miss rate，也称为漏警率、漏检率

反映分类器或者模型正确预测负样本纯度的能力，减少将正样本预测为负样本，即正样本被预测为负样本占总的正样本的比例。值越小，性能performance越好

6、特异度specificity

反映分类器或者模型正确预测负样本全度的能力，增加将负样本预测为负样本，即负样本被预测为负样本占总的负样本的比例。值越大，性能performance越好

三、分类指标间的关系

由上述指标的定义，可以得到如下的一些指标间的关系：

，即召回率+漏报率=1

，即特异性+误报率=1

四、分类综合指标（F1-Score、AP&mAP、AUC）

1、F1-Score

首先看下F值，该值是精确率precision和召回率recall的加权调和平均。值越大，性能performance越好。F值可以平衡precision少预测为正样本和recall基本都预测为正样本的单维度指标缺陷。计算公式如下：

常用的是F1-Score，即a=1，所以上述公式转化为：

2、AP&mAP

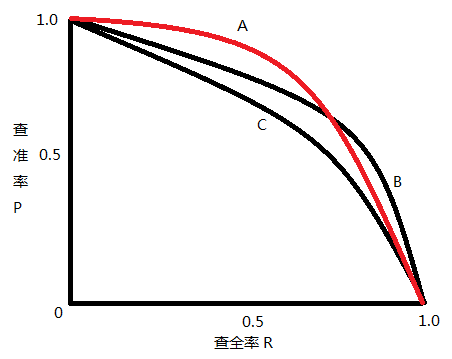
AP表示precision-recall曲线下的面积，mAP是mean average precision的简称，是各类别AP的平均值。

面积求积分一般转为离散的矩形面积计算，如上图下边图形所示。计算公式如下：

3、AUC

一般选取一个特定阀值（threshold），预测为正样本的概率大于等于该阀值判定为正样本，小于该阀值判定为负样本。根据上面描述的公式得到召回率TPR和误报率FPR，在平面上描述对应的坐标点和值，就得到如下的ROC曲线，其中TPR为纵轴，FPR为横轴。

ROC曲线里，左下角（0, 0）阀值是最大的，此时所有样本都判定为负样本，所以有

，

，

，

.

右上角（1, 1）阀值是最小的，此时所有样本都判定为正样本，所以有

，

，

，

.

那么从左下角到右上角移动过程中，随着阀值的逐渐减小，越来越多的正样本会被判定为正样本，但也伴随着负样本被判定为正样本。所以TPR和FPR都会增大。当然最佳的阀值是越接近左上角，和，TPR大于FPR的最大概率。

而ROC曲线向下覆盖的面积（上图中浅绿部分）即为AUC值。AUC取值为[0, 1]，值越大，性能performance越好。假设随机挑选一个正样本和一个负样本，分类器或者模型计算得到相应的分值score。如果AUC值越大，那么根据计算分值将样本排序后，实际上排在前面的样本是正样本的概率也是越大（就是分类器或者模型输出正样本为正的比输出负样本为正要大的概率，即AUC值）。AUC值的计算有好几种方法：

1）、按定义计算ROC曲线下的面积

2）、

其中，为正样本的数量，为负样本的数量，为一个正样本与一个负样本的样本对的数量。按计算分值score从小到大排序，分值最大score对应的样本的，第二大分值score对应的样本的，依次类推。如果计算分值score相等，则相等得分的rank取平均值。该计算方法也是以下计算方法的扩展：

正样本的预测概率大于负样本的预测概率的个数/一个正样本与一个负样本的样本对的数量

，

其中：

.

假设有如下4个样本，其中1个正样本，3个负样本：

ID	Label	probability score
A	0	0.2
B	0	0.5
C	1	0.7
D	0	0.7

 

所以，。此时

.

AUC的计算方法已经同时考虑了分类器或者模型对于正样本和负样本的分类能力。所以即使训练样本存在不平衡，AUC指标依然能对分类器或者模型作出合理的评价。

五、回归指标的定义和说明（MAE、MSE、RMSE、R-Squared）

这里的回归指回归问题和模型，如线性回归Linear Regression，决策树Decision Tree Regression，随机森林Random Forest Regression，深度学习RNN等等。

1、平均绝对误差mean absolute error（MAE）

使用的是数据的偏差的绝对值，计算公式如下：

，

其中为真实值，为回归预测值，为回归的数据个数。值越小，性能performance越好

这里注意，绝对值的计算因为不是处处可导，不方便用来当求极值的目标。

2、平均绝对百分比误差mean absolute percentage error（MAPE）

将MAE的绝对值转化为相对值，计算公式如下：

，

其中为真实值，为回归预测值，为回归的数据个数。注意由于这里用了作为分母，所以当测量真实值有数据为0时，即存在分母为0的情况，该指标公式就不可用了。值越小，性能performance越好

3、对称平均绝对百分比误差symmetric mean absolute percentage error（SMAPE）

将MAE的绝对值转化为相对值，分母使用真实值和预测值的平均值，计算公式如下：

，

其中为真实值，为回归预测值，为回归的数据个数。SMAPE区别MAPE的是分母由改为和的平均值。同样地，由于这里用了作为分母，所以当测量真实值加预测值有数据为0时，即存在分母为0的情况，该指标公式就不可用了。值越小，性能performance越好

4、均方误差mean squared error（MSE）

使用的是数据的偏差的平方和，计算公式如下：

，

其中为真实值，为回归预测值，为回归的数据个数。注意该公式也用于回归的损失函数，并且可导（MAE绝对值不是处处可导的），即最小化均方误差。值越小，性能performance越好

5、均方根误差root mean squared error（RMSE）

使用的是数据的偏差的平方和再求根号，计算公式如下：

，

其中为真实值，为回归预测值，为回归的数据个数。其实是均方误差MSE开根号得到的，实质跟均方误差MSE是一样的。主要用于降低均方误差的数量级，防止均方误差MSE看起来很大。RMSE和MAE的数量级基本相同了，但RMSE会比MAE大一些，RMSE惩罚了预测误差大的数据点。关于用RMSE还是MAE，有比较多的讨论（Willmott et al., 2005, 2009）、（Chai, 2014），跟使用场景的数据分布等相关。当然求得的回归曲线RMSE值越小，反映求得曲线的最大误差也是较小的。所以RMSE值越小，性能performance越好

6、R方R Squared

因为MAE、MSE、RMSE的衡量不存在一个区间范围，所以定义了R方这个指标，计算公式如下：

，

，

其中为真实值，为回归预测值，为真实值的平均值，为回归的数据个数。表示残差的平方和（residual sum of squares，即模型的预测误差的平方和），表示预测值都为的残差的平方和（total sum of squares）。取值范围，表示预测模型在每一个测量数据上都预测完全正确，表示等价于平均值预测法，表示预测模型比平均值预测法还差。值越大，性能performance越好

六、场景相关说明

为什么要定义这么多指标，准确率和精确率不看公式定义，还容易弄混。这是因为不同的场景强调不同的分类能力，例如有的场景不希望正样本漏掉，有的场景不希望误报。所以机器学习和模式识别得到的分类器或者模型，就需要有不同的指标了。

1、异常检测

异常检测是一个非常追求召回率，同时也强调准确率的领域（如准确率>85%，召回率>99%）。那么召回率是否一定要做到100%呢？这要看成本与召回率提升所带来的收益了。举个例子，金融银行的信用卡申请欺诈。金融银行A收到10,0000份信用卡的申请，其中有100份是欺诈的，检测出99份的欺诈申请了，其余的被判定是无欺诈的。所以召回率为：

，

准确率为：

，

此时是否必须要等另一份欺诈申请检测出来才能发放信用卡呢，应该是金融系统会评估这一份“欺诈申请”带来的损失（如额度10000元的损失）是否小于通过“其他无欺诈信用卡申请”带来的收益。

2、电子商务

举个例子，电商广告100个投放，其中用户会点击的正样本为1个，其余为用户不点击的负样本（不平衡数据集）。如果分类器简单地将样本都分为负样本，准确率为

，

准确率非常高，但显然没有意义。这些场景里分类器会追求广告转化过程中的指标，如对应曝光指标的有：

1）千次曝光费用cost-per-mille（cpm=一千次曝光的费用），

2）单位时间费用cost-per-time（cpt=单位时间的费用），

3）每天费用cost-per-day（cpd=一天的费用）。

对应点击指标的有：

1）点击通过率click-through-rate（点击率ctr=投放广告被点击的次数/广告总的曝光次数），

2）每次点击费用cost-per-click（cpc=一定时间内总费用/广告总的点击次数）。

对应转化指标的有：

1）转化率conversion-rate（cvr=投放广告的转化次数/广告的点击次数），这里的转化可以是商品购买、应用app下载、注册、地产推广用户登记报名等，

2）每次行为费用cost-per-action（cpa=一定时间内总费用/广告总的行为次数），这里行为可以是下载、注册、用户登记报名等，一般不付费，

3）每次下载费用cost-per-download（cpd=一定时间内总费用/广告产生的下载量），

4）每次安装费用cost-per-install（cpi=一定时间内总费用/广告产生的安装量），

5）每次购买费用cost-per-sales（cps=一定时间内总费用/广告产生的销售量），这里是购物类的商品产生了具体的销售。

对应成本核算指标的有：

1）投资回报率return-on-investment（ROI=广告产生价值/广告总的费用），这里广告产生价值可以是广告产生利润、广告产生销售额等

3、信息检索

信息检索是一个同时追求召回率recall和精确率precision的领域，即mAP指标（Tan et al., 2006）。另外还有指标TopN的精确率（Pr@N=topN中的点击数/N）用来衡量在曝光有限情况下的效果，因为人们浏览检索结果的页数与数量是有限的。常用的如：

，

其他的根据用户平均能浏览的深度，如10个，还有Pr@10等指标。

4、化工故障检测

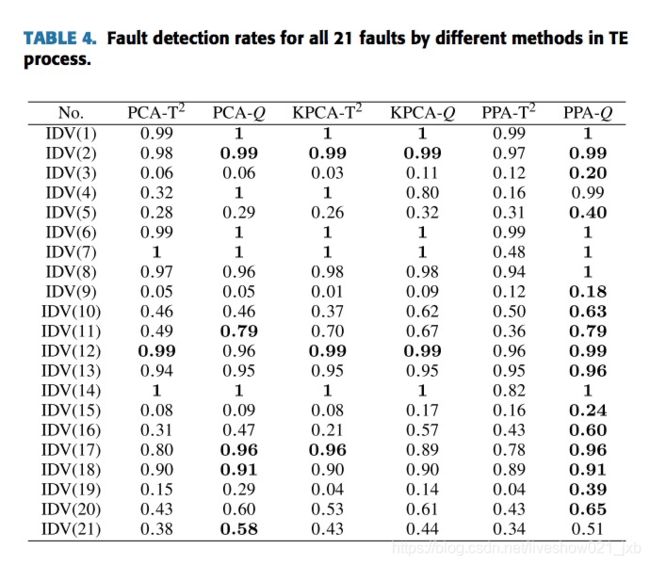
在化工故障检测领域中，用故障检测率fault detection rate（即召回率recall）和误报率false alarm rate来反映效果的好坏。当故障细化到某一个具体的类别时，有故障A1的故障检测率：

，

如上表中（Zhang et al., 2018），21个故障类别的故障检测率。如果不标记具体类别，指的是平均故障检测率（mean fault detection rate），即各个故障类别检测率的平均值。

5、信号分析

举个例子，军舰雷达收到100个水雷来袭的信号，其中真正的水雷来袭信号为3个，其余97个是迷惑性的敌方模拟信号。假如分类器将2个真正的水雷来袭信号判定为正样本，其余98个信号判定为负样本（1个正样本+97个负样本）。这种情况下，准确率：

，

精确率：

，

可以看到准确率和精确率都非常高，我们再计算下其他指标，召回率：

，

误报率：

，

漏报率：

.

可以看到误报率为0，非常好。但漏报率很高，这漏掉的水雷可能造成军舰沉没。所以这个场景里，漏报是致命的。那反过来说，把漏报率做成0，分类器简单地把所有信号都判定为正样本，实现非常简单，是不是就是最好的？显然不是，一般收到警报是要动员，准备应对和反击的，如果误报率很高，不停的动员，最后大家都累死了，也容易造成“狼来了”的漠视态度。所以这个场景里分类器要追求漏报率为0，但误报率也要控制在很小的范围内。

引用

【1】Wikipedia：Sensitivity and specificity

【2】http://en.wikipedia.org/wiki/Precision_and_recall

【3】http://en.wikipedia.org/wiki/Accuracy_and_precision

【4】T. Fawcett. An introduction to ROC analysis. Pattern Recognition Letters. 27(8): 861–874, 2006

【5】C. Willmott, and K. Matsuura. Advantages of the Mean Abso-lute Error (MAE) over the Root Mean Square Error (RMSE) in assessing average model performance. Clim. Res., 30, 79–82, 2005

【6】C. J. Willmott, K. Matsuura, and S. M. Robeson. Ambiguities inherent in sums-of-squares-based error statistics. Atmos. Env-iron., 43, 749–752, 2009

【7】T. Chai. Root mean square error (RMSE) or mean absolute error (MAE). Geoscientific Model Development discussions. 7(1), 1247-1250, 2014

【8】B. Tan, X. Shen, and C. Zhai. Mining long-term search history to improve search accuracy. Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. Pages 718-723, 2006

【9】X. Zhang, M. Kano, and Y. Li. Principal Polynomial Analysis for Fault Detection and Diagnosis of Industrial Processes. IEEE Access. vol. 6, 52298-52307, 2018