K近邻算法理论和代码实现

一、k-近邻算法理论

1.k-近邻算法的基本原理

对于未知类别属性数据集中的点：
（1）计算已知类别数据集中的每个点与当前点之间的距离；使用欧式距离公式，计算两个向量点x1和x2之间的距离公式如下：

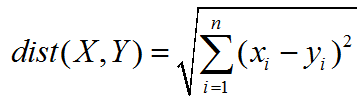
（2）按照距离递增次序排序；
（3）选取与当前点距离最小的k个点；
（4）确定前k个点所在类别的出现频率；
（5）返回前k个点出现频率最高的类别作为当前点的预测分类。

2.k-近邻算法的三要素

k值的选择、距离度量、分类决策规则

3.k-近邻算法的评价

优点
（1）k-近邻算法是分类数据最简单最有效的算法，它是一种lazy-learning算法；
（2）分类器不需要使用训练集进行训练，训练时间复杂度为0。
缺点
（1）计算复杂度高、空间复杂度高：kNN分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为n，那么kNN的分类时间复杂度为O(n)；
（2）耗内存：必须保存全部的数据集，如果训练数据集很大，必须使用大量的存储空间；
（3）耗时间：必须 对数据集中的每一个数据计算距离值，实际使用时可能非常耗时；
（4）无法给出任何数据的基础结构信息（数据的内在含义），这是k-近邻算法最大的缺点。

4.k-近邻算法的问题及解决方案

问题1：当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的k个邻居中大容量类的样本占多数。
解决：不同样本给予不同的权重项

问题2：数字差值最大的属性对计算结果的影响最大
解决：在处理不同取值范围的特征值时，通常采用的方法是将数值归一化，如将取值范围处理为0到1或者-1到1之间。

二、k-近邻算法代码实现

1.k-近邻算法代码组成

kNN.py

'''
kNN: k Nearest Neighbors
Input:      inX: vector to compare to existing dataset (1xN)
            dataSet: size m data set of known vectors (NxM)
            labels: data set labels (1xM vector)
            k: number of neighbors to use for comparison (should be an odd number)         
Output:     the most popular class label
@author: pbharrin
'''
from numpy import *
import operator
from os import listdir
import pandas as pd
import numpy as np

def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX, (dataSetSize,1)) - dataSet
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort()     
    classCount={
     }          
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]


def file2matrix(filename,feature_num):
    df = pd.read_excel(filename)
    df = df.reindex(np.random.permutation(df.index))
    df.to_excel('random.xlsx')
    df_values = df.values
    returnMat = df_values[:,:feature_num]
    classLabelVector = df_values[:,-1]
    return returnMat,classLabelVector
    
def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m,1))
    normDataSet = normDataSet/tile(ranges, (m,1))   #element wise divide
    return normDataSet, ranges, minVals
   
def datingClassTest(filename,feature_num):
    hoRatio = 0.10      #hold out 10%
    returnMat,classLabelVector = file2matrix(filename,feature_num)    #load data setfrom file
    normMat, ranges, minVals = autoNorm(returnMat)
    m = normMat.shape[0]
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],classLabelVector[numTestVecs:m],3)
        print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, classLabelVector[i]))
        if (classifierResult != classLabelVector[i]): errorCount += 1.0
    print ("the total error rate is: %f" % (errorCount/float(numTestVecs)))
    print (errorCount)
    
def classifyPerson(filename,feature_num):
    resultList = ['No','Yes']
    feature0 = float(input("your feature0："))
    feature1 = float(input("your feature1："))
    feature2 = float(input("your feature2："))
    returnMat,classLabelVector = file2matrix(filename,feature_num)
    normMat, ranges, minVals = autoNorm(returnMat)
    inArr = array([feature0, feature1, feature2])
    classifierResult = classify0((inArr-minVals)/ranges,normMat,classLabelVector,3)
    print("Result: ",resultList[classifierResult])

2.k-近邻算法代码完成运用

import pandas as pd
import numpy as np
%matplotlib inline
%matplotlib notebook
import matplotlib.pyplot as plt
from numpy import *
import numpy as np

2.1引入kNN.py

# 引入kNN.py
import kNN
filename='EN20200923_np.xlsx'
feature_num=3
returnMat,classLabelVector = kNN.file2matrix(filename,feature_num)
returnMat
#array([[  1,   2, 255],
#       [  2,   3, 500],
#       [  3,   2, 410],
#       ...,
#       [  2,   3, 640],
#       [  3,   3, 795],
#       [  2,   1, 455]], dtype=int64)

classLabelVector
#array([1, 1, 1, ..., 1, 1, 1], dtype=int64)

2.2 准备数据：归一化数据

normMat, ranges, minVals = kNN.autoNorm(returnMat)
normMat
#array([[0.        , 0.33333333, 0.26153846],
#       [0.25      , 0.66666667, 0.51282051],
#       [0.5       , 0.33333333, 0.42051282],
#       ...,
#       [0.25      , 0.66666667, 0.65641026],
#       [0.5       , 0.66666667, 0.81538462],
#       [0.25      , 0.        , 0.46666667]])

ranges
#array([  4,   3, 975], dtype=int64)

minVals
#array([1, 1, 0], dtype=int64)

2.3 分析数据：使用matplotlib

import matplotlib.pyplot as plt
import matplotlib
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(normMat[:,1],normMat[:,2],s=15.0*array(classLabelVector),c=15.0*array(classLabelVector))
plt.show()

2.4 测试算法：作为完整程序验证分类器

kNN.datingClassTest(filename,feature_num)
#the classifier came back with: 1, the real answer is: 1
#the classifier came back with: 1, the real answer is: 1
#the classifier came back with: 1, the real answer is: 1
#the classifier came back with: 1, the real answer is: 1
#the total error rate is: 0.007194
#3.0

2.5 使用算法：构建完整可用系统

kNN.classifyPerson(filename,feature_num)

#your feature0：3
#your feature1：1
#your feature2：230
#Result:  No