hslogic_基于迫零准则的自适应线性均衡器

在数字通信系统中，码间串扰和加性噪声是造成信号传输失真的主要因素，为克服码间串扰，在接收滤波器和抽样判决器之间附加一个可调滤波器，用以校正(或补偿)这些失真。对系统中线性失真进行校正的过程称为均衡，实现均衡的滤波器称为均衡滤波器。

由于信道特性是变化的，均衡器的参数也应该随之而改变，可以自动调整参数以保持最佳工作状态的均衡器就是自适应均衡器(自适应滤波器)。自适应均衡器有频域均衡和时域均衡之分。频域均衡器只能均衡时变信道的幅频特性，不能有效地均衡群时延特性，在数字信号中一般不采用。时域均衡器利用它所产生的响应去补偿已畸变的信号波形，可以有效地抑制码间串扰和加性干扰。随着数字信号处理理论和超大规模集成电路技术的发展，时域均衡已广泛应用于数字通信的各个领域。

接收端的码间干扰(ISI)，使系统误码率上升，严重情况下使系统无法继续正常工作。理论和实践证明，在接收系统中插入一种滤波器，可以校正和补偿系统特性，减少码间干扰的影响。这种起补偿作用的滤波器称为均衡器。

随着数字信号处理理论和超大规模集成电路的发展，时域均衡已成为当今高速数字通信中所使用的主要方法。调整滤波器抽头系数的方法有手动调整和自动调整。如果接收端知道信道特性，例如信道冲击响应或频域响应，一般采用比较简单的手动调整方式。由于无线通信信道具有随机性和时变性，即信道特性事先是未知的，信道响应是时变的，这就要求均衡器必须能够实时地跟踪通信信道的时变特性，可以根据信道响应自动调整抽头系数，我们称这种可以自动调整滤波器抽头系数的均衡器为自适应均衡器。

1.2 国内外研究性现状

均衡技术最早应用于电话信道，由于电话信道频率特性不平坦和相位的非线性引起时间的弥散，使用加载线圈的均衡方法来改进传送语音用的双绞线电缆的特性。在高速数字移动通信、数字微波无线通信系统和作为重要的远程通信和军事通信手段之一的短波通信系统中, 由于多径与衰落现象引起码间干扰,系统性能恶化。采用适当有效的自适应均衡技术, 可以克服数据传输在频带利用率、误码率性能以及传输速率上的许多缺点。

自适应均衡就是通过接收端的均衡器产生与信道特性相反的特性以抵消信道时变多径传播引起的干扰，可消除波形叠加、码间串扰，也能减小加性噪声干扰，从而减小误码的技术。均衡分为频域均衡和时域均衡。频域均衡指总的传输函数满足无失真传输的条件。时域均衡是使总冲击响应满足无码间干扰的条件。在实际电路中，往往同时采用频域和时域自适应均衡器，最大限度地提高电路的抗衰落能力。

均衡技术最早应用于电话信道，由于电话信道频率特性不平坦和相位的非线性引起时间的弥散，使用加载线圈的均衡方法来改进传送语音用的双绞线电缆的特性。上世纪六十年代以前，均衡器的参数是固定的或手调的，其性能很差。1965年，出现了一种“迫零自适应均衡器”。1965年DiToro独立把自适应均衡器应用于对抗码间干扰对高频链路数据传输的影响。1967年，Austin提出了判决——反馈均衡器。1969年，Gersho以及Proakis和Mi1le使用最小均方误差准则独立的重新描述了自适应均衡器问题。1972年，Ungerboeck对采用自适应最小均方误差算法的均衡器的收敛性进行了详细的分析。1978年，Falconer和Ljung介绍了快速卡尔曼算法的一种修正，从而将其计算复杂性简化到可与简单的LMS算法比较的程度。Satorius和Alexander在1979年、Satorius和Pack在1981年证明了色散信道格型自适应均衡器算法的实用性。

1.3基于MATLAB仿真概要

在MATLAB通信工具箱中有SLMULINK仿真模块和MATLAB函数，形成一个运算函数和仿真模块的集合体，用来进行通信领域的研究、开发、系统设计和仿真。通信工具箱中的模块可供直接使用，并允许修改，使用起来十分方便，因而完全可以满足使用者设计和运算的需要。

    MATLAB通信工具箱中的系统仿真，分为用SIMULINK模块框图进行仿真和用MATLAB函数进行的仿真两种。在用SIMULINK模块框图的仿真中，每个模块，在每个时间步长上执行一次，就是说，所有的模块在每个时间步长上同时执行。这种仿真被称为时间流的仿真。而在用MATLAB函数的仿真中，函数按照数据流的顺序依次执行，意味着所处理的数据，首先要经过一个运算阶段，然后再激活下一个阶段，这种仿真被称为数据流仿真。某些特定的应用会要求采用两种仿真方式中的一种，但无论是哪种，仿真的结果是相同的。

下面我们将通过中频调制进行仿真验证，并研究多阶迫零算法的性能对比。本章的第二节，我们已经介绍了系统的抗ISI能力，并对其误码率做了分析，下面我们将进行调制，然后分析在中频条件下，不同的阶数的迫零算法的误码率已经星座图分析。

    整个系统的主程序如下所示：

x=randint(N,1);                    

yy=reshape(x,k,length(x)/k)';

xsym=bi2de(reshape(x,k,length(x)/k)');

x1=modulate(modem.qammod(M),xsym);

x2 = conv(x1,h);

x3 = AWGN(x2,SNR,'measured','linear'); 

x6 = conv(x3,cc);   

下面我们将从星座图来分析迫零均衡的主要效果：

这里我们假设在相同的SNR下进行测试，分别测试1，2，5，7阶数的迫零均衡器的功能。

 

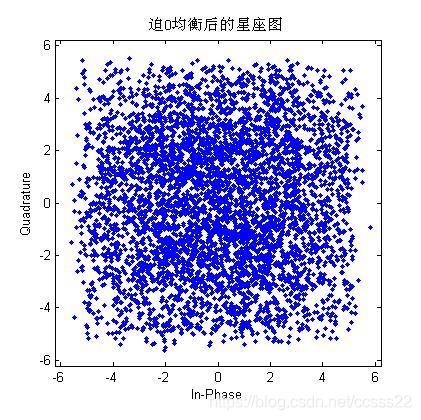
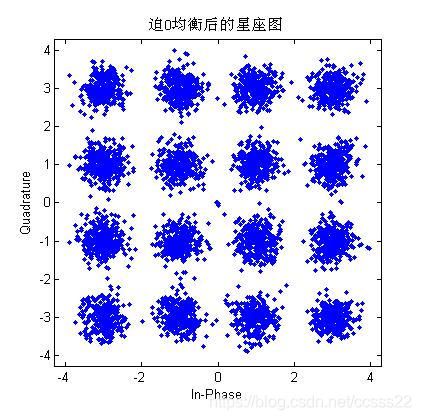
·1阶滤波器

   

图3-6 通过1阶迫零均衡器前后星座图对比

     当仅通过1阶迫零均衡器后，系统的性能并没有得到有效的改善，这说明，在实际工作中，我们需要更高阶的迫零均衡器。

·2阶滤波器

图3-7 通过3阶迫零均衡器前后星座图对比

·5阶滤波器

图3-8 通过5阶迫零均衡器前后星座图对比

·7阶滤波器

图3-9 通过7阶迫零均衡器前后星座图对比

    从上面的结果分析可见，我们可以看到在一阶迫零的情况下，系统性能较差，在多阶迫

零均衡器后，系统的性能较好。基本能够得到标准的星座图信号，点基本在预定的位置的小范围内晃动，符合系统的设计要求。当阶数较高的时候，系统基本星座图基本达到相似的效果，这说明，在实际工作中，我们一般只要设计一定阶数的迫零均衡器就可以了。并不需要将阶数设计的很高。下面我们来通过误码率来分析不同阶数的系统误码率。

    下面我们来看看系统的误码率分析：

图3-10 1，2，5，7阶迫零算法的误码率分析

    同上面星座图和误码率曲线的分析，我们基本可以知道，系统在1阶迫零的情况下，性能较差，无法正常的工作，此时其误码率也非常的高，当阶数增加到2阶的时候，系统的性能得到了明显的 改善，当系统阶数更高的时候，系统效果良好，误码率很低，基本达到应用级别。

    从这里我们可以看到，在实际工作中，我们一般采用5阶迫零均衡器就可以了。这样即有利于系统的设计实现，也节约了大量的硬件资源。