树、二叉树、查找算法总结

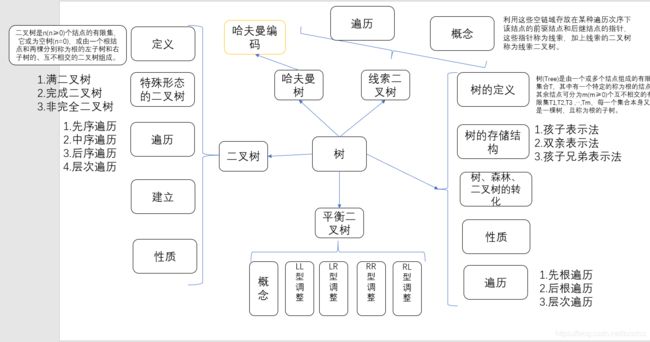
树、二叉树、查找算法总结

---

前言

在经过了对树、二叉树、查找算法的学习之后，我对于这些知识也有了一定的了解，这一章的知识面与前面的章节相比，显得庞大了许多，原因在于树的复杂性以及变化的丰富度是线性表所不能相比的。于是我便记录了一下这些概念及联系。

以下为我画的思维导图：

一、树

1.树的定义

树(Tree)是由一个或多个结点组成的有限集合T，其中有一个特定的称为根的结点；其余结点可分为m(m≥0)个互不相交的有限集T1,T2,T3 ,…,Tm，每一个集合本身又是一棵树，且称为根的子树。

树的基本术语有结点的度与树的度，分支结点与叶子结点，路径与路径长度，孩子节点、双亲结点和兄弟结点，结点层次和树的高度，有序树和无序树，森林等。

一般树与二叉树的区别：

1.树的结点个数至少为1，而二叉树的结点个数可以为0；
2.树的结点最大度数没有限制，而二叉树结点的最大度数为2；
3.树的结点无左、右之分，而二叉树的结点有左、右之分。

2.树的存储结构

孩子表示法：用指针指出每个节点的孩子节点

其结构体定义为：

typedef struct CTNode {
     
	int child;
	struct CTNode* next;
}*ChildPtr;
typedef struct {
     
	TElemType data;
	ChildPtr firstchild;
}CTBox;
typedef struct {
     
	CTBox nodes[MAXS];
	int r, n;
}CTree;

双亲表示法：用指针表示出每个节点的双亲节点

其结构体定义为：

typedef struct PTNode {
     
	TElemType data;
	int parent;
}PTNode;
typedef struct {
     
	PTNode nodes[10000];
	int r, n;
}PTree;

孩子兄弟表示法：即表示出每个节点的第一个孩子节点，也表示出每个节点的下一个兄弟节点

其结构体定义为：

typedef struct CSNode {
     
	TElemType data;
	struct CSNode* firstchild, * rightsib;
}CSNode,*CSTree;

三.树，森林，二叉树的转化

二、二叉树

1.定义

二叉树是n(n≥0)个结点的有限集，它或为空树(n=0)，或由一个根结点和两棵分别称为根的左子树和右子树的、互不相交的二叉树组成。

其结构体定义为：

typedef struct node {
     
	ElemType data;
	struct node* lchild;
	struct node* rchild;
}BTNode;

二叉树分为3种:

二叉树有如下性质
1.非空二叉树上的叶子结点数等于双分支结点数加1。
2.非空二叉树的第i层上最多有2^(i-1)个结点（i≥1）
3.高度为h的二叉树最多有2^h-1个结点（h≥1）
二叉树的存储方式分为顺序存储和链式存储两种方式：
顺序存储：


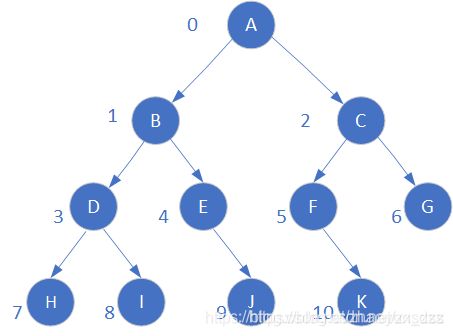
优点：适合完全二叉树和满二叉树，序号可以反映出结点之间的逻辑关系，可以节省空间
缺点：适合一般二叉树，只能添加一些空结点，空间利用率低
链式存储结构：

二叉树每个结点最多两个孩子，所以设计二叉树的结点结构时考虑两个指针指向该结点的两个孩子。

2.拥有特殊形态的二叉树

斜树:每个结点只有左结点或者每个结点只有右结点

满二叉树:树种每一层都含有最多的结点，对于编号i的结点，期双亲结点为⌊ i / 2 ⌋

完全二叉树：每一个结点都与高度为h的满二叉树编号1 − n相同；如果i ≤ n / 2下，则结点i为分支结点，否则为叶子结点

二叉排序树：左子树均小于根结点，右子树均大于根结点

平衡二叉树：左右子树的深度之差不超过1

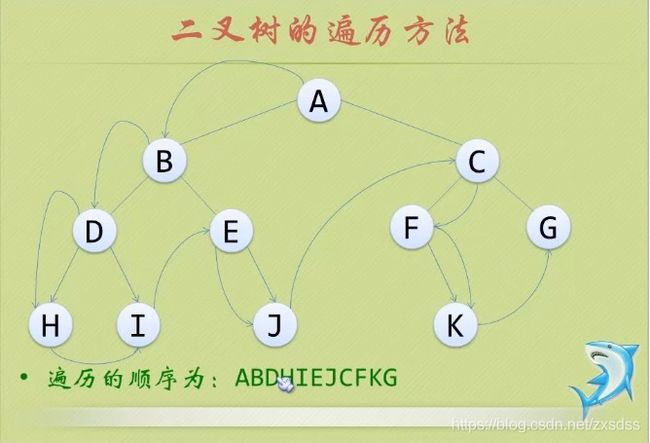
三.二叉树的遍历

1.先序遍历

若树为空，则空操作返回。否则，先访问根节点，然后前序遍历左子树，再前序遍历右子树。

void PreOrder(BTNode* b)
{
     
	if (b != NULL) {
     
		cout << b->data;
		PreOrder(b->lchild);
		Preorder(b->rchild);
	}
}

2.中序遍历

若树为空，则空操作返回。否则，从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后是访问根节点，最后中序遍历根节点的右子树。

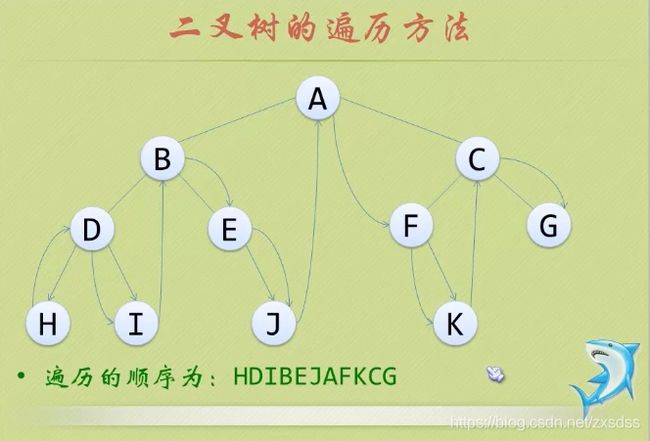
void InOrder(BTNode* b)
{
     
	if (b != NULL) {
     
		InOrder(b->lchild);
		cout << b->data;
		Inorder(b->rchild);
	}
}

3.后序遍历

若树为空，则空操作返回。否则，从左到右先叶子后节点的方式遍历访问左右子树，最后访问根节点。

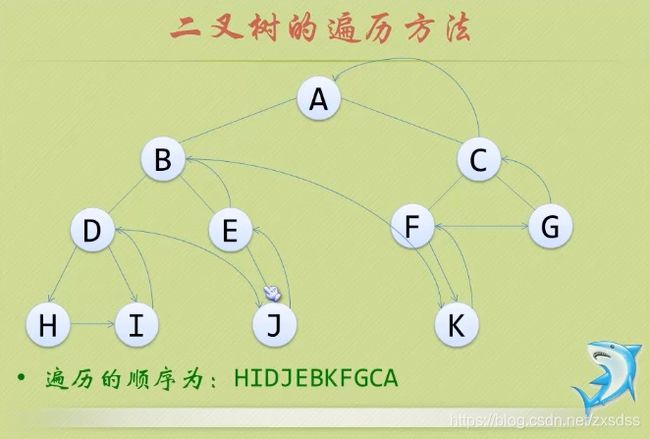
void PostOrder(BTNode* b)
{
     
	if (b != NULL) {
     
		PostOrder(b->lchild);
		PostOrder(b->rchild);
		cout << b->data;
	}
}

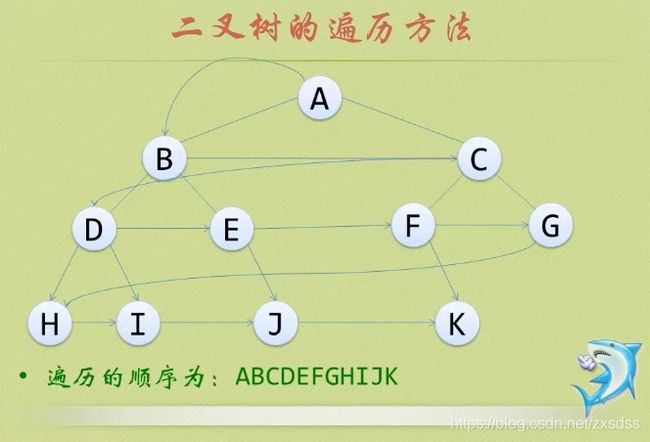
4.层次遍历

若树为空，则空操作返回。否则，从树的第一层，也就是根节点开始访问，从上到下逐层遍历，在同一层中，按从左到右的顺序结点逐个访问。

四.线索二叉树

概念

当我在查找某个结点的时候，想要知道这个节点的前驱结点或者后继结点，我该怎么做？

1.我是不是可以先序遍历或者后序遍历得到他们的前驱或者后继

2.我是不是可以开辟内存空间，对于每个结点增加一个指向它的前驱，增加一个指向它的后继

利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针，这些指针称为线索，加上线索的二叉树称为线索二叉树。

线索二叉树的遍历

void ThInOrder(TBTNode* tb)
{
     
	TBTNode* p = tb->lchild;
	while (p != tb) {
     
		while (p->ltag == 0) p = p->lchild;
		cout << p->data;
		while (p->rtag == 1 && p->rchild != tb) {
     
			p = p->rchild;
			cout << p->data;
		}
		p = p->rchild;
	}
}

五.哈夫曼树

一.概述

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。树的带权路径长度，用WPL表示

哈夫曼树的基本原理是让查找效率更高，让出现频率更高的元素（权重大的），拥有较少的查找次数。

二.应用

哈夫曼编码：规定哈夫曼树中的左分支为0、右分支为1，则从根结点到每个叶子结点所经过的分支对应的0和1组成的序列便是该结点对应字符的编码。

六.平衡二叉树

1.概念

若一颗二叉树中每个结点的左右子树的高度最多相差1，则称此二叉树为平衡二叉树。

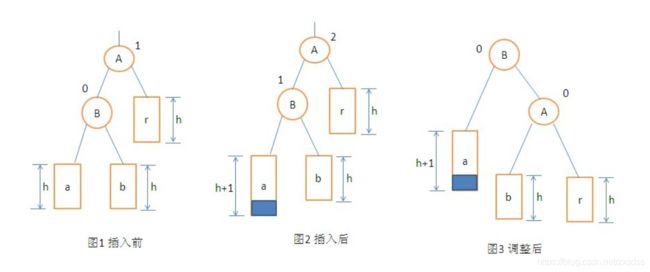
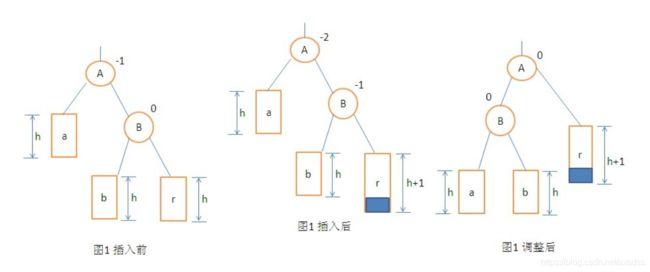
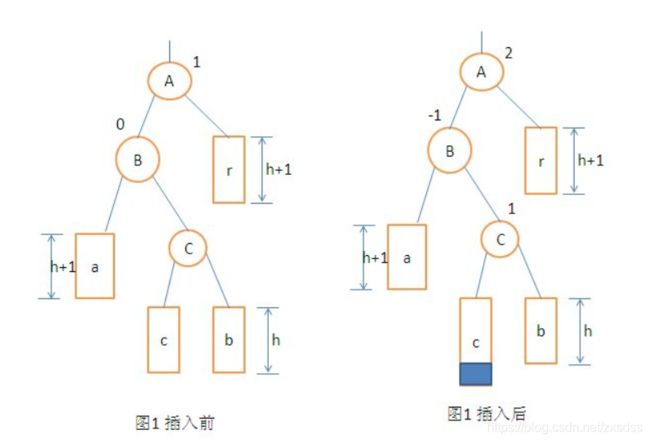
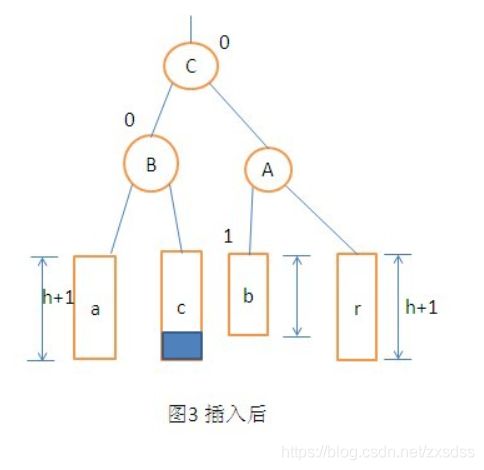
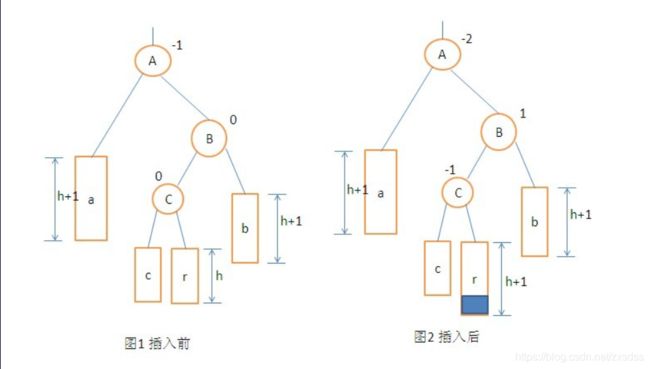
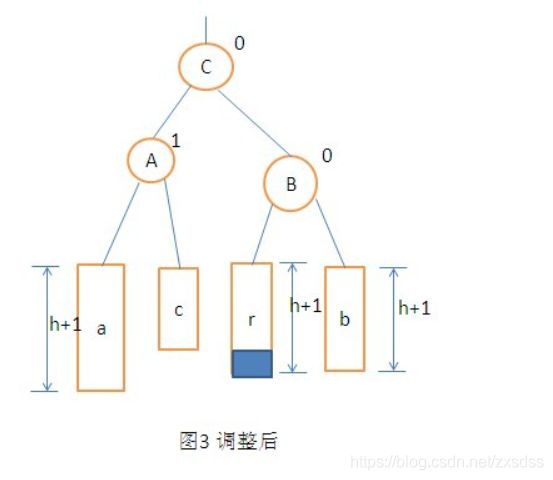
2.平衡二叉树插入结点

1.LL型调整

2.RR型调整

3.LR型调整

4.RL型调整

七.疑难问题及解决方案

1.7-3(map) QQ帐户的申请与登陆 (25 分)

#include
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
 
map<string,string>m;
 
int main()
{
     
	int n;
	char c;
	string s1,s2;
	cin>>n;
	while(n--)
	{
     
		cin>>c>>s1>>s2;
		if(c=='L')
		{
     
			if(m[s1].empty())
				cout<<"ERROR: Not Exist"<<endl;
			else
			{
     
				if(m[s1]!=s2)
					cout<<"ERROR: Wrong PW"<<endl;
				else
					cout<<"Login: OK"<<endl;
			}
		}
		else
		{
     
			if(m[s1].empty())
			{
     
				m[s1]=s2;
				cout<<"New: OK"<<endl;
			}
			else
				cout<<"ERROR: Exist"<<endl;
		}
	}
	return 0;
}

对于map的应用还不够熟练。