乔列斯基(Cholesky)法解方程(python,数值积分)
第四课 乔列斯基(Cholesky)法解方程
首先要清楚二次型和正定矩阵
“二次型”可以定义为n个变量的二次表达式

![]()
如果这个二次型的所有变量X的值都等于或大于零,那么这个二次型就是“正的”。如果x1 = x2 = = xn =0的值为零时的正型称为“正定的”。非正定的正二次型称为“半正定”。
使用我们通常的向量和矩阵表达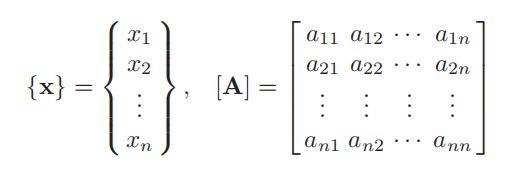
二次型可以简便地表达为
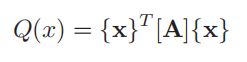
其中[A]是“二次型Q(x)的矩阵”。如果|A|为零或非零,Q(x)是“奇异的”或非奇异的。
如果二次型{x}T [A]{x}是正定的,行列式

必须是正的
举例
三个值全是正的

因此二次型形式为
因为只有当x1 = x2 = x3 = 0时,它才能为零,所以它是正定的。
乔列斯基法
当系数矩阵[A]对称正定时,通过让[U]为[L]的转置,可以得到一个不同的因式分解。这个因式分解是可以写成


可以很容易得出,L11的平方=A11,L11L21=A12,L31L11=A13,所以,下面这个例子为
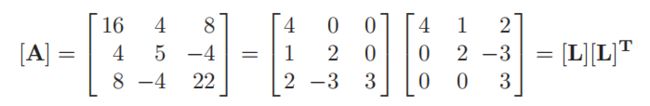
注意:如果对称矩阵不是正定的,那么乔列斯基法将不再适用,因为会分解出负值。
举例如下:
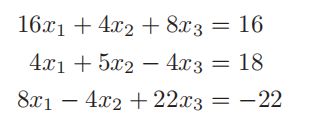
系数矩阵是正定对称的,则可以分解为
![]()

解出l值为

‘向前迭代法’

得到
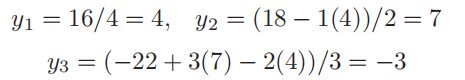
‘向后迭代法’

得到

带宽方程
在许多工程应用中,当系数具有“带状”结构时。这意味着非零系数聚集在从矩阵左上角到右下角的对角线周围。一个典型的例子如图所示,在任何一行的“主对角线”的两边都不超过两个非零系数。这个系统的“带宽”是5。如果系数是对称的,则只需要存储和操作主对角线和每行两个以上的系数。在这种情况下,“半带宽”被称为2(不包括主对角线)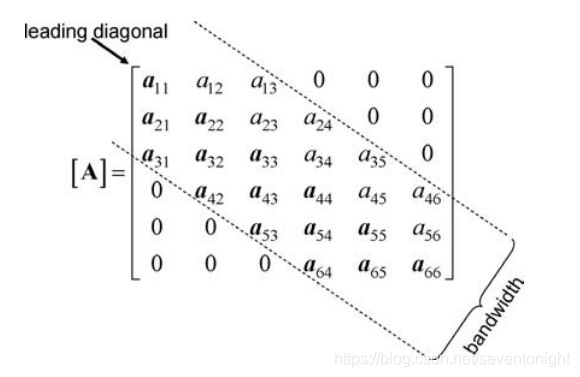
如果[A]是对称的,并且我们希望只在下面的三角形中存储非零项,如图2.1中的粗体所示,则只涉及15项,而不是36项(如果我们存储整个矩阵)。

这仍然有点低效,因为我们必须存储18个术语,包括前两行中不需要的零。然而,这种存储方法的优点是每行有三个项(半带宽加1),这使得编程相当容易。主对角线位于第三列。
代码如下:
分为一个主程序和两个子程序,子程序为带宽形式的下三角分解cholin,和乔列斯基下的下三角向后迭代法chobac。
#使用带宽储存的乔列斯基LLT分解
import numpy as np
import math
import B
n=3
iw=2
iwp1=iw+1
lb=np.array([[0,0,16],[0,4,5],[8,-4,22]],dtype=np.float)
b=np.array([[4],[2],[5]],dtype=np.float)
print('带宽系数')
for i in range(1,n+1):
print(lb[i-1,:])
print('右手边向量',b)
B.cholin(lb)
print('带宽形式下三角')
for i in range(1,n+1):
print(lb[i-1,:])
B.chobac(lb,b)
print('解向量',b) cholin
def cholin(kb):
n=kb.shape[0]
iw=kb.shape[1]-1
for i in range(1,n+1):
x=0
for j in range(1,iw+1):
x=x+kb[i-1,j-1]**2
kb[i-1,iw]=(kb[i-1,iw]-x)**0.5
for k in range(1,iw+1):
x=0
if i+k<=n:
if k!=iw:
for l in range(iw-k,0,-1):
x=x+kb[i+k-1,l-1]*kb[i-1,l+k-1]
ia=i+k
ib=iw-k+1
kb[ia-1,ib-1]=(kb[ia-1,ib-1]-x)/kb[i-1,iw]chobac
def chobac(kb,loads):
n=kb.shape[0]
iw=kb.shape[1]-1
loads[0,0]=loads[0,0]/kb[0,iw]
for i in range(2,n+1):
x=0
k=1
if i<=iw+1:
k=iw-i+2
for j in range(k,iw+1):
x=x+kb[i-1,j-1]*loads[i+j-iw-2,0]
loads[i-1,0]=(loads[i-1,0]-x)/kb[i-1,iw]
loads[n-1,0]=loads[n-1,0]/kb[n-1,iw]
for i in range(n-1,0,-1):
x=0
l=i+iw
if i>n-iw:
l=n
m=i+1
for j in range(m,l+1):
x=x+kb[j-1,iw+i-j]*loads[j-1,0]
loads[i-1,0]=(loads[i-1,0]-x)/kb[i-1,iw]
终端输出结果:

程序结果与计算结果一致
下面附带一个面向对象的cholesky分解
import numpy as np
import math
class LinerSolver:
def __init__(self, A, b):
self.A = A
self.b = b
def CholeskiSolver(self):
n = len(self.A)
# 分解 [A] = [L] [L^T]
for k in range(n):
self.A[k,k] = math.sqrt(self.A[k,k] - np.dot(self.A[k,0:k], self.A[k,0:k]))
for i in range(k+1,n):
self.A[i,k] = (self.A[i,k] - np.dot(self.A[i,0:k], self.A[k,0:k])) / self.A[k,k]
for k in range(1,n):
self.A[0:k,k] = 0.0
# 求解 [L]{y} = {b}
for k in range(n):
self.b[k] = (self.b[k] - np.dot(self.A[k,0:k], self.b[0:k])) / self.A[k,k]
# 求解 [L^T]{x} = {y}
for k in range(n-1,-1,-1):
self.b[k] = (self.b[k] - np.dot(self.A[k+1:n,k], self.b[k+1:n])) / self.A[k,k]
return self.b
A = np.array([ [ 4, -1, 1],
[-1, 4.25, 2.75],
[1, 2.75, 3.5] ])
b = np.array([4, 6, 7.25])
cls = LinerSolver(A, b) #创建一个求解器的实例cls
x = cls.CholeskiSolver() #调用Choleski法求解
print(x)