移位取逆迭代(shifted inverse iteration)求最近特征值和特征向量(python,数值积分)

第二十七篇 移位取逆迭代求最近特征值和特征向量

移位逆迭代

一种比“最大”特征值法更直接实现向量迭代收敛的的特征值方法是将移位向量迭代法改写为下面形式

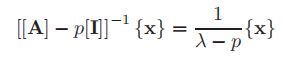
其中p是一个标量“移位”值，[I]是单位矩阵，λ是[a]的特征值。如特征值编程基础所示，[[A]−p [I]−1的特征向量与[A]的特征向量相同，但可以证明[[A]−p [I]−1的特征值是1/(λ−p)。因此，[[A]−p[I]]−1的最大特征值导致[A]的特征值最接近p。因此，如果[[A]−p[I]]−1的最大特征值是μ，则[A]最接近p的特征值为

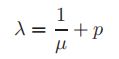
对于小型的矩阵，只需要求[[A]−p[I]]的逆，并使用逆迭代求解方程，与线性方程求解中使用的算法完全相同。然而，对于较大的矩阵，线性方程中因式分解法是更加适用的，特别是当处理多个右侧向量值和一个常系数矩阵时。因此，在正常的移位迭代法中，必须在每次迭代中计算

而在逆迭代中需要计算

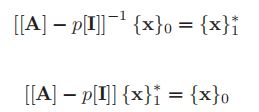
通过使用子程序lufac，因式分解[A]−p[I]得到

得

如果现在让

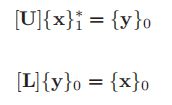
把求解过程分为两步，先求解{y}0，再求解{x}1。这种方法和之前介绍过的从前和后迭代得方式完全一样，所以要使用之前得子程序,subfor和subbac，详情请看LDLT分解高斯消元
通过在系统中替换p得方式，全部得特征值都能求出。
计算实例
使用移位求逆方法发现下面矩阵最接近2得特征值

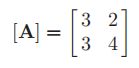
对这种小型问题，可以直接通过手算求出，让

当在这个例子中p取2时

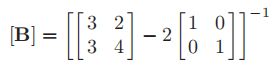
因此

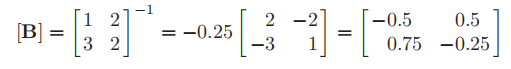
让{x}0 = {1 1}t 和{x}∗k是{x}k正交化前的值。
第一迭代(k=1)

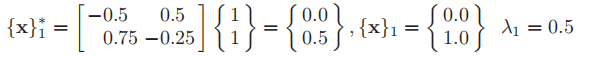
第二次迭代(k=2)

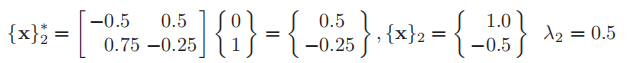
第三次迭代(k=3)


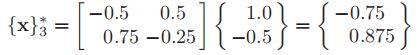
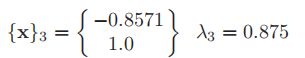
第四次迭代(k=4)

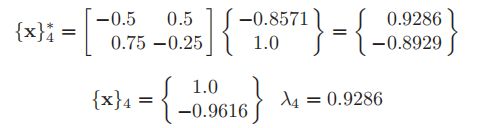
许多次迭代之后

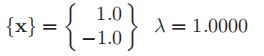
程序如下：
其中有一个主程序和四个子程序，分别为检查收敛的子程序checkit，因式分解的子程序lufac，从前迭代法子程序subfor，从后迭代法子程序subbac。

#特征值和特征向量的移位求逆向量迭代
import numpy as np
import B
n=3;tol=1.0e-5;limit=100;shift=20.0
lower=np.zeros((n,n))
upper=np.zeros((n,n))
a=np.array([[10,5,6],[5,20,4],[6,4,30]],dtype=np.float)
x1=np.zeros((n,1))
x=np.ones((3,1),dtype=np.float)
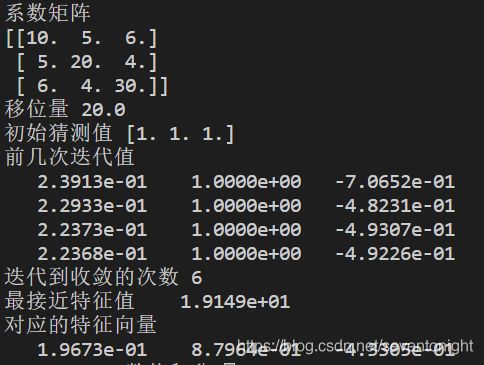
print('系数矩阵')
print(a[:])
print('移位量',shift)
print('初始猜测值',x[:,0])
for i in range(1,n+1):
    a[i-1,i-1]=a[i-1,i-1]-shift
B.lufac(a,lower,upper)
print('前几次迭代值')
x1[:,0]=x[:,0]
iters=0
while(True):
    iters=iters+1
    B.subfor(lower,x1)
    B.subbac(upper,x1)
    big=0.0
    for i in range(1,n+1):
        if abs(x1[i-1,0])>abs(big):
            big=x1[i-1,0]
    x1[:,0]=x1[:,0]/big
    if  B.checkit(x1,x,tol)==True or iters==limit:
        break
    x[:,0]=x1[:,0]
    if iters<5:
        for i in range(1,n+1):
            print("{:13.4e}".format(x[i-1,0]),end=" ")
        print(end="\n")
l2=np.linalg.norm(x1)
x1[:,0]=x1[:,0]/l2
print('迭代到收敛的次数',iters)
print('最接近特征值',"{:13.4e}".format(1.0/big+shift))
print('对应的特征向量')
for i in range(1,n+1):
    print("{:13.4e}".format(x1[i-1,0]),end=" ")

checkit	

def checkit(loads,oldlds,tol):
#检查多个未知数的收敛
  neq=loads.shape[0]
  big=0.0
  converged=True
  for i in range(1,neq+1):
    if abs(loads[i-1,0])>big:
      big=abs(loads[i-1,0])
  for i in range(1,neq+1):
    if abs(loads[i-1,0]-oldlds[i-1,0])/big>tol:
      converged=False
  checkit=converged
  return  checkit

lufac

ef lufac(a,lower,upper):
  n=a.shape[0]
  upper[0,:]=a[0,:]
  for i in range(1,n+1):
    lower[i-1,i-1]=1.0
  for k in range(1,n):
    if abs(upper[k-1,k-1])>1.0e-10:
      for i in range(k+1,n+1):
#下三角分解
        for j in range(1,i):
          total=0
          for l in range(1,j):
            total=total-lower[i-1,l-1]*upper[l-1,j-1]
          lower[i-1,j-1]=(a[i-1,j-1]+total)/upper[j-1,j-1]
#上三角分解
        for j in range(1,n+1):
          total=0
          for l in range(1,i):
            total=total-lower[i-1,l-1]*upper[l-1,j-1]
          upper[i-1,j-1]=a[i-1,j-1]+total
    else:
      print('有0向量在第',k,'行')
      break

subfor

def subfor(a,b):
#一个下三角的从前迭代法
  n=a.shape[0]
  for i in range(1,n+1):
    total=b[i-1]
    if i>1:
      for j in range(1,i):
        total=total-a[i-1,j-1]*b[j-1]
    b[i-1]=total/a[i-1,i-1]

subbac

def subbac(a,b):
#一个下三角的从后迭代法
  n=a.shape[0]
  for i in range(n,0,-1):
    total=b[i-1]
    if i<n:
      for j in range(i+1,n+1):
        total=total-a[i-1,j-1]*b[j-1]
    b[i-1]=total/a[i-1,i-1]

终端输出结果