Leetcode——贪心算法(c++和java实现)
本来有一段时间没有刷题了,但是突然发现了这本书LeetCode 101 - A LeetCode Grinding Guide (C++ Version),感觉真不错,思路简单清晰,没有过多的废话。乘机学习分享一下:
链接:https://pan.baidu.com/s/14jsfK97IiorZImmQXsmS4g
提取码:lhwv
本书代码都是c++写的,本文会用c++和java复现一遍并且整理课后例题。
照着里面的顺序刷,第一章就是贪心算法的啦,花了两天空闲的时间刷完,总结一下。
1.分配问题
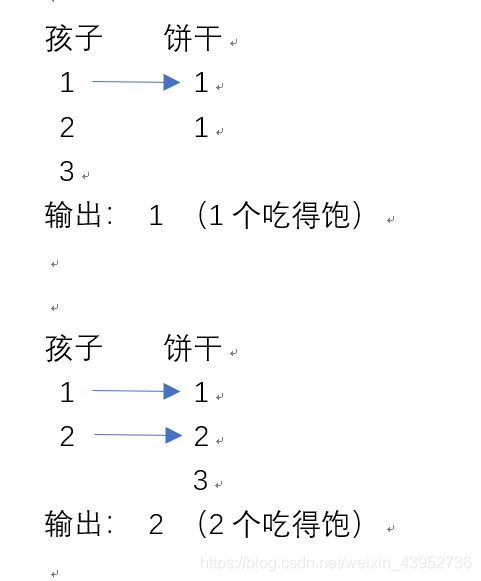
455.分发饼干
题目描述: 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
输入: g = [1,2,3], s = [1,1]
输出: 1
题解:
这道题是比较典型的贪心算法例题,因为饥饿度最小的孩子最容易吃饱,所以我们先考虑这个孩子。为了尽量使得剩下的饼干可 以满足饥饿度更大的孩子,所以我们应该把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。
//c++
//使用sort时要导入#include //java
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int child = 0, cookie = 0;
while (child < g.length && cookie < s.length) {
if (g[child] <= s[cookie])
++child;
++cookie;
}
return child;
}
}
135.分发糖果
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
题解:
这一 道题也是运用贪心策略,但我们只需要简单的两次遍历即可:
①把所有孩子的糖果数初始化为 1;
②先从左往右遍历一遍,如果右边孩子的评分比左边的高,则右边孩子的糖果数更新为左边孩子的糖果数加1;
③再从右往左遍历一遍,如果左边孩子的评分比右边的高,且左边孩子当前的糖果数不大于右边孩子的糖果数,则左边孩子的糖果数更新为右边孩子的糖果数加1。通过这两次遍历,分配的糖果就可以满足题目要求了。
//c++
int candy(vector<int>& ratings) {
int size = ratings.size();
if(size < 2)
return size;
vector<int> num(size,1);//定义size个值为1的vector;
for(int i = 1; i < size; i++){
if(ratings[i] > ratings[i - 1])
num[i] = num[i - 1] + 1;
}
for(int i = size - 1; i > 0; i--){
if(ratings[i - 1] > ratings[i])
num[i - 1] = max(num[i - 1], num[i] + 1);
}
//accumulate定义在#include中,第三个形参则是累加的初值。
return accumulate(num.begin(), num.end(), 0);
}
//java
public int candy(int[] ratings) {
int size = ratings.length;
if(size < 2)
return size;
int[] num = new int[size];
Arrays.fill(num,1);//java中可以用Arrays.fill(),把数组中的值都初始化为某个数。
for(int i = 1; i < size; i++){
if(ratings[i] > ratings[i - 1])
num[i] = num[i - 1] + 1;
}
for(int i = size - 1; i > 0; i--){
if(ratings[i - 1] > ratings[i])
num[i - 1] = Math.max(num[i - 1], num[i] + 1);
}
int sum = 0;
for(int l : num){
sum += l;
}
return sum;
}
2.区间问题
435.无重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
- 可以认为区间的终点总是大于它的起点。
- 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例1
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例2
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
题解:
①在选择要保留区间时,区间的结尾十分重要:选择的区间结尾越小,余留给其它区间的空间 就越大,就越能保留更多的区间。因此,我们采取的贪心策略为,优先保留结尾小且不相交的区 间。
②我们这里使用 C++ 的 Lambda,结合 std::sort() 函数进行自定义排序。(下文有详细说明sort用法)在样例中,排序后的数组为 [[1,2], [1,3], [2,4]]。按照我们的贪心策略,首先初始化为区间 [1,2];由于 [1,3] 与 [1,2] 相交,我们跳过该区间;由于 [2,4] 与 [1,2] 不相交,我们将其保留。因 此最终保留的区间为[[1,2],[2,4]]。
//c++
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.size() <= 1)
return 0;
sort(intervals.begin(), intervals.end(),[](vector<int> a, vector<int> b){
return a[1] < b[1];
});//区间尾升序排列;
int n = intervals.size();
int result = 0;
int pre = intervals[0][1];
for(int i = 1; i < n; i++){
if(pre > intervals[i][0])
result++;
else
pre = intervals[i][1];
}
return result;
}
//java
public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length <= 1) return 0;
// 按 end 升序排序
Arrays.sort(intervals, new Comparator<int[]>(){
public int compare(int[] a, int[] b){
return a[1]-b[1];
}
});
// 至少有一个区间不相交
int count = 0;
int n = intervals.length;
// 排序后,第一个区间就是 x
int pre = intervals[0][1];
for(int i = 1; i < n; i++){
if(pre > intervals[i][0])
count++;
else
pre = intervals[i][1];
}
return count;
}
这里关于c++的sort自定义的写法,采用lammda表达式。
sort自定义一般用法是:
sort(nums.begin(), nums.end(), cmp);
bool cmp(const int& a, const int& b)
{
return a > b; //从大到小排序
}
也可以用lammda表达式
vector res;
sort(ins.begin(), ins.end(), [](Interval a, Interval b){return a.start < b.start;});
在Java中,使用Arrays.sort方法,使用匿名内部类,实现Comparator接口,重写compare方法即可。
也可以更改为lambda表达式
import java.util.*;
public class Main {
public static void main(String[] args){
Integer[] arr = {
5,4,7,9,2,12,54,21,1};
//降序
Arrays.sort(arr, new Comparator<Integer>() {
public int compare(Integer a, Integer b) {
return b-a;
}
});
System.out.println(Arrays.toString(arr));
}
}
练习:
605.种花问题
假设你有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花卉不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给定一个花坛(表示为一个数组包含0和1,其中0表示没种植花,1表示种植了花),和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花?能则返回True,不能则返回False。
示例 1:
输入: flowerbed = [1,0,0,0,1], n = 1
输出: True
示例 2:
输入: flowerbed = [1,0,0,0,1], n = 2
输出: False
题解:
①当该位置为值为0的,则有种花的可能,接着判断前一个和后一个是否也为0,如果符合,则种花的数量+1。
②这里需要考虑第0个位置的情况,如果第1个位置也为0,则第一个位置可种花。最后一个位置也是同样的道理,当最后一个位置为0,则考虑倒数第二个位置是否为0即可。
③最后将种花的数量和n比较大小即可。
//c++
//java代码基本一样就不写了
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int i = 0;
int count = 0;
while(i < flowerbed.size()){
if(flowerbed[i] == 0 && (i == 0 || flowerbed[i - 1] == 0) && (i == flowerbed.size() - 1 || flowerbed[i + 1] == 0)){
flowerbed[i] = 1;
count++;
}
if(count >= n)
return true;
i++;
}
return false;
}
452.用最少数量的箭引爆气球
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]]
输出:2
示例 4:
输入:points = [[1,2]]
输出:1
示例 5:
输入:points = [[2,3],[2,3]]
输出:1
题解:
这道题的做法和(上文)无重叠区间的做法基本是一样的,先初始化箭数等于区间数,然后区间有重叠(当前区间的末尾 >= 另一个区间的起始位置)则箭数减一。
//c++
int findMinArrowShots(vector<vector<int>>& points) {
if(points.size() == 0)
return 0;
int shotNum = points.size();
sort(points.begin(), points.end(), [](vector<int> a, vector<int> b){
return a[1] < b[1];
});
int end = points[0][1];
for(int i = 1; i < points.size(); i++){
if(points[i][0] <= end){
shotNum--;
}else{
end = points[i][1];
}
}
return shotNum;
}
763.划分字母区间
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
输入:S = “ababcbacadefegdehijhklij”
输出:[9,7,8]
解释:
划分结果为 “ababcbaca”, “defegde”, “hijhklij”。
每个字母最多出现在一个片段中。
像 “ababcbacadefegde”, “hijhklij” 的划分是错误的,因为划分的片段数较少。
题解:
这道题的想法比较简单,先用map记录下每个字母出现的最后位置,然后i遍历一遍字符串,当出现一个新字母时,end更新为当前存储位置较远的数,当end等于遍历的数i时候,说明前面的字符串可以单独分离开(区间内的字母在别的地方没有出现了)。
//c++
vector<int> partitionLabels(string S) {
vector<int> result;
unordered_map<char, int> map;
for(int i = 0; i < S.length(); i++){
map[S[i]] = i;//记录各个字符和它的最后出现的位置。
}
int start = 0, end = 0;
for(int i = 0; i < S.length(); i++){
end = max(end, map[S[i]]);
if(i == end){
result.push_back(end - start + 1);
start = i + 1;
}
}
return result;
}
//java
public static List<Integer> partitionLabels(String s){
List<Integer> result = new ArrayList<>();
Map<Character,Integer> map = new HashMap<>();
for(int i = 0; i < s.length(); i++){
map.put(s.charAt(i),i);
}
int start = 0;
int end = 0;
for(int i = 0; i < s.length(); i++){
end = Math.max(end, map.get(s.charAt(i)));
if(i == end){
result.add(end - start + 1);
start = i + 1;
}
}
return result;
}
122. 买股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
题解:
这道题有个很简单的做法就是,只要遍历一遍,后一个比前一个大,则有收益,它们之间的差即为收益的大小,然后进行累加即可。
int maxProfit(vector<int>& prices) {
int sum = 0;
for(int i = 1; i < prices.size(); i++){
//这里也可改为if判断prices后一个是否比前一个大,大则更新。
sum += max(0,prices[i] - prices[i - 1]);
}
return sum;
}
406.根据身高重建队列
假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对 (h, k) 表示,其中 h 是这个人的身高,k 是应该排在这个人前面且身高大于或等于 h 的人数。 例如:[5,2] 表示前面应该有 2 个身高大于等于 5 的人,而 [5,0] 表示前面不应该存在身高大于等于 5 的人。
编写一个算法,根据每个人的身高 h 重建这个队列,使之满足每个整数对 (h, k) 中对人数 k 的要求。
示例:
输入:[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
输出:[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
题解:
本题需要用到排序+插入。先对人群进行排序,从高到低排序,同高则按照k小的排在前面,这个能够最大程度的满足题意。
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
排序后变成
[[7,0],[7,1],[6,1],[5,0],[5,2],[4,4]]
然后遍历逐个按照k的值插入,这样身高较高的先插入队列中,插入第k个位置,也满足前面有k个人。后面身高低的插入前面也不影响身高高的前面只有k个人。
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), [](vector<int> a,vector<int> b){
return a[0] > b[0] || (a[0] == b[0] && a[1] < b[1]);
});
vector<vector<int>> ans;
int j = 1;
for (const vector<int>& person: people) {
ans.insert(ans.begin() + person[1], person);//在迭代器中下标为person[1]的元素前插入新元素person;
//因为它排后面的都是较小的身高,所以插入到前面多少个都无所谓。不会影响前面的对应身高 前面的人的个数。
}
return ans;
}
//java
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people, new Comparator<int[]>() {
public int compare(int[] person1, int[] person2) {
if (person1[0] != person2[0]) {
return person2[0] - person1[0];
} else {
return person1[1] - person2[1];
}
}
});
List<int[]> ans = new ArrayList<int[]>();
for (int[] person : people) {
ans.add(person[1], person);
}
return ans.toArray(new int[ans.size()][]);//List 转 Int[][];
}
665.非递减数列
给你一个长度为 n 的整数数组,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。
我们是这样定义一个非递减数列的: 对于数组中所有的 i (0 <= i <= n-2),总满足 nums[i] <= nums[i + 1]。
示例 1:
输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个4变成1来使得它成为一个非递减数列。
示例 2:
输入: nums = [4,2,1]
输出: false
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。
题解:
它这个测试数据不够满足所有情况,由题知,我们要考虑的情况是当前数nums[i] > nums[i+1]的情况,但是随后更新nums[i],还是更新nums[i]确是不确定的,本题主要有三种情况:
例1 输入的是 4 2 3 4 > 2, 4前面没有值,可将4更新为2,即为 2,2,4
例2 输入的是 -1 4 2 3 4 > 2,4前面的值-1小于2,4可更新为2,即为-1,2,2,3
例3 输入 2 3 3 2 4 3 > 2,3前面的值3大于2,2可更新为3,即为2,3,3,3,4
主要是读多一位进行判断。
bool checkPossibility(vector<int>& nums) {
if(nums.size() <= 1)
return true;
int count = 0;
for(int i = 1; i < nums.size() && count < 2; i++){
if(nums[i - 1] <= nums[i])
continue;
count++;
if(i - 2 >= 0 && nums[i - 2] > nums[i]){
nums[i] = nums[i - 1];
}else{
nums[i - 1] = nums[i];
}
}
return count <= 1;
}
dddd