大数据预处理:缺失值处理、数据标准化、0-1缩放、归一化、二值化、独热编码和标签编码
数据预处理:数据标准化、0-1缩放、归一化、独热编码和标签编码、缺失值处理
- 前言
- 一、缺失值处理
-
- 1.1 处理方式
- 1.2 简单示例
- 1.3 缺失值处理步骤
- 1.4 实例展示
- 二、数据标准化
-
- 2.1 标准化的定义
- 2.2 为什么要进行数据标准化?
- 2.3 实际操作
- 三、0-1缩放
-
- 3.1 数据缩放化定义
- 3.2 实际操作
- 四、归一化
-
- 4.1 数据归一化定义
- 4.2 实例操作
- 五、二值化
-
- 5.1 二值化定义
- 5.2 实际操作
- 六、独热编码
-
- 6.1 独热编码定义
- 6.2 实例操作
- 七、标签编码
-
- 7.1 标签编码定义
- 7.2 实例操作
- 总结
手动反爬虫: 原博地址
知识梳理不易,请尊重劳动成果,文章仅发布在CSDN网站上,在其他网站看到该博文均属于未经作者授权的恶意爬取信息
如若转载,请标明出处,谢谢!
前言
在进行数据分析之前,需要了解数据的情况,有时候拿到的数据并不是想象中的完美数据,那么就需要进行预处理,才能使用。为了系统的缕清预处理的一般的步骤,这里进行详细的梳理,采用sklearn工具包和手写代码验证的方式进行。
一、缺失值处理
1.1 处理方式
最常见的数据情况就是缺失部分数据,那么怎么处理缺失值?有没有固定的公式呢?处理方式如下:
-
删除:缺失样本量 非常大,删除整个字段;如果缺失量较少,且 难以填充 则删除缺失样本
-
填充:缺失量 小于10%,根据缺失变量的数据分布采取 均值(正态分布) 或 中位数(偏态分布) 进行填充
-
模拟或预测缺失样本:根据样本的数据分布,生成 随机值填充(插值);使用与缺失相比相关性非常高的特征,建立模型,预测缺失值
这里先介绍“删除”和“填充”的方式,最后的随机值填充也几乎类似,使用random随机数的功能即可
1.2 简单示例
先进行简单示例:进行单字段缺失值的处理,采用均值填充
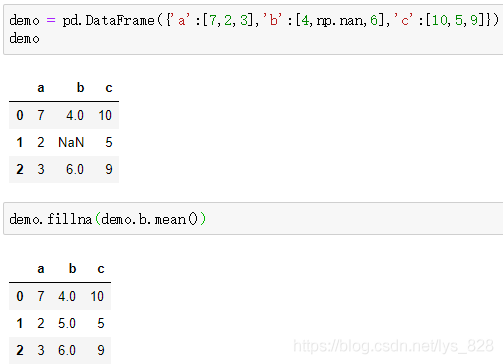
demo = pd.DataFrame({
'a':[7,2,3],'b':[4,np.nan,6],'c':[10,5,9]})
demo
demo.fillna(demo.b.mean())
输出的结果为:(由于要计算出每个字段的均值,而不是采用固定的值进行填充,所以采用此方法填充单个字段没问题,多个字段就必须一行一行代码的执行了)
比如,这里进行多行缺失值的处理
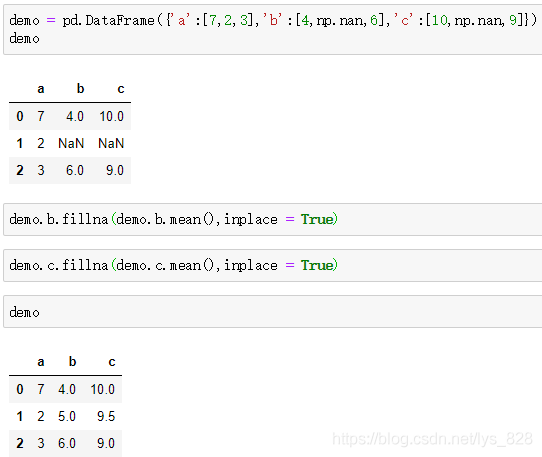
demo = pd.DataFrame({
'a':[7,2,3],'b':[4,np.nan,6],'c':[10,np.nan,9]})
demo.b.fillna(demo.b.mean(),inplace = True)
demo.c.fillna(demo.c.mean(),inplace=True)
demo
输出的结果为:(如果字段多的话,可以发现规律,直接遍历循环就可以了)
那有没有直接可以调用的函数进行各字段均值的填充?当然是有的,下面就是使用sklearn工具包进行演示
1.3 缺失值处理步骤
采用sklearn模块中的SimpleImputer函数进行处理,使用的步骤共四步
- (1)从模块中导入函数
- (2)设定填充的对象和填充的方式
- (3)选取数据
- (4)处理数据
from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer(missing_values = np.nan, strategy = 'mean')
X = [[7,4,10],[2,np.nan,np.nan],[3,6,9]]
imp_mean.fit(X)
imp_mean.transform(X)
输出的结果为:(这里是直接进行举例的数据,随机设定的,接下来就是进行实例操作演示)
array([[ 7. , 4. , 10. ],
[ 2. , 5. , 9.5],
[ 3. , 6. , 9. ]])
1.4 实例展示
实例操作,这里使用消费记录的数据进行展示
#首先准备数据,这里是截取csv文件汇总的部分数据
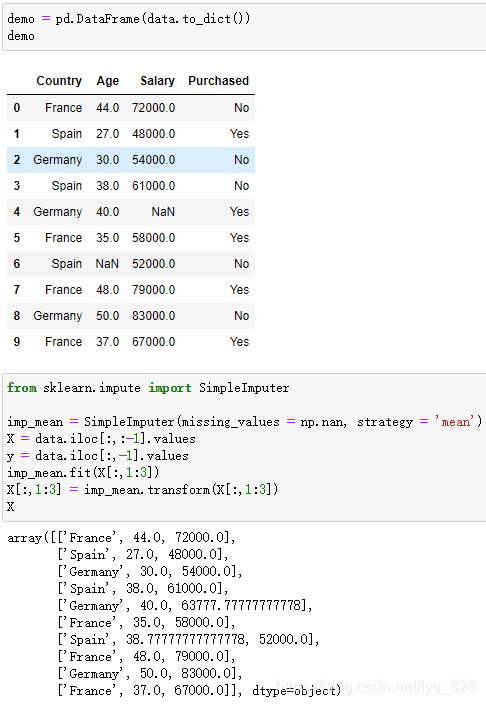
demo = {
'Country': {
0: 'France',1: 'Spain',2: 'Germany',3: 'Spain',4: 'Germany',5: 'France',6: 'Spain',7: 'France',8: 'Germany',9: 'France'},
'Age': {
0: 44.0,1: 27.0,2: 30.0,3: 38.0,4: 40.0,5: 35.0,6: nan,7: 48.0,8: 50.0,9: 37.0},
'Salary': {
0: 72000.0,1: 48000.0,2: 54000.0,3: 61000.0,4: nan,5: 58000.0,6: 52000.0,7: 79000.0,8: 83000.0,9: 67000.0},
'Purchased': {
0: 'No',1: 'Yes',2: 'No',3: 'No',4: 'Yes',5: 'Yes',6: 'No',7: 'Yes',8: 'No',9: 'Yes'}}
#第一步:从模块中导入函数
from sklearn.impute import SimpleImputer
#第二步:填充的对象和填充的方式
imp_mean = SimpleImputer(missing_values = np.nan, strategy = 'mean')
#第三步:选取数据
X = data.iloc[:,:-1].values
y = data.iloc[:,-1].values #这里是标签的信息,本篇博客暂时用不到
imp_mean.fit(X[:,1:3])
#第四步:处理数据
X[:,1:3] = imp_mean.transform(X[:,1:3])
X
输出结果为:(Age和Salary两个字段的缺失数据就处理完毕了,也可以尝试选择不同的处理对象和处理方式)
二、数据标准化
2.1 标准化的定义
标准化的定义:又被称为均值移除(mean removal),对不同样本的同一特征值进行处理,最终均值为0,标准差为1,采用此种方式我们只需要使用如下公式即可。
x s c a l e d = x − m e a n s d ⇒ z = X − μ σ x_{scaled} = \frac{x-mean}{sd} \Rightarrow z = \frac{X-\mu}{\sigma} xscaled=sdx−mean⇒z=σX−μ
- m e a n : mean: mean:数据均值
- s d : sd: sd:数据标准差
2.2 为什么要进行数据标准化?
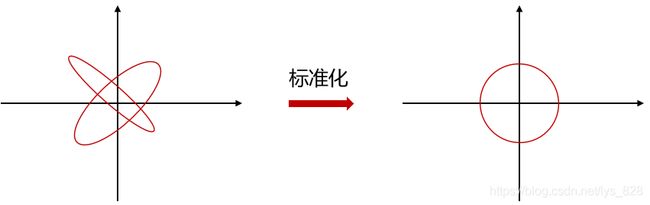
在机器学习中,很多的算法和评估模型的好坏的方法都是基于距离(残差)的处理,也就是 ( x i − x ) 2 (x_{i} -x)^2 (xi−x)2或者是 ( y i − y ) 2 (y_{i} -y)^2 (yi−y)2,因此在进行数据随机采样的时候应该避免不同距离对模型影响,故需要进行标准化处理,保准随机取的数据是等距离的。说人话,借用图像举例,就是要把不同的椭圆,最后处理成为正圆,这样在圆上取任意值到原点的距离都相等。
2.3 实际操作
import numpy as np
from sklearn import preprocessing
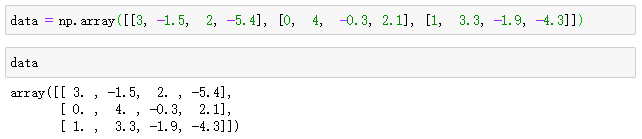
data = np.array([[3, -1.5, 2, -5.4], [0, 4, -0.3, 2.1], [1, 3.3, -1.9, -4.3]])
data
输出结果为:(数据随机设定的,方便后面进行手动验证)
按照标准化的公式,要先计算均值和方差,那么有个问题就来了:计算的数据是横向(一行数据,axis = 1),还是纵向(一列数据,axis = 0)的呢?对照前面缺失值处理的实例操作的部分,可以知道每一列(纵向)都代表着一个字段的数据,而每一行却包含了所有字段中的一个数据,而在计算均值和方差时候应该选取的是某个字段进行,也就是需要计算纵向的数据
print('Mean: ',data.mean(axis = 0))
print('Standard Deviation: ', data.std(axis = 0))
import math
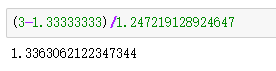
math.sqrt(((3-1.33333333)**2+(0-1.33333333)**2+(1-1.33333333)**2)/3)
输出结果为:1.247219128924647(这里只进行第一列的标准差的验证,其余列也是一样的,均值可以口算)
最终标准化后的结果为:(以第一列第一行的数据进行展示)
以上的过程虽然原理很简单,操作起来也不是很难,但是要是每次进行数据处理之前都得一个数据一个数据的挨个处理,就显着很浪费时间,也因此就可以使用preprocessing函数进行处理
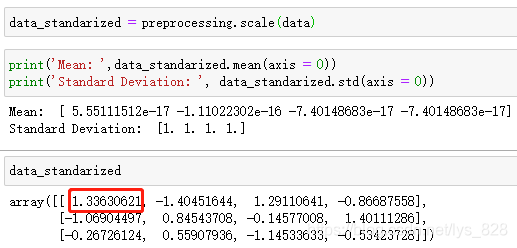
data_standarized = preprocessing.scale(data)
print('Mean: ',data_standarized.mean(axis = 0))
print('Standard Deviation: ', data_standarized.std(axis = 0))
data_standarized
输出的结果为:(python计算精度的问题,Mean这里实际上是为0的,10的负17次方,相当于很微小的数值了)
三、0-1缩放
3.1 数据缩放化定义
对不同样本的同一特征值,减去其最小值,除以(最大值-最小值), 最终原最大值为1,原最小值为0,这样在数据分析时可以有效的消除不同单位大小对最终结构的权重影响。(例如股票类信息,如果股价是5-7元之间浮动,但是每天成交量在100万上下,在不在采用缩放的模式下,成交量的数据权重会比股价高上几万倍,导致最终预测数据出现畸形)
x s c a l e d = x − x m i n x m a x − x m i n x_{scaled}=\frac{x-x_{min}}{x_{max}-x_{min}} xscaled=xmax−xminx−xmin
3.2 实际操作
在preprocessing函数中,使用MinMaxScaler方法
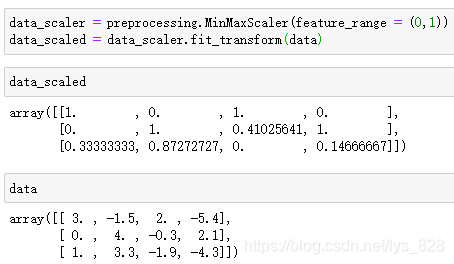
data_scaler = preprocessing.MinMaxScaler(feature_range = (0,1))
data_scaled = data_scaler.fit_transform(data)
data_scaled
输出结果为:(MinMaxScaler括号里可以进行参数的调整,根据自己的需求进行设置)
四、归一化
4.1 数据归一化定义
如果要调整特征向量中的值时,可以使用数据归一化,以便可以使用通用比例尺对其进行测量。机器学习中最常用的规范化形式之一是调整特征向量的值,使其总和为1(方便查找重要特征)。常见的处理方式有如下几种:L1模式, L2模式。
L1模式:理解就是加了绝对值的,也是常见的一种模式,还有其他很多的名字称呼,比如熟悉的曼哈顿距离,最小最对误差等。使用L1模式可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference)
L 1 : z = ∣ ∣ x ∣ ∣ 1 = ∑ i n ∣ x i ∣ L1: \space \space \space \space z = ||x||_{1} = \sum_{i}^{n}|x_{i}| L1: z=∣∣x∣∣1=i∑n∣xi∣
L2模式:理解就是加了平方的,是最常见最常用的一种模式,也有其他的称呼,比如使用最多的欧氏距离就是L2模式。通常用来做优化目标函数的正则化项,放置模型为了迎合训练集而过于复杂造成的过拟合情况,从而提高模型的泛化能力(可以参考一下逻辑回归进行信用卡欺诈预测案例中,如果惩罚项参数选择L2,结果会如何)
L 2 : z = ∣ ∣ x ∣ ∣ 2 = ∑ i n x i 2 L2: \space \space \space \space z =||x||_{2} = \sqrt{\sum_{i}^{n}x_{i}^{2}} L2: z=∣∣x∣∣2=i∑nxi2
4.2 实例操作
L1 模式
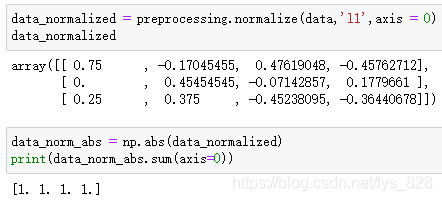
data_normalized = preprocessing.normalize(data,'l1',axis = 0)
data_normalized
data_norm_abs = np.abs(data_normalized)
print(data_norm_abs.sum(axis=0))
输出的结果为:(可以看出每一列转化后的数据相加都为1)
L2模式
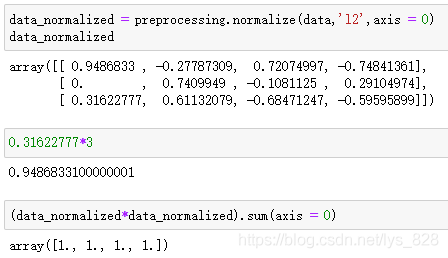
data_normalized = preprocessing.normalize(data,'l2',axis = 0)
data_normalized
#0.31622777*3
(data_normalized*data_normalized).sum(axis = 0)
输出的结果为:(每一列转化后的数据按照公式计算也都为1,比例保持不变)
五、二值化
5.1 二值化定义
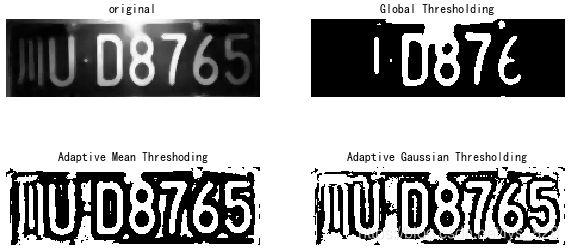
当我们要将数字特征向量转换为布尔向量时,可以使用二值化(就是根据自己指定的阈值,如果超过这个阈值就为1,小于这个阈值就为0)。在数字图像处理领域,图像二值化是将彩色或灰度图像转换为二进制图像(即仅具有两种颜色(通常是黑白)的图像)的过程。
此技术用于识别对象,形状,尤其是字符。通过二值化,可以将感兴趣的对象与发现对象的背景区分开,比如常见的车牌识别。
5.2 实际操作
data_binarized = preprocessing.Binarizer(threshold = 1.4).transform(data)
data
data_binarized
输出的结果为:(可以对比阈值,发现大于该值的数据都为1,小于的都为0,最后的数据有0和1)

六、独热编码
6.1 独热编码定义
对于经常需要处理各种 分散数值 的情况。实战当中我们并不需要存储这些值。相对于传统的将每个独立的对象进行一对一的编码。独热编码器可以将“一键编码”视为一种可以强化特征向量的工具。它查看每个功能并标识不同值的总数。它使用N分之一的方案来编码值。基于该方案对特征向量中的每个特征进行编码。这有助于我们提高空间效率。

关于“独热”的理解:经过编码后,一行数据中,只有一个数据是1,其余的都是0,对比红路灯,在一个时刻,该指示灯只能显示一种颜色

6.2 实例操作
给出举例数据
data = np.array([[1, 1, 2], [0, 2, 3], [1, 0, 1], [0, 1, 0]])
print(data)
输出的结果为:(可以发现共四行三列,假设这三列的名称分别为ABC,可以发现A中共有两个特征0和1,B中有三个特征,C中有四个特征)

那么接下来进行独热编码,根据上面的假设,经过独热编码后的结果应该有9个特征,前两个对应A字段,中间三个对应B字段,最后四个对应C字段,
encoder = preprocessing.OneHotEncoder()
encoder.fit(data)
encoder_vector = encoder.transform([[0,0,0]]).toarray()
print(encoder_vector)
encoder_vector = encoder.transform([[1,0,3]]).toarray()
print(encoder_vector)
输出结果为:(这里以[[0,0,0]]举例,A中两个特征0在前面第一个位置,B中三个特征,0在第一个位置,C中三个特征,0也在第一个位置。对比这种位置关系[[1,0,3]]独热编码后就不难理解了)

如果数字觉得冲突不好理解的话,那这里进行张三李四带入
data = np.array([['张三', '张三', '李四'], ['王五', '李四', '赵六'], ['张三', '王五', '张三'], ['王五','张三', '王五']])
print(data)
encoder = preprocessing.OneHotEncoder()
encoder.fit(data)
encoder_vector = encoder.transform([['张三','张三','张三']]).toarray()
print(encoder_vector)
输出结果为:(这里就和上面是一个原理,只不过才有中文文本数据进行展示,方便理解)

七、标签编码
7.1 标签编码定义
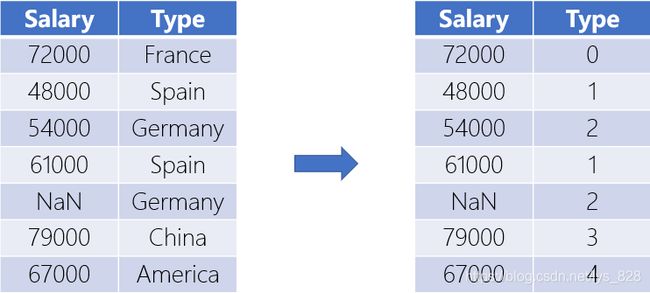
通常对于计算机直接无法识别文本数据,直接转换成为连续的数值型变量。即对于不连续的数字或者文本进行编号。常见的称呼就是给数据“贴标签”和找标签对应的数据。也可以手动操作,参考快速贴标签和找标签对应的数据
7.2 实例操作
也可以直接使用封装好的工具包,数据以几种车型为例
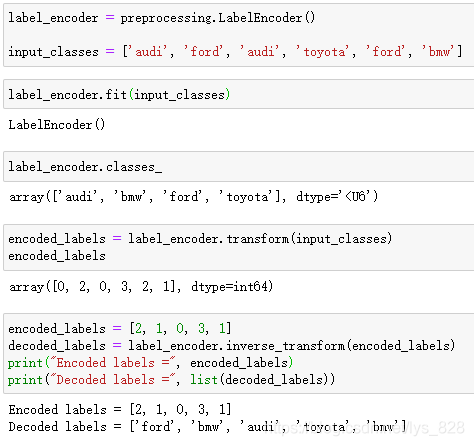
label_encoder = preprocessing.LabelEncoder()
input_classes = ['audi', 'ford', 'audi', 'toyota', 'ford', 'bmw']
label_encoder.fit(input_classes)
label_encoder.classes_
encoded_labels = label_encoder.transform(input_classes)
encoded_labels
#查看一下标签和数据的对应关系(反向)
encoded_labels = [2, 1, 0, 3, 1]
decoded_labels = label_encoder.inverse_transform(encoded_labels)
print("Encoded labels =", encoded_labels)
print("Decoded labels =", list(decoded_labels))
输出结果为:(除了正向编码,在进行fit后,还可以进行逆向编码,方便进行标签和数据之间的对应关系查看)
至此,整个大数据预处理的相关部分已经全部梳理完毕了,完结撒花✿✿ヽ(°▽°)ノ✿✿
总结
本文进行了大数据处理之前的准备工作的各个部分知识点的系统梳理,主要包含缺失值处理,数据标准化,0-1缩放,归一化,二值化和编码相关的问题,希望大家看完之后,能有所帮助,大数据系列后面有空会持续更新~
未完,待续!
