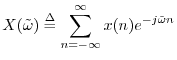快速傅里叶变换 python_短时傅里叶变换(Short Time Fourier Transform)原理及 Python 实现...

原理

短时傅里叶变换(Short Time Fourier Transform, STFT) 是一个用于语音信号处理的通用工具.它定义了一个非常有用的时间和频率分布类, 其指定了任意信号随时间和频率变化的复数幅度. 实际上,计算短时傅里叶变换的过程是把一个较长的时间信号分成相同长度的更短的段, 在每个更短的段上计算傅里叶变换, 即傅里叶频谱.

短时傅里叶变换通常的数学定义如下:

其中,

DTFT (Decrete Time Fourier Transform) 为离散时间傅里叶变换. 其数学公式, 如下所示:

其中, x(n) 为在采样数 n 处的信号幅度. ω~ 的定义如下:

实现时, 短时傅里叶变换被计算为一系列加窗数据帧的快速傅里叶变换 (Fast Fourier Transform, FFT)，其中窗口随时间 “滑动” (slide) 或“跳跃” (hop) 。

Python 实现

在程序中, frame_size 为将信号分为较短的帧的大小, 在语音处理中, 通常帧大小在 20ms 到 40ms 之间. 这里设置为 25ms, 即 frame_size = 0.025;

frame_stride 为相邻帧的滑动尺寸或跳跃尺寸, 通常帧的滑动尺寸在 10ms 到 20ms 之间, 这里设置为 10ms, 即 frame_stride = 0.01. 此时, 相邻帧的交叠大小为 15ms;

窗函数采用汉明窗函数 (Hamming Function) ;

在每一帧, 进行 512 点快速傅里叶变换, 即 NFFT = 512. 具体程序如下:

# -*- coding: utf8 -*-

import numpy as np

def calc_stft(signal, sample_rate=16000, frame_size=0.025, frame_stride=0.01, winfunc=np.hamming, NFFT=512):

# Calculate the number of frames from the signal

frame_length = frame_size * sample_rate

frame_step = frame_stride * sample_rate

signal_length = len(signal)

frame_length = int(round(frame_length))

frame_step = int(round(frame_step))

num_frames = 1 + int(np.ceil(float(np.abs(signal_length - frame_length)) / frame_step))

# zero padding

pad_signal_length = num_frames * frame_step + frame_length

z = np.zeros((pad_signal_length - signal_length))

# Pad signal to make sure that all frames have equal number of samples

# without truncating any samples from the original signal

pad_signal = np.append(signal, z)

# Slice the signal into frames from indices

indices = np.tile(np.arange(0, frame_length), (num_frames, 1)) + \

np.tile(np.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T

frames = pad_signal[indices.astype(np.int32, copy=False)]

# Get windowed frames

frames *= winfunc(frame_length)

# Compute the one-dimensional n-point discrete Fourier Transform(DFT) of

# a real-valued array by means of an efficient algorithm called Fast Fourier Transform (FFT)

mag_frames = np.absolute(np.fft.rfft(frames, NFFT))

# Compute power spectrum

pow_frames = (1.0 / NFFT) * ((mag_frames) ** 2)

return pow_frames

if __name__ == '__main__':

import scipy.io.wavfile

import matplotlib.pyplot as plt

# Read wav file

# "OSR_us_000_0010_8k.wav" is downloaded from http://www.voiptroubleshooter.com/open_speech/american.html

sample_rate, signal = scipy.io.wavfile.read("OSR_us_000_0010_8k.wav")

# Get speech data in the first 2 seconds

signal = signal[0:int(2. * sample_rate)]

# Calculate the short time fourier transform

pow_spec = calc_stft(signal, sample_rate)

plt.imshow(pow_spec)

plt.tight_layout()

plt.show()

参考资料

1. DISCRETE TIME FOURIER TRANSFORM (DTFT). https://www.dsprelated.com/freebooks/mdft/Discrete_Time_Fourier_Transform.html

2. THE SHORT-TIME FOURIER TRANSFORM. https://www.dsprelated.com/freebooks/sasp/Short_Time_Fourier_Transform.html

3. Short-time Fourier transform. https://en.wikipedia.org/wiki/Short-time_Fourier_transform

4. Speech Processing for Machine Learning: Filter banks, Mel-Frequency Cepstral Coefficients (MFCCs) and What's In-Between. https://haythamfayek.com/2016/04/21/speech-processing-for-machine-learning.html

Python scipy 计算短时傅里叶变换（Short-time Fourier transforms)

计算短时傅里叶变换(STFT) scipy.signal.stft(x,fs = 1.0,window ='hann',nperseg = 256,noverlap = None,nfft = Non ...

matlab 时频分析（短时傅里叶变换、STFT）

短时傅里叶变换,short-time fourier transformation,有时也叫加窗傅里叶变换,时间窗口使得信号只在某一小区间内有效,这就避免了传统的傅里叶变换在时频局部表达能力上的不足, ...

傅里叶变换 - Fourier Transform

傅里叶级数 傅里叶在他的专著<热的解析理论>中提出,任何一个周期函数都可以表示为若干个正弦函数的和,即: \[f(t)=a_0+\sum_{n=1}^{\infty}(a_ncos(n\o ...

「学习笔记」Fast Fourier Transform

前言 快速傅里叶变换(\(\text{Fast Fourier Transform,FFT}\) )是一种能在\(O(n \log n)\)的时间内完成多项式乘法的算法,在\(OI\)中的应用很多,是 ...

浅谈范德蒙德(Vandermonde)方阵的逆矩阵的求法以及快速傅里叶变换(FFT)中IDFT的原理

浅谈范德蒙德(Vandermonde)方阵的逆矩阵与拉格朗日(Lagrange)插值的关系以及快速傅里叶变换(FFT)中IDFT的原理 标签: 行列式 矩阵 线性代数 FFT 拉格朗日插值 只要稍微看 ...

短网址(short URL)系统的原理及其实现

短网址(short URL)系统的原理及其实现 https://hufangyun.com/2017/short-url/?hmsr=toutiao.io&utm_medium=toutiao ...

paip.编程语言方法重载实现的原理及python,php,js中实现方法重载

paip.编程语言方法重载实现的原理及python,php,js中实现方法重载 有些语言,在方法的重载上,形式上不支持函数重载,但可以通过模拟实现.. 主要原理:根据参数个数进行重载,或者使用默认值 ...

MapReduce 原理与 Python 实践

MapReduce 原理与 Python 实践 1. MapReduce 原理 以下是个人在MongoDB和Redis实际应用中总结的Map-Reduce的理解 Hadoop 的 MapReduce ...

随机推荐

[C#].NET中几种Timer的使用

这篇博客将梳理一下.NET中4个Timer类,及其用法. 1. System.Threading.Timer public Timer(TimerCallback callback, object s ...

[BZOJ1131][POI2008] Sta 树的深度

Description 给出一个N个点的树,找出一个点来,以这个点为根的树时,所有点的深度之和最大 Input 给出一个数字N,代表有N个点.N<=1000000 下面N-1条边. Output ...

C#_简单实用的翻页

简单实用的生成翻页HTML辅助类 C# using System.Text; namespace ClassLibrary { /// /// /// ...

Equivalent Strings

Equivalent Strings 题目链接:http://acm.hust.edu.cn/vjudge/contest/view.action?cid=84562#problem/E 题意: 给出 ...

IIS-Server is too busy _解决方法

httpRuntime Server Too Busy 修改方法:修改服务器.net配置“machine.config＂文件,该文件位于Windows系统目录下,如“C:\WINDOWS \Micro ...

（译）详解javascript立即执行函数表达式（IIFE）

写在前面 这是一篇译文,原文:Immediately-Invoked Function Expression (IIFE) 原文是一篇很经典的讲解IIFE的文章,很适合收藏.本文虽然是译文,但是直译的 ...

ubuntu启动慢

http://blog.sina.com.cn/s/blog_4cc9ffbc0100rxhh.html 参考 笔记本装的是ubuntu12.04,最近发现开机启动特别慢,至少3分钟,总担心系统会启动 ...

POJ 1325、ZOJ 1364、HDU 1150 Machine Schedule - from lanshui_Yang

Problem Description As we all know, machine scheduling is a very classical problem in computer scien ...

一个简单的redis调用类

能只能判断函数的调用规则,容错规则, 例如set函数 set($key, $value, $time = false) 根据time的真假来判断是否使用set,或者是setex函数 get函数 get ...

oracle修改字符集后数据库不能启动

最近在做修改字符集的实验,悲剧的是修改后重启,数据库启动不了. SQL> alter system set nls_language='AMERICAN'   scope = spfile; S ...