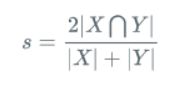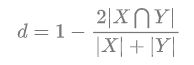Dice系数(Dice coefficient)与mIoU与Dice Loss
Dice系数和mIoU是语义分割的评价指标,在这里进行了简单知识介绍。讲到了Dice顺便在最后提一下Dice Loss,以后有时间区分一下在语义分割中两个常用的损失函数,交叉熵和Dice Loss。
一、Dice系数
1.概念理解
Dice系数是一种集合相似度度量函数,通常用于计算两个样本的相似度,取值范围在[0,1]:
其中X为预测像素,Y为groud truth,实际上,这和mIOU的定义差不多,仔细分析即可知道这个Dice等价于TP/(TP+FP+FN+TN)? https://blog.csdn.net/qq_35985044/article/details/104341058
其中 |X∩Y| 是X和Y之间的交集,|X|和|Y|分表表示X和Y的元素的个数,其中,分子的系数为2,是因为分母存在重复计算X和Y之间的共同元素的原因。
对于语义分割问题而言,X-GT分割图像(Ground Truth),Y-Pred分割图像
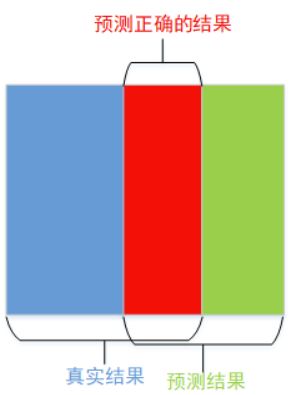
看图一直观理解一下
公式就可以理解为
2.实际计算
首先将 |X∩Y| 近似为预测图pred和label GT 之间的点乘,并将点乘的元素的结果相加:
(1)预测分割图与 GT 分割图的点乘:
(2)逐元素相乘的结果元素的相加和:
对于二分类问题,GT分割图是只有0,1两个值的,因此 |X∩Y| 可以有效的将在 Pred 分割图中未在 GT 分割图中激活的所有像素清零. 对于激活的像素,主要是惩罚低置信度的预测,较高值会得到更好的 Dice 系数.
(3)计算|X|和|Y|,这里可以采用直接元素相加,也可以采用元素平方求和的方法:
3.PyTorch代码
def dice_coeff(pred, target):
smooth = 1.
num = pred.size(0)
m1 = pred.view(num, -1) # Flatten
m2 = target.view(num, -1) # Flatten
intersection = (m1 * m2).sum()
return (2. * intersection + smooth) / (m1.sum() + m2.sum() + smooth)
二、mIoU
1.语义分割元素分类的四种情况
true positive(TP):预测正确, 预测结果是正类, 真实是正类
false positive(FP):预测错误, 预测结果是正类, 真实是负类
true negative(TN):预测错误, 预测结果是负类, 真实是正类
false negative(FN):预测正确, 预测结果是负类, 真实是负类
2.mIoU定义与单个IoU理解
计算真实值和预测值两个集合的交集和并集之比。这个比例可以变形为TP(交集)比上TP、FP、FN之和(并集)。即:mIoU=TP/(FP+FN+TP)。
这里还是直接上个图理解一下,详细解释看图二,我觉得讲的非常棒了。
对于pascal数据集来说, 对于21个类别, 分别求IoU:
对于某一个类别的IoU计算公式如下:
mIoU:计算两圆交集(橙色部分)与两圆并集(红色+橙色+黄色)之间的比例,理想情况下两圆重合,比例为1。
3.mIoU计算
(1)首先是计算混淆矩阵(误差矩阵)
(2)计算mIoU
这里代码比较多,以后有时间单独拿出来。也可以参考这个链接中的代码部分:https://blog.csdn.net/u012370185/article/details/94409933
以及这个github:https://github.com/dilligencer-zrj/code_zoo/blob/master/compute_mIOU
三、Dice Loss
Dice Loss的计算公式非常简单如下:
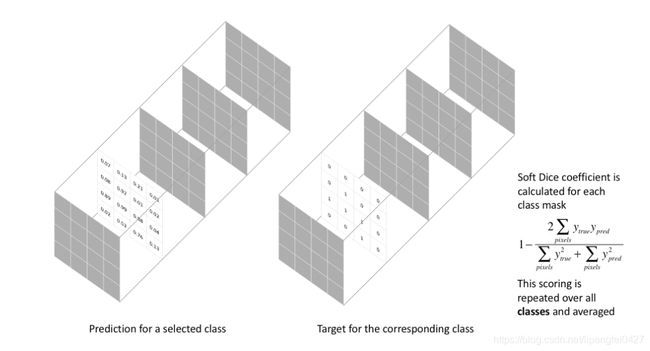
这种损失函数被称为 Soft Dice Loss,因为我们直接使用预测概率而不是使用阈值或将它们转换为二进制mask。
Soft Dice Loss 将每个类别分开考虑,然后平均得到最后结果。比较直观如图三所示。
需要注意的是Dice Loss存在两个问题:
(1)训练误差曲线非常混乱,很难看出关于收敛的信息。尽管可以检查在验证集上的误差来避开此问题。
(2)Dice Loss比较适用于样本极度不均的情况,一般的情况下,使用 Dice Loss 会对反向传播造成不利的影响,容易使训练变得不稳定。
所以在一般情况下,还是使用交叉熵损失函数。
PyTorch参考代码
import torch.nn as nn
import torch.nn.functional as F
class SoftDiceLoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(SoftDiceLoss, self).__init__()
def forward(self, logits, targets):
num = targets.size(0)
smooth = 1
probs = F.sigmoid(logits)
m1 = probs.view(num, -1)
m2 = targets.view(num, -1)
intersection = (m1 * m2)
score = 2. * (intersection.sum(1) + smooth) / (m1.sum(1) + m2.sum(1) + smooth)
score = 1 - score.sum() / num
return score
参考链接:
https://zhuanlan.zhihu.com/p/86704421
https://blog.csdn.net/weixin_43346901/article/details/99880278?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~all~baidu_landing_v2~default-1-99880278.nonecase&utm_term=mi%E4%B8%8Edice&spm=1000.2123.3001.4430
https://blog.csdn.net/gjk0223/article/details/2314844
https://blog.csdn.net/Biyoner/article/details/84728417
https://www.aiuai.cn/aifarm1159.html
https://zhuanlan.zhihu.com/p/88805121
https://blog.csdn.net/u012370185/article/details/94409933