浅谈机器学习之批量梯度下降
浅谈机器学习之批量梯度下降
- 机器学习
-
- 机器学习和人工学习
- 机器学习分类
- 回归和分类
- 连续变量和离散变量
- 机器学习三要素
-
- 模型
- 策略
- 算法
- 梯度下降方法
- 方法1
- 方法2
-
-
-
-
- 以上方法采用的是批量梯度下降的方法
-
-
-
- 梯度下降的方式还有随机梯度下降方法和小批量梯度下降的方法
机器学习
机器学习是一门多领域交叉学科,涉及概率论、统计学、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。为了解决任务T,设计一段程序,从经验E中学习达到性能度量值P,当且仅当有了经验E后,经过P评判,程序在处理T时的性能得到提升
机器学习和人工学习
通过实际的例子可能更好的理解,为了解决一个人感冒的问题,医生会根据以往的经验,评判病人 的病情状况,而机器学习,是输入病人的病情状况,学习大量的以往数据,选择合适的模型,再通过评判标准P得出病人的状况
机器学习分类
1.有监督的学习,包括:回归,分类
2.无监督的学习,包括:聚类,降纬
3.强化学习,包括:有模型学习,无模型学习
有监督学习和无监督学习的区别在与有没有标签
回归和分类
回归:样本的标签属于连续变量
分类:样本的标签属于离散变量
连续变量和离散变量
连续变量:可以从任意取值的变量叫连续变量
离散变量:如:性别,教育程度等.
机器学习三要素
模型
就是要学习的概率分布或决策函数
策略
适合解决某一种问题有很多种的模型,我们把这种模型称为:假设空间
我们从假设空间里选取一个最优的模型方法成为策略
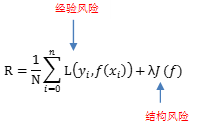
怎么选取一个最优的方法呢?我们通过损失函数的方式来判断,当损失函数最小时候,这个方法就是最优的方法.记作L(Y,f(x)).通常的损失函数有如下几种方式:
1.0-1损失函数
也就是将数据进行0,1标准化,公式为:(x-x的均值)/x的标准差.
2.平方损失函数
3.绝对损失函数
4.对数损失函数
算法
算法是指学习模型时的具体计算方法,求解最优模型归结为一个最优化问题,统计学习方法的算法等价于求最优化问题的方法也就是求解析解,或者数值解
梯度下降方法
1.定义:
用函数求最小值的算法
2.思想
随机选择一个参数组合 ( Θ 0 , Θ 1 , Θ 2 , Θ 3 , ⋯ , Θ n ) (\Theta{\atop 0},\Theta{\atop 1},\Theta{\atop 2},\Theta{\atop 3}, \cdots ,\Theta{\atop n}) (Θ0,Θ1,Θ2,Θ3,⋯,Θn),计算代价函数
寻找下一个能让代价函数值最低的函数组合
持续找到一个局部最小值
(由于没有对比全局,这个局部变量最小值不能确定是全局最小值)
3.选定模型
h Θ ( x ) = Θ 0 + Θ 1 x h{\atop \Theta}(x) =\Theta{\atop 0}+\Theta{\atop 1}x hΘ(x)=Θ0+Θ1x
J ( Θ 0 , Θ 1 ) = 1 2 m lim i = 1 M ( h 0 ( x ( i ) ) − y ( ( i ) ) ) 2 J(\Theta{\atop 0},\Theta{\atop 1})=\frac{1}{2m}\displaystyle \lim^{M}_{i=1}{(h{\atop0 }(x^{(i)}) -y(^{(i)}))^2} J(Θ0,Θ1)=2m1i=1limM(h0(x(i))−y((i)))2
Θ 1 = Θ 1 − α δ J ( Θ ) δ ( Θ 1 ) \Theta{\atop 1}=\Theta{\atop 1}-\alpha\frac{\delta J(\Theta)}{\delta (\Theta{\atop 1})} Θ1=Θ1−αδ(Θ1)δJ(Θ)
4.用代码实现
// 导入numpy包
import numpy as np
// 定义原函数
def f(x):
return x**2-4*x+4
// 导数函数
def h(x):
return x*2-4
方法1
// 1.用距离步长改变的方法.直到距离趋近0.我们这里选取的是10^(-10)
# 初始点
a =16
# 步长
step = 0.1
# 计数
count = 0
# a更新前后的差值(初始值设置为起始点)就是横坐标改变的差值,差值一直改变直到不能再改变为止
deta_a = 16
# 给定的阀值
error_rate = 1e-20
# 当a每次减小固定的值后,如果在e的负10次方
while deta_a>error_rate:
a = a -step * h(a)
deta_a = np.abs(deta_a - a)
count +=1
print("梯度下降迭代第{}次,原始值为{},极点值为{}".format(count, a, f(a)))
print('迭代次数%d'%count)
print('极值点为(%f,%f)'%(a,f(a)))
方法2
// 2.用斜率的方法.直到斜率趋近0.我们这里选取的是10^(-10)
# 初始点
a =16
# 步长
step = 0.05
# 计数
count = 0
# 给定的阀值
error_rate = 1e-10
# 初始斜率
k =np.abs(h(16))
# 当a每次减小固定的值后,如果在e的负10次方
while k>error_rate:
a = a -step * h(a)
k = h(a)
count +=1
print("梯度下降迭代第{}次,原始值为{},极点值为{}".format(count, a, f(a)))
print('迭代次数%d'%count)
print('极值点为(%f,%f)'%(a,f(a)))
以上方法采用的是批量梯度下降的方法
梯度下降的方式还有随机梯度下降方法和小批量梯度下降的方法
批量梯度下降的方式是沿着 ( Θ 0 , Θ 1 ) (\Theta{\atop 0},\Theta{\atop 1}) (Θ0,Θ1)各自求导的方式,朝着导数为0的方向找到最优值,而速度比较慢,随机梯度下降的方式优点是速度比较快,但是找寻最优解的方式是不确定的,小批量梯度下降的方式是集合了两者的优点,也是目前用的最多方法之一