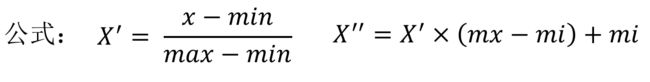ninjawei

机器学习-第三方库(工具包)-scikit-learn【特征工程】

Python语言的机器学习工具
Scikit-learn包括许多知名的机器学习算法的实现(算法原理一定要懂)
Scikit-learn文档完善，容易上手，封装的好，丰富的API，建立模型简单，预测简单，使其在学术界颇受欢迎。
Scikit-learn缺点：算法过程无法看到，有些参数都在算法Api内部优化，无法手动调参。(相对比的，tensorflow的Api有的封装的高，有的封装的低，可以手动调参。比如Scikit-learn的线性回归梯度下降法无法手动调α学习率大小，而tensorflow可以手动调节)

一、scikit-learn数据集

1、scikit-learn获取数据集

sklearn.datasets是scikit-learn获取数据集的api，加载获取流行数据集
load和fetch返回的数据类型datasets.base.Bunch(字典格式)

data：特征数据数组，是 [n_samples * n_features] 的二维numpy.ndarray 数组
target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
DESCR：数据描述
feature_names：特征名,新闻数据，手写数字、回归数据集没有
target_names：标签名,回归数据集没有

1.1 sklearn.datasets.load_*()

获取小规模数据集，数据在\sklearn\datasets\data目录里，下载scikit-learn时同时下载下来了；

1.1.1 sklearn分类数据集(目标值是离散型的)

1.1.1.1 “鸢尾花分类” 数据集

sklearn.datasets.load_iris()

from sklearn.datasets import load_iris

li = load_iris()
print("特征值---->li.feature_names = \n", li.feature_names)
print("签名值---->li.target_names = \n", li.target_names)
print("目标值---->li.target = \n", li.target)
print("特征数据数组---->li.data = \n", li.data)
print('数据描述---->li.DESCR = \n', li.DESCR)

打印结果

特征值---->li.feature_names = 
 ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
签名值---->li.target_names = 
 ['setosa' 'versicolor' 'virginica']
目标值---->li.target = 
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
特征数据数组---->li.data = 
 [[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]
 [5.4 3.9 1.7 0.4]
 [4.6 3.4 1.4 0.3]
 [5.  3.4 1.5 0.2]
 [4.4 2.9 1.4 0.2]
 [4.9 3.1 1.5 0.1]
 [5.4 3.7 1.5 0.2]
 [4.8 3.4 1.6 0.2]
 [4.8 3.  1.4 0.1]
 [4.3 3.  1.1 0.1]
 [5.8 4.  1.2 0.2]
 [5.7 4.4 1.5 0.4]
 [5.4 3.9 1.3 0.4]
 [5.1 3.5 1.4 0.3]
 [5.7 3.8 1.7 0.3]
 [5.1 3.8 1.5 0.3]
 [5.4 3.4 1.7 0.2]
 [5.1 3.7 1.5 0.4]
 [4.6 3.6 1.  0.2]
 [5.1 3.3 1.7 0.5]
 [4.8 3.4 1.9 0.2]
 [5.  3.  1.6 0.2]
 [5.  3.4 1.6 0.4]
 [5.2 3.5 1.5 0.2]
 [5.2 3.4 1.4 0.2]
 [4.7 3.2 1.6 0.2]
 [4.8 3.1 1.6 0.2]
 [5.4 3.4 1.5 0.4]
 [5.2 4.1 1.5 0.1]
 [5.5 4.2 1.4 0.2]
 [4.9 3.1 1.5 0.1]
 [5.  3.2 1.2 0.2]
 [5.5 3.5 1.3 0.2]
 [4.9 3.1 1.5 0.1]
 [4.4 3.  1.3 0.2]
 [5.1 3.4 1.5 0.2]
 [5.  3.5 1.3 0.3]
 [4.5 2.3 1.3 0.3]
 [4.4 3.2 1.3 0.2]
 [5.  3.5 1.6 0.6]
 [5.1 3.8 1.9 0.4]
 [4.8 3.  1.4 0.3]
 [5.1 3.8 1.6 0.2]
 [4.6 3.2 1.4 0.2]
 [5.3 3.7 1.5 0.2]
 [5.  3.3 1.4 0.2]
 [7.  3.2 4.7 1.4]
 [6.4 3.2 4.5 1.5]
 [6.9 3.1 4.9 1.5]
 [5.5 2.3 4.  1.3]
 [6.5 2.8 4.6 1.5]
 [5.7 2.8 4.5 1.3]
 [6.3 3.3 4.7 1.6]
 [4.9 2.4 3.3 1. ]
 [6.6 2.9 4.6 1.3]
 [5.2 2.7 3.9 1.4]
 [5.  2.  3.5 1. ]
 [5.9 3.  4.2 1.5]
 [6.  2.2 4.  1. ]
 [6.1 2.9 4.7 1.4]
 [5.6 2.9 3.6 1.3]
 [6.7 3.1 4.4 1.4]
 [5.6 3.  4.5 1.5]
 [5.8 2.7 4.1 1. ]
 [6.2 2.2 4.5 1.5]
 [5.6 2.5 3.9 1.1]
 [5.9 3.2 4.8 1.8]
 [6.1 2.8 4.  1.3]
 [6.3 2.5 4.9 1.5]
 [6.1 2.8 4.7 1.2]
 [6.4 2.9 4.3 1.3]
 [6.6 3.  4.4 1.4]
 [6.8 2.8 4.8 1.4]
 [6.7 3.  5.  1.7]
 [6.  2.9 4.5 1.5]
 [5.7 2.6 3.5 1. ]
 [5.5 2.4 3.8 1.1]
 [5.5 2.4 3.7 1. ]
 [5.8 2.7 3.9 1.2]
 [6.  2.7 5.1 1.6]
 [5.4 3.  4.5 1.5]
 [6.  3.4 4.5 1.6]
 [6.7 3.1 4.7 1.5]
 [6.3 2.3 4.4 1.3]
 [5.6 3.  4.1 1.3]
 [5.5 2.5 4.  1.3]
 [5.5 2.6 4.4 1.2]
 [6.1 3.  4.6 1.4]
 [5.8 2.6 4.  1.2]
 [5.  2.3 3.3 1. ]
 [5.6 2.7 4.2 1.3]
 [5.7 3.  4.2 1.2]
 [5.7 2.9 4.2 1.3]
 [6.2 2.9 4.3 1.3]
 [5.1 2.5 3.  1.1]
 [5.7 2.8 4.1 1.3]
 [6.3 3.3 6.  2.5]
 [5.8 2.7 5.1 1.9]
 [7.1 3.  5.9 2.1]
 [6.3 2.9 5.6 1.8]
 [6.5 3.  5.8 2.2]
 [7.6 3.  6.6 2.1]
 [4.9 2.5 4.5 1.7]
 [7.3 2.9 6.3 1.8]
 [6.7 2.5 5.8 1.8]
 [7.2 3.6 6.1 2.5]
 [6.5 3.2 5.1 2. ]
 [6.4 2.7 5.3 1.9]
 [6.8 3.  5.5 2.1]
 [5.7 2.5 5.  2. ]
 [5.8 2.8 5.1 2.4]
 [6.4 3.2 5.3 2.3]
 [6.5 3.  5.5 1.8]
 [7.7 3.8 6.7 2.2]
 [7.7 2.6 6.9 2.3]
 [6.  2.2 5.  1.5]
 [6.9 3.2 5.7 2.3]
 [5.6 2.8 4.9 2. ]
 [7.7 2.8 6.7 2. ]
 [6.3 2.7 4.9 1.8]
 [6.7 3.3 5.7 2.1]
 [7.2 3.2 6.  1.8]
 [6.2 2.8 4.8 1.8]
 [6.1 3.  4.9 1.8]
 [6.4 2.8 5.6 2.1]
 [7.2 3.  5.8 1.6]
 [7.4 2.8 6.1 1.9]
 [7.9 3.8 6.4 2. ]
 [6.4 2.8 5.6 2.2]
 [6.3 2.8 5.1 1.5]
 [6.1 2.6 5.6 1.4]
 [7.7 3.  6.1 2.3]
 [6.3 3.4 5.6 2.4]
 [6.4 3.1 5.5 1.8]
 [6.  3.  4.8 1.8]
 [6.9 3.1 5.4 2.1]
 [6.7 3.1 5.6 2.4]
 [6.9 3.1 5.1 2.3]
 [5.8 2.7 5.1 1.9]
 [6.8 3.2 5.9 2.3]
 [6.7 3.3 5.7 2.5]
 [6.7 3.  5.2 2.3]
 [6.3 2.5 5.  1.9]
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]
数据描述---->li.DESCR = 
 Iris Plants Database
====================
Notes
-----
Data Set Characteristics:
    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
    :Summary Statistics:
    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20  0.76     0.9565  (high!)
    ============== ==== ==== ======= ===== ====================
    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988
This is a copy of UCI ML iris datasets.
http://archive.ics.uci.edu/ml/datasets/Iris
The famous Iris database, first used by Sir R.A Fisher
This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
References
----------
   - Fisher,R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

1.1.1.2 “数字分类” 数据集

sklearn.datasets.load_digits()

from sklearn.datasets import load_digits

li = load_digits()
print("签名值---->li.target_names = \n", li.target_names)
print("目标值---->li.target = \n", li.target)
print("特征数据数组---->li.data = \n", li.data)
print('数据描述---->li.DESCR = \n', li.DESCR)

打印结果：

签名值---->li.target_names = 
 [0 1 2 3 4 5 6 7 8 9]
目标值---->li.target = 
 [0 1 2 ... 8 9 8]
特征数据数组---->li.data = 
 [[ 0.  0.  5. ...  0.  0.  0.]
 [ 0.  0.  0. ... 10.  0.  0.]
 [ 0.  0.  0. ... 16.  9.  0.]
 ...
 [ 0.  0.  1. ...  6.  0.  0.]
 [ 0.  0.  2. ... 12.  0.  0.]
 [ 0.  0. 10. ... 12.  1.  0.]]
数据描述---->li.DESCR = 
 Optical Recognition of Handwritten Digits Data Set
===================================================
Notes
-----
Data Set Characteristics:
    :Number of Instances: 5620
    :Number of Attributes: 64
    :Attribute Information: 8x8 image of integer pixels in the range 0..16.
    :Missing Attribute Values: None
    :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
    :Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets
http://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.
Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.
References
----------
  - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
    Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
    Graduate Studies in Science and Engineering, Bogazici University.
  - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
  - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
    Linear dimensionalityreduction using relevance weighted LDA. School of
    Electrical and Electronic Engineering Nanyang Technological University.
    2005.
  - Claudio Gentile. A New Approximate Maximal Margin Classification
    Algorithm. NIPS. 2000.

1.1.1.3 “20Newsgroups” 数据集

sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)
用于分类的大数据集
subset: ‘train’或者’test’,‘all’，可选，选择要加载的数据集：训练集的“训练”，测试集的“测试”，两者的“全部”，一般选择’all’，然后手动用split来划分训练集与测试集。
datasets.clear_data_home(data_home=None)：清除目录下的数据

from sklearn.datasets import fetch_20newsgroups

news = fetch_20newsgroups(subset='all')
print("特征数据值数组中的第一个---->news.data[0] = \n", news.data[0])
print("签名值---->news.target_names = \n", news.target_names)
print("目标值---->news.target = ", news.target)
print('数据描述---->news.description = ', news.description)

打印结果：

特征数据值数组中的第一个---->news.data[0] = 
 From: Mamatha Devineni Ratnam <mr47+@andrew.cmu.edu>
Subject: Pens fans reactions
Organization: Post Office, Carnegie Mellon, Pittsburgh, PA
Lines: 12
NNTP-Posting-Host: po4.andrew.cmu.edu
I am sure some bashers of Pens fans are pretty confused about the lack
of any kind of posts about the recent Pens massacre of the Devils. Actually,
I am  bit puzzled too and a bit relieved. However, I am going to put an end
to non-PIttsburghers' relief with a bit of praise for the Pens. Man, they
are killing those Devils worse than I thought. Jagr just showed you why
he is much better than his regular season stats. He is also a lot
fo fun to watch in the playoffs. Bowman should let JAgr have a lot of
fun in the next couple of games since the Pens are going to beat the pulp out of Jersey anyway. I was very disappointed not to see the Islanders lose the final
regular season game.          PENS RULE!!!
签名值---->news.target_names = 
 ['alt.atheism', 'comp.graphics', 'comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware', 'comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale', 'rec.autos', 'rec.motorcycles', 'rec.sport.baseball', 'rec.sport.hockey', 'sci.crypt', 'sci.electronics', 'sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns', 'talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc']
目标值---->news.target =  [10  3 17 ...  3  1  7]
数据描述---->news.description =  the 20 newsgroups by date dataset

1.1.2 sklearn回归数据集(目标值是连续型的)

1.1.2.1 ：“波士顿房价” 数据集

sklearn.datasets.load_boston()

from sklearn.datasets import load_boston

lb = load_boston()

print("获取特征数据值 lb.data = \n", lb.data)
print("目标值 lb.target = \n", lb.target)
print('lb.DESCR = \n', lb.DESCR)

打印结果：

获取特征数据值 lb.data = 
 [[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]
 [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]
 [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]
 ...
 [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]
 [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]
 [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]
目标值 lb.target = 
 [24.  21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15.  18.9 21.7 20.4
 18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8
 18.4 21.  12.7 14.5 13.2 13.1 13.5 18.9 20.  21.  24.7 30.8 34.9 26.6
 25.3 24.7 21.2 19.3 20.  16.6 14.4 19.4 19.7 20.5 25.  23.4 18.9 35.4
 24.7 31.6 23.3 19.6 18.7 16.  22.2 25.  33.  23.5 19.4 22.  17.4 20.9
 24.2 21.7 22.8 23.4 24.1 21.4 20.  20.8 21.2 20.3 28.  23.9 24.8 22.9
 23.9 26.6 22.5 22.2 23.6 28.7 22.6 22.  22.9 25.  20.6 28.4 21.4 38.7
 43.8 33.2 27.5 26.5 18.6 19.3 20.1 19.5 19.5 20.4 19.8 19.4 21.7 22.8
 18.8 18.7 18.5 18.3 21.2 19.2 20.4 19.3 22.  20.3 20.5 17.3 18.8 21.4
 15.7 16.2 18.  14.3 19.2 19.6 23.  18.4 15.6 18.1 17.4 17.1 13.3 17.8
 14.  14.4 13.4 15.6 11.8 13.8 15.6 14.6 17.8 15.4 21.5 19.6 15.3 19.4
 17.  15.6 13.1 41.3 24.3 23.3 27.  50.  50.  50.  22.7 25.  50.  23.8
 23.8 22.3 17.4 19.1 23.1 23.6 22.6 29.4 23.2 24.6 29.9 37.2 39.8 36.2
 37.9 32.5 26.4 29.6 50.  32.  29.8 34.9 37.  30.5 36.4 31.1 29.1 50.
 33.3 30.3 34.6 34.9 32.9 24.1 42.3 48.5 50.  22.6 24.4 22.5 24.4 20.
 21.7 19.3 22.4 28.1 23.7 25.  23.3 28.7 21.5 23.  26.7 21.7 27.5 30.1
 44.8 50.  37.6 31.6 46.7 31.5 24.3 31.7 41.7 48.3 29.  24.  25.1 31.5
 23.7 23.3 22.  20.1 22.2 23.7 17.6 18.5 24.3 20.5 24.5 26.2 24.4 24.8
 29.6 42.8 21.9 20.9 44.  50.  36.  30.1 33.8 43.1 48.8 31.  36.5 22.8
 30.7 50.  43.5 20.7 21.1 25.2 24.4 35.2 32.4 32.  33.2 33.1 29.1 35.1
 45.4 35.4 46.  50.  32.2 22.  20.1 23.2 22.3 24.8 28.5 37.3 27.9 23.9
 21.7 28.6 27.1 20.3 22.5 29.  24.8 22.  26.4 33.1 36.1 28.4 33.4 28.2
 22.8 20.3 16.1 22.1 19.4 21.6 23.8 16.2 17.8 19.8 23.1 21.  23.8 23.1
 20.4 18.5 25.  24.6 23.  22.2 19.3 22.6 19.8 17.1 19.4 22.2 20.7 21.1
 19.5 18.5 20.6 19.  18.7 32.7 16.5 23.9 31.2 17.5 17.2 23.1 24.5 26.6
 22.9 24.1 18.6 30.1 18.2 20.6 17.8 21.7 22.7 22.6 25.  19.9 20.8 16.8
 21.9 27.5 21.9 23.1 50.  50.  50.  50.  50.  13.8 13.8 15.  13.9 13.3
 13.1 10.2 10.4 10.9 11.3 12.3  8.8  7.2 10.5  7.4 10.2 11.5 15.1 23.2
  9.7 13.8 12.7 13.1 12.5  8.5  5.   6.3  5.6  7.2 12.1  8.3  8.5  5.
 11.9 27.9 17.2 27.5 15.  17.2 17.9 16.3  7.   7.2  7.5 10.4  8.8  8.4
 16.7 14.2 20.8 13.4 11.7  8.3 10.2 10.9 11.   9.5 14.5 14.1 16.1 14.3
 11.7 13.4  9.6  8.7  8.4 12.8 10.5 17.1 18.4 15.4 10.8 11.8 14.9 12.6
 14.1 13.  13.4 15.2 16.1 17.8 14.9 14.1 12.7 13.5 14.9 20.  16.4 17.7
 19.5 20.2 21.4 19.9 19.  19.1 19.1 20.1 19.9 19.6 23.2 29.8 13.8 13.3
 16.7 12.  14.6 21.4 23.  23.7 25.  21.8 20.6 21.2 19.1 20.6 15.2  7.
  8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9
 22.  11.9]
lb.DESCR = 
 Boston House Prices dataset
===========================
Notes
------
Data Set Characteristics:  
    :Number of Instances: 506 
    :Number of Attributes: 13 numeric/categorical predictive
    
    :Median Value (attribute 14) is usually the target
    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's
    :Missing Attribute Values: None
    :Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
http://archive.ics.uci.edu/ml/datasets/Housing
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
', Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
**References**
   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
   - many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)

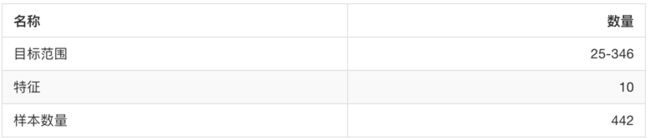
1.1.2.2 ：“糖尿病” 数据集

sklearn.datasets.load_diabetes()

from sklearn.datasets import load_diabetes

ld = load_diabetes()

print("获取特征数据值 ld.data = \n", ld.data)
print("目标值 ld.target = \n", ld.target)
print('ld.DESCR = \n', ld.DESCR)

打印结果：

获取特征数据值 ld.data = 
 [[ 0.03807591  0.05068012  0.06169621 ... -0.00259226  0.01990842
  -0.01764613]
 [-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974
  -0.09220405]
 [ 0.08529891  0.05068012  0.04445121 ... -0.00259226  0.00286377
  -0.02593034]
 ...
 [ 0.04170844  0.05068012 -0.01590626 ... -0.01107952 -0.04687948
   0.01549073]
 [-0.04547248 -0.04464164  0.03906215 ...  0.02655962  0.04452837
  -0.02593034]
 [-0.04547248 -0.04464164 -0.0730303  ... -0.03949338 -0.00421986
   0.00306441]]
目标值 ld.target = 
 [151.  75. 141. 206. 135.  97. 138.  63. 110. 310. 101.  69. 179. 185.
 118. 171. 166. 144.  97. 168.  68.  49.  68. 245. 184. 202. 137.  85.
 131. 283. 129.  59. 341.  87.  65. 102. 265. 276. 252.  90. 100.  55.
  61.  92. 259.  53. 190. 142.  75. 142. 155. 225.  59. 104. 182. 128.
  52.  37. 170. 170.  61. 144.  52. 128.  71. 163. 150.  97. 160. 178.
  48. 270. 202. 111.  85.  42. 170. 200. 252. 113. 143.  51.  52. 210.
  65. 141.  55. 134.  42. 111.  98. 164.  48.  96.  90. 162. 150. 279.
  92.  83. 128. 102. 302. 198.  95.  53. 134. 144. 232.  81. 104.  59.
 246. 297. 258. 229. 275. 281. 179. 200. 200. 173. 180.  84. 121. 161.
  99. 109. 115. 268. 274. 158. 107.  83. 103. 272.  85. 280. 336. 281.
 118. 317. 235.  60. 174. 259. 178. 128.  96. 126. 288.  88. 292.  71.
 197. 186.  25.  84.  96. 195.  53. 217. 172. 131. 214.  59.  70. 220.
 268. 152.  47.  74. 295. 101. 151. 127. 237. 225.  81. 151. 107.  64.
 138. 185. 265. 101. 137. 143. 141.  79. 292. 178.  91. 116.  86. 122.
  72. 129. 142.  90. 158.  39. 196. 222. 277.  99. 196. 202. 155.  77.
 191.  70.  73.  49.  65. 263. 248. 296. 214. 185.  78.  93. 252. 150.
  77. 208.  77. 108. 160.  53. 220. 154. 259.  90. 246. 124.  67.  72.
 257. 262. 275. 177.  71.  47. 187. 125.  78.  51. 258. 215. 303. 243.
  91. 150. 310. 153. 346.  63.  89.  50.  39. 103. 308. 116. 145.  74.
  45. 115. 264.  87. 202. 127. 182. 241.  66.  94. 283.  64. 102. 200.
 265.  94. 230. 181. 156. 233.  60. 219.  80.  68. 332. 248.  84. 200.
  55.  85.  89.  31. 129.  83. 275.  65. 198. 236. 253. 124.  44. 172.
 114. 142. 109. 180. 144. 163. 147.  97. 220. 190. 109. 191. 122. 230.
 242. 248. 249. 192. 131. 237.  78. 135. 244. 199. 270. 164.  72.  96.
 306.  91. 214.  95. 216. 263. 178. 113. 200. 139. 139.  88. 148.  88.
 243.  71.  77. 109. 272.  60.  54. 221.  90. 311. 281. 182. 321.  58.
 262. 206. 233. 242. 123. 167.  63. 197.  71. 168. 140. 217. 121. 235.
 245.  40.  52. 104. 132.  88.  69. 219.  72. 201. 110.  51. 277.  63.
 118.  69. 273. 258.  43. 198. 242. 232. 175.  93. 168. 275. 293. 281.
  72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257.  55.  84.  42.
 146. 212. 233.  91. 111. 152. 120.  67. 310.  94. 183.  66. 173.  72.
  49.  64.  48. 178. 104. 132. 220.  57.]
ld.DESCR = 
 Diabetes dataset
================
Notes
-----
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
Data Set Characteristics:
  :Number of Instances: 442
  :Number of Attributes: First 10 columns are numeric predictive values
  :Target: Column 11 is a quantitative measure of disease progression one year after baseline
  :Attributes:
    :Age:
    :Sex:
    :Body mass index:
    :Average blood pressure:
    :S1:
    :S2:
    :S3:
    :S4:
    :S5:
    :S6:
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).
Source URL:
http://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(http://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)

1.2 sklearn.datasets.fetch_*(data_home=None)

获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录,默认是 ~/scikit_learn_data/；windows系统默认保存位置为C:\Users\Admin\scikit_learn_data

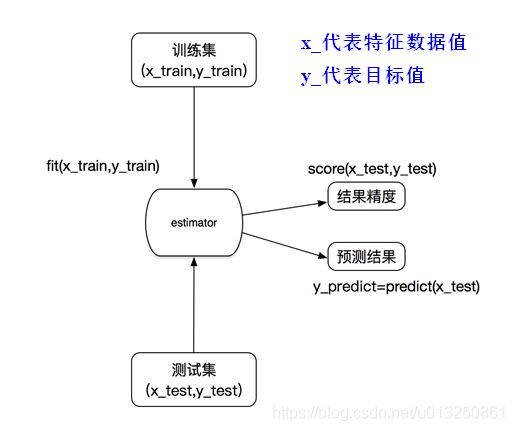
2、scikit-learn分割数据集

2.1 数据集划分原则

机器学习一般的数据集会划分为两个部分：

训练数据(75%)：用于训练，构建模型；
测试数据(25%)：在模型检验时使用，用于评估模型是否有效；

2.2 scikit-learn数据集分割API

sklearn.model_selection.train_test_split(arrays, options)
arrays表示可以传入多个array参数

x 数据集的特征数据值
y 数据集的目标值(标签值)

options 表示可以传入多个参数

test_size 测试集的大小，一般为float
random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。

return 返回值顺序

特征数据值of训练集, 特征数据值of测试集，目标值of训练集 , 目标值of测试集

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

li = load_iris()
# 注意返回值顺序： eigenvalues_train(特征数据值-训练集), eigenvalues_test(特征数据值-测试集)，target_value_train(目标值-训练集) , target_value_test(目标值-测试集)
eigenValuesOfTrainDataFrame, eigenValuesOfTestDataFrame, targetValuesOfTrainSeries, targetValuesOfTestSeries = train_test_split(li.data, li.target, test_size=0.25)

print('\n特征数据值of训练集 eigenValuesOfTrainDataFrame：\n', eigenValuesOfTrainDataFrame)
print('\n特征数据值of测试集 eigenValuesOfTestDataFrame：\n', eigenValuesOfTestDataFrame)
print('\n目标值of训练集 targetValuesOfTrainSeries：\n', targetValuesOfTrainSeries)
print('\n目标值of测试集 targetValuesOfTestSeries：\n', targetValuesOfTestSeries)

打印结果：

特征数据值of训练集 eigenValuesOfTrainDataFrame：
 [[5.7 4.4 1.5 0.4]
 [6.1 3.  4.6 1.4]
 [7.3 2.9 6.3 1.8]
 [7.7 2.8 6.7 2. ]
 [6.4 3.1 5.5 1.8]
 [5.5 2.5 4.  1.3]
 [5.6 3.  4.1 1.3]
 [5.6 2.9 3.6 1.3]
 [4.8 3.1 1.6 0.2]
 [5.  2.3 3.3 1. ]
 [5.  3.5 1.3 0.3]
 [4.7 3.2 1.6 0.2]
 [6.  2.7 5.1 1.6]
 [5.  3.4 1.6 0.4]
 [6.3 3.3 6.  2.5]
 [6.  2.2 4.  1. ]
 [5.  3.3 1.4 0.2]
 [6.1 2.9 4.7 1.4]
 [5.4 3.4 1.5 0.4]
 [7.2 3.  5.8 1.6]
 [6.7 3.3 5.7 2.5]
 [6.1 2.6 5.6 1.4]
 [4.8 3.4 1.6 0.2]
 [4.6 3.6 1.  0.2]
 [6.7 3.1 5.6 2.4]
 [6.4 3.2 5.3 2.3]
 [4.4 3.  1.3 0.2]
 [4.9 2.5 4.5 1.7]
 [6.1 3.  4.9 1.8]
 [6.8 2.8 4.8 1.4]
 [7.7 2.6 6.9 2.3]
 [6.3 2.5 4.9 1.5]
 [5.1 3.3 1.7 0.5]
 [6.9 3.2 5.7 2.3]
 [4.5 2.3 1.3 0.3]
 [7.4 2.8 6.1 1.9]
 [5.5 2.4 3.7 1. ]
 [5.  3.5 1.6 0.6]
 [7.9 3.8 6.4 2. ]
 [5.6 3.  4.5 1.5]
 [5.1 3.8 1.6 0.2]
 [6.5 3.  5.5 1.8]
 [6.7 2.5 5.8 1.8]
 [6.5 3.2 5.1 2. ]
 [4.3 3.  1.1 0.1]
 [5.7 2.9 4.2 1.3]
 [5.1 2.5 3.  1.1]
 [5.1 3.7 1.5 0.4]
 [5.5 2.3 4.  1.3]
 [5.5 3.5 1.3 0.2]
 [6.9 3.1 5.4 2.1]
 [5.4 3.  4.5 1.5]
 [5.4 3.4 1.7 0.2]
 [7.2 3.2 6.  1.8]
 [6.4 2.9 4.3 1.3]
 [7.6 3.  6.6 2.1]
 [5.  3.6 1.4 0.2]
 [5.4 3.7 1.5 0.2]
 [5.9 3.2 4.8 1.8]
 [6.2 2.9 4.3 1.3]
 [4.9 3.  1.4 0.2]
 [5.2 4.1 1.5 0.1]
 [5.8 2.7 3.9 1.2]
 [6.4 3.2 4.5 1.5]
 [6.6 2.9 4.6 1.3]
 [7.  3.2 4.7 1.4]
 [6.9 3.1 4.9 1.5]
 [4.9 3.1 1.5 0.1]
 [6.5 3.  5.2 2. ]
 [4.8 3.  1.4 0.3]
 [6.3 3.3 4.7 1.6]
 [6.2 2.2 4.5 1.5]
 [6.7 3.  5.  1.7]
 [5.6 2.5 3.9 1.1]
 [5.9 3.  4.2 1.5]
 [6.  3.  4.8 1.8]
 [6.3 2.7 4.9 1.8]
 [5.3 3.7 1.5 0.2]
 [4.4 2.9 1.4 0.2]
 [6.4 2.7 5.3 1.9]
 [6.3 2.3 4.4 1.3]
 [6.2 2.8 4.8 1.8]
 [5.8 2.6 4.  1.2]
 [5.  3.  1.6 0.2]
 [5.9 3.  5.1 1.8]
 [5.8 4.  1.2 0.2]
 [5.6 2.8 4.9 2. ]
 [4.9 3.1 1.5 0.1]
 [4.6 3.2 1.4 0.2]
 [6.7 3.3 5.7 2.1]
 [6.4 2.8 5.6 2.2]
 [5.2 3.5 1.5 0.2]
 [6.5 2.8 4.6 1.5]
 [5.  3.2 1.2 0.2]
 [5.1 3.4 1.5 0.2]
 [5.4 3.9 1.3 0.4]
 [5.2 2.7 3.9 1.4]
 [4.9 3.1 1.5 0.1]
 [5.7 3.  4.2 1.2]
 [6.3 3.4 5.6 2.4]
 [6.1 2.8 4.7 1.2]
 [5.8 2.7 5.1 1.9]
 [4.6 3.4 1.4 0.3]
 [6.8 3.2 5.9 2.3]
 [6.  3.4 4.5 1.6]
 [4.7 3.2 1.3 0.2]
 [6.  2.9 4.5 1.5]
 [5.5 2.6 4.4 1.2]
 [6.2 3.4 5.4 2.3]
 [5.5 4.2 1.4 0.2]
 [6.3 2.8 5.1 1.5]
 [5.6 2.7 4.2 1.3]]
特征数据值of测试集 eigenValuesOfTestDataFrame：
 [[7.2 3.6 6.1 2.5]
 [6.1 2.8 4.  1.3]
 [5.  2.  3.5 1. ]
 [5.1 3.8 1.5 0.3]
 [4.8 3.4 1.9 0.2]
 [7.1 3.  5.9 2.1]
 [5.7 2.5 5.  2. ]
 [6.5 3.  5.8 2.2]
 [7.7 3.  6.1 2.3]
 [5.  3.4 1.5 0.2]
 [5.8 2.7 4.1 1. ]
 [6.8 3.  5.5 2.1]
 [6.3 2.9 5.6 1.8]
 [5.2 3.4 1.4 0.2]
 [5.8 2.7 5.1 1.9]
 [5.7 2.8 4.5 1.3]
 [5.7 3.8 1.7 0.3]
 [6.4 2.8 5.6 2.1]
 [6.7 3.  5.2 2.3]
 [5.5 2.4 3.8 1.1]
 [5.1 3.8 1.9 0.4]
 [6.6 3.  4.4 1.4]
 [6.9 3.1 5.1 2.3]
 [4.9 2.4 3.3 1. ]
 [5.8 2.8 5.1 2.4]
 [5.4 3.9 1.7 0.4]
 [4.6 3.1 1.5 0.2]
 [6.3 2.5 5.  1.9]
 [6.7 3.1 4.7 1.5]
 [7.7 3.8 6.7 2.2]
 [4.8 3.  1.4 0.1]
 [5.7 2.6 3.5 1. ]
 [5.1 3.5 1.4 0.2]
 [6.  2.2 5.  1.5]
 [4.4 3.2 1.3 0.2]
 [5.7 2.8 4.1 1.3]
 [5.1 3.5 1.4 0.3]
 [6.7 3.1 4.4 1.4]]
目标值of训练集 targetValuesOfTrainSeries：
 [0 1 2 2 2 1 1 1 0 1 0 0 1 0 2 1 0 1 0 2 2 2 0 0 2 2 0 2 2 1 2 1 0 2 0 2 1
 0 2 1 0 2 2 2 0 1 1 0 1 0 2 1 0 2 1 2 0 0 1 1 0 0 1 1 1 1 1 0 2 0 1 1 1 1
 1 2 2 0 0 2 1 2 1 0 2 0 2 0 0 2 2 0 1 0 0 0 1 0 1 2 1 2 0 2 1 0 1 1 2 0 2
 1]
目标值of测试集 targetValuesOfTestSeries：
 [2 1 1 0 0 2 2 2 2 0 1 2 2 0 2 1 0 2 2 1 0 1 2 1 2 0 0 2 1 2 0 1 0 2 0 1 0 1]

二、特征抽取 (使用scikit-learn进行数据的特征抽取)

1、字典类型数据----特征抽取

使用类：sklearn.feature_extraction.DictVectorizer

sklearn.feature_extraction.DictVectorizer的作用：对字典数据进行特征值化。即：把字典里的一些非数值型的数据分别转换为特征，然后用特征值(0或1)来表示该特征是否存在。待输入的数据要求为字典类型，如果原始数据不是字典类型，而是数组形式，需要将有类别的这些特征先要转换为字典数据，如果某些特征用不到，则不用提取(比如下图中的name，如果用不到，就不用提取出来)。

DictVectorizer语法：

DictVectorizer(sparse=True,…)，实例化
DictVectorizer.fit_transform(X) ，X:字典或者包含字典的迭代器；返回值：返回sparse矩阵
DictVectorizer.inverse_transform(X)，X:array数组或者sparse矩阵；返回值:转换之前数据格式
DictVectorizer.get_feature_names()，返回类别名称
DictVectorizer.transform(X)，按照原先的标准转换

字典特征抽取流程：

实例化类DictVectorizer
调用fit_transform方法输入数据并转换 (注意返回格式)

[{
     'city': '北京','temperature':100}
{
     'city': '上海','temperature':60}
{
     'city': '深圳','temperature':30}]

# 字典特征抽取
from sklearn.feature_extraction import DictVectorizer

def dictvec():
    """字典数据抽取"""
    # 实例化
    my_dict00 = DictVectorizer()  # 默认值为sparse=True，返回sparse矩阵
    # 调用fit_transform对字典格式的原始数据进行转换，默认返回sparse矩阵
    my_data00 = my_dict00.fit_transform([{
     'city': '北京', 'temperature': 100}, {
     'city': '上海', 'temperature': 60}, {
     'city': '深圳', 'temperature': 30}])
    print('转换后的特征值(sparse矩阵类型)：my_data00=\n', my_data00)
    my_dict = DictVectorizer(sparse=False)  # sparse=False 返回矩阵
    # 调用fit_transform对字典格式的原始数据进行转换，通过DictVectorizer(sparse=False)设置返回类型为矩阵(ndarray类型)，而不是默认的sparse矩阵
    my_data01 = my_dict.fit_transform([{
     'city': '北京', 'temperature': 100}, {
     'city': '上海', 'temperature': 60}, {
     'city': '深圳', 'temperature': 30}])
    # 获取类别名称
    feature_names = my_dict.get_feature_names()
    # 调用inverse_transform，返回转换之前数据格式
    my_data02 = my_dict.inverse_transform(my_data01)
    print('特征值列名：feature_names = my_dict.get_feature_names()=\n', feature_names)
    print('转换后的特征值(ndarray矩阵类型)：my_data01=\n', my_data01)
    print('my_data01.shape=', my_data01.shape)
    print('my_data02 = my_dict.inverse_transform(my_data01)=\n', my_data02)
    return None


if __name__ == "__main__":
    dictvec()

打印结果：

转换后的特征值(sparse矩阵类型)：my_data00=
   (0, 1)	1.0
  (0, 3)	100.0
  (1, 0)	1.0
  (1, 3)	60.0
  (2, 2)	1.0
  (2, 3)	30.0
特征值列名：feature_names = my_dict.get_feature_names()=
 ['city=上海', 'city=北京', 'city=深圳', 'temperature']
转换后的特征值(ndarray矩阵类型)：my_data01=
 [[  0.   1.   0. 100.]
 [  1.   0.   0.  60.]
 [  0.   0.   1.  30.]]
my_data01.shape= (3, 4)
my_data02 = my_dict.inverse_transform(my_data01)=
 [{
     'city=北京': 1.0, 'temperature': 100.0}, {
     'city=上海': 1.0, 'temperature': 60.0}, {
     'city=深圳': 1.0, 'temperature': 30.0}]

2、文本类型数据----特征抽取

2.1 方式一(抽取词频)：sklearn.feature_extraction.text.CountVectorizer

sklearn.feature_extraction.text.CountVectorizer的作用：对文本数据进行特征值化。首先将所有文章里的所有的词统计出来，重复的只统计一次。然后对每篇文章，在词的列表里面进行统计每个词出现的次数。注意：单个字母不统计(因为单个单词没有单词分类依据)。

DictVectorizer语法：

CountVectorizer(max_df=1.0,min_df=1,…)----实例化，返回词频矩阵
CountVectorizer.fit_transform(X,y)----X:文本或者包含文本字符串的可迭代对象；返回值：返回sparse矩阵
CountVectorizer.inverse_transform(X)----X:array数组或者sparse矩阵；返回值:转换之前数据格式
CountVectorizer.get_feature_names()----返回值:单词列表

文本特征抽取流程：

实例化类CountVectorizer
调用fit_transform方法输入数据并转换(注意返回格式，利用toarray()进行sparse矩阵转换array数组)
中文需要先进行分词，然后再进行特征抽取。

2.1.1 不带有中文的文本特征抽取

["life is short,i like python","life is too long,i dislike python"]

# 文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer

def countvec():
    """对文本进行特征值化"""
    cv = CountVectorizer()
    data = cv.fit_transform(["Python: life is short,i like python. it is python.", "life is too long,i dislike python. it is not python."])  # 列表里表示第一篇文章，第二篇文章
    print('cv.get_feature_names() = \n', cv.get_feature_names())
    print('data = \n', data)
    print('data.toarray() = \n', data.toarray())
    return None


if __name__ == "__main__":
    countvec()

打印结果：

cv.get_feature_names() = 
 ['dislike', 'is', 'it', 'life', 'like', 'long', 'not', 'python', 'short', 'too']
data = 
   (0, 2)	1
  (0, 4)	1
  (0, 8)	1
  (0, 1)	2
  (0, 3)	1
  (0, 7)	3
  (1, 6)	1
  (1, 0)	1
  (1, 5)	1
  (1, 9)	1
  (1, 2)	1
  (1, 1)	2
  (1, 3)	1
  (1, 7)	2
data.toarray() = 
 [[0 2 1 1 1 0 0 3 1 0]
 [1 2 1 1 0 1 1 2 0 1]]

2.1.2 带有中文的文本特征抽取(不进行分词)

有中文的文本特征抽取，如果不先进行中文分词，则将一段话当做一个词

["你们感觉人生苦短，你 喜欢python java javascript", "人生 漫长，我们 不喜欢python,react"]

# 文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer

def countvec():
    """对文本进行特征值化"""
    cv = CountVectorizer()
    data = cv.fit_transform(["你们感觉人生苦短，你 喜欢python java javascript", "人生 漫长，我们 不喜欢python,react"])  # 列表里表示第一篇文章，第二篇文章
    print('cv.get_feature_names() = \n', cv.get_feature_names())
    print('data = \n', data)
    print('data.toarray() = \n', data.toarray())
    return None


if __name__ == "__main__":
    countvec()

打印结果：

cv.get_feature_names() = 
 ['java', 'javascript', 'react', '不喜欢python', '人生', '你们感觉人生苦短', '喜欢python', '我们', '漫长']
data = 
   (0, 1)	1
  (0, 0)	1
  (0, 6)	1
  (0, 5)	1
  (1, 2)	1
  (1, 3)	1
  (1, 7)	1
  (1, 8)	1
  (1, 4)	1
data.toarray() = 
 [[1 1 0 0 0 1 1 0 0]
 [0 0 1 1 1 0 0 1 1]]

2.1.3 使用“jieba”库进行中文分词的文本特征抽取

安装：pip3 install jieba
使用：jieba.cut("我是一个好程序员")
返回值：词语生成器

# 文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer
import jieba

def cutword():
    """中文分词"""
    con1 = jieba.cut("今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。")
    con2 = jieba.cut("我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。")
    con3 = jieba.cut("如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。")
    # 转换成列表
    content1 = list(con1)
    content2 = list(con2)
    content3 = list(con3)
    # 把列表转换成字符串
    c1 = ' '.join(content1)
    c2 = ' '.join(content2)
    c3 = ' '.join(content3)
    return c1, c2, c3


def hanzivec():
    """中文特征值化"""
    c1, c2, c3 = cutword()
    print('c1 = \n', c1)
    print('c2 = \n', c2)
    print('c3 = \n', c3)
    cv = CountVectorizer()
    data = cv.fit_transform([c1, c2, c3])
    print('cv.get_feature_names() = \n', cv.get_feature_names())  # 单个词不统计
    print('data.toarray() = \n', data.toarray())

    return None


if __name__ == "__main__":
    hanzivec()

打印结果：

c1 = 
 今天 很 残酷 ， 明天 更 残酷 ， 后天 很 美好 ， 但 绝对 大部分 是 死 在 明天 晚上 ， 所以 每个 人 不要 放弃 今天 。
c2 = 
 我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 ， 这样 当 我们 看到 宇宙 时 ， 我们 是 在 看 它 的 过去 。
c3 = 
 如果 只用 一种 方式 了解 某样 事物 ， 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。
cv.get_feature_names() = 
 ['一种', '不会', '不要', '之前', '了解', '事物', '今天', '光是在', '几百万年', '发出', '取决于', '只用', '后天', '含义', '大部分', '如何', '如果', '宇宙', '我们', '所以', '放弃', '方式', '明天', '星系', '晚上', '某样', '残酷', '每个', '看到', '真正', '秘密', '绝对', '美好', '联系', '过去', '这样']
data.toarray() = 
 [[0 0 1 0 0 0 2 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 2 0 1 0 2 1 0 0 0 1 1 0 0 0]
 [0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 3 0 0 0 0 1 0 0 0 0 2 0 0 0 0 0 1 1]
 [1 1 0 0 4 3 0 0 0 0 1 1 0 1 0 1 1 0 1 0 0 1 0 0 0 1 0 0 0 2 1 0 0 1 0 0]]

2.2 方式二(tf-idf抽取词语的重要性)

API：sklearn.feature_extraction.text.TfidfVectorizer

tf：term frequency---->词频
idf：inverse document frequency---->逆文档频率=log( $\frac{总文档数量}{该词出现的文档数量}$ )
tf × idf---->该词在该篇文档中的重要性程度
tf-idf的主要思想是：如果某个词或短语在一篇文章中出现的概率高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。
tf-idf作用：用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
tf-idf是分类机器学习算法的重要依据。

tf-idf方法比count方法更好一些，但是在自然语言处理过程中会使用比tf-idf更好的方法【使用单字，使用n-garm，使用BM25，使用word2vec等，让其结果更加准确】。

2.2.1 tf-idf算法代码实现

import numpy as np
import pandas as pd
import math

### 1. 定义数据和预处理
docA = "The cat sat on my bed"
docB = "The dog sat on my knees"

bowA = docA.split(" ")
bowB = docB.split(" ")
print('bowA = {0}'.format(bowA))
print('bowB = {0}'.format(bowB))

# 构建词库
wordSet = set(bowA).union(set(bowB))
print('wordSet = {0}'.format(wordSet))

### 2. 进行词数统计
# 用统计字典来保存词出现的次数
wordDictA = dict.fromkeys(wordSet, 0)
wordDictB = dict.fromkeys(wordSet, 0)

# 遍历文档，统计词数
for word in bowA:
    wordDictA[word] += 1
for word in bowB:
    wordDictB[word] += 1

print('\nwordDataFrame = \n{0}'.format(pd.DataFrame([wordDictA, wordDictB])))


### 3. 计算词频tf=该词在文章A中的词频
def computeTF(wordDict, bow):
    # 用一个字典对象记录tf，把所有的词对应在bow文档里的tf都算出来
    tfDict = {
     }
    nbowCount = len(bow)
    for word, count in wordDict.items():
        tfDict[word] = count / nbowCount
    return tfDict


### 4. 计算逆文档频率idf=log(总文档数量/该词出现的文档数量)
def computeIDF(wordDictList):
    # 用一个字典对象保存idf结果，每个词作为key，初始值为0
    idfDict = dict.fromkeys(wordDictList[0], 0)
    N = len(wordDictList)
    for wordDict in wordDictList:
        # 遍历字典中的每个词汇，统计Ni
        for word, count in wordDict.items():
            if count > 0:
                # 先把Ni增加1，存入到idfDict
                idfDict[word] += 1
    # 已经得到所有词汇i对应的Ni，现在根据公式把它替换成为idf值
    for word, ni in idfDict.items():
        idfDict[word] = math.log10((N + 1) / (ni + 1))

    return idfDict


### 5. 计算TF-IDF
def computeTFIDF(tf, idfs):
    tfidf = {
     }
    for word, tfval in tf.items():
        tfidf[word] = tfval * idfs[word]
    return tfidf


if __name__ == '__main__':
    tfA = computeTF(wordDictA, bowA)
    tfB = computeTF(wordDictB, bowB)
    print('\ntfA = {0}'.format(tfA))
    print('tfB = {0}'.format(tfB))

    idfs = computeIDF([wordDictA, wordDictB])
    print('\nidfs = {0}'.format(idfs))

    tfidfA = computeTFIDF(tfA, idfs)
    tfidfB = computeTFIDF(tfB, idfs)
    print('\ntfidfDataFrame = \n{0}'.format(pd.DataFrame([tfidfA, tfidfB])))

打印结果：

bowA = ['The', 'cat', 'sat', 'on', 'my', 'bed']
bowB = ['The', 'dog', 'sat', 'on', 'my', 'knees']

wordSet = {
     'The', 'my', 'sat', 'knees', 'cat', 'on', 'bed', 'dog'}

wordDataFrame = 
   The  bed  cat  dog  knees  my  on  sat
0    1    1    1    0      0   1   1    1
1    1    0    0    1      1   1   1    1

tfA = {
     'The': 0.16666666666666666, 'my': 0.16666666666666666, 'sat': 0.16666666666666666, 'knees': 0.0, 'cat': 0.16666666666666666, 'on': 0.16666666666666666, 'bed': 0.16666666666666666, 'dog': 0.0}
tfB = {
     'The': 0.16666666666666666, 'my': 0.16666666666666666, 'sat': 0.16666666666666666, 'knees': 0.16666666666666666, 'cat': 0.0, 'on': 0.16666666666666666, 'bed': 0.0, 'dog': 0.16666666666666666}

idfs = {
     'The': 0.0, 'my': 0.0, 'sat': 0.0, 'knees': 0.17609125905568124, 'cat': 0.17609125905568124, 'on': 0.0, 'bed': 0.17609125905568124, 'dog': 0.17609125905568124}

tfidfDataFrame = 
   The       bed       cat       dog     knees   my   on  sat
0  0.0  0.029349  0.029349  0.000000  0.000000  0.0  0.0  0.0
1  0.0  0.000000  0.000000  0.029349  0.029349  0.0  0.0  0.0

2.2.2 tf-idf算法案例

# 文本特征抽取(tf-idf方式)
from sklearn.feature_extraction.text import TfidfVectorizer
import jieba

def cutword():
    """中文分词"""
    con1 = jieba.cut("今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。")
    con2 = jieba.cut("我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。")
    con3 = jieba.cut("如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。")
    # 转换成列表
    content1 = list(con1)
    content2 = list(con2)
    content3 = list(con3)
    # 把列表转换成字符串
    c1 = ' '.join(content1)
    c2 = ' '.join(content2)
    c3 = ' '.join(content3)
    return c1, c2, c3


def tfidfvec():
    """中文特征值化"""
    c1, c2, c3 = cutword()
    print('c1 = \n', c1)
    print('c2 = \n', c2)
    print('c3 = \n', c3)
    tfidf = TfidfVectorizer()
    data = tfidf.fit_transform([c1, c2, c3])
    print('tfidf.get_feature_names() = \n', tfidf.get_feature_names())
    print('data.toarray() = \n', data.toarray())

    return None


if __name__ == "__main__":
    tfidfvec()

打印结果：

c1 = 
 今天 很 残酷 ， 明天 更 残酷 ， 后天 很 美好 ， 但 绝对 大部分 是 死 在 明天 晚上 ， 所以 每个 人 不要 放弃 今天 。
c2 = 
 我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 ， 这样 当 我们 看到 宇宙 时 ， 我们 是 在 看 它 的 过去 。
c3 = 
 如果 只用 一种 方式 了解 某样 事物 ， 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。
tfidf.get_feature_names() = 
 ['一种', '不会', '不要', '之前', '了解', '事物', '今天', '光是在', '几百万年', '发出', '取决于', '只用', '后天', '含义', '大部分', '如何', '如果', '宇宙', '我们', '所以', '放弃', '方式', '明天', '星系', '晚上', '某样', '残酷', '每个', '看到', '真正', '秘密', '绝对', '美好', '联系', '过去', '这样']
data.toarray() = 
 [[0.         0.         0.21821789 0.         0.         0.
  0.43643578 0.         0.         0.         0.         0.
  0.21821789 0.         0.21821789 0.         0.         0.
  0.         0.21821789 0.21821789 0.         0.43643578 0.
  0.21821789 0.         0.43643578 0.21821789 0.         0.
  0.         0.21821789 0.21821789 0.         0.         0.        ]
 [0.         0.         0.         0.2410822  0.         0.
  0.         0.2410822  0.2410822  0.2410822  0.         0.
  0.         0.         0.         0.         0.         0.2410822
  0.55004769 0.         0.         0.         0.         0.2410822
  0.         0.         0.         0.         0.48216441 0.
  0.         0.         0.         0.         0.2410822  0.2410822 ]
 [0.15698297 0.15698297 0.         0.         0.62793188 0.47094891
  0.         0.         0.         0.         0.15698297 0.15698297
  0.         0.15698297 0.         0.15698297 0.15698297 0.
  0.1193896  0.         0.         0.15698297 0.         0.
  0.         0.15698297 0.         0.         0.         0.31396594
  0.15698297 0.         0.         0.15698297 0.         0.        ]]

三、特征的预处理(对数据进行处理)

特征的预处理：通过特定的统计方法（数学方法）将数据转换成算法要求的数据。
数值型数据预处理方法(缩放)：1、归一化；2、标准化；3、缺失值；并不是每个算法都需要缩放处理。
类别(String)型数据预处理方法：LabelEncode(Series)、OrdinalEncode(DataFrame)、OneHotEncode(one-hot编码可消除数值大小对算法的影响)；
时间型数据预处理方法：时间的切分；
scikit-learn所有的预处理方法都在sklearn. preprocessing类下

1、归一化方法(不常用)

1.1 归一化的目的

使得某一特征不会对最终结果造成比其他特征更大的影响。

1.2 特点

通过对原始数据进行变换把数据映射到(默认为[0,1])之间

注：作用于每一列，max为一列的最大值，min为一列的最小值,那么X’’为最终结果，mx，mi分别为指定区间值默认mx为1，mi为0。

1.3 sklearn归一化API: sklearn.preprocessing.MinMaxScaler

MinMaxScaler语法：

MinMaxScalar(feature_range=(0,1)…)，实例化，每个特征缩放到给定范围(默认[0,1])
MinMaxScalar.fit_transform(X)，X:numpy array格式的数据[n_samples,n_features]，返回值：转换后的形状相同的array

from sklearn.preprocessing import MinMaxScaler

def min_max():
    """归一化处理"""
    mm = MinMaxScaler()  # 默认：MinMaxScaler(feature_range=(0, 1))
    data = mm.fit_transform([[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]])
    print(data)
    return None


if __name__ == "__main__":
    min_max()

打印结果：

[[1.         0.         0.         0.        ]
 [0.         1.         1.         0.83333333]
 [0.5        0.5        0.6        1.        ]]

1.4 如果数据中异常点较多，会有什么影响？

注意在特定场景下最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，归一化方法只适合传统精确小数据场景。一般传统精确小数据场景不多，所以在实际应用中不太用归一化方法。

2、标准化方法(常用)

2.1 标准化的目的

使得某一特征不会对最终结果造成比其他特征更大的影响。

2.2 特点

通过对原始数据进行变换把数据变换到均值为0，方差为1 范围内。

2.3 sklearn标准化API: scikit-learn.preprocessing.StandardScaler

StandardScaler语法：

StandardScaler(…)，实例化，处理之后每列来说所有数据都聚集在均值0附近方差为1。
StandardScaler.fit_transform(X,y)，X:numpy array格式的数据[n_samples,n_features]，返回值：转换后的形状相同的array。
StandardScaler.mean_，原始数据中每列特征的平均值。
StandardScaler.std_，原始数据每列特征的方差。

from sklearn.preprocessing import StandardScaler

def stand():
    """标准化缩放"""
    std = StandardScaler()
    data = std.fit_transform([[1., -1., 3.], [2., 4., 2.], [4., 6., -1.]])
    print('data = \n', data)
    return None

if __name__ == "__main__":
    stand()

打印结果：

data = 
 [[-1.06904497 -1.35873244  0.98058068]
 [-0.26726124  0.33968311  0.39223227]
 [ 1.33630621  1.01904933 -1.37281295]]

2.4 标准化方法 V.S. 归一化方法

归一化：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变。
标准化：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小。在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

3、数值型数据离散化

4、时间型特征数据处理

5、统计型特征数据处理

6、缺失值的处理方法

注意：虽然scikit-learn也提供了缺失值的处理api，但是缺失值一般使用pandas来处理

6.1 缺失值的处理方法

删除----如果每列或者行数据缺失值达到一定的比例，建议放弃整行或者整列
插补(常用)----可以通过缺失值每行或者每列(比按行填补靠谱)的平均值、中位数来填充

6.2 sklearn缺失值API: sklearn.preprocessing.Imputer

Imputer语法：

Imputer(missing_values=‘NaN’, strategy=‘mean’, axis=0)，完成缺失值插补
Imputer.fit_transform(X,y) ，X:numpy array格式的数据[n_samples,n_features]，返回值：转换后的形状相同的array

Imputer流程：

初始化Imputer,指定”缺失值”，指定填补策略，指定行或列(缺失值也可以是别的指定要替换的值)；
调用fit_transform方法输入数据并转换；

from sklearn.preprocessing import Imputer
import numpy as np

def im():
    """缺失值处理"""
    # NaN, nan 两种写法都可以
    im = Imputer(missing_values='NaN', strategy='mean', axis=0)	# axis=0 表示按列求平均值
    data = im.fit_transform([[1, 2], [np.nan, 3], [7, 6]])
    print('data = \n', data)
    return None

if __name__ == "__main__":
    im()

打印结果：

data = 
 [[1. 2.]
 [4. 3.]
 [7. 6.]]

4.3 关于np.nan(np.NaN)

numpy的数组中可以使用np.nan/np.NaN来代替缺失值，属于float类型
如果是文件中的一些缺失值，可以替换成nan，通过np.array转化成float型的数组即可

四、数据降维(维度：特征的数量)

数据降维不是指数据矩阵的维度，而是指特征数量的减少。
数据降维方法：特征选择、主成分分析。

1、数据降维方式一：特征选择

特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征，特征在选择前和选择后可以改变值、也不改变值，但是选择后的特征维数肯定比选择前小，毕竟我们只选择了其中的一部分特征。
特征选择原因----冗余：部分特征的相关度高，容易消耗计算性能；噪声：部分特征对预测结果有负影响

特征选择主要方法（三大武器）：

Filter(过滤式)：VarianceThreshold
Embedded(嵌入式)：正则化、决策树
神经网络
Wrapper(包裹式)：基本用不到

1.1 Filter(过滤式)：VarianceThreshold

原则：把特征值差不多的特征删除掉，该特征对预测的作用不大。
用到的类：sklearn.feature_selection.VarianceThreshold，利用方差(Variance)进行过滤。
VarianceThreshold语法：

VarianceThreshold(threshold = 0.0)，删除所有低方差特征
Variance.fit_transform(X,y)，X:numpy array格式的数据[n_samples,n_features]，返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

VarianceThreshold流程

初始化VarianceThreshold,指定阀值方差。阀值方差根据实际情况来选择。阀值方差可以选0~9范围内的所有数，没有一个最好值，得根据实际效果来选择。
调用fit_transform

from sklearn.feature_selection import VarianceThreshold

def var():
    """特征选择-删除低方差的特征"""
    var = VarianceThreshold()   # 默认：threshold=0.0
    data = var.fit_transform([[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]])
    print('data = \n', data)
    return None

if __name__ == "__main__":
    var()

打印结果：

data = 
 [[2 0]
 [1 4]
 [1 1]]

1.2 Embedded(嵌入式)：正则化、决策树

1.3 神经网络

2、数据降维方式二：主成分分析(PCA)

主成分分析（Principal Component Analysis，PCA）：是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上用来降维的一种方法。

本质：PCA是一种分析、简化数据集的技术(当特征数量达到上百的时候，考虑数据的简化)。
目的：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。在降低维度时，尽可能减少损失。
作用：可以削减回归分析或者聚类分析中特征的数量。
用到的类：sklearn.decomposition

高维度数据容易出现的问题：特征之间通常是线性相关的或近似线性相关。

2.1 PCA理论基础：正交变换

正交向量：指点乘积(数量积)为零的两个或多个向量，若向量 $\vec{α}$ 与 $\vec{β}$ 正交，则 $\vec{α}$ · $\vec{β}$ =0，记为 $\vec{α}$ ⊥ $\vec{β}$ 。

正交矩阵(orthogonal matrix)：是一个方块矩阵(方阵)，其元素为实数，而且行(列)向量两两正交且是单位向量，使得该矩阵的转置矩阵为其逆矩阵： $Q^T$ = Q⁻¹ ⇔ $Q^T$ Q = Q $Q^T$ = E。
正交矩阵的行列式值必定为 + 1或 − 1。
作为一个线性映射（变换矩阵），正交矩阵保持距离不变，所以它是一个保距映射，具体例子为旋转与镜射。
行列式值为+1的正交矩阵，称为特殊正交矩阵，它是一个旋转矩阵。
行列式值为-1的正交矩阵，称为瑕旋转矩阵。瑕旋转是旋转加上镜射。镜射也是一种瑕旋转。

正交变换：是线性变换的一种，它从实内积空间V映射到V自身，且保证变换前后内积不变。因为向量的模长与向量间的夹角都是用内积定义的，所以正交变换前后一对向量各自的模长和它们的夹角都不变。

正交变换： Y’ = P * X = $\left[ \begin{matrix} {1\over \sqrt{2}} & -{1\over \sqrt{2}} \\ {1\over \sqrt{2}} & {1\over \sqrt{2}} \end{matrix} \right]$ * $\left[ \begin{matrix} -1 & -1 & 0 & 2 & 0\\ -2 & 0 & 0 & 1 & 1 \end{matrix} \right]$ = $\left[ \begin{matrix} {1\over \sqrt{2}} & -{1\over \sqrt{2}} & 0 & {1\over \sqrt{2}} & -{1\over \sqrt{2}} \\ -{3\over \sqrt{2}} & -{1\over \sqrt{2}} & 0 & {3\over \sqrt{2}} & {1\over \sqrt{2}} \end{matrix} \right]$

旋转矩阵(Rotation matrix)：是在乘以一个向量的时候有改变向量的方向但不改变大小的效果并保持了手性的矩阵。

通过旋转矩阵（属于正交矩阵，满足正交矩阵的一切性质）将原矩阵旋转到各个点的x分量(x₁, x₂, x₃, x₄ …)之间，或者y分量(y₁, y₂, y₃, y₄ …)之间，或者z分量(z₁, z₂, z₃, z₄ …)之间尽可能不相等。

二维旋转矩阵： $P$ = $\left[ \begin{matrix} sinθ & -sinθ \\ cosθ & cosθ \end{matrix} \right]$ $\overset{\text{θ=45°}}{===}$ $\left[ \begin{matrix} {1\over \sqrt{2}} & -{1\over \sqrt{2}} \\ {1\over \sqrt{2}} & {1\over \sqrt{2}} \end{matrix} \right]$

三维旋转矩阵： $P_x$ = $\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & cosθ_x & -sinθ_x \\ 0 & sinθ_x & cosθ_x \end{matrix} \right]$ ； $P_y$ = $\left[ \begin{matrix} cosθ_y & 0 & sinθ_y \\ 0 & 1 &0 \\ -sinθ_y & 0 & cosθ_y \end{matrix} \right]$ ； $P_z$ = $\left[ \begin{matrix} cosθ_z & -sinθ_z & 0 \\ sinθ_z & cosθ_z &0 \\ 0& 0 & 1\end{matrix} \right]$

Y’矩阵的第2行数据(y数据)各不相同，可以用来做降维处理。选取旋转矩阵P的第二行作为变换矩阵，左乘矩阵X得到一个线性变换后的行矩阵(行向量)。由原来的特征x、特征y(2个)减少为特征y(1个)，而且该保留下来的特征y包含了原数据的大部分信息。

Y’ = P * X = $\left[ \begin{matrix} {1\over \sqrt{2}} & {1\over \sqrt{2}} \end{matrix} \right]$ * $\left[ \begin{matrix} -1 & -1 & 0 & 2 & 0\\ -2 & 0 & 0 & 1 & 1 \end{matrix} \right]$ = $\left[ \begin{matrix} -{3\over \sqrt{2}} & -{1\over \sqrt{2}} & 0 & {3\over \sqrt{2}} & {1\over \sqrt{2}} \end{matrix} \right]$

PCA有两种通俗易懂的解释：(1)最大方差理论；(2)最小化降维造成的损失。这两个思路都能推导出同样的结果。

最大方差理论：最好的 $k$ 维特征是将 $n$ 维样本点转换为 $k$ 维后，每一个维度上的样本方差都很大，数据更加发散。将这些更加发散的数据提供给算法进行训练时，更有利于得出更好的模型。

样本 $\textbf{X}_{m×n}$ （其中 $m$ 为样品数量， $n$ 为特征数量）在 $\textbf{u}_{n×1}$ 向量方向上的投影为 $\textbf{X}_{m×n}·\textbf{u}$ ，其方差 $var=(\textbf{X}_{m×n}·\textbf{u}-\textbf{E})^2=(\textbf{X}_{m×n}·\textbf{u}-\textbf{E})^T·(\textbf{X}_{m×n}·\textbf{u}-\textbf{E})$
令数据中心化，则 $\textbf{E}=\textbf{0}$
方差 $var=(\textbf{X}_{m×n}·\textbf{u})^T·(\textbf{X}_{m×n}·\textbf{u})=\textbf{u}^T(\textbf{X}^T\textbf{X})_{n×n}\textbf{u}$ ，此方差 $v a r$ 是关于 $\textbf{u}$ 的一个函数，问题转为：就 $v a r (u)$ 的极大值。
令 $\textbf{u}$ 是单位向量，则 $|\textbf{u}|=1\implies\textbf{u}^T·\textbf{u}=1$ ；
问题转为求在约束条件 $\textbf{u}^T·\textbf{u}=1$ 下，求 $var=\textbf{u}^T(\textbf{X}^T\textbf{X})_{n×n}\textbf{u}$ 的极大值；
构造朗格朗日函数： $J(\textbf{u}) = \textbf{u}^T(\textbf{X}^T\textbf{X})_{n×n}\textbf{u} + λ(1-\textbf{u}^T·\textbf{u})$ ；
求朗格朗日函数 $J(\textbf{u})$ 对 $\textbf{u}$ 的偏导，并令其为0，此时所求的 $\textbf{u}$ 即是约束条件 $\textbf{u}^T·\textbf{u}=1$ 下函数 $var=\textbf{u}^T(\textbf{X}^T\textbf{X})_{n×n}\textbf{u}$ 的极大值处的 $\textbf{u}$ ；
$\begin{aligned}\frac{\partial{J(\textbf{u})}}{\partial{\textbf{u}}}=\frac{\partial{[ \textbf{u}^T(\textbf{X}^T\textbf{X})_{n×n}\textbf{u} + λ(1-\textbf{u}^T·\textbf{u})]}}{\partial{\textbf{u}}}=2(\textbf{X}^T\textbf{X})_{n×n}\textbf{u}-2λ\textbf{u}=0\end{aligned}$ ；
$\textbf{∴}$ $\begin{aligned}[(\textbf{X}^T\textbf{X})_{n×n}]\textbf{u}=λ\textbf{u}\end{aligned}$ ；
$\textbf{∴}$ $\begin{aligned}\{[(\textbf{X}^T\textbf{X})_{n×n}]-λ\textbf{E}\}\textbf{u}=0\end{aligned}$
$\begin{aligned}\{[(\textbf{X}^T\textbf{X})_{n×n}]-λ\textbf{E}\}\textbf{u}=0\end{aligned}$ 是一个 $n$ 个未知数 $n$ 个方程的齐次线性方程组，(参考：《线性代数》同济大学第六版 $p_{120}$ )它有非零解的充分必要条件是系数行列式
$\begin{aligned}\left|[(\textbf{X}^T\textbf{X})_{n×n}]-λ\textbf{E}\right|=0\end{aligned}$
$\textbf{∴}$ 求解未知数为 $\textbf{u}$ 的方程 $\begin{aligned}[(\textbf{X}^T\textbf{X})_{n×n}]\textbf{u}=λ\textbf{u}\end{aligned}$ 的解，就是求方阵 $(\textbf{X}^T\textbf{X})_{n×n}$ 的特征值 $λ$ 以及各个特征值分别对应的特征向量 $\textbf{u}$ ，其中特征值 $λ$ 及其对应的特征向量 $\textbf{u}$ 的数量为 $n$ ；
由于方阵 $(\textbf{X}^T\textbf{X})_{n×n}$ 是一个对称矩阵，所以求得的不同的特征值 $λ$ 对应的特征向量 $\textbf{u}$ 之间两两正交(方向垂直)；
$\textbf{∴}$ PCA方法找方差 $v a r$ 最大时的方向向量 $\textbf{u}$ ，就是找第一主成分；PCA方法找方差 $v a r$ 第二大时的方向向量 $\textbf{u}$ ，就是找第二主成分；方阵 $(\textbf{X}^T\textbf{X})_{n×n}$ 特征向量的数量为 $n$ 个，求出的主成分的数量为 $n$ 个。
PCA主成分分析降维，就是从 $n$ 个相互垂直的方向向量 $\textbf{u}_{n×1}$ 中选取 $(n - k)$ 个方向向量 $\textbf{u}_{n×1}$ ，然后将 $\textbf{X}_{m×n}$ 通过 $\textbf{X}_{m×n}×\textbf{u}_{n×1}^i$ 投影到各个 $\textbf{u}_{n×1}^i$ 方向上，得到各个方向向量 $\textbf{u}_{n×1}^i$ (特征 $i$ )上的数据 $\textbf{X}_{m×1}^i$ ，或者通过将 $n$ 个相互垂直的方向向量 $\textbf{u}_{n×1}$ 通过加权平均得到 $(n - k)$ 个方向向量 $\textbf{u}_{n×1}^i$ (特征 $i$ )上的数据 $\textbf{X}_{m×1}^i$ 。

2.2 PCA语法

2.2.1 PCA(n_components=None)

实例化，将数据分解为较低维数空间。
n_components可以为0~1的小数或整数。
n_components取小数时，表示PCA主成分分析之后信息保留量的百分比。经验表明一般填写0.9~0.95之间的小数。
n_components取整数时，表示PCA主成分分析之后所保留的特征的数量。一般不用此参数。

2.2.2 PCA.fit_transform(X)

X:numpy array格式的数据[n_samples,n_features]，返回值：转换后指定维度的array

2.3 PCA降维案例

2.3.1 PCA降维案例01

from sklearn.decomposition import PCA

def pca():
    """主成分分析进行特征降维"""
    pca070 = PCA(n_components=0.70)
    data070 = pca070.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print('data070 = \n', data070)
    pca080 = PCA(n_components=0.80)
    data080 = pca080.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print('data080 = \n', data080)
    pca099 = PCA(n_components=0.99)
    data099 = pca099.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
    print('data099 = \n', data099)
    return None

if __name__ == "__main__":
    pca()

打印结果：

data070 = 
 [[ 1.28620952e-15]
 [ 5.74456265e+00]
 [-5.74456265e+00]]
data080 = 
 [[ 1.28620952e-15  3.82970843e+00]
 [ 5.74456265e+00 -1.91485422e+00]
 [-5.74456265e+00 -1.91485422e+00]]
data099 = 
 [[ 1.28620952e-15  3.82970843e+00]
 [ 5.74456265e+00 -1.91485422e+00]
 [-5.74456265e+00 -1.91485422e+00]]

结果表明：

当n_components=0.70时，由原来的4个特征，最后保留了1个特征；
当n_components=0.80 时，由原来的4个特征，最后保留了2个特征；保留了原始数据的近80%的信息量。
当n_components=0.99 时，由原来的4个特征，最后保留了2个特征；保留了原始数据的近99%的信息量。

3、降维方法“特征选择”与“主成分分析”的选择

如果特征数量特别多(比如上百个)，则选择主成分分析的方法来降维；

五、scikit-learn转换器与估计器

1、scikit-learn转换器：实现特征工程的Api

1.1 fit(X)

对输入的数据X进行各种属性(平均值、方差…)的计算，但不输出任何数据。

1.2 transformer(Y)

根据上一步fit(X)函数计算的各种属性值(平均值、方差…)来计算输入的数据Y的各种结果，并输出转换后的数据。所以transformer(Y)的输出结果直接依赖于最紧邻的上一步fit(X)中计算出来的各种属性值(平均值、方差…)。

1.3 fit-transformer() = fit() + transformer()

输入数据后立刻计算各种属性值(平均值、方差…)然后输出转换后的数据。

2、scikit-learn估计器：实现算法的Api

2.1 用于分类的估计器

sklearn.neighbors k-近邻算法
sklearn.naive_bayes 贝叶斯
sklearn.linear_model.LogisticRegression 逻辑回归

2.2 用于回归的估计器：

sklearn.linear_model.LinearRegression 线性回归
sklearn.linear_model.Ridge 岭回归

2.3 用于聚类的估计器：

你可能感兴趣的:(#,机器学习/ML,人工智能,机器学习,python,数据分析)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
swagger访问路径 igotyback swagger
Swagger2.x版本访问地址：http://{ip}:{port}/{context-path}/swagger-ui.html{ip}是你的服务器IP地址。{port}是你的应用服务端口，通常为8080。{context-path}是你的应用上下文路径，如果应用部署在根路径下，则为空。Swagger3.x版本对于Swagger3.x版本（也称为OpenAPI3）访问地址：http://{ip
html 中如何使用 uniapp 的部分方法某公司摸鱼前端 html uni-app 前端
示例代码：Documentconsole.log(window);效果展示：好了，现在就可以uni.使用相关的方法了
高级编程--XML+socket练习题 masa010 java 开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人（1）使用dom4j将信息存入xml中（2）读取信息，并打印控制台（3）添加一个city节点与子节点（4）使用socketTCP协议编写服务端与客户端，客户端输入城市ID，服务器响应相应城市信息（5）使用socketTCP协议编写服务端与客户端，客户端要求用户输入city对象，服务端接收并使用dom4j
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计网页设计期末网页作业 html静态网页 html5期末大作业网页设计 web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript 二挡起步 web前端期末大作业 javascript html css 旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业，Web大学生网页HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
HTML网页设计制作大作业（div+css）云南我的家乡旅游景点带文字滚动二挡起步 web前端期末大作业 web设计网页规划与设计 html css javascript dreamweaver 前端
Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript：做与用户的交互行为文章目录前端学习路线
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
【目标检测数据集】卡车数据集1073张VOC+YOLO格式熬夜写代码的平头哥∰ 目标检测 YOLO 人工智能
数据集格式：PascalVOC格式+YOLO格式(不包含分割路径的txt文件，仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数)：1073标注数量(xml文件个数)：1073标注数量(txt文件个数)：1073标注类别数：1标注类别名称:["truck"]每个类别标注的框数：truck框数=1120总框数：1120使用标注工具：labelImg标注
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
钢筋长度超限检测检数据集VOC+YOLO格式215张1类别 futureflsl 数据集 YOLO 深度学习机器学习
数据集格式：PascalVOC格式+YOLO格式(不包含分割路径的txt文件，仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数)：215标注数量(xml文件个数)：215标注数量(txt文件个数)：215标注类别数：1标注类别名称:["iron"]每个类别标注的框数：iron框数=215总框数：215使用标注工具：labelImg标注规则：对类别进
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
ztree设置禁用节点 3213213333332132 JavaScript ztree json setDisabledNode Ajax
ztree设置禁用节点的时候注意，当使用ajax后台请求数据,必须要设置为同步获取数据，否者会获取不到节点对象，导致设置禁用没有效果。 $(function(){ showTree(); setDisabledNode(); });
JVM patch by Taobao bookjovi java HotSpot
在网上无意中看到淘宝提交的hotspot patch，共四个，有意思，记录一下。 7050685：jsdbproc64.sh has a typo in the package name 7058036：FieldsAllocationStyle=2 does not work in 32-bit VM 7060619：C1 should respect inline and
将session存储到数据库中 dcj3sjt126com sql PHP session
CREATE TABLE sessions ( id CHAR(32) NOT NULL, data TEXT, last_accessed TIMESTAMP NOT NULL, PRIMARY KEY (id) ); <?php /** * Created by PhpStorm. * User: michaeldu * Date
Vector 171815164 vector
public Vector<CartProduct> delCart(Vector<CartProduct> cart, String id) { for (int i = 0; i < cart.size(); i++) { if (cart.get(i).getId().equals(id)) { cart.remove(i);
各连接池配置参数比较 g21121 连接池
排版真心费劲，大家凑合看下吧，见谅~ Druid DBCP C3P0 Proxool 数据库用户名称 Username Username User 数据库密码 Password Password Password 驱动名
[简单]mybatis insert语句添加动态字段 53873039oycg mybatis
mysql数据库,id自增,配置如下： <insert id="saveTestTb" useGeneratedKeys="true" keyProperty="id" parameterType=&
struts2拦截器配置云端月影 struts2拦截器
struts2拦截器interceptor的三种配置方法方法1. 普通配置法 <struts> <package name="struts2" extends="struts-default"> &
IE中页面不居中，火狐谷歌等正常 aijuans IE中页面不居中
问题是首页在火狐、谷歌、所有IE中正常显示，列表页的页面在火狐谷歌中正常，在IE6、7、8中都不中，觉得可能那个地方设置的让IE系列都不认识，仔细查看后发现，列表页中没写HTML模板部分没有添加DTD定义，就是<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3
String,int,Integer,char 几个类型常见转换 antonyup_2006 html sql .net
如何将字串 String 转换成整数 int? int i = Integer.valueOf(my_str).intValue(); int i=Integer.parseInt(str); 如何将字串 String 转换成Integer ? Integer integer=Integer.valueOf(str); 如何将整数 int 转换成字串 String ? 1.
PL/SQL的游标类型百合不是茶显示游标(静态游标)隐式游标游标的更新和删除 %rowtype ref游标(动态游标)
游标是oracle中的一个结果集,用于存放查询的结果; PL/SQL中游标的声明; 1,声明游标 2,打开游标(默认是关闭的); 3,提取数据 4,关闭游标注意的要点:游标必须声明在declare中,使用open打开游标,fetch取游标中的数据,close关闭游标隐式游标:主要是对DML数据的操作隐
JUnit4中@AfterClass @BeforeClass @after @before的区别对比 bijian1013 JUnit4 单元测试
一.基础知识 JUnit4使用Java5中的注解（annotation），以下是JUnit4常用的几个annotation： @Before：初始化方法对于每一个测试方法都要执行一次（注意与BeforeClass区别，后者是对于所有方法执行一次）@After：释放资源对于每一个测试方法都要执行一次（注意与AfterClass区别，后者是对于所有方法执行一次
精通Oracle10编程SQL(12)开发包 bijian1013 oracle 数据库 plsql
/* *开发包 *包用于逻辑组合相关的PL/SQL类型（例如TABLE类型和RECORD类型）、PL/SQL项（例如游标和游标变量）和PL/SQL子程序（例如过程和函数） */ --包用于逻辑组合相关的PL/SQL类型、项和子程序，它由包规范和包体两部分组成 --建立包规范：包规范实际是包与应用程序之间的接口，它用于定义包的公用组件，包括常量、变量、游标、过程和函数等 --在包规
【EhCache二】ehcache.xml配置详解 bit1129 ehcache.xml
在ehcache官网上找了多次，终于找到ehcache.xml配置元素和属性的含义说明文档了，这个文档包含在ehcache.xml的注释中！ ehcache.xml ： http://ehcache.org/ehcache.xml ehcache.xsd ： http://ehcache.org/ehcache.xsd ehcache配置文件的根元素是ehcahe ehcac
java.lang.ClassNotFoundException: org.springframework.web.context.ContextLoaderL 白糖_ java eclipse spring tomcat Web
今天学习spring+cxf的时候遇到一个问题：在web.xml中配置了spring的上下文监听器： <listener> <listener-class>org.springframework.web.context.ContextLoaderListener</listener-class> </listener> 随后启动
angular.element boyitech AngularJS AngularJS API angular.element
angular.element 描述: 包裹着一部分DOM element或者是HTML字符串，把它作为一个jQuery元素来处理。（类似于jQuery的选择器啦）如果jQuery被引入了，则angular.element就可以看作是jQuery选择器，选择的对象可以使用jQuery的函数；如果jQuery不可用，angular.e
java-给定两个已排序序列，找出共同的元素。 bylijinnan java
import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class CommonItemInTwoSortedArray { /** * 题目：给定两个已排序序列，找出共同的元素。 * 1.定义两个指针分别指向序列的开始。 * 如果指向的两个元素
sftp 异常，有遇到的吗？求解 Chen.H java jcraft auth jsch jschexception
com.jcraft.jsch.JSchException: Auth cancel at com.jcraft.jsch.Session.connect(Session.java:460) at com.jcraft.jsch.Session.connect(Session.java:154) at cn.vivame.util.ftp.SftpServerAccess.connec
[生物智能与人工智能]神经元中的电化学结构代表什么? comsci 人工智能
我这里做一个大胆的猜想,生物神经网络中的神经元中包含着一些化学和类似电路的结构,这些结构通常用来扮演类似我们在拓扑分析系统中的节点嵌入方程一样,使得我们的神经网络产生智能判断的能力,而这些嵌入到节点中的方程同时也扮演着"经验"的角色.... 我们可以尝试一下...在某些神经
通过LAC和CID获取经纬度信息 dai_lm lac cid
方法1：用浏览器打开http://www.minigps.net/cellsearch.html，然后输入lac和cid信息(mcc和mnc可以填0)，如果数据正确就可以获得相应的经纬度方法2：发送HTTP请求到http://www.open-electronics.org/celltrack/cell.php?hex=0&lac=<lac>&cid=&
JAVA的困难分析 datamachine java
前段时间转了一篇SQL的文章（http://datamachine.iteye.com/blog/1971896），文章不复杂，但思想深刻，就顺便思考了一下java的不足，当砖头丢出来，希望引点和田玉。 -----------------------------------------------------------------------------------------
小学5年级英语单词背诵第二课 dcj3sjt126com english word
money 钱 paper 纸 speak 讲，说 tell 告诉 remember 记得，想起 knock 敲，击，打 question 问题 number 数字，号码 learn 学会，学习 street 街道 carry 搬运，携带 send 发送，邮寄，发射 must 必须 light 灯，光线，轻的 front
linux下面没有tree命令 dcj3sjt126com linux
centos p安装 yum -y install tree mac os安装 brew install tree 首先来看tree的用法 tree 中文解释：tree 功能说明：以树状图列出目录的内容。语　　法：tree [-aACdDfFgilnNpqstux][-I <范本样式>][-P <范本样式
Map迭代方式，Map迭代，Map循环蕃薯耀 Map循环 Map迭代 Map迭代方式
Map迭代方式，Map迭代，Map循环 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年
Spring Cache注解+Redis hanqunfeng spring
Spring3.1 Cache注解依赖jar包：  <dependency> <groupId>org.springframework.data</groupId> <artifactId>spring-data-redis</artifactId>
Guava中针对集合的 filter和过滤功能 jackyrong filter
在guava库中，自带了过滤器(filter)的功能，可以用来对collection 进行过滤，先看例子： @Test public void whenFilterWithIterables_thenFiltered() { List<String> names = Lists.newArrayList("John"
学习编程那点事 lampcy 编程 android PHP html5
一年前的夏天，我还在纠结要不要改行，要不要去学php？能学到真本事吗？改行能成功吗？太多的问题，我终于不顾一切，下定决心，辞去了工作，来到传说中的帝都。老师给的乘车方式还算有效，很顺利的就到了学校，赶巧了，正好学校搬到了新校区。先安顿了下来，过了个轻松的周末，第一次到帝都，逛逛吧！接下来的周一，是我噩梦的开始，学习内容对我这个零基础的人来说，除了勉强完成老师布置的作业外，我已经没有时间和精力去
架构师之流处理---------bytebuffer的mark,limit和flip nannan408 ByteBuffer
1.前言。如题，limit其实就是可以读取的字节长度的意思，flip是清空的意思，mark是标记的意思。 2.例子. 例子代码: String str = "helloWorld"; ByteBuffer buff = ByteBuffer.wrap(str.getBytes()); Sy
org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1, column 1 Everyday都不同 $转义 el表达式
最近在做Highcharts的过程中，在写js时，出现了以下异常：严重: Servlet.service() for servlet jsp threw exception org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1,
用Java实现发送邮件到163 tntxia java实现
/* 在java版经常看到有人问如何用javamail发送邮件？如何接收邮件？如何访问多个文件夹等。问题零散，而历史的回复早已经淹没在问题的海洋之中。本人之前所做过一个java项目，其中包含有WebMail功能，当初为用java实现而对javamail摸索了一段时间，总算有点收获。看到论坛中的经常有此方面的问题，因此把我的一些经验帖出来，希望对大家有些帮助。此篇仅介绍用
探索实体类存在的真正意义 java小叶檀 POJO
一. 实体类简述实体类其实就是俗称的POJO,这种类一般不实现特殊框架下的接口，在程序中仅作为数据容器用来持久化存储数据用的 POJO（Plain Old Java Objects）简单的Java对象它的一般格式就是 public class A{ private String id; public Str