前言
wei,zaima?
摸了一个月还行【狗头】
不知道开头怎么写了,尬就完事了。
要看题解的请移步:传送门
正文
Why 并查集
首先来解释一下什么是 并 查 集 这三个字的意思:
- 并,俗称∪,就是把两个数据放到一个集合里面,
什么,你不懂集合?那你可以滚了。 - 查,就是查这个数据和其他的哪些数据在一个集合里面
如果写过万恶的树的同志们其实也就可以把查的过程理解为找当前叶子节点的根节点了,然后再统计有哪些叶子在一个根上,就可以判断这些所有的叶子都在一棵树上 - 集 顾名思义,就是集合的意思,
对于有一些题目,我们自己用STL中封装好的set就可以完成操作,但请记住,那只是一个集合,如果遇到需要很多很多的集合的,like this:
在社交的过程中,通过朋友,也能认识新的朋友。在某个朋友关系图中,假定 A 和 B 是朋友,B 和 C 是朋友,那么 A 和 C 也会成为朋友。即,我们规定朋友的朋友也是朋友。 现在,已知若干对朋友关系,询问某两个人是不是朋友。
这道题目棘手的地方就在于说你不确定说有几个set,对于这道题,我们就可以引入并查集的概念了,利用一棵树来维护N个set,
下面进入装逼时间【B站补习团:传送门】
视频基本思路和我一样会,但是实际操作我就很皮了,【算法竞赛宝典没有讲并查集,哭了】
1.首先并查集的精髓在于一个father[marx]数组,这个数组的储存的是每一个叶子的根节点,for example ,想要说1这个叶子的根是2,只需要让father[1]=2,非常简单是不是
2.那么怎么让多个树叶属于同一个集合内呢?很简单只需要让father[3]=2,这样3的根节点也是2了,那么1,2,3就属于同一个set内了。
首先我们先初始化father数组,使得每一个节点的根节点=它本身,这样每一个点都是一个单独的集合了:
#include
using namespace std;
const int maxn=1e+7;
int n,m,p;
int father[maxn],dist[maxn],size[maxn];//dist元素到根节点的距离 size集合中元素个数
void init(){
for(int i=1;i<=n;++i){
father[i]=i,dist[i]=0,size[i]=1;//因为初始化的时候,所有的节点本身就是根节点,所以dist也就为0了,总结点数为1.
}
}
接下来就是最重要的重头戏了,寻找梗节点,这就需要用到递归了:
int get(int x){//get父节点+当前节点和父节点之间的关系
if(father[x]==x){ //如果当前x的根节点就是x,则返回
return x;
}
int y=father[x];//让y=x的父节点
father[x]=get(y);//直接把当前x的父节点从y改成get(y),也就是y的父节点【x的爷爷节点】 --> 路径压缩
dist[x]+=dist[y];//x到根节点的距离加上x的父节点到根节点的
return father[x];//返回x的父节点
}
为什么说返回的是x的父节点,而不是根节点呢?
按照题面的说法是:你需要让X所在的队列的所有元素,作为一个整体(头在前尾在后)接至Y所在的队列的尾部
按照上面的操作下来,我们最后读取这个并查集的时候可能会超时,与其老老实实的把x接在y的后面,还不如把x接在y的根节点的后面,反正都是在同一个根上->同一个集合了。
最后就是 并 ,merge了,也非常的简单呢
void merge(int a,int b){
fa=get(a); //fa=a的根节点
fb=get(b);//fb=b的根节点
if(fa!=fb){//如果a的根节点≠b的根节点 -> a、b不在同一个集合中。
father[fa]=fb; //把a的根节点的根节点设置为b的根节点
dist[fa]=size[fb];//fa到根节点的距离自然就多了size[b]个
size[fb]+=size[fa];总节点数=a的总数+b的总数
}
}
下面就来结合上面那到题目运动一下?
运♂动
在社交的过程中,通过朋友,也能认识新的朋友。在某个朋友关系图中,假定 A 和 B 是朋友,B 和 C 是朋友,那么 A 和 C 也会成为朋友。即,我们规定朋友的朋友也是朋友。 现在,已知若干对朋友关系,询问某两个人是不是朋友。
输入格式
第一行:三个整数 n,m,p(n≤5000,m≤5000,p≤5000),分别表示有 n 个人,m 个朋友关系,询问 p 对朋友关系。
接下来 m 行:每行两个数Ai,Bi(0<=Ai,Bi<=N)表示 Ai和 Bi具有朋友关系。
接下来 p 行:每行两个数,询问两人是否为朋友。
输出格式
输出共 p 行,每行一个Yes或No。表示第 ii 个询问的答案为是否朋友。
样例输入
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
样例输出
Yes
Yes
No
AC代码
#include
using namespace std;
const int maxn=1e+7;
int n,m,p;
int father[maxn],dist[maxn],size[maxn];//dist元素到根节点的距离 size集合中元素个数
void init(){
for(int i=1;i<=n;++i){
father[i]=i,dist[i]=0,size[i]=1;
}
}
int get(int x){
if(father[x]==x){
return x;
}
int y=father[x];
father[x]=get(y);
dist[x]+=dist[y];
return father[x];
}
void merge(int a,int b){
a=get(a);
b=get(b);
if(a!=b){
father[a]=b;
dist[a]=size[b];
size[b]+=size[a];
}
}
string check(int a,int b)
{
if(get(a)==get(b))return "Yes";
else return "No";
}
int main()
{
cin>>n>>m>>p;
init();
for(int i=0;i>A>>B;
merge(A,B);
}
for(int i=0;i>A>>B;
/*if(get(A)==get(B))
{
cout<<"Yes"< 下面是正经题了,头脑风暴请注意......
题面
蒜头君有很多卡片,每张卡片正面上印着“剪刀”,“石头”或者“布”三种图案中的一种,反面则印着卡片的序号。“剪刀”,“石头”和“布”三种构成了一个有趣的环形,“剪刀”可以战胜“布”,“布”可以战胜“石头”,“石头”可以战胜“剪刀”。
现有 N 张卡片,以 1-N 编号。每张卡片印着“剪刀”,“石头”,“布”中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 张卡片所构成的关系进行描述:
- 第一种说法是“1 X Y”,表示 X 号卡片和 Y 号卡片是同一种卡片。
- 第二种说法是“2 X Y”,表示 X 号卡片可以战胜 Y 号卡片。
蒜头君对 N 张卡片,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 X 或 Y 的值比 N 大,就是假话;
- 当前的话表示 X 能战胜 X ,就是假话。
你的任务是根据给定的 N 和 K 句话,计算假话的总数。
输入格式
第一行是两个整数 N(1≤N≤50,000) 和 K(0≤K≤100,000),以一个空格分隔。
以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1,则表示 X 和 Y 是同一种卡片。
若 D=2,则表示 X 能战胜 Y。
输出格式
只有一个整数,表示假话的数目。
分析思路
我们现在需要一种数据结构来模拟这样一个条件:
- X与Y相等,X对Y的关系记为0,
- X可战胜Y,X对Y的关系记为1,
- X被Y战胜,X对Y的关系记为2,
无论当前卡牌是什么关系,都可以和另外一个张牌用如上三种关系来表达,
但是,最最最重要也是最最困难的是:
我i们需要利用其中两个关系来推到出第三个关系,举一个栗子:
X1与X2的图案相等,X1可以战胜Y,我们需要让程序推导出X2也可以战胜Y才行,
emmmmmmmmm........
推荐带权并查集吧,我虽然不知道每个卡片的图案,但是我知道卡片之间的关系。
那么可以把已知关系的点合并在一棵树上,然后记录每个点与根结点的关系。只要一直维护每个点与根结点的关系,这样我们就可以判断某一个描述是否与之前的描述冲突了。
上手撸
1.创建一个rns数组用来记录每一个节点与根节点的关系,
- 0表示与根节点相同,
- 1表示被根节点战胜,
- 2表示战胜根节点,
可以发现A到B和B到C的rns关系加起来%3就是A到C的关系,也就是这里算rnk的原理。
假设A,B,C分别为石头,石头和剪刀,下面纯数论来模拟一下,
A --0-> B 【表示A和B相同】
B --1-> C 【表示B可以战胜C】 推导出 【A也可以战胜C】
A --(0+1)%3=1-> 【rns运算出A可以战胜C】
并查集中的get方法就是用到了上面的数论关系:
int get(int x) //get父节点+当前节点和父节点之间的关系
{
if(father[x]==x)return x; //如果当前x的根节点就是x,则返回
else
{
int y=father[x]; //让y=x的父节点
father[x]=get(father[x]);//直接把当前x的父节点从y改成get(y),也就是y的父节点 --> 路径压缩
rns[x]=(rns[x]+rns[y])%3; //之前x的父节点与之前的x的父节点的父节点【爷爷节点?】的关系
return father[x]; //返回x的父节点
}
}
这段里面加了一个计算rns爷爷节点关系的语句【大雾】,手动走一遍应该就知道了,
为什么我们要计算rns爷爷节点呢?因为上面我们把通过y这个媒介把x的父节点变成了x的爷爷节点。这就是所谓的路径压缩,
因为rns记录的其实是x与father[x]的关系
2.我们先创建一个并查集,写上init,get和merge:
void init() //初始化
{
for(int i=1;i<=n;++i)
{
father[i]=i;
}
}
int get(int x) //get父节点+当前节点和父节点之间的关系
{
if(father[x]==x)return x; //如果当前x的根节点就是x,则返回
else
{
int y=father[x]; //让y=x的父节点
father[x]=get(father[x]);//直接把当前x的父节点从y改成get(y),也就是y的父节点 --> 路径压缩
rns[x]=(rns[x]+rns[y])%3; //之前x的父节点与之前的x的父节点的父节点【爷爷节点?】的关系
return father[x]; //返回x的父节点
}
}
void merge(int x,int y,int d)
{
int fx,fy;
fx=get(x); //获取x的根节点
fy=get(y); //获取y的根节点
if(fx!=fy) //如果x的根没有等于y的根,持续操作直至相等,因为根相等,故在同一个set内,合并完成
{
father[fx]=fy; // 把fx的父节点变成fy,下一次循环就是把y的父节点变成y的爷爷节点,直到找到y的根儿为止
rns[fx]=(rns[y]-rns[x]+d+3)%3;
/*
这里求的是fx【x的根节点】的与fy之间的关系,因为要合并两个根节点嘛
假设x可以战胜y,则关系记为1,
那么y被x战胜,关系即位2,
现在输入1XY,D=1表示X战胜Y,
那么x的根节点fx推到出来的关系应该是:(1-2+1+3)%3=1,那么fx也可以战胜y
*/
}
else if((rns[x]-rns[y]+3)%3!=d) //当fx=fy【合并完成?】的时候,如果 x对y的关系 和 y对x的关系 推到出来的结果不是D的话,则为谎言
{
ans++;
}
return;
}
reltion就是我们所谓的权了,也就是rns。
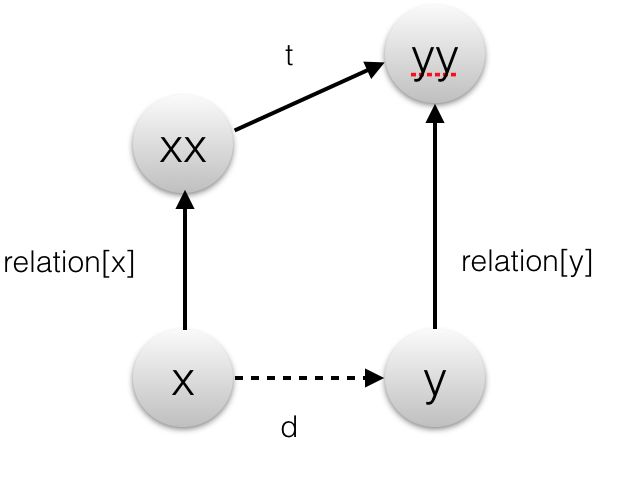
(reltion[x] + t)%3 =(d+relation[y])%3, 假设x是布,x的根节点xx是石头,那么x就可以战胜xx,relation[x]记为1, 假设y为石头,y的根节点yy是布,那么yy就可以战胜y,relation[y]记为2. 由上可知x可以战胜y,那么推导得出d为1,所以t=(d + relation[y] - relation[x] + 3) %3 t=(1+2-1+3)%3=2,得到xx被yy战胜。
Q.E.D !【imn特有的论证方法!(确信)】
所以我们只需要每一次计算当前x的根节点和y的根节点的关系,直到x的根节点=y的根节点的时候,再检验fx与fy的关系时候和x,y计算出来的一样就行了。
【很简单的,我也只不过卡了一周而已】
AC部警告
#include
using namespace std;
const int maxn=50001;
int n,K,ans,father[maxn],rns[maxn];
/*
0表示与根节点相同,
1表示被根节点战胜,
2表示战胜根节点,
可以发现a到b和b到c的关系加起来模3就是a到c的关系,也就是这里算rnk的原理。
A --0-> B 【表示A和B相同】
B --1-> C 【表示B可以战胜C】 推导出 【A也可以战胜C】
A --(0+1)%3=1-> 【rns运算出A可以战胜C】
*/
void init() //初始化
{
for(int i=1;i<=n;++i)
{
father[i]=i;
}
}
int get(int x) //get父节点+当前节点和父节点之间的关系
{
if(father[x]==x)return x; //如果当前x的根节点就是x,则返回
else
{
int y=father[x]; //让y=x的父节点
father[x]=get(father[x]);//直接把当前x的父节点从y改成get(y),也就是y的父节点 --> 路径压缩
rns[x]=(rns[x]+rns[y])%3; //之前x的父节点与之前的x的父节点的父节点【爷爷节点?】的关系
return father[x]; //返回x的父节点
}
}
void merge(int x,int y,int d)
{
int fx,fy;
fx=get(x); //获取x的根节点
fy=get(y); //获取y的根节点
if(fx!=fy) //如果x的根没有等于y的根,持续操作直至相等,因为根相等,故在同一个set内,合并完成
{
father[fx]=fy; // 把x的父节点变成y,下一次循环就是把y的父节点变成y的爷爷节点,直到找到y的根儿为止
rns[fx]=(rns[y]-rns[x]+d+3)%3;
/*
这里求的是fx【x的*根*节点】的与fy之间的关系,因为要合并两个根节点嘛
假设x可以战胜y,则关系记为1,
那么y被x战胜,关系即位2,
现在输入1XY,D=1表示X战胜Y,
那么x的根节点fx推到出来的关系应该是:(1-2+1+3)%3=1,那么fx也可以战胜y
*/
}
else if((rns[x]-rns[y]+3)%3!=d) //当fx=fy【合并完成?】的时候,如果 x对y的关系 和 y对x的关系 推到出来的结果不是D的话,则为谎言
{
ans++;
}
return;
}
int main()
{
cin>>n>>K;
init();//这个一定要放在输入n后面,不然就没有初始化
for(int i=0;i>D>>X>>Y;
if(X>n||Y>n||(D==2&&X==Y))
{
ans++;
//continue;
}
else
{
merge(X,Y,D-1);
}
}
cout< 瞎扯几句
我画不出来还行。
参考资料:
练习题:找出所有谎言
B站真是太棒了⑧
必须参考的资料:
这不是一个技术向blog