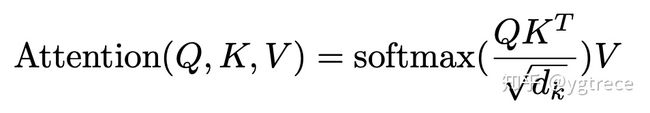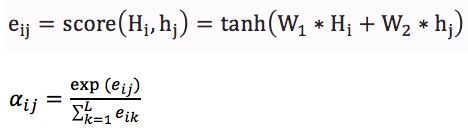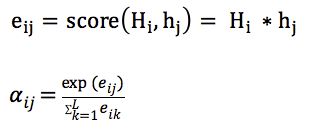HAH-M

阅读笔记--NLP面试基础知识总结

如果我可以把今世的记忆带到以后，我会告诉我下一世的继任者去学数学。但是他可能又是一个不愿意学习的小傻瓜，或许三年级的时候还是会考各种0分。是呀，0分也是回忆，那时怎么会晓得走到现在，今后又晓得会去往何处。但是…，谁又会到全局最优解呢？我在这里，我不知道人生接下来会给我怎样的惊吓和惊喜，我现在处在的地方可能就是局部最优解吧！

一、深度学习和机器学习的区别

数据相关性: 深度学习与传统机器学习最重要的区别是，随着数据量的增加，其性能也随之提高。当数据很小的时候，深度学习算法并不能很好地执行，这是因为深度学习算法需要大量的数据才能完全理解它。
硬件支持：深度学习需要强有力的GPU或者TPU支持
特征工程：在机器学习中，大多数应用的特征需要由专家识别，然后根据域和数据类型手工编码。但是深度学习一般是自动抽取特征
执行时间：深度学习模型的执行时间很长，但是机器学习一般较短
可解释性：深度学习的可解释性比较差。

二、基本概念

什么是分词(Tokenization)？

分词

什么是序列标注？

NLP之序列标注问题

所谓的序列标注就是对输入的文本序列中的每个元素打上标签集合中的标签。例如输入的一个序列如下：
$X = {x_{1}, x_{2}, ..., x_{n}}$
那么经过序列标注后每个元素对应的标签如下：
$Y = {y_{1}, y_{2}, ..., y_{n}}$
所以，其本质上是对线性序列中每个元素根据上下文内容进行分类的问题。一般情况下，对于NLP任务来说，线性序列就是输入的文本，往往可以把一个汉字看做线性序列的一个元素，而不同任务其标签集合代表的含义可能不太相同，但是相同的问题都是：如何根据汉字的上下文给汉字打上一个合适的标签（无论是分词，还是词性标注，或者是命名实体识别，道理都是想通的）

什么是end-to-end

三、表示学习

1.nlp中的词向量对比：word2vec/glove/fastText/elmo/GPT/bert

词向量是自然语言处理任务中非常重要的一个部分，词向量的表征能力很大程度上影响了自然语言处理模型的效果。如论文中所述，词向量需要解决两个问题：
(1). 词使用的复杂特性，如句法和语法。
(2). 如何在具体的语境下使用词，比如多义词的问题。

传统的词向量比如word2vec能够解决第一类问题，但是无法解决第二类问题。比如：“12号地铁线马上就要开通了，以后我们出行就更加方便了。”和“你什么时候方便，我们一起吃个饭。”这两个句子中的“方便”用word2vec学习到的词向量就无法区分，因为word2vec学习的是一个固定的词向量，它只能用同一个词向量来表示一个词不同的语义，而elmo就能处理这种多义词的问题。

one hot 模型

词袋模型

缺点：稀疏；无序；纬度爆炸；每个向量都正交，相当于每个词都是没有关系的。

1.word2vec

word2vec解读

秒懂词向量Word2vec的本质

Word2Vec详解(这个更详细)

小白都能理解的通俗易懂word2vec详解 (两个模型的推导过程通俗易懂)

在 NLP 中，把 x 看做一个句子里的一个词语，y 是这个词语的上下文词语，那么这里的 f，便是 NLP 中经常出现的语言模型（language model），这个模型的目的，就是判断 (x,y) 这个样本，是否符合自然语言的法则，更通俗点说就是：词语x和词语y放在一起，是不是人话。
Word2vec 正是来源于这个思想，但它的最终目的，不是要把 f 训练得多么完美，而是只关心模型训练完后的副产物——模型参数（这里特指神经网络的权重），并将这些参数，作为输入 x 的某种向量化的表示，这个向量便叫做——词向量。

1.1 CBoW模型

CBoW模型等价于一个词袋模型的向量乘以一个Embedding矩阵，从而得到一个连续的embedding向量。

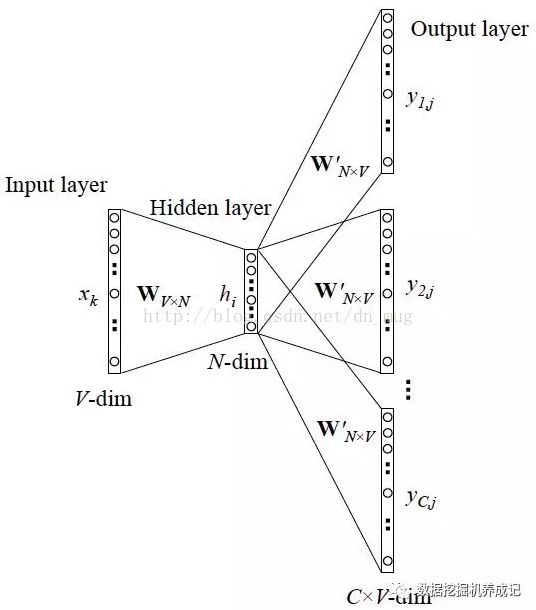
CBoW前向计算过程

词向量最简单的方式是one-hot方式。one-hot就是从很大的词库corpus里选V个频率最高的词(忽略其他的) ，V一般比较大，比如V＝10W，固定这些词的顺序，然后每个词就可以用一个V维的稀疏向量表示了，这个向量只有一个位置的元素是1，其他位置的元素都是0。在上图中，

Input layer (输入层)：是上下文单词的one hot。假设单词向量空间的维度为V，即整个词库corpus大小为V，上下文单词窗口的大小为C。
假设最终词向量的维度大小为N，则图中的权值共享矩阵为W。W的大小为 $V * N$ ，并且初始化。
假设语料中有一句话"我爱你"。如果我们现在关注"爱"这个词，令C=2，则其上下文为"我",“你”。模型把"我" "你"的onehot形式作为输入。易知其大小为 $1 * V$ 。C 个 $1 * V$ 大小的向量分别跟同一个 $V * N$ 大小的权值共享矩阵W相乘，得到的是C个 $1 * N$ 大小的隐层hidden layer。
C 个 $1 * N$ 大小的hidden layer取平均，得到一个 $1 * N$ 大小的向量，即图中的Hidden layer。
输出权重矩阵 $W^{'}$ 为 $N * V$ ，并进行相应的初始化工作。
将得到的Hidden layer向量 $1 * N$ 与W’相乘，并且用softmax处理，得到 $ 1*V $ 的向量，此向量的每一维代表corpus中的一个单词。概率中最大的index所代表的单词为预测出的中间词。
与groud truth中的one hot比较，求loss function的的极小值。

具体计算过程

从input -> hidden: $W^{T} ∗x$ ， $W$ 为 $V * N$ 矩阵， $x$ 为 $V * 1$ 向量，最终隐层的结果为 $N * 1$
从hidden -> output: $x^T∗W^′$ ，其中 $x$ 为 $N * 1$ 向量， $W^{'}$ 为 $V * N$ ，最终结果为 $1 * V$

1.2 Skip-gram模型

1.3 Tricks（层次softmax和负采样）

因为权值矩阵是一个非常大的矩阵，比如词典是10000，期望的词向量维度是300，那么这个矩阵就有300万参数，而这对于最后一层的softmax和反向传播都会带来极低的效率。因此以下两个技巧都是为了提升模型的速度。

1. 层softmax技巧（hierarchical softmax）
解释一：最后预测输出向量时候，大小是1*V的向量，本质上是个多分类的问题。通过hierarchical softmax的技巧，把V分类的问题变成了log(V)次二分类。

解释二：层次softmax的技巧是来对需要训练的参数的数目进行降低。所谓层次softmax实际上是在构建一个哈夫曼树，这里的哈夫曼树具体来说就是对于词频较高的词汇，它的树的深度就较浅，对于词频较低的单词的它的树深度就较大。

总结： 层次softmax就是利用一颗哈夫曼树来简化原来的softmax的计算量。具体来说就是对词频较高的单词，他在哈夫曼树上的位置就比较浅，而词频较低的位置就在树上的位置比较深。

2. 负采样（negative sampling）
解释一：本质上是对训练集进行了采样，从而减小了训练集的大小。每个词的概率由下式决定：

$\frac{count(w)^{3/4}}{\sum\limits_{u \in vocab} count(u)^{3/4}}$

在训练每个样本时, 原始神经网络隐藏层权重的每次都会更新, 而负采样只挑选部分权重做小范围更新

解释二：
负采样主要解决的问题就是参数量过大，模型很难训练的问题。那么什么是负采样中的正例和负例？如果 vocabulary 大小为1万时，当输入样本 ( “fox”, “quick”) 到神经网络时， “ fox” 经过 one-hot 编码，在输出层我们期望对应 “quick” 单词的那个神经元结点输出 1（这就是正例），其余 9999 个都应该输出 0（这就是负例）。在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们称为 negative word. negative sampling 的想法也很直接，将随机选择一小部分的 negative words，比如选 10个 negative words 来更新对应的权重参数。

解释三：
Negative Sampling是对于给定的词,并生成其负采样词集合的一种策略,已知有一个词,这个词可以看做一个正例,而它的上下文词集可以看做是负例,但是负例的样本太多,而在语料库中,各个词出现的频率是不一样的,所以在采样时可以要求高频词选中的概率较大,低频词选中的概率较小,这样就转化为一个带权采样问题,大幅度提高了模型的性能。

1.4 CBOW和Skip-gram的区别

在cbow方法中，是用周围词预测中心词，从而利用中心词的预测结果情况，使用Gradient Desent方法，不断的去调整周围词的向量。当训练完成之后，每个词都会作为中心词，把周围词的词向量进行了调整，这样也就获得了整个文本里面所有词的词向量。要注意的是， cbow的对周围词的调整是统一的：求出的gradient的值会同样的作用到每个周围词的词向量当中去。因此，cbow预测行为的次数跟整个文本的词数几乎是相等的（每次预测行为才会进行一次back propgation, 而往往这也是最耗时的部分），复杂度大概是O(V)（每个单词的词向量调整V次）。

而skip-gram是用中心词来预测周围的词。在skip-gram中，会利用周围的词的预测结果情况，使用Gradient Decent来不断的调整中心词的词向量，最终所有的文本遍历完毕之后，也就得到了文本所有词的词向量。可以看出，skip-gram进行预测的次数是要多于cbow的：因为每个词在作为中心词时，都要使用周围词进行预测一次。这样相当于比cbow的方法多进行了K次（假设K为窗口大小），因此时间的复杂度为O(KV)（每个单词的词向量调整的次数是KV次，K是窗口的大小，V是语料库中单词的数量），训练时间要比cbow要长。

但是在skip-gram当中，每个词都要收到周围的词的影响，每个词在作为中心词的时候，都要进行K次的预测、调整。因此， 当数据量较少，或者词为生僻词出现次数较少时，这种多次的调整(skip-gram的训练方法)会使得词向量相对的更加准确。因为尽管cbow从另外一个角度来说，某个词也是会受到多次周围词的影响（多次将其包含在内的窗口移动），进行词向量的跳帧，但是他的调整是跟周围的词一起调整的，grad的值会平均分到该词上，相当于该生僻词没有收到专门的训练，它只是沾了周围词的光而已。

因此，从更通俗的角度来说：
在skip-gram里面，每个词在作为中心词的时候，实际上是 1个学生 VS K个老师，K个老师（周围词）都会对学生（中心词）进行“专业”的训练，这样学生（中心词）的“能力”（向量结果）相对就会扎实（准确）一些，但是这样肯定会使用更长的时间；

cbow是 1个老师 VS K个学生，K个学生（周围词）都会从老师（中心词）那里学习知识，但是老师（中心词）是一视同仁的，教给大家的一样的知识。至于你学到了多少，还要看下一轮（假如还在窗口内），或者以后的某一轮，你还有机会加入老师的课堂当中（再次出现作为周围词），跟着大家一起学习，然后进步一点。因此相对skip-gram，你的业务能力肯定没有人家强，但是对于整个训练营（训练过程）来说，这样肯定效率高，速度更快。

1.5 总结

一句话：word2vec就是一系列的模型的权重。利用一个有监督方式来训练模型，利用模型中得到的权重来表示一个词。

另一种解释：word2vec是用一个一层的神经网络 (即CBOW) 把one-hot形式的稀疏词向量映射称为一个n维(n一般为几百)的稠密向量的过程。为了加快模型训练速度，其中的tricks包括Hierarchical softmax，negative sampling, Huffman Tree等。

1.6 QA

Q1： word2vec是如何解决oov问题的？
word2vec并没有解决oov问题。但是后续有很多解决的办法，例如

引入UNK，
所有的OOV词拆成字符(比如 Jessica，变成J，e，s，s，i，c，a)，
引入subwords(同样要进行拆词。不同的是，非OOV的词也要拆，并且非字符粒度，而是sub-word。还是 Jessica，变成Je，ssi，ca)，扩大词表。

Q2. 为什么要去除停用词
文档中如果大量使用Stop words容易对页面中的有效信息造成噪音干扰，所以适当地减少停用词出现的频率，可以有效地帮助我们提高关键词密度，让关键词更集中、更突出。

Q3. Negative Sampling是如何做的

Negative Sampling是对于给定的词,并生成其负采样词集合的一种策略,已知有一个词,这个词可以看做一个正例,而它的上下文词集可以看做是负例,但是负例的样本太多,而在语料库中,各个词出现的频率是不一样的,所以在采样时可以要求高频词选中的概率较大,低频词选中的概率较小,这样就转化为一个带权采样问题,大幅度提高了模型的性能。

Q4. word2vec是如何训练的

见上面

Q5. 针对生僻词，哪种训练方法更合适？

skip-gram模型更合适

当数据量较少，或者词为生僻词出现次数较少时，这种多次的调整会使得词向量相对的更加准确。因为尽管cbow从另外一个角度来说，某个词也是会受到多次周围词的影响（多次将其包含在内的窗口移动），进行词向量的跳帧，但是他的调整是跟周围的词一起调整的，反向传播梯度的值会平均分到该词上，相当于该生僻词没有收到专门的训练，它只是沾了周围词的光而已。

2.Glove

参考博文:

CSDN上的一个回答，讲解的比较全面

对损失函数做了一个简单的分析，可以作为对上面回答的一个补充

1. 概述

Glove融合了矩阵分解和全局统计信息的优势,统计语料库的词-词之间的共现矩阵,加快模型的训练速度而且又可以控制词的相对权重。

GloVe的全称叫Global Vectors for Word Representation，它是一个基于全局词频统计（count-based & overall statistics）的词表征（word representation）工具，它可以把一个单词表达成一个由实数组成的向量，这些向量捕捉到了单词之间一些语义特性，比如相似性（similarity）、类比性（analogy）等。我们通过对向量的运算，比如欧几里得距离或者cos相似度，可以计算出两个单词之间的语义相似性。

模型目标：进行词的向量化表示，使得向量之间尽可能多地蕴含语义和语法的信息。
输入：语料库
输出：词向量
方法概述：首先基于语料库构建词的共现矩阵，然后基于共现矩阵和GloVe模型学习词向量。

开始 -> 统计共现矩阵 -> 训练词向量 -> 结束

2. 什么是共现矩阵

设共现矩阵为X，其元素为Xi,j.

Xi,j 的意义为：在整个语料库中，单词i和单词 j 共同出现在一个窗口中的次数。

例子：

i love you but you love him i am sad

这个小小的语料库只有1个句子，涉及到7个单词：i、love、you、but、him、am、sad。
如果我们采用一个窗口宽度为5（左右长度都为2）的统计窗口，那么就有以下窗口内容：

窗口标号	中心词	窗口内容
0	i	i love you
1	love	i love you but
2	you	i love you but you
3	but	love you but you love
4	you	you but you love him
5	love	but you love him i
6	him	you love him i am
7	i	love him i am sad
8	am	him i am sad
9	sad	i am sad

窗口0、1长度小于5是因为中心词左侧内容少于2个，同理窗口8、9长度也小于5。

以窗口5为例说明如何构造共现矩阵：

2.1 共现矩阵的一个更直观例子

Corpus:
1. I like deep learning.
2. I like NLP.
3. I enjoy flying.

从语料库包含的单词为：I、 like、 deep、 learning、 NLP、 enjoy、 flying. 假设window length 为1. 那么这个语料库的共现矩阵便如下图所示：

共现矩阵存在的问题:

面临稀疏性问题、
向量维数随着词典大小线性增长。

为了解决维度过大的问题，Glove的提出者采用一个特殊的方法（由于数学知识有限，这个方法并没有理解，所以暂且忽略这个降维的过程）进行降维。

3. 代价函数

$J=\sum_{i,j}^Nf(X_{i,j})(v_{i}^Tv_{j}+b_{i}+b_{j}-log(X_{i,j}))^2$

$v_i,v_j$ 是单词i和单词j的词向量， $b_i,b_j$ 是两个标量（作者定义的偏差项），f是权重函数，N是词汇表的大小（共现矩阵维度为N*N）， $X_{i,j}$ 代表共现矩阵中由 i 和 j 定位到的数值。

4. Glove是如何训练的

GloVe是一种无监督（unsupervised learing）的学习方式（因为它确实不需要人工标注label），但其实它还是有label的，这个label就是以上公式中的 $log(X_{ij})$ ，而公式中的向量 $v_{i},v_{j}$ 就是要不断更新学习的参数，所以本质上它的训练方式跟监督学习的训练方法没什么不一样，都是基于梯度下降的。

具体地，论文里的实验是这么做的：采用了AdaGrad的梯度下降算法，对矩阵 X 中的所有非零元素进行随机采样，学习曲率（learning rate）设为0.05，在vector size小于300的情况下迭代了50次，其他大小的vectors上迭代了100次，直至收敛。最终学习得到的是两个vector是 $v_{i}, v_{j}$ ，因为 X 是对称的（symmetric），所以从原理上讲 $v_{i}, v_{j}$ 是也是对称的，他们唯一的区别是初始化的值不一样，而导致最终的值不一样。

5. Glove和LSA、word2vec的区别

LSA（Latent Semantic Analysis）是一种比较早的count-based的词向量表征工具，它也是基于co-occurance matrix的，只不过采用了基于奇异值分解（SVD）的矩阵分解技术对大矩阵进行降维，而SVD的复杂度是很高的，所以它的计算代价比较大。还有一点是它对所有单词的统计权重都是一致的。而这些缺点在GloVe中被一一克服了。
而word2vec最大的缺点则是没有充分利用所有的语料，所以GloVe其实是把两者的优点结合了起来。从这篇论文给出的实验结果来看，GloVe的性能是远超LSA和word2vec的，但网上也有人说GloVe和word2vec实际表现其实差不多。

6. QA

Q1: 未训练之前的词向量是用什么进行表示的
比如说要训练维度300的词向量，未训练之前就是随机初始化的N个300维的词向量。

Q2. Glove和skip-gram、CBOW模型对比

3.ELMo

ELMo超详细解读

ELMo论文解读——原理、结构及应用

ELMo的使用

史上最全词向量讲解（LSA/word2vec/Glove/FastText/ELMo/BERT）

ELMo原理解析及简单上手使用

李宏毅的视频，对于训练的过程和使用的过程讲的很清楚

word2vec和Glove词向量表征的缺点是对于每一个单词都有唯一的一个embedding表示, 也就是在训练完成以后，一个文本中相同的token就具有相同的词向量表征，而对于多义词显然这种做法不符合直觉，但是单词的意思又和上下文相关, ELMo的做法是我们只预训练language model，而word embedding是通过输入的句子实时输出的，这样单词的意思就是上下文相关的了，这样就很大程度上缓解了歧义的发生.

在此之前的 Word Embedding 本质上是个静态的方式，所谓静态指的是训练好之后每个单词的表达就固定住了，以后使用的时候，不论新句子上下文单词是什么，这个单词的 Word Embedding 不会跟着上下文场景的变化而改变，所以对于比如 Bank 这个词，它事先学好的 Word Embedding 中混合了几种语义，在应用中来了个新句子，即使从上下文中（比如句子包含 money 等词）明显可以看出它代表的是「银行」的含义，但是对应的 Word Embedding 内容也不会变，它还是混合了多种语义。这是为何说它是静态的，这也是问题所在。

ELMO 本身是个根据当前上下文对 Word Embedding 动态调整的思路

word2vec和glove是固定好的词向量，一个语料库中同样的单词只能对应一个embedding，其包含了各种的语义关系，这对于多义词是不友好的。而ELMo是动态的产生一句话中所有token对应的词向量，ELMo的输入就是一句话，得到每句话中每个token对应的embedding，因此相同的token可能有不同的embedding。

1. ELMo的结构

Elmo主要使用了一个两层双向的LSTM语言模型

左边前向LSTM中输入的是句子的上文，右边后向LSTM中输入的是句子的下文。训练好之后以三层内部状态的函数来表示词向量。

2. 模型参数

2层biLSTM；
BiLSTM层向量维度4096维；
投影层词向量维度：512维。
从最底层词嵌入层到第一层biLSTM输出层之间还有一个残差链接。

最终模型输入的是128个句子（一批）正反向512维的词向量，词向量经过字符卷积得到，每个句子截断为20个词，不足的补齐。

以"I love China very much"为例，如果要预测的 $T 1$ 是love，那么 $E 1$ 处输入的就是"I"和"China".

3. 字符卷积

4. 残差网络

4.1 目的
解决深度神经网络中训练困难的问题。

4.2 原理
使用门控单元，使输入以一定的比例穿过网络，增加网络的灵活性。

5. ELMO是如何得到词向量的

最后的词向量是三个词向量的结合：初始化词向量，第一层BiLSTM的输出，第二层BiLSTM的输出，三者加权求和得到最后的词向量。这三层词向量都被scale到了1024维。

1.为什么使用三层的输出加权求和得到最后的词向量？

这里之所以将3层的输出都作为token的embedding表示是因为实验已经证实不同层的LM输出的信息对于不同的任务作用是不同的，也就是所不同层的输出捕捉到的token的信息是不相同的。

4.Transformer

一些关于BERT的问题整理记录

一些关于Transformer问题整理记录

一些关于ELMo问题整理记录

知乎上相当漂亮的一个回答

BERT大火却不懂Transformer？读这一篇就够了

理解Transformer的三层境界–Attention is all you need

李宏毅的视频，对于训练的过程和使用的过程讲的很清楚

4.1 self-attention

$softmax(\frac{Q^TK}{\sqrt{d_{k}}})V$

其中的 $d_{k}$ 代表的是 $K$ 的维度,原文中是64.

X矩阵中的每一行代表一个单词的词向量，其中的 $W^Q, W^K, W^V$ 都是随机初始化的权重矩阵

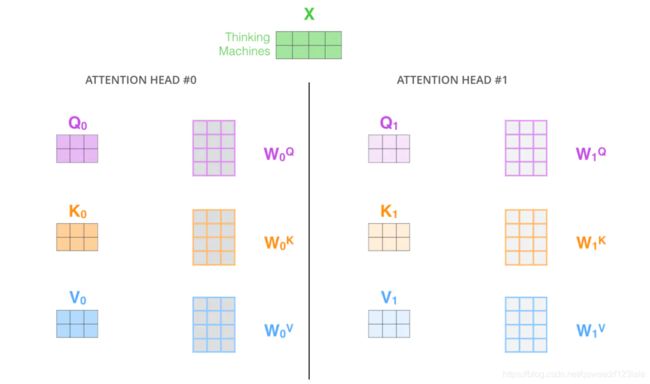
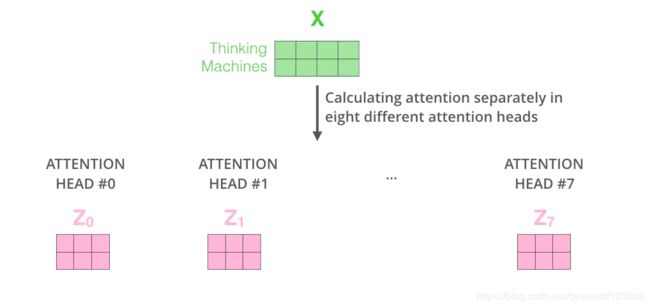
4.2 multi-head机制

Multi-headed 的机制是为了完善self-attention的性能提出来的。他的能力主要体现在两个方面：

扩展了模型专注于不同位置的能力。由于在得到的self-attention的输出中，他可能实际上更多的被自身支配，这时候就需要multi-head来改善。
它给出了注意力层的多个“表示子空间”（representation subspaces）。对于“多头”注意机制，我们有多个 Q/K/V 矩阵集(Transformer使用八个注意力头，因此我们对于每个编码器/解码器有八个矩阵集合)。这些集合中的每一个都是随机初始化的，在训练之后，每个集合都被用来将输入词嵌入(或来自较低编码器/解码器的向量)投影到不同的表示子空间中。

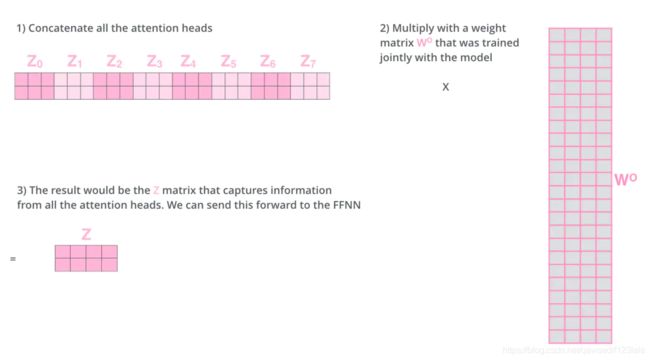
对于上述8个Z，我们需要把他压缩为一个Z，如下图所示

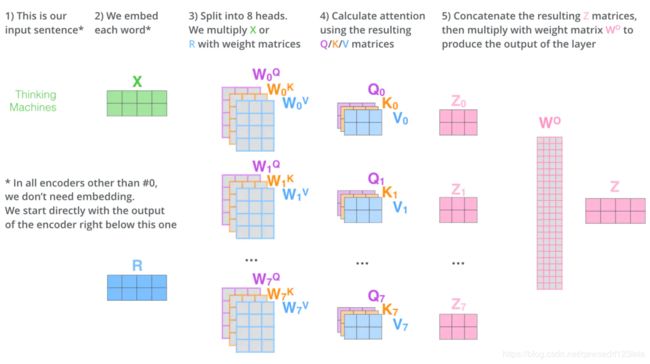
4.3 序列顺序-位置编码

Transformer中的位置编码是由cos/sin位置函数产生的，BERT是随机产生的。由于BERT的语料库非常大并且参数量非常大，这就使得随机位置向量可以得到学习。最后实验表明这和Transformer中的cos/sin位置函数生成的位置向量效果相同。

4.4 残差网络

残差网络主要是链接两个self-attention层。他就是把单元的输入直接与单元输出加在一起，然后再做下游的任务。

在Transformer中的应用如下

4.5 Transformer介绍

Transformer本身是一个encoder-decoder模型，那么也就可以从encoder和decoder两个方面介绍。

对于encoder，原文是由6个相同的大模块组成，每一个大模块内部又包含多头self-attention模块和前馈神经网络模块。尤其是对于多头self-attention模块相对与传统的attention机制能更关注输入序列中单词与单词之间的依赖关系，让输入序列的表达更加丰富。同时这里的encoder模块也是BERT的一个主要的组成模块。

对于decoder模块，原文中也是包含了6个相同的大模块，每一个大模块由self-attention模块，encoder-decoder交互模块以及前馈神经网络模块三个子模块组成。其self-attention模块和前馈神经网络模块和encoder端是一致的；对于encoder和decoder模块有点类似于传统的attention机制，目的就在于让Decoder端的单词(token)给予Encoder端对应的单词(token)“更多的关注(attention weight)”。

注意decoder中的K和V来自于encoder

4.6 QA

Q1. Transformer Decoder端的输入具体是什么

对于第一个大模块，简而言之，其训练及测试时接收的输入为：

训练的时候每次的输入为上次的输入加上输入序列向后移一位的ground truth (例如每向后移一位就是一个新的单词，那么则加上其对应的embedding)，特别地，当decoder的time step为1时(也就是第一次接收输入)，其输入为一个特殊的token，可能是目标序列开始的token(如)，也可能是源序列结尾的token(如)，也可能是其它视任务而定的输入等等，不同源码中可能有微小的差异，其目标则是预测下一个位置的单词(token)是什么，对应到time step为1时，则是预测目标序列的第一个单词(token)是什么，以此类推；
这里需要注意的是，在实际实现中可能不会这样每次动态的输入，而是一次性把目标序列的embedding通通输入第一个大模块中，然后在多头attention模块对序列进行mask即可，

这里为什么要进行mask，因为我们需要对后面的序列进行预测，在训练的时候，后面的序列信息对前面是不可知的，所以需要把后面的序列进行sequence mask。
在测试的时候，是先生成第一个位置的输出，然后有了这个之后，第二次预测时，再将其加入输入序列，以此类推直至预测结束。

简而言之：1）训练时每次的输入是上一时刻输出加上输入序列的后移一位的ground truth；2）测试时是先生成第一个位置的输出，然后有了这个以后，第二次预测时再将其加入到输入序列，以此类推直至预测结束。

Q2. 什么是sequence mask
sequence mask 是为了使得 decoder 不能看见未来的信息。也就是对于一个序列，在 time_step 为 t 的时刻，我们的解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。因此我们需要想一个办法，把 t 之后的信息给隐藏起来。

Q3. encoder和decoder端的self-attention有什么不同
Decoder端的多头self-attention需要做mask，因为它在预测时，是“看不到未来的序列的”，所以要将当前预测的单词(token)及其之后的单词(token)全部mask掉。

Q4. self-attention为什么有用
self-attention可以捕获同一个句子中单词之间的一些句法特征或者语义特征。引入Self Attention后会更容易捕获句子中长距离的相互依赖的特征，如果是RNN或者LSTM，需要依次序序列计算，对于远距离的相互依赖的特征，要经过若干时间步步骤的信息累积才能将两者联系起来，而距离越远，有效捕获的可能性越小。但是Self Attention在计算过程中会直接将句子中任意两个单词的联系通过一个计算步骤直接联系起来，所以远距离依赖特征之间的距离被极大缩短，有利于有效地利用这些特征。

Q5. 为什么需要multi-head attention
因为只是用一个self-attention，当前单词可能会起一个主导作用，其他文本信息会被削弱。multi-head attention会形成多个子空间，扩展了模型专注于不同位置的能力，然后再将各方面的信息综合起来，着有助于网络捕捉到更丰富文本特征。

Q6. Transformer相对于seq2seq的优点

加入了self-attention，这样使得源序列和目标序列首先自联起来。然后通过encoder-decoder交互模块把两者联系起来；
transformer的并行计算能力远超seq2seq（他的并行能力主要体现在self-attention）。

Q7. Transformer是如何并行计算的
其并行能力主要体现在self-attention模块，因为对与某个序列 $x_1,x_2,...x_n$ ，self-attention可以直接计算 $x_i,x_j$ 的结果，而RNN模型必须按照顺序计算。

Q8. Transformer中句子的encoder表示是什么？如何加入词序信息的？
Encoder端得到的是整个输入序列的encoding表示，其中最重要的是经过了self-attention模块，让输入序列的表达更加丰富，而加入词序信息是使用不同频率的正弦和余弦函数。

Q9. Transformer中的FFNN两种构成方式的区别
一种是传统的DNN，一种是CNN（CNN也是前馈神经网络）

Q10. layer nomalization的before和after的区别（其实就是nomarlization层需放在激活函数前面还是后面的问题）

Pre-LN相较传统Transformer的Post-LN在训练阶段可以不需要warm-up并且收敛更快。

5.BERT

一些关于BERT的问题整理记录

一些关于Transformer问题整理记录

一些关于ELMo问题整理记录

BERT原理介绍

李宏毅的视频，对于训练的过程和使用的过程讲的很清楚

5.1 基本概念

什么是预训练模型
首先我们要了解一下什么是预训练模型，举个例子，假设我们有大量的维基百科数据，那么我们可以用这部分巨大的数据来训练一个泛化能力很强的模型，当我们需要在特定场景使用时，例如做文本相似度计算，那么，只需要简单的修改一些输出层，再用我们自己的数据进行一个增量训练，对权重进行一个轻微的调整。

预训练的好处在于在特定场景使用时不需要用大量的语料来进行训练，节约时间效率高效，bert就是这样的一个泛化能力较强的预训练模型，也就是得到模型参数，然后实时输出句子中每个token的embedding，类似于ELMo；

5.2 BERT模型

5.2.1 结构
BERT的内部结构，官网提供了两个版本，L表示的是transformer的层数，H表示输出的维度，A表示mutil-head attention的个数
$BERT_{BASE}:L=12,H=768,A=12,Total Parameters=110M$
$BERT_{LARGE}:L=24, H=1024, A=16, Total Parameters=340M$
从模型的层数来说其实已经很大了，但是由于transformer的residual模块，层数并不会引起梯度消失等问题，但是并不代表层数越多效果越好，有论点认为低层偏向于语法、句法特征学习，高层偏向于语义特征学习，因此使用的时候可以适当调整BERT的层数。

5.2.2 BERT的训练过程
BERT的预训练阶段采用了两个独有的非监督任务，一个是Masked Language Model，还有一个是Next Sentence Prediction。

第一个任务是采用MaskLM的方式来训练语言模型，通俗地说就是在输入一句话的时候，随机地选一些要预测的词，然后用一个特殊的符号[MASK]来代替它们，之后让模型根据所给的标签去学习这些地方该填的词。

第二个任务在双向语言模型的基础上额外增加了一个句子级别的连续性预测任务，即预测输入BERT的两段文本是否为连续的文本.

1） Masked Language Model
mlm可以理解为完形填空，作者会随机mask每一个句子中15%的词，用其上下文来做预测，例如：my dog is hairy → my dog is [MASK]
此处将hairy进行了mask处理，然后采用非监督学习的方法预测mask位置的词是什么，但是该方法有一个问题，因为是mask15%的词，其数量已经很高了，这样就会导致某些词在fine-tuning阶段从未见过，为了解决这个问题，作者做了如下的处理：

80%的时间是采用[mask]，my dog is hairy → my dog is [MASK]
10%的时间是随机取一个词来代替mask的词，my dog is hairy -> my dog is apple
10%的时间保持不变，my dog is hairy -> my dog is hairy

那么为啥要以一定的概率使用随机词呢？这是因为transformer要保持对每个输入token分布式的表征，否则Transformer很可能会记住这个[MASK]就是"hairy"。至于使用随机词带来的负面影响，文章中说了,所有其他的token(即非"hairy"的token)共享15%*10% = 1.5%的概率，其影响是可以忽略不计的。

2）Next Sentence Prediction
选择一些句子对A与B，其中50%的数据B是A的下一条句子，剩余50%的数据B是语料库中随机选择的，学习其中的相关性，添加这样的预训练的目的是目前很多NLP的任务比如QA和NLI都需要理解两个句子之间的关系，从而能让预训练的模型更好的适应这样的任务。

5.2.3 模型的输入和输出
BERT的输入可以是单一的一个句子或者是句子对，实际的输入值包括了三个部分，分别是token embedding词向量，segment embedding句向量，每个句子有个句子整体的embedding项对应给每个单词，还有position embedding位置向量，这三个部分相加形成了最终的bert输入向量。

5.3 BERT的损失函数

BERT的损失函数由两部分组成，第一部分是来自 Mask-LM 的单词级别分类任务，另一部分是句子级别的分类任务。通过这两个任务的联合学习，可以使得 BERT 学习到的表征既有 token 级别信息，同时也包含了句子级别的语义信息。具体损失函数如下：
$L(\theta, \theta_{1}, \theta_{2}) = L_{1}(\theta, \theta_1)+L_{2}(\theta, \theta_{2})$

其中 $\theta$ 是BERT中Encoder部分的参数， $\theta_1$ 是 Mask-LM 任务中在 Encoder 上所接的输出层中的参数， $\theta_2$ 则是句子预测任务中在 Encoder 接上的分类器参数。因此，在第一部分的损失函数中，如果被 mask 的词集合为 M，因为它是一个词典大小 |V| 上的多分类问题，那么具体说来有：
$L_{1}(\theta,\theta_{1}) = -\sum{_{i=1}^M}log p(m=m_{i}|\theta,\theta_{1}), m_{i} \in [1, 2,...,|V|]$
在句子中预测任务中，也是一个分类问题的损失函数：
$L_{2}(\theta,\theta_{2}) = -\sum{_{j=1}^N}log p(n=n_{j}|\theta,\theta_{2}), n_{i}[IsNext, NotNext]$
$L(\theta, \theta_{1}, \theta_{2}) = -\sum{_{i=1}^M}log p(m=m_{i}|\theta,\theta_{1})-\sum{_{j=1}^N}log p(n=n_{j}|\theta,\theta_{2})$

5.4 QA

Q1. 为什么BERT的效果比ELMo好，两者有什么区别？

LSTM的特征抽取能力远弱于Transformer
BERT的训练数据和模型参数均多余ELMo

ELMo模型是通过语言模型任务得到句子中单词的embedding表示，以此作为补充的新特征给下游任务使用。因为ELMO给下游提供的是每个单词的特征形式，所以这一类预训练的方法被称为“Feature-based Pre-Training”。而BERT模型是“基于Fine-tuning的模式”，这种做法和图像领域基于Fine-tuning的方式基本一致，下游任务需要将模型改造成BERT模型，才可利用BERT模型预训练好的参数。

Q2. BERT模型为什么要用mask?
BERT通过在输入X中随机Mask掉一部分单词，然后预训练过程的主要任务之一是根据上下文单词来预测这些被Mask掉的单词，那些被Mask掉的单词就是在输入侧加入的所谓噪音。类似BERT这种预训练模式，被称为DAE LM。因此总结来说BERT模型 [Mask] 标记就是引入噪音的手段。

关于DAE LM预训练模式，优点是它能比较自然地融入双向语言模型，同时看到被预测单词的上文和下文，然而缺点也很明显，主要在输入侧引入 [Mask] 标记，导致预训练阶段和Fine-tuning阶段不一致的问题。

另一种解释：

这样相当于添加一个噪声，预测一个词汇时，模型并不知道输入对应位置的词汇是否为正确的词汇（ 10% 概率），这就迫使模型更多地依赖于上下文信息去预测词汇，并且赋予了模型一定的纠错能力。

Q3. mask和CBOW不一致的地方
相同点：

CBOW的核心思想是：给定上下文，根据它的上文 Context-Before 和下文 Context-after 去预测input word。而BERT本质上也是这么做的，但是BERT的做法是给定一个句子，会随机Mask 15%的词，然后让BERT来预测这些Mask的词。

不同点：

首先，在CBOW中，每个单词都会成为input word，而BERT不是这么做的，原因是这样做的话，训练数据就太大了，而且训练时间也会非常长。
其次，对于输入数据部分，CBOW中的输入数据只有待预测单词的上下文，而BERT的输入是带有[MASK] token的“完整”句子，也就是说BERT在输入端将待预测的input word用[MASK] token代替了。
另外，通过CBOW模型训练后，每个单词的word embedding是唯一的，因此并不能很好的处理一词多义的问题，而BERT模型得到的word embedding(token embedding)融合了上下文的信息，就算是同一个单词，在不同的上下文环境下，得到的word embedding是不一样的。

Q4. BERT的embedding向量如何的来的
以中文为例，BERT模型通过查询字向量表将文本中的每个字转换为一维向量，作为模型输入(还有position embedding和segment embedding)；模型输出则是输入各字对应的融合全文语义信息后的向量表示。

而对于输入的token embedding、segment embedding、position embedding都是随机生成的，需要注意的是在Transformer论文中的position embedding由sin/cos函数生成的固定的值，而在这里代码实现中是跟普通 word embedding 一样随机生成的，可以训练的。**作者这里这样选择的原因可能是BERT训练的数据比Transformer那篇大很多，完全可以让模型自己去学习 **(这就是为什么BERT的位置向量是随机生成的)。

Q5. multi-head attention的具体结构

这里面Multi-head Attention其实就是多个Self-Attention结构的结合，每个head学习到在不同表示空间中的特征，如下图所示，两个head学习到的Attention侧重点可能略有不同，这样给了模型更大的容量。

针对一个具体的输入，初始化多个QKV矩阵，再BERT-large当中是12个，然后相当于做12次的self-attention，把最后的结果进行拼接，得到一个768维度的输出，然后通过一个权重矩阵 $W^0$ 进行处理得到最后的multi-head attention层的输出。

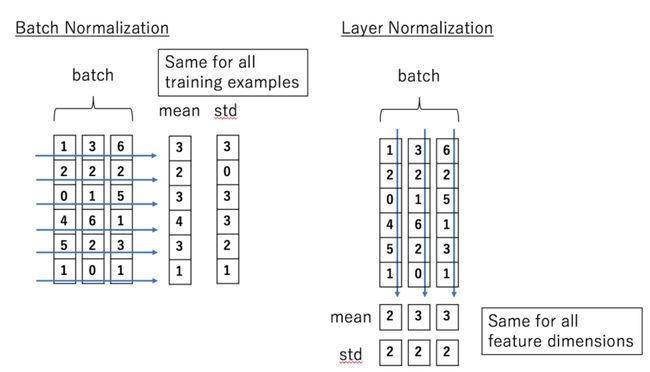
Q6. Bert 采用哪种Normalization结构，LayerNorm和BatchNorm区别，LayerNorm结构有参数吗，参数的作用

采用LayerNorm结构，和BatchNorm的区别主要是做规范化的维度不同，
BatchNorm针对一个batch里面的数据进行规范化，针对单个神经元进行，比如batch里面有64个样本，那么规范化输入的这64个样本各自经过这个神经元后的值（64维），
LayerNorm则是针对单个样本，不依赖于其他数据

BN和LN的区别

Batch Normalization 的处理对象是对一批样本， Layer Normalization 的处理对象是单个样本。

Batch Normalization 是对这批样本的同一维度特征做归一化， Layer Normalization 是对这单个样本的所有维度特征做归一化。

BN是纵向的做normalization，LN是横向的做normalization

Q7. transformer attention的时候为什么要除以 $\sqrt{d_{k}}$

至于attention后的权重为啥要除以，作者在论文中的解释是点积后的结果大小是跟维度成正比的，所以经过softmax以后，梯度就会变很小，除以后可以让attention的权重分布方差为1，而不是。

Q8. wordpice的作用

主要就是为了降低OOV的情况

Q9. 如何优化BERT的效果

扩增数据库，针对不同的问题选择合适的数据库等
BERT上面加一些结构，比如attention、rcnn等
改进预训练，在特定的大规模数据上预训练，利用等数据训练的更适合的任务，以及在训练后续mask的时候去mask低频词或者实体词等

Q10. 如何优化BERT的性能

ALBERT 做了一些改进优化，主要是不同层之间共享参数，以及用矩阵分解降低embedding的参数

Q11. Bert的位置embedding为什么要随机初始化，而不是sin/cos得到
由于BERT训练的语料库非常大，并且参数比较多，通过经验公式计算和随机初始化让网络学习到的位置编码效果几乎一样，而随机初始化更方便，所以使用随机初始化。

Q12. BERT为什么好用

训练数据量大
参数多

Q13. BERT得一些缺点

BERT在训练得时候需要随机mask掉一些词，但是这些词之间可能试有联系的，但是被mask掉以后iu无法得到他们之间的联系
BERT的在预训练时会出现特殊的[MASK]，但是它在下游的fine-tune中不会出现，这就出现了预训练阶段和fine-tune阶段不一致的问题。

6.XLNet

7. GPT

GPT和BERT类似，都是用的了transformer的encoder，但是GPT只是考虑了上文而没有考虑下文，训练的trick也不太一样。

8. GPT-2

采用的是transformer的decoder模块

QA

Q1. oov问题如何解决

word2vec本质上没有解决OOV的问题，fasttext解决了OOV的问题，因为引入了subwords，Glove本质上也是没解决OOV问题，ELMo只是利用上下文来Embedding词向量，解决一词多义的问题。如果要改进的话就可以加入WordPiece或者BPE的方法。

中文解决OOV，可用大规模预训练的bert，基于字的embedding。

Q2. CNN/RNN/LSTM/Transformer比较

特征抽取器的比较（CNN/RNN/LSTM/Transformer）

RNN

对于RNN，他主要能考虑到了序列信息，对于当前时刻输入的单词的词向量，他会利用tanh激活函数结合之前的文本序列信息来得到当前时刻的状态或者输出。在encoder-decoder模型中，他会把之前所有的序列信息加入到隐藏层来得到最后的decoder的输入。但是针对较短的文本序列问题，RNN可以有效的抓住之前的开始的文本序列信息。但是如果序列很长，这种线性序列结构在反向传播的时候容易导致严重的梯度消失或梯度爆炸问题

LSTM

LSTM的提出主要是为了解决长依赖问题和针对RNN的梯度消失的问题。LSTM的实现主要就是门机制，主要包括遗忘门，输入门，输出门三个门。在门控机制中的遗忘门中，通过sigmoid函数来决定需要遗忘上一个状态中哪些信息，在输入门中通过sigmoid函数结合当前输入和上一时刻的状态输出来决定更新cell中的信息。从宏观上来看，LSTM中有一个cell单元贯穿始终，使得中间状态信息直接向后传播。因此这使得LSTM可以有效的解决长依赖问题。

但是一个主要的问题是RNN和LSTM等序列模型在计算当前时刻的信息时需要加入之前一个时刻的的隐藏层状态信息。由于整个模型是一个序列依赖关心，这也就限制了整个模型必须是串行计算，无法并行计算。

CNN

对于CNN，他的实现或者说特征提取主要靠卷积层来提取特征，池化层来选择特征，然后使用全连接层来分类。其中卷积层提取特征主要是依靠卷积核对输入做卷积就可以得到特征。那么池化层一般选择使用最大池化来提取最主要的特征，在后面的全连接层中根据提取到的特征进行分类或者其他一些操作。但是卷积层中的CNN因为卷积核的存在，他依旧类似于N-gram，但是Dilated CNN的出现，使得CNN不是连续捕获特征，而是类似于跳一跳方式扩大捕获特征的距离。对位置信息敏感的序列可以抛弃掉max_pooling层。相对于LSTM， CNN的主要优势在于并行的能力。首先对于某个卷积核来说，每个滑动窗口位置之间没有依赖关系，所以可以并行计算；另外，不同的卷积核之间也没什么相互影响，所以也可以并行计算。

Transformer

针对Transformer，首先他打破了CNN和RNN框架。原文中主要是介绍self-attention的作用，但是核multi-attention、FFNN等也有很大的作用。Transformer也是跟CNN一样限定了句子的最大长度，句子长度不足的采用0进行padding。在self-attention中，他打破了序列信息，而是当前单词可以和句子中任意一个单词编码，集成到embedding里面去，此外transformer利用sin/cos位置函数来进行位置编码。（Bert等模型则给每个单词一个Position embedding，随机初始化的）。针对长距离依赖特征的问题，Self -attention天然就能解决这个问题，因为在集成信息的时候，当前单词和句子中任意单词都发生了联系。所以Transformer也是支持并行计算的。

CNN和LSTM如何选择？

CNN 和 LSTM是深度学习中使用最多，最为经典的两个模型，在NLP中，他们都可以用于提取文本的上下文特征，实际任务中该如何选择呢？实际中我们主要考虑三个因素：

上下文的依赖长度：
CNN 提取的是类似于n-gram的局部的上下文特征，LSTM由于三个门限单元的加入使得它能够处理提取更长的上下文特征
位置特征：
CNN由于max_pooling, 移除了文本序列中的相对位置信息，LSTM的序列结构，使得LSTM天然保留了位置信息
效率：
CNN 没有序列上的前后依赖问题，可以高效的并行运算，而lstm由于存在序列上的传递依赖问题，效率上相比CNN要低

综合上面三个因素的比较，CNN比较适合上下文依赖较短且对相对位置信息不敏感的场景，如情感分析，情感分析里的一些难点如双重否定，在上下文中的距离都离得不远，LSTM适合需要长距离特征，且依赖相对位置信息的场景。

各个模型介绍

1. BERT

BERT本身是在Transformer的基础上提出的一个模型。那么BERT就是使用了Transformer的encoder模块来作为基本组成单元以全连接的方式来搭建的BERT模型。BERT的预训练过程是可以分为两个部分来看。第一是mask language model，另一个是next sentence prediction。

在 mask language model中是对当前输入的文本序列中15%的单词进行随机mask，然后用其上下文来做预测。但是该方法有一个问题，因为是mask15%的词，其数量已经很高了，这样就会导致某些词在fine-tuning阶段从未见过，为了解决这个问题，原文是采用了一个训练的技巧，在训练过程中80%的时间是使用mask代替该词，10%的时间是随机取一个词来代替mask，再10%的时间是保持不变。

注意一个点就是为什么要用随机词：主要因为Transformer要保持对每个输入token分布式的表征，否则Transformer很可能会记住这个[mask]就是某一个特定的单词。

在next sentence preddiction中是为每个文本序列添加一个头和尾，来预测第二个句子是否是第一个句子逻辑上的下一句。然后使用头部添加的[cls]来做进一步的处理得到预测结果。

在实际的训练过程中，以上两个模型是联合在一起训练的，BERT的loss函数也是两个子任务loss函数的相加。

BERT的输入是三种类型的词向量（segment embedding，position embedding，word embedding），BERT在训练的过程中，每一层学到的内容并不一样，在较低的层次学到的更多的是句法和语法信息，在较高的层次学到的更多的是语义信息，因此在实际使用的时候也可以根据不同的需求调整BERT的结构。

2. GPT

GPT采用的也是Transformer的encoder模型，但是他是单向的，只考虑了当前单词的上文，而没有考虑下文。

3. Transformer

Transformer本身是一个encoder-decoder模型，那么也就可以从encoder和decoder两个方面介绍。

4. ELMo

ELMO 本身是个根据当前上下文对 Word Embedding 动态调整的思路

之前的词向量缺点是对于每一个单词都有唯一的一个embedding表示, 而对于多义词显然这种做法不符合直觉，而单词的意思又和上下文相关, ELMo的做法是我们只预训练language model，而word embedding是通过输入的句子实时输出的，这样单词的意思就是上下文相关的了，这样就很大程度上缓解了歧义的发生.

在此之前的 Word Embedding 本质上是个静态的方式，所谓静态指的是训练好之后每个单词的表达就固定住了，以后使用的时候，不论新句子上下文单词是什么，这个单词的 Word Embedding 不会跟着上下文场景的变化而改变，所以对于比如 Bank 这个词，它事先学好的 Word Embedding 中混合了几种语义，在应用中来了个新句子，即使从上下文中（比如句子包含 money 等词）明显可以看出它代表的是「银行」的含义，但是对应的 Word Embedding 内容也不会变，它还是混合了多种语义。这是为何说它是静态的，这也是问题所在。

5. Glove

GloVe的全称叫Global Vectors for Word Representation，它是一个基于全局词频统计**（count-based & overall statistics）的**词表征（word representation）工具，它可以把一个单词表达成一个由实数组成的向量，这些向量捕捉到了单词之间一些语义特性，比如相似性（similarity）、类比性（analogy）等。我们通过对向量的运算，比如欧几里得距离或者cos/sin相似度，可以计算出两个单词之间的语义相似性。

四、神经网络模型

1.神经网络的正向和反向传播

神经网络详解，正向传播和反向传播

2.DNN

深度神经网络(DNN)

DNN也称之为多层感知机(MLP) (我认为就是多个简单的线性(Linear)层的叠加)

3.CNN

从此明白了卷积神经网络（CNN）

1. 卷积神经网络vs传统神经网络

其实现在回过头来看，CNN跟我们之前学习的神经网络，也没有很大的差别。传统的神经网络，其实就是多个FC层叠加起来。CNN，无非就是把FC改成了CONV和POOL，就是把传统的由一个个神经元组成的layer，变成了由filters组成的layer。

2. 参数共享机制

我们对比一下传统神经网络的层和由filters构成的CONV层：
假设我们的图像是8×8大小，也就是64个像素，假设我们用一个有9个单元的全连接层：

那这一层我们需要多少个参数呢？需要 64×9 = 576个参数（先不考虑偏置项b）。因为每一个链接都需要一个权重w

那我们看看 同样有9个单元的filter是怎么样的：

其实不用看就知道，有几个单元就几个参数，所以总共就9个参数！因为，对于不同的区域，我们都共享同一个filter，因此就共享这同一组参数。这也是有道理的，通过前面的讲解我们知道，filter是用来检测特征的，那一个特征一般情况下很可能在不止一个地方出现，比如“竖直边界”，就可能在一幅图中多出出现，那么 我们共享同一个filter不仅是合理的，而且是应该这么做的。

由此可见，参数共享机制，让我们的网络的参数数量大大地减少。这样，我们可以用较少的参数，训练出更加好的模型，典型的事半功倍，而且可以有效地 避免过拟合。同样，由于filter的参数共享，即使图片进行了一定的平移操作，我们照样可以识别出特征，这叫做 “平移不变性”。因此，模型就更加稳健了。

3. 连接的稀疏性

由卷积的操作可知，输出图像中的任何一个单元，只跟输入图像的一部分有关系：

而传统神经网络中，由于都是全连接，所以输出的任何一个单元，都要受输入的所有的单元的影响。这样无形中会对图像的识别效果大打折扣。比较，每一个区域都有自己的专属特征，我们不希望它受到其他区域的影响。

正是由于上面这两大优势，使得CNN超越了传统的NN，开启了神经网络的新时代。

4. 经典CNN模型

https://www.jianshu.com/p/4a84885f787a

4.RNN

知乎上对RNN及其变体非常好的一个解读

针对RNN的解读_英文解读

利用MLP来解释RNN

视频加动图讲解RNN、LSTM、GRU

利用GRU对随机文本做分类

4.1 RNN理解中的的相关问题和解释

Q1. 一个sentence是如何在词向量化后喂入到RNN的？

首先明确一个RNN的time_step是和句子中token的数量相同的。比如一个RNN定义的是10个time_step,那么这个句子必须值包含10个token，如果不够10个就用0进行padding。
接下来每一个time_step喂入一个词向量化后的token然后得到一个output，或者最后取一个隐藏层状态。

比如这里有一句话，sentence=“我爱我的国”。进行句字的分词后是: 我 /爱 /我的 /国。可以表示为4个n维的词向量，这里n取8表示。那么喂入到RNN的过程就如下图所示。这里有四个时间步，每个时间步分别喂入“我/ 爱/ 我的/ 国” 四个词向量。

Q2. 如何理解RNN中的time_steps?
上面的例子中可以看出time_step就是喂入数据的长度。此外还可以参照这个博客理解。

1.终于理解了RNN里面的time_step

4.2 RNN中涉及的公式推导

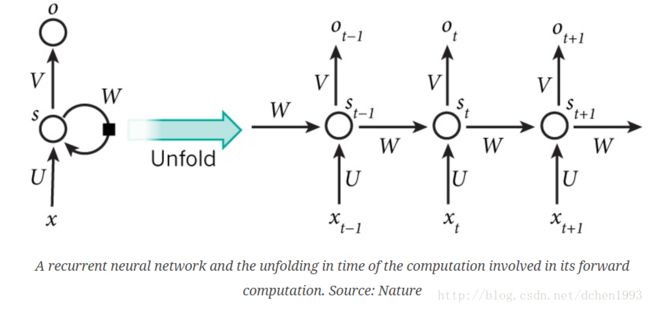
RNN的一个特点是所有的隐层共享参数(U,V,W)，整个网络只用这一套参数。

前向传播计算过程：
$s_{t} = tanh(Ux_{t}+Ws_{t-1})\\ o_{t} = softmax(Vs_{t})$

值得注意的是这里的激活函数tanh也可以换成ReLU，并且更换为ReLU可能会缓解梯度消失的问题，但是ReLU的输出比较大，可能进而导致梯度爆炸的问题。

4.3 RNN中存在的问题

Q1. 梯度消失
由于采用tanh激活函数，在训练的后期，梯度会变得比较小，如果几个趋于0的值相乘的话，乘积就会变得非常小，就会出现梯度消失现象。同样的情况也会出现在sigmoid函数。由于远距离的时刻的梯度贡献接近于0，因此很难学习到远距离的依赖关系。
解决方案：合适的参数初始化可以减少梯度消失的影响；使用ReLU激活函数；LSTM和GRU架构。

Q2. 梯度爆炸
如果后期的导数非常大，就会产生梯度爆炸的问题。
解决方案：既然在BP过程中会产生梯度消失（就是偏导无限接近0，导致长时记忆无法更新），那么最简单粗暴的方法，设定阈值，当梯度小于阈值时，更新的梯度为阈值。

5.LSTM

Understanding LSTM Networks

LSTM细节分析理解（pytorch版）

人人都能看懂的LSTM

LSTM模型与前向传播算法

难以置信！LSTM和GRU的解析从未如此清晰（动图+视频)

循环神经网络RNN、LSTM、GRU原理详解(这个文章对反向传播做了简单的解释)

为什么LSTM可以解决梯度消失的问题

5.1 RNN和LSTM的不同

相比于RNN， LSTM多出出来一个状态 $c^t$ （cell states）

5.2 LSTM内部结构

$\odot$ 表示矩阵对应元素相乘， $\oplus$ 代表矩阵对应元素相加
LSTM的三个阶段（也就是门机制）

忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。具体来说是通过计算得到的 $z^f$ （f表示forget）来作为忘记门控，来控制上一个状态的 $c^{t-1}$ 哪些需要留哪些需要忘。
选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 $x^t$ 进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的 z 表示。而选择的门控信号则是由 $z^i$ （i代表information）来进行控制。
输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $z^o$ 来进行控制的。并且还对上一阶段得到的 $c^o$ 进行了放缩（通过一个tanh激活函数进行变化）。

其中， $z^f$ ， $z^i$ ， $z^o$ 是由拼接向量乘以权重矩阵之后，再通过一个 sigmoid 激活函数转换成0到1之间的数值，来作为一种门控状态。而 z则是将结果通过一个 tanh 激活函数将转换成-1到1之间的值（这里使用 tanh 是因为这里是将其做为输入数据，而不是门控信号）。

5.3 LSTM门机制详解

遗忘门：以一定的概率控制是否遗忘上一层的cell状态.

$f^{t} = sigmoid(W_fh^{t-1}+U_{f}x^{t}+b_{f})$

输入门(也称选择性记忆门)：负责处理当前序列位置的输入。输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为 $i^t$ ,第二部分使用了 $t a n h$ 激活函数，输出为 $a^t$ , 两者的结果后面会相乘再去更新细胞状态。

$i^t = sigmoid(W_ih^{t-1}+U_{i}x^t+b_i)\\ a^t = tanh(W_ah^{t-1}+U_{a}x^t+b_a)$

细胞状态更新：在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态 $C^t$ 。我们来看看从细胞状态 $C^{t−1}$ 如何得到 $C^t$ 。

细胞状态 $C^t$ 由两部分组成，第一部分是 $C^{t−1}$ 和遗忘门输出 $f^t$ 的乘积，第二部分是输入门的 $i^t$ 和 $a^t$ 的乘积，即：
$c^t=c^{t-1}\odot f^t + i^t \odot a^t$
其中 $f^t$ 是遗忘门的输出

输出门（主要是考虑到有多少cell中的信息被加入到当前的输出状态（ $h_t$ ）中）隐藏状态 $h^t$ 的更新由两部分组成，第一部分是 $o^t$ , 它由上一序列的隐藏状态 $h^{t-1}$ 和本序列数据 $x^t$ ，以及激活函数sigmoid得到，第二部分由隐藏状态 $c^t$ 和tanh激活函数组成, 即：

$o^t = sigmoid(W_{o}h^{t-1}+U_ox^t+b_o)\\ h^t=o^t \odot tanh(c^t)$

LSTM的前向传播算法

5.4 LSTM的实际搭建过程

pytorch搭建LSTM框架的输出构成 ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200210105317796.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3Fhd3NlZHJmMTIzbGFsYQ==,size_16,color_FFFFFF,t_70) 知乎上的另一种图示 ### 5.5为什么LSTM可以解决RNN中梯度消失的问题

RNN为什么存在梯度消失的问题

在反向传播的过程中，梯度是连乘的，当梯度的数值小于1的时候，会导致远距离的梯度经过累乘后在当前时刻变得很小，进而发生梯度消失的问题。在反向传播的过程中，反向传播的公式有一个因式是参数W，如果W中有一个特征值特别大，就会产生梯度爆炸的问题。

LSTM是如何解决梯度消失的问题的

LTSM的解决梯度消失问题主要是通过cell单元。在LSTM内部，cell贯穿始终，并且在这条路径上只有乘和加，梯度是比较稳定的。其他路径上的梯度和RNN差不多，但是当其他路径发生梯度消失的时候，高速公路上的梯度没有消失，那么远距离的梯度就没有消失，也就缓解了梯度消失的问题。但是LSTM不能解决梯度爆炸的问题，因为在其他路径上发生了梯度爆炸，总的梯度依旧是爆炸的。

为什么不把RNN中的tanh激活函数换为ReLU？

ReLU可以在一定程度上缓解梯度消失的问题，但是有ReLU会导致非常大的输出，，最后的结果会变成多个W参数连乘，如果W中存在特征值>1，那么经过反向传播的连乘后就会产生梯度爆炸，RNN仍然无法传递较远的距离

RNN中的梯度消失和梯度爆炸

RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

“LSTM 能解决梯度消失/梯度爆炸”是对 LSTM 的经典误解。这里我先给出几个粗线条的结论，详细的回答以后有时间了再扩展：

首先需要明确的是，RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。
由 1 中所述的原因，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。
LSTM 中梯度的传播有很多条路径，这条路径上只有逐元素相乘和相加的操作，梯度流最稳定；但是其他路径（例如）上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。
LSTM 刚提出时没有遗忘门，或者说相当于，这时候在直接相连的短路路径上，可以无损地传递给，从而这条路径上的梯度畅通无阻，不会消失。类似于 ResNet 中的残差连接。
但是在其他路径上，LSTM 的梯度流和普通 RNN 没有太大区别，依然会爆炸或者消失。由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。
同样，因为总的远距离梯度 = 各条路径的远距离梯度之和，高速公路上梯度流比较稳定，但其他路径上梯度有可能爆炸，此时总的远距离梯度 = 正常梯度 + 爆炸梯度 = 爆炸梯度，因此 LSTM 仍然有可能发生梯度爆炸。不过，由于 LSTM 的其他路径非常崎岖，和普通 RNN 相比多经过了很多次激活函数（导数都小于 1），因此 LSTM 发生梯度爆炸的频率要低得多。实践中梯度爆炸一般通过梯度裁剪来解决。
对于现在常用的带遗忘门的 LSTM 来说，6 中的分析依然成立，而 5 分为两种情况：其一是遗忘门接近 1（例如模型初始化时会把 forget bias 设置成较大的正数，让遗忘门饱和），这时候远距离梯度不消失；其二是遗忘门接近 0，但这时模型是故意阻断梯度流的，这不是 bug 而是 feature（例如情感分析任务中有一条样本 “A，但是 B”，模型读到“但是”后选择把遗忘门设置成 0，遗忘掉内容 A，这是合理的）。当然，常常也存在 f 介于 [0, 1] 之间的情况，在这种情况下只能说 LSTM 改善（而非解决）了梯度消失的状况。
最后，别总是抓着梯度不放。梯度只是从反向的、优化的角度来看的，**多从正面的、建模的角度想想 LSTM 有效性的原因。**选择性、信息不变性都是很好的视角

5.5 QA

1.遗忘门是如何遗忘的
把t-1时的长期记忆输入 $C^{t-1}$ 乘上一个遗忘因子 $f^{t}$ 。遗忘因子是由短期记忆 $h^{t-1}$ 以及事件信息 $x^{t}$ 来计算。

2.为什么激活函数使用sigmoid和tanh
对于sigmoid函数，门是控制开闭的，全开时值为1，全闭值为０。有开有闭时，值在０到１之间。如果选择的激活函数得到的值不在０，１之间时，通常来说是没有意义的。
对于求值时的激活函数tanh，选取时与深层网络中激活函数选取是一样的，没有行与不行，只有好与不好。
所以，总结来说，门的激活函数只能是值域为０到１的，对于求值的激活函数无特殊要求。

3. RNN梯度消失问题，为什么LSTM和GRU可以解决此类问题

RNN为什么存在梯度消失的问题

LSTM是如何解决梯度消失的问题的

为什么不把RNN中的tanh激活函数换为ReLU？

ReLU可以在一定程度上缓解梯度消失的问题，但是有ReLU会导致非常大的输出，，最后的结果会变成多个W参数连乘，如果W中存在特征值>1，那么经过反向传播的连乘后就会产生梯度爆炸，RNN仍然无法传递较远的距离

RNN中的梯度消失和梯度爆炸

RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

“LSTM 能解决梯度消失/梯度爆炸”是对 LSTM 的经典误解。这里我先给出几个粗线条的结论，详细的回答以后有时间了再扩展：

1、首先需要明确的是，RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。

2、由 1 中所述的原因，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

3、LSTM 中梯度的传播有很多条路径，这条路径上只有逐元素相乘和相加的操作，梯度流最稳定；但是其他路径（例如）上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。

4、LSTM 刚提出时没有遗忘门，或者说相当于，这时候在直接相连的短路路径上，可以无损地传递给，从而这条路径上的梯度畅通无阻，不会消失。类似于 ResNet 中的残差连接。

5、但是在其他路径上，LSTM 的梯度流和普通 RNN 没有太大区别，依然会爆炸或者消失。由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。

6、同样，因为总的远距离梯度 = 各条路径的远距离梯度之和，高速公路上梯度流比较稳定，但其他路径上梯度有可能爆炸，此时总的远距离梯度 = 正常梯度 + 爆炸梯度 = 爆炸梯度，因此 LSTM 仍然有可能发生梯度爆炸。不过，由于 LSTM 的其他路径非常崎岖，和普通 RNN 相比多经过了很多次激活函数（导数都小于 1），因此 LSTM 发生梯度爆炸的频率要低得多。实践中梯度爆炸一般通过梯度裁剪来解决。

7、对于现在常用的带遗忘门的 LSTM 来说，6 中的分析依然成立，而 5 分为两种情况：其一是遗忘门接近 1（例如模型初始化时会把 forget bias 设置成较大的正数，让遗忘门饱和），这时候远距离梯度不消失；其二是遗忘门接近 0，但这时模型是故意阻断梯度流的，这不是 bug 而是 feature（例如情感分析任务中有一条样本 “A，但是 B”，模型读到“但是”后选择把遗忘门设置成 0，遗忘掉内容 A，这是合理的）。当然，常常也存在 f 介于 [0, 1] 之间的情况，在这种情况下只能说 LSTM 改善（而非解决）了梯度消失的状况。

8、最后，别总是抓着梯度不放。梯度只是从反向的、优化的角度来看的，**多从正面的、建模的角度想想 LSTM 有效性的原因。**选择性、信息不变性都是很好的视角

pytorch的实现：

官方API：
https://pytorch.org/docs/stable
nn.LSTM参数详解

参数
- input_size
- hidden_size
- num_layers
- bias
- batch_first
- dropout
- bidirectional
输入
- input (seq_len, batch, input_size)
- h_0 (num_layers * num_directions, batch, hidden_size)
- c_0 (num_layers * num_directions, batch, hidden_size)
输出
- output (seq_len, batch, num_directions * hidden_size)
- h_n (num_layers * num_directions, batch, hidden_size)
- c_n (num_layers * num_directions, batch, hidden_size)

GRU和LSTM的区别

GRU和LSTM的性能在很多任务上不分伯仲。
GRU 参数更少因此更容易收敛，但是数据集很大的情况下，LSTM表达性能更好。
从结构上来说，GRU只有两个门（update和reset），LSTM有三个门（forget，input，output），GRU直接将hidden state 传给下一个单元，而LSTM则用memory cell 把hidden state 包装起来。

6.Bi-LSTM

双向LSTM编码句子 ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200212105039486.png)

正向传播

反向传播

7.Attention机制

一文看懂 Attention 机制，你想知道的都在这里了

seq2seq中的Attention机制

深度学习中Attention Mechanism详细介绍：原理、分类及应用

动手推导Self-attention-译文

Attention机制的作用

Attention机制其实就是一系列注意力分配系数，也就是一系列权重参数。他的目的就是减少处理高维输入数据的计算负担,结构化的选取输入的子集,从而降低数据的维度。让系统更加容易的找到输入的数据中与当前输出信息相关的有用信息,从而提高输出的质量。帮助类似于decoder这样的模型框架更好的学到多种内容模态之间的相互关系。

7.1 attention机制

attention机制的数学表达式

直接照抄的参考博客2中的内容

利用双向RNN(LSTM)得到encoder中的hidden state $h_1, h_2, ..., h_T)$
假如当前的decoder的hidden state是 $s_{t-1}$ ，我们可以计算每一个输入位置j与当前输出位置的关联性，既 $e_{tj}=a(s_{t-1}, h_j)$ 写成向量的形式就是 $\vec{e_t}=(a(s_{t-1},h_1),...,a(s_{t-1},h_T))$ 其中的a是一种相关性的运算符，例如 $\vec{e_t}=\vec{s_{t-1}}^T\vec{h}$ 。
对 $\vec{e_t}$ 进行softmax操作，将其normalize得到attention的分布， $\vec{\alpha_t}=softmax(\vec{e_t})$ 。利用 $\vec{\alpha_t}$ 我们可以进行加权求和得到相应的context vector $\vec{c_t} = \sum_{j=1}^T\alpha_{tj}h_j$
由此，我们可以计算decoder的下一个hidden state $s_t = f(s_{t-1},y_{t-1},c_t)$ 以及该位置的输出 $p(y_t|y_1,...,y_{t-1}, \vec{x}) = g(y_{i-1}, s_i, c_i)$ （Tips: 这里不一定非要作用于decoder，也可以是其他的下游任务）

介绍下attention：

attention主要是在encoder-decoder模型中出现，原本的encoder-decoder模型的输出会关注输入的全部信息，而attention是希望关注和当前输出相关的重点局部内容。他的本质其实就是一系列的权重。

7.2 soft-attention

传统的Attention机制就是soft-attention。与之相对的是hard-attention，两者的不同如下：

Soft Attention是参数化的（Parameterization），因此可导，可以被嵌入到模型中去，直接训练。梯度可以经过Attention Mechanism模块，反向传播到模型其他部分。
Hard Attention是一个随机的过程。Hard Attention不会选择整个encoder的输出做为其输入，Hard Attention会依概率Si来采样输入端的隐状态一部分来进行计算，而不是整个encoder的隐状态。为了实现梯度的反向传播，需要采用蒙特卡洛采样的方法来估计模块的梯度。

由于soft-attention可以用于反向传播，现在用的attention基本都是soft-attention

7.3 self-attention

1.动手推导Self-attention-译文

self-attention和attention的不同：

传统的Attention是基于source端和target端的隐变量（hidden state）计算Attention的，得到的结果是源端的每个词与目标端每个词之间的依赖关系，而忽略了源端或目标端句子中词与词之间的依赖关系
但Self Attention不同，它分别在source端和target端进行，捕捉source端或target端自身的词与词之间的依赖关系；然后可以再把source端的得到的信息加入到target端中，这也就捕捉source端和target端词与词之间的依赖关系。所以相对于传统的Attention，他可以获取序列本身词与词之间的依赖关系，也可以得到source端和target端之间的关系。

8.TextCNN

https://bbs.dian.org.cn/topic/136/textcnn%E6%96%87%E6%9C%AC%E5%88%86%E7%B1%BB%E8%AF%A6%E8%A7%A3-%E4%BD%BF%E7%94%A8tensorflow%E4%B8%80%E6%AD%A5%E6%AD%A5%E5%B8%A6%E4%BD%A0%E5%AE%9E%E7%8E%B0%E7%AE%80%E5%8D%95textcnn(非常详细的一个博文)

9.DCNN

10. 残差网络

残差网络就是把输入加入到输出再进行下一步的处理。

11. 常见激活函数的优缺点

sigmoid函数

优点：
1. Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。
2. 连续函数，便于求导。
缺点：
1. sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象，意味着函数会变得很平，并且对输入的微小改变会变得不敏感。在反向传播时，当梯度接近于0，权重基本不会更新，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
2. sigmoid函数的输出不是0均值的，会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。
3. 计算复杂度高，因为sigmoid函数是指数形式。
tanh函数

tanh函数是 0 均值的，因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算的问题。
ReLU函数

优点：
1. 使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快。
2. 在x>0区域上，不会出现梯度饱和、梯度消失的问题。
3. 计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。
缺点：
1. ReLU的输出不是0均值的。
2. Dead ReLU Problem(神经元坏死现象)：ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。
产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

12. TF-IDF

TF-IDF算法原理及应用

词频（TF）表示词条（关键字）在文本中出现的频率。这个数字通常会被归一化(一般是词频除以文章总词数), 以防止它偏向长的文件。

逆向文件频率 (IDF) ：某一特定词语的IDF，可以由总文件数目除以包含该词语的文件的数目，再将得到的商取对数得到。如果包含词条t的文档越少, IDF越大，则说明词条具有很好的类别区分能力。

from nltk.text import TextCollection
from nltk.tokenize import word_tokenize
 
#首先，构建语料库corpus
sents=['this is sentence one','this is sentence two','this is sentence three']
sents=[word_tokenize(sent) for sent in sents] #对每个句子进行分词
print(sents)  #输出分词后的结果
corpus=TextCollection(sents)  #构建语料库
print(corpus)  #输出语料库
 
#计算语料库中"one"的tf值
tf=corpus.tf('one',corpus)    # 1/12
print(tf)
 
#计算语料库中"one"的idf值
idf=corpus.idf('one')      #log(3/1)
print(idf)
 
#计算语料库中"one"的tf-idf值
tf_idf=corpus.tf_idf('one',corpus)
print(tf_idf)

五、机器学习相关

1. bagging 和boosting的区别

样本选择上：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。
Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

样本权重上

Bagging：使用均匀取样，每个样例的权重相等
Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

预测函数：

Bagging：所有预测函数的权重相等。
Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

并行计算：

Bagging：各个预测函数可以并行生成
Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

偏差和方差

Bagging是降低方差
boosting是降低偏差

典型的bagging算法：RF

典型的boosting算法：Adaboost，提升树，GBDT，XGBoost

Bagging 是 Bootstrap Aggregating的简称，意思就是再取样 (Bootstrap) 然后在每个样本上训练出来的模型取平均，所以是降低模型的方差. Bagging 比如 Random Forest 这种先天并行的算法都有这个效果。
Boosting 则是迭代算法，每一次迭代都根据上一次迭代的预测结果对样本进行加权，所以随着迭代不不断进行行，误差会越来越小，所以模型的偏差会不不断降低。这种算法无法并行。

2. CART回归树

CART回归树的关键师选取（s，j）；s是某个特征，j是划分点

CART就是递归的把所有的数据集划分为N个域，然后取每个域中的平均值作为当前叶节点的输出。选择哪个（s，j）对来作为当前结点中数据的的分裂依据是根据按照选定的（s，j）划分后，损失函数是不是最小。

3. Bagging算法：随机森林

随机森林本质上就是利用数据集训练多颗决策树。在预测的时候利用所有决策树中的众数来作为随机森林最后的输出。

随机森林算法

采取有放回的方法利用原来的数据集构建N个数据集，并利用这个N个数据集训练N颗决策树
当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
按照以上过程构建大量的决策树组成随机森林。

4. boosting算法：提升树

提升树是boosting算法的一种，本质上可以理解为是一个加法模型，他的基分类器是回归树模型。他的损失函数是均方误差损失函数，从公式的推到中可以看出。提升树的本质就是拟合残差。

提升树算法

$f_m(x) = f_{m-1}(x) + T(x;\theta_{m})$

$\hat{\theta}_{m} = argmin\sum{^N_{i=1}}(y_i, f_{m-1}(x_i)+T(x_i;\theta_{m}))$

当采用均方误差损失函数的时候，其loss函数变为：

$L(y,f_{m-1}(x)+T(x;\theta_{m}))\\=[y-f_{m-1}(x)-T(x;\theta_{m})]^2\\=[\gamma-T(x;\theta_{m})]$

其中 $f_{m-1}(x)$ 是之前得到的树的预测值； $\gamma$ 是残差（残差就可以使用回归树来拟合）；

5. boosting算法：Adaboost

Adaboost是一种自适应boosting算法，他的自适应体现在每训练完一个分类器，他会根据训练结果更新当前的数据集的权重。增大被错误分类的数据的权重，减少被正确分类的数据，然后利用更新以后的数据再次训练一个弱分类器并加入到之前得到的强分类器里。如此循环训练直到错误率达到某一个比较的值或者最大的迭代次数。

5.1 整个Adaboost 迭代算法就3步：

初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N。
训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

5.2 Adaboost算法流程

给定一个训练数据集T={(x1,y1), (x2,y2)…(xN,yN)}，yi属于标记集合{-1,+1}，Adaboost的目的就是从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。

步骤1. 首先，初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权值：1/N。

步骤2. 进行多轮迭代，用m = 1,2, …, M表示迭代的第多少轮
a. 使用具有权值分布Dm的训练数据集学习，得到基本分类器（选取让误差率最低的阈值来设计基本分类器）：

b. 计算Gm(x)在训练数据集上的分类误差率

由上述式子可知，Gm(x)在训练数据集上的误差率em就是被Gm(x)误分类样本的权值之和。

c. 计算Gm(x)的系数，am表示Gm(x)在最终分类器中的重要程度（目的：得到基本分类器在最终分类器中所占的权重。注：这个公式写成 $\alpha_m=1/2ln((1-e_m)/e_m)$ 更准确，因为底数是自然对数e，故用In，写成log容易让人误以为底数是2或别的底数，下同）：

由上述式子可知， $e_m <= 1/2$ 时， $\alpha_m >= 0$ ，且 $\alpha_m$ 随着 $e_m$ 的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。

d. 更新训练数据集的权值分布（目的：得到样本的新的权值分布），用于下一轮迭代

使得被基本分类器Gm(x)误分类样本的权值增大，而被正确分类样本的权值减小。就这样，通过这样的方式，AdaBoost方法能“重点关注”或“聚焦于”那些较难分的样本上。

其中，Zm是规范化因子，使得Dm+1成为一个概率分布：

步骤3. 组合各个弱分类器

从而得到最终分类器，如下：

6. boosting算法：GBDT

GBDT应该和提升树联系在一起。提升树的损失函数是均方误差损失函数，此时就相当于利用一颗回归树来拟合当前数据的残差，但是当损失函数不再是均方误差的时候，提升树就显得无能为力了。因此为了扩展到其他损失函数上，提出了GBDT算法。当GBDT算法采用均方损失的时候，GBDT和提升树就很接近了。GBDT是借鉴于梯度下降法，其基本原理是根据当前模型损失函数的负梯度信息来训练新加入的弱分类器，然后将训练好的弱分类器以累加的形式结合到现有模型中，他的基分类器是采用回归树。

GBDT拓展到用弱分类器来拟合负梯度主要是利用了一阶泰勒展开式来看，从泰勒展开式的第二项看，如果要使得损失函数下降，只需要使得要训练的基分类器的输出在数值上等于损失函数在当前点的负值就可以。也就是利用基分类器去拟合负梯度。

6.1 GBDT拟合的为什么是负梯度

优化目标函数： $\sum{_{i=1}^N}L(y_{i},h_{m-1}(x_{i})+f_{m}(x_{i}))$
最小化上述目标函数，也就是每添加一个弱分类器就使得损失函数下降一部分。利用泰勒公式对上述问题进行近似来回答为什么GBDT拟合的是负梯度
$L(y_{i},h_{m-1}(x_{i})+f_{m}(x_{i})) = \\L(y_{i},h_{m-1}(x_{i}))+ \frac{\partial{L(y_{i},f_{m-1}(x_{i}))}}{\partial(f_{m-1}(x))}*f_{m}(x_{i})$
当
$f_{m}(x_{i}) = -\frac{\partial{L(y_{i},f_{m-1}(x_{i}))}}{\partial(f_{m-1}(x))}$ 则肯定有 $L(y_{i},h_{m-1}(x_{i})+f_{m}(x_{i})) L(yi,hm−1(xi)+fm(xi))<L(yi,hm−1(xi))$

6.2 在GBDT种如何确定当前的点是否要分裂的依据

我们可以把损失函数由每个样本的表达形式转化为每个叶节点表达的形式，由此可以计算出该叶节点分裂前后的损失函数减少值，如果该值的减少符合预期就对当前结点进行分裂，否则就不分裂。

6.3 QA

Q1. GBDT为什么是拟合负梯度
GBDT本身就是一个回归算法，回归算法的本质就是最小化损失函数，而最小化损失函数的本质又是梯度下降。这里采用平方差和作为损失函数，其求导正好是残差，所以就相当于是利用提升树来集合残差。

Q2. 在GBDT中为什么使用泰勒公式推导梯度下降算法
泰勒公式推导只是一种方法

Q3. GBDT和提升树区别
提升树模型每一次的提升都是靠上次的预测结果与训练数据的label值差值作为新的训练数据进行重新训练，由于原始的回归树指定了平方损失函数所以可以直接计算残差，而梯度提升树针对一般损失函数，所以采用负梯度来近似求解残差，将残差计算替换成了损失函数的梯度方向，将上一次的预测结果带入梯度中求出本轮的训练数据。这两种模型就是在生成新的训练数据时采用了不同的方法。

Q4. GBDT是如何防止过拟合的

为了防止过拟合，在GBDT中用到了Shrinkage–缩减，循序渐进：Shrinkage的思想强调的是循序渐进，就好比不能一口吃出一个胖子。每次迭代只走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。在参考博文一中使用了这个技巧。也就是最后的强学习构造中给予了后面学到的每棵树一个权重。 $f_{M}(x) = f_{0}(x) + lr*\sum{_{i=1}^M}\sum{_{j=1}^N}T(x,\theta)$
控制迭代的次数，也就是控制生成的树的数量
控制叶子节点中最少的样本个数
控制树的复杂性

Q5. GBDT是如何实现正则化的

第一种是和Adaboost类似的正则化项，即步长(learning rate)。也就是shrinkage来确定每一步学到的知识的多少
第二种正则化的方式是通过子采样比例（subsample）。取值为(0,1]
第三种是对于弱学习器即CART回归树进行正则化剪枝

Q6. GBDT的优缺点
　　GBDT主要的优点有：
　　1) 可以灵活处理各种类型的数据，包括连续值和离散值。
　　2) 在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。
3）使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
　　GBDT的主要缺点有：
　　1)由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

7. boosting算法：XGBoost

Python机器学习笔记：XgBoost算法

XGBoost和GBDT的不同

XGBoost的详细公式推导

目前看到的对XGBoost最好的解读

20道XGBoost面试题

7.1 XGBoost和GBDT介绍

XGboost和GBDT是boosting算法的一种，XGBoost其本质上还是一个GBDT的工程实现，但是力争把速度和效率发挥到极致。

GBDT算法本身也是一种加法模型，是对提升树一种优化。他使得boosting算法可以拓展到应对任何损失函数类别。理论中，针对GBDT的损失函数做了一个一阶泰勒近似，一阶泰勒近似的结果就是一个一阶导数，也就是梯度。因此本质上GBDT是对损失函数的负梯度的一个拟合，当损失函数采用均方误差损失的时候，GBDT拟合的负梯度就是残差。在这个过程中，GBDT使用的基分类器是CART回归树。

对于XGBoost，是GBDT的一种优化。但是相对GBDT， XGBoot主要在以下几个方面做了优化:

XGBoost是GBDT的一种工程实现方式，在GBDT的理论推导中，是利用一阶泰勒近似得到了GBDT本质上就是拟合损失函数的负梯度，但是XGBoot是利用到了一阶和二阶信息。二阶信息保证了模型训练的更准确收敛的更快。
GBDT中只是利用回归树来作为他的基分类器，但是XGBoost中还添加了线性分类器。并且在XGBoost的目标函数中添加了正则项来约束最后学习到的模型。
XGBoost在训练的过程中支持列抽样，类似于随机森林可以选择部分特征。这样不仅可以减少过拟合的风险还可以减少计算量。
XGBoot是支持并行的，这也是最主要优于GBDT的一点。XGBoost的并行并不是体现在tree的粒度上，而是体现在特征的粒度上。决策树学习最耗时的一个步骤就是对特征的排序，因为要确定最佳的分割点。但是XGBoost在训练之前预先对数据进行排序，然后保存为block结构，后面的迭代中重复使用这个结构，这就大大减少了计算量。在进行节点的分裂时，要计算每个特征的增益，最后选择大的增益去做分类，那么这里就可以开多线程来进行特征的增益计算。
对于缺失样本，XGBoot可以自动学习出他的裂变方向。缺失值数据会被分到左子树和右子树分别计算损失，选择较优的那一个。如果训练中没有数据缺失，预测时出现了数据缺失，那么默认被分类到右子树。
可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。

为什么要使用二阶导数信息：二阶信息本身就能让梯度收敛更快更准确

7.2 XGBoost优化目标和公式推导

目标函数

其中正则项控制着模型的复杂度，包括了叶子节点数目T和leaf score的L2模的平方：

7.3 XGBoost防止过拟合的方法

引入正则化
在结点分裂时，采用类似于随机森林的列抽样
直接控制参数的复杂度，包括max_depth、min_child_weight gamma
add randomness来使得对训练对噪声鲁棒。包括subsample colsample_bytree。或者也可以减小步长 eta，但是需要增加num_round，来平衡步长因子的减小。
early stop等

7.4 XGBoost的特征重要性的计算

XGBoost根据增益情况计算出来选择哪个特征作为分割点,而某个特征的重要性就是它在所有树中出现的次数之和。

7.5 XGBoost的特征并行化是怎么做的

决策树的学习最耗时的一个步骤就是对特征值进行排序,在进行节点分裂时需要计算每个特征的增益,最终选增益大的特征做分裂,各个特征的增益计算可开启多线程进行。而且可以采用并行化的近似直方图算法进行节点分裂。

7.6 XGB和LGB的区别

只想到三点，特征排序，特征切分和直方图和全排序

1）更快的训练速度和更高的效率：LightGBM使用基于直方图的算法。

2）直方图做差加速：一个子节点的直方图可以通过父节点的直方图减去兄弟节点的直方图得到，从而加速计算。

3）更低的内存占用：使用离散的箱子(bins)保存并替换连续值导致更少的内存占用。

4）更高的准确率(相比于其他任何提升算法)：它通过leaf-wise分裂方法（在当前所有叶子节点中选择分裂收益最大的节点进行分裂，如此递归进行，很明显leaf-wise这种做法容易过拟合，因为容易陷入比较高的深度中，因此需要对最大深度做限制，从而避免过拟合。）产生比level-wise分裂方法（对每一层所有节点做无差别分裂，可能有些节点的增益非常小，对结果影响不大，但是xgboost也进行了分裂，带来了务必要的开销）更复杂的树，这就是实现更高准确率的主要因素。然而，它有时候或导致过拟合，但是我们可以通过设置|max-depth|参数来防止过拟合的发生。

5）大数据处理能力：相比于XGBoost，由于它在训练时间上的缩减，它同样能够具有处理大数据的能力。

6）支持并行学习。

7）局部采样：对梯度大的样本（误差大）保留，对梯度小的样本进行采样，从而使得样本数量降低，提高运算速度。

7.7 XGB的缺点

XGBoosting采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低。
XGBoosting采用level-wise生成决策树，同时分裂同一层的叶子，从而进行多线程优化，不容易过拟合，但很多叶子节点的分裂增益较低，没必要进行跟进一步的分裂，这就带来了不必要的开销；LightGBM采用深度优化，leaf-wise生长策略，每次从当前叶子中选择增益最大的结点进行分裂，循环迭代，但会生长出更深的决策树，产生过拟合，因此引入了一个阈值进行限制，防止过拟合。

8. 各个集成学习算法之间的区别

8.1 GBDT和提升树的区别

这两种模型就是在生成新的训练数据时采用了不同的方法。**对于梯度提升树，其学习流程与提升树类似只是不再使用残差作为新的训练数据而是使用损失函数的梯度作为新的新的训练数据的y值。**但是如果GBDT采用平方损失作为损失函数，其梯度就又是残差。

8.2 Adaboost和GBDT的区别

Adaboost在每迭代一次以后，会对数据的权重做更新，被分错的数据会增大其权重，分对的数据会减少其权重；GBDT不会改变数据集的权重。
Adaboost会对每个分类器添加一个权重，同样GBDT也可以给每个弱分类器添加一个权重。他们的添加权重的目的是不一样的。Adaboost的权重在训练过程种更新来标定每个训练器的重要性。但是GBDT是为了防止过拟合，同时也是减少其学习率，使得学习的结果变的更加可靠。
Adaboost是通过更新数据集的权重来迭代的训练基分类器；但是对于GBDT，当其误差是均方误差的时候，他每次拟合的就是残差，也就是利用残差来更新数据集，当其损失函数是其他的损失的时候，每一个弱分类器拟合的就是损失函数的负梯度。

8.3 XGBoost和GBDT的区别

XGBoost是GBDT的一种工程实现方式，在GBDT的理论推导中，是利用一阶泰勒近似得到了GBDT本质上就是拟合损失函数的负梯度，但是XGBoot是利用到了一阶和二阶信息。二阶信息保证了模型训练的更准确收敛的更快。
GBDT中只是利用回归树来作为他的基分类器，但是XGBoost中还添加了线性分类器。并且在XGBoost的目标函数中添加了正则项来约束最后学习到的模型。
XGBoost在训练的过程中支持列抽样，类似于随机森林可以选择部分特征。这样不仅可以减少过拟合的风险还可以减少计算量。
XGBoot是支持并行的，这也是最主要优于GBDT的一点。XGBoost的并行并不是体现在tree的粒度上，而是体现在特征的粒度上。决策树学习最耗时的一个步骤就是对特征的排序，因为要确定最佳的分割点。但是XGBoost在训练之前预先对数据进行排序，然后保存为block结构，后面的迭代中重复使用这个结构，这就大大减少了计算量。在进行节点的分裂时，要计算每个特征的增益，最后选择大的增益去做分类，那么这里就可以开多线程来进行特征的增益计算。
对于缺失样本，XGBoot可以自动学习出他的裂变方向。缺失值数据会被分到左子树和右子树分别计算损失，选择较优的那一个。如果训练中没有数据缺失，预测时出现了数据缺失，那么默认被分类到右子树。
可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。

8.4 Adaboost和随机森林的区别

Adaboost是boosting算法，随机森林是bagging算法
Adaboost是每次调整训练集中样本点的权重来训练下一个分类器，但是随机森林是又放回的抽取N个数据集来组成新的训练集来训练弱分类器
Adaboost中每个弱分类器是有权重的，但是随机森林的各个分类器的权重是一样的，最后采取投票的方式得到最后的额结果
Adaboost的各个弱分类器是串行训练的，但是随机森林可以并行训练
随机森林是支持列抽样的。

8.5 GBDT和随机森林的区别

1）随机森林采用的bagging思想，而GBDT采用的boosting思想。

2）组成随机森林的树可以是分类树，也可以是回归树；而GBDT只由回归树组成。

3）组成随机森林的树可以并行生成；而GBDT只能是串行生成。

4）对于最终的输出结果，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来。

5）随机森林对异常值不敏感；GBDT对异常值非常敏感。

6）随机森林是通过减少模型方差提高性能；GBDT是通过减少模型偏差提高性能。

9. 关于集成学习的面试题集锦

1. bagging和boosting的区别

2. XGBoost和GBDT的区别

3. GBDT的原理和常用调参参数

先用一个初始值去学习一棵树,然后在叶子处得到预测值以及预测后的残差,之后的树则基于之前树的残差不断的拟合得到，从而训练出一系列的树作为模型。

n_estimators基学习器的最大迭代次数，learning_rate学习率，max_lead_nodes最大叶子节点数,max_depth树的最大深度,min_samples_leaf叶子节点上最少样本数。

GBDT中的小trick：

GBDT中采用shrinkage来设置步长，这样可以有效避免过拟合。

GBDT适用场景

GBDT几乎可用于所有回归问题（线性/非线性），GBDT的适用面非常广。亦可用于二分类问题（设定阈值，大于阈值为正例，反之为负例）。

10. SVM

**10.1 什么是SVM？**SVM和LR有什么区别

**支持向量机为一个二分类模型,它的基本模型定义为特征空间上的间隔最大的线性分类器。而它的学习策略为最大化分类间隔, 最终可转化为凸二次规划问题求解。**SVM中引入核函数的本质就是针对线性不可分的数据集，寻求一种可以在低纬度进行特征计算然后映射到高纬度进行分类的方法。但是其本质还是针对线性不可分的数据集，映射到高纬度后寻求一个空间几何平面对其进行分割。

SVM和LR的区别

LR是参数模型,SVM为非参数模型。（这里的参数和非参数指的是是否服从某个参数分布，而非模型中的参数）
LR采用的损失函数为logistical loss，而SVM采用的是hinge loss。
在学习分类器的时候, SVM利用其对偶性对原有目标函数进行转化，原有模型的复杂度和样本的维度有关，但是在转化后只是考虑与分类最相关的少数支持向量点。LR的模型相对简单, 在进行大规模线性分类时比较方便。

LR为什么不使用核函数：因为在SVM中核函数的本质是只计算支持向量，但是LR中会考虑所有的点，所有点都要两两计算，计算量太过庞大。

10.2 SVM中什么时候用线性核什么时候用高斯核?

当数据的特征提取的较好,所包含的信息量足够大,很多问题是线性可分的那么可以采用线性核。
若特征数较少,样本数适中,对于时间不敏感,遇到的问题是线性不可分的时候可以使用高斯核来达到更好的效果。

10.3 SVM中的软间隔和硬间隔

软间隔和硬间隔的差别就是有没有引入松弛变量

10.4 SVM中为什么要引入对偶问题

一是方便核函数的引入；
二是原问题的求解复杂度与特征的维数相关，而转成对偶问题后只支持向量的个数有关。

由于SVM的变量个数为支持向量的个数，相较于特征位数较少，因此转为对偶问题。通过拉格朗日算子法使带约束的优化目标转为不带约束的优化函数，使得W和b的偏导数等于零，带入原来的式子，再通过转成对偶问题。

10.5 核函数的种类和适用情形（这个回答是有错误的）

线性核、多项式核、高斯核

线性核：样本数量多且维度高；样本数量很多
高斯核：样本数量较少且维数不是很高，对时间不敏感

为什么高斯核可以映射无穷维度：因为把泰勒公式带入高斯核函数将得到一个无穷维度的映射

10.6 SVM的损失函数

合页损失函数

11. L1正则化和L2正则化

L1是模型各个参数的绝对值之和,L2为各个参数平方和的开方值。
L1更趋向于产生少量的特征,其它特征为0,最优的参数值很大概率出现在坐标轴上,从而导致产生稀疏的权重矩阵；而L2会选择更多的矩阵，但是这些矩阵趋向于0。

为什么一般利用L2解决过拟合问题而非L1

因为L1是一个绝对值求和的过程，在反向传播的过程中会涉及到求导，置零，解方程。但是如果给出一个绝对值方程，上述三者就会失效，求最小值就会有很大的麻烦

同样的对于 L1 和 L2 损失函数的选择，也会碰到同样的问题，所以最后大家一般用 L2 损失函数而不用 L1 损失函数的原因就是：因为计算方便！可以直接求导获得取最小值时各个参数的取值。此外还有一点，用 L2 一定只有一条最好的预测线，L1 则因为其性质可能存在多个最优解。当然 L1 损失函数主要就是鲁棒性 (Robust) 更强，对异常值更不敏感。

L1和L2的差别，为什么一个让绝对值最小，一个让平方最小，会有那么大的差别呢？看导数一个是1一个是w便知, 在靠进零附近, L1以匀速下降到零, 而L2则完全停下来了. 这说明L1是将不重要的特征(或者说, 重要性不在一个数量级上)尽快剔除, L2则是把特征贡献尽量压缩最小但不至于为零.

L2平方项是个圆圈，防止过拟合找到最优化，L1是个正方形歪放在坐标轴，选出少量特征。

12. 降维（PCA）

PCA是比较常见的线性降维方法,通过线性投影将高维数据映射到低维数据中,所期望的是在投影的维度上,新特征自身的方差尽量大,方差越大特征越有效,尽量使产生的新特征间的相关性越小。

PCA算法的具体操作为对所有的样本进行中心化操作,计算样本的协方差矩阵,然后对协方差矩阵做特征值分解,取最大的n个特征值对应的特征向量构造投影矩阵。

13. K-means

从数据集中随机选择k个聚类样本作为初始的聚类中心,然后计算数据集中每个样本到这k个聚类中心的距离,并将此样本分到距离最小的聚类中心所对应的类中。
将所有样本归类后,对于每个类别重新计算每个类别的聚类中心即每个类中所有样本的质心,重复以上操作直到聚类中心不变为止。

14. 机器学习中的训练trick问题

14.1 如何防止过拟合

L1和L2正则化
dropout
提前停止
数据集扩增
简化网络结构
使用boosting或者bagging方法

14.2 梯度消失和梯度爆炸

9. 梯度消失梯度爆炸原因与解决方式

梯度消失和梯度爆炸

概念和表现：在反向求导的过程中，前面每层的梯度都是来自后面每层梯度的乘积，当层数过多时，有可能产生梯度不稳定，也就是梯度消失或者梯度爆炸，他门的本质都是因为梯度反向传播中的连乘效应。他的表现就是随着网络层数的加深，但是模型的效果却降低了。

梯度消失产生的原因： 隐藏层数量太大，使用了不合适的激活函数

**梯度爆炸产生的原因：**隐藏层数量太大，权重的初始化值过大，使用了不合适的激活函数

如何解决：

预训练加微调
加入正则化
梯度修剪
选择合适的激活函数，relu、leakrelu、elu等激活函数
batchnorm

Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization，简称BN，即批规范化，通过规范化操作把数据拉回到激活函数的梯度敏感区域，使得模型有一个更易于收敛。
LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，如下图，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。
减少网络隐藏层的数量
选择合适的初始化手段

为什么ReLU可以避免梯度消失的问题

ReLU的正半轴是线性的，他的导数是1且是一个固定值，所以容易避免发生梯度消失和梯度爆炸的问题。但是他并不能从根本上解决梯度消失的问题，因为当输入是小于0的时候，就会把Relu的负半轴激活，在这一侧，ReLU的输出就是0，导数也是0，他依旧无法避免梯度消失的问题。

为什么选用ReLu而不是sigmoid，因为sigmoid只在0的附近具有比较好的特性，随着数据的增大结合减小，梯度就会趋近于0，进而产生梯度消失的现象。但是Relu在大于0的区间导数是一个常数，不存在梯度消失或者梯度爆炸的问题，并且他使得模型的训练速度更快，更容易收敛。

14.3 在分类任务上使用交叉熵而非均方误差的原因主要是：

分类任务上常用的激活函数是sigmoid，如果使用均方误差的话，在使用梯度下降算法更新时，权值w的偏导会含有sigmoid函数导数项(在输出接近0和1时会非常小)，导致训练阶段学习速度会变得很慢，而如果用交叉熵的话，求权值w的偏导时不含sigmoid函数的导数项的，所以不会出现这个问题。所以在分类任务上，我们一般使用交叉熵。

14.4 可以问LR为什么用交叉熵不用均方误差

mse会梯度消失且非凸，容易找到局部最小

14.5 数据增强

在自然语言处理领域，被验证为有效的数据增强算法相对要少很多，下面我们介绍几种常见方法。

同义词词典（Thesaurus）：Zhang Xiang等人提出了Character-level Convolutional Networks for Text Classification，通过实验，他们发现可以将单词替换为它的同义词进行数据增强，这种同义词替换的方法可以在很短的时间内生成大量的数据。
随机插入（Randomly Insert）：随机选择一个单词，选择它的一个同义词，插入原句子中的随机位置，举一个例子：“我爱中国” —> “喜欢我爱中国”。
随机交换（Randomly Swap）：随机选择一对单词，交换位置。
随机删除（Randomly Delete）：随机删除句子中的单词。
加噪（NoiseMix） (https://github.com/noisemix/noisemix)：类似于图像领域的加噪，NoiseMix提供9种单词级别和2种句子级别的扰动来生成更多的句子，例如：这是一本很棒的书，但是他们的运送太慢了。->这是本很棒的书，但是运送太慢了。
情境增强（Contextual Augmentation）：这种数据增强算法是用于文本分类任务的独立于域的数据扩充。通过用标签条件的双向语言模型预测的其他单词替换单词，可以增强监督数据集中的文本。
回译技术（Back Translation）：回译技术是NLP在机器翻译中经常使用的一个数据增强的方法。其本质就是快速产生一些翻译结果达到增加数据的目的。回译的方法可以增加文本数据的多样性，相比替换词来说，有时可以改变句法结构等，并保留语义信息。但是，回译的方法产生的数据严重依赖于翻译的质量。
扩句-缩句-句法：先将句子压缩，得到句子的缩写，然后再扩写，通过这种方法生成的句子和原句子具有相似的结构，但是可能会带来语义信息的损失。
无监督数据扩增（Unsupervised Data Augmentation）：通常的数据增强算法都是为有监督任务服务，这个方法是针对无监督学习任务进行数据增强的算法，UDA方法生成无监督数据与原始无监督数据具备分布的一致性，而以前的方法通常只是应用高斯噪声和Dropout噪声（无法保证一致性）。(https://arxiv.org/abs/1904.12848)

14.6 数据不平衡怎么办

在损失函数计算时增加少数样本的权重
使用等批量的正负数据集构建多个小样本
上下采样

14.7 Batch Nomalization的作用

神经网络在训练的时候随着网络层数的加深,激活函数的输入值的整体分布逐渐往激活函数的取值区间上下限靠近,从而导致在反向传播时低层的神经网络的梯度消失。而BatchNormalization的作用是通过规范化的手段,将越来越偏的分布拉回到标准化的正态分布,使得激活函数的输入值落在激活函数对输入比较敏感的区域，从而使梯度变大，加快学习收敛速度，避免梯度消失的问题。

layer normalization应该放在激活函数的前面还是后面？

Pre-LN相较传统Transformer的Post-LN在训练阶段可以不需要warm-up并且模型更加稳定、收敛更快。(warm-up可以避免全连接层的不稳定的剧烈改变。在有了warm-up之后，模型能够学得更稳定)

BN和LN的区别

Batch Normalization 的处理对象是对一批样本， Layer Normalization 的处理对象是单个样本。

Batch Normalization 是对这批样本的同一维度特征做归一化， Layer Normalization 是对这单个样本的所有维度特征做归一化。

14.8 3*3的卷积核的好处

2个3*3的卷积核串联和5*5的卷积核有相同的感知野,前者拥有更少的参数。多个3*3的卷积核比一个较大尺寸的卷积核有更多层的非线性函数,增加了非线性表达,使判决函数更具有判决性。

14.9 Relu比sigmoid好在什么地方

sigmoid的导数只有在0的附近时有较好的激活性,而在正负饱和区域的梯度趋向于0,从而产生梯度消失的现象,而relu在大于0的部分梯度为常数,所以不会有梯度消失现象。
Relu的导数计算的更快。
Relu在负半区的导数为0,所以神经元激活值为负时,梯度为0,此神经元不参与训练,具有稀疏性。

14.10 什么是dropout

在神经网络的训练过程中,对于神经单元按一定的概率将其随机从网络中丢弃,从而达到对于每个mini-batch都是在训练不同网络的效果,防止过拟合。

14.11 dropConnect

防止过拟合方法的一种,与dropout不同的是,它不是按概率将隐藏层的节点输出清0,而是对每个节点与之相连的输入权值以一定的概率清0。

14.12 SGD, Adam等优化器

1）SGD；2）Momentum；3）Nesterov；4）Adagrad；5）Adadelta；6）RMSprop；7）Adam；8）Adamax；9）Nadam。
（1）对于稀疏数据，尽量使用学习率可自适应的算法，不用手动调节，而且最好采用默认参数。
（2）SGD通常训练时间最长，但是在好的初始化和学习率调度方案下，结果往往更可靠。但SGD容易困在鞍点，这个缺点也不能忽略。
（3）如果在意收敛的速度，并且需要训练比较深比较复杂的网络时，推荐使用学习率自适应的优化方
（4）Adagrad，Adadelta和RMSprop是比较相近的算法，表现都差不多。
（5）在能使用带动量的RMSprop或者Adam的地方，使用Nadam往往能取得更好的效果。

14.13 1*1卷积的作用

实现跨通道的信息交互整合,
降维和升维,
增加模型的非线性性,
可是实现与全连接层的等价效果

14.14 神经网络为什么使用交叉熵

通过神经网络解决多分类问题时，最常用的一种方式就是在最后一层设置n个输出节点，无论在浅层神经网络还是在CNN中都是如此，比如，在AlexNet中最后的输出层有1000个节点，而即便是ResNet取消了全连接层，也会在最后有一个1000个节点的输出层。

一般情况下，最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N，那么对于每一个样例，神经网络可以得到一个N维的数组作为输出结果，数组中每一个维度会对应一个类别。在最理想的情况下，如果一个样本属于k，那么这个类别所对应的的输出节点的输出值应该为1，而其他节点的输出都为0，即[0,0,1,0,….0,0]，这个数组也就是样本的Label，是神经网络最期望的输出结果，交叉熵就是用来判定实际的输出与期望的输出的接近程度。

14.15 梯度下降法如何跳出局部最小值

采用不同的初始化方式来初始化多个神经网络，然后进行训练。最后选择效果最好的神经网络的参数作为最佳的参数
采用随机梯度下降法。SGD由于每次参数更新仅仅需要计算一个样本的梯度，训练速度很快，即使在样本量很大的情况下，可能只需要其中一部分样本就能迭代到最优解，由于每次迭代并不是都向着整体最优化方向，导致梯度下降的波动非常大，更容易从一个局部最优跳到另一个局部最优，准确度下降。
使用模拟退火的方案。(这个是一个不熟悉的方案)

14.16各个优化器之间的区别

优化算法Optimizer比较和总结

14.17 反向传播的原理

https://www.zhihu.com/question/27239198

14.18 牛顿法的缺点

对目标函数有较严格的要求。函数必须具有连续的一、二阶偏导数，Hissen矩阵必须正定。
计算相当复杂，除需要计算梯度以外，还需要计算二阶偏导数矩阵和它的逆矩阵。计算量、存储量均很大，且均以维数N的平方增加，当N很大时这个问题更加突出。

14.19 句子分布不均衡如何解决

采用文本增强的方法进行解决

回译
EDA

14.20 L1不可导怎么办

使用坐标轴下降法进行优化

坐标下降法属于一种非梯度优化的方法，它在每步迭代中沿一个坐标的方向进行线性搜索（线性搜索是不需要求导数的），通过循环使用不同的坐标方法来达到目标函数的局部极小值。

14.21 查准率（Precision）和查全率（召回率Recall）

14.22 简单介绍一下ROC和AUC

我们得到混淆矩阵后，可以计算出 TPR 和 FPR ，然后用 FPR 做横轴，TPR 做纵轴，画出一条 FPR-TPR 曲线，就是 ROC 曲线，ROC 曲线下方的面积就是 AUC。我们计算 AUC 的时候可以根据定义取多个 threshold，用矩形的面积来拟合曲线下面积。但是在实际使用中，这种算法效率很低，因为对于每一个 threshold 都需要计算 TP、TN、FP、FN，实际过程中人们是使用 rank 来做。

六、概率问题

1. 最大似然估计和最大后验概率

最大似然估计提供了一种给定观察数据来评估模型参数的方法,而最大似然估计中的采样满足所有采样都是独立分布的假设。
最大后验概率是根据经验数据获难以观察量的点估计,与最大似然估计最大的不同是最大后验概率融入了要估计量的先验分布在其中,所以最大后验概率可以看做规则化的最大似然估计。

2. 概率和似然的区别

概率是指在给定参数 $\theta$ 的情况下,样本的随机向量X=x的可能性。而似然表示的是在给定样本X=x的情况下,参数 $\theta$ 为真实值的可能性。一般情况,对随机变量的取值用概率表示。而在非贝叶斯统计的情况下,参数为一个实数而不是随机变量,一般用似然来表示。

七、python相关

1. 基础概念

1.1 生成器和迭代器

生成器

python生成器是一个返回可以迭代对象的函数,可以被用作控制循环的迭代行为。生成器类似于返回值为数组的一个函数,这个函数可以接受参数,可以被调用,一般的函数会返回包括所有数值的数组,生成器一次只能返回一个值,这样消耗的内存将会大大减小。

1.2 is和==的区别

is用来判断连个变量引用的对象是否为同一个，==用于判断应用对象的值是否相等。

1.3 ctrl+c是挂掉程序而非抛出异常

1.4 dict和list的区别，dict的内部实验

dict查找速度快,占用的内存较大,list查找速度慢,占用内存较小,dict不能用来存储有序集合。Dict用{}表示,list用[]表示。

dict是通过hash表实现的,dict为一个数组,数组的索引键是通过hash函数处理后得到的,hash函数的目的是使键值均匀的分布在数组中。

1.5 python装饰器

装饰器的作用就是为已经存在的函数或对象添加额外的功能。

1.6 python多线程

Python代码的执行由Python虚拟机（解释器）来控制。Python在设计之初就考虑要在主循环中，同时只有一个线程在执行，就像单CPU的系统中运行多个进程那样，内存中可以存放多个程序，但任意时刻，只有一个程序在CPU中运行。同样地，虽然Python解释器可以运行多个线程，只有一个线程在解释器中运行。

1.7 python的垃圾回收机制

python中的垃圾回收机制是使用计数器实现的。

1.8 yiled和return的区别

return 是函数返回值，当执行到return，后续的逻辑代码不在执行

yield是创建迭代器，可以用for来遍历，有点事件触发的意思

#encoding:UTF-8  
def yield_test(n):  
    for i in range(n):  
        yield call(i) # 它会立即把call(i)输出，成果拿出来后才会进行下一步，所以 i, ',' 会先执行
        print("i=",i) # 后执行 #做一些其它的事情      
    print("do something.") #  待执行，最后才执行一遍
    print("end.")  
  
def call(i):  
    return i*2  
  
#使用for循环  
for i in yield_test(5):  
    print(i,",")   # 这里的 i 是 call(i)

1.9 python常用的string format

模板
%形式
format形式
f形式

import sys
from string import Template

a=10;
b=100
name="NEG"
t=Template("Hello $name!")
res=t.substitute(name=name)
print (res) # 模板
print("%d" %a) # %形式
print("{}".format(b)) # format形式
print(f"{a}") # f形式

八、NLP面经

1. 百度凤巢

1.rnn真的就梯度消失了吗？

RNN处理短序列文本的时候梯度并没有消失，但是处理长序列文本的时候，经过累乘结果会趋近于0，进而发生梯度消失。

2.lstm到底解决了什么？解决了梯度消失？

LSTM主要是通过门机制来缓解梯队消失的问题，尤其引入了遗忘门和输入门来对上一个状态进行选择性遗忘和对cell进行选择性更新，从宏观来看，他引入的cell也是贯穿整个网络的始终，前期的信息可以更好的保留到最后，很好的缓解了长依赖的问题。

3.gru结构和网络轻量化（减少参数）

2. vivo

1.LSTM三种门以及sigmoid函数对每个门的作用

LSTM的三个门主要包括遗忘门、输入门、输出门

遗忘门主要是通过sigmoid函数对上一层的隐藏层状态和 $h_{t-1}$ 和当前的 $x_t$ 进行计算得到遗忘因子，利用遗忘因子和上一层的cell进行相乘对上一层的cell部分信息进行遗忘
输入门也称为选择性记忆门，是对当前的输入信息 $x_t$ 进行选择性记忆。这部分的输出也会用来去更新经过遗忘门处理后的cell
输出门主要是考虑多少cell中的信息进入到当前的输出的隐藏层状态中。

sigmoid就是一个门控机制，可以说就是一个门。当sigmoid的输出为1时表示门全部打开，为0时表示全部关闭。在遗忘门中控制有多少 $h_{t-1}$ 的信息被加入到cell，在输入门中表示有多少 $x_t$ 中有多少信息被用来更新cell，在输出门中表示有多少cell中的信息被用来考虑组成当前结点的隐藏层状态输出。

2.Self-attention的Query，Key，Value分别是什么。乘积是什么和什么的Query和Key相乘

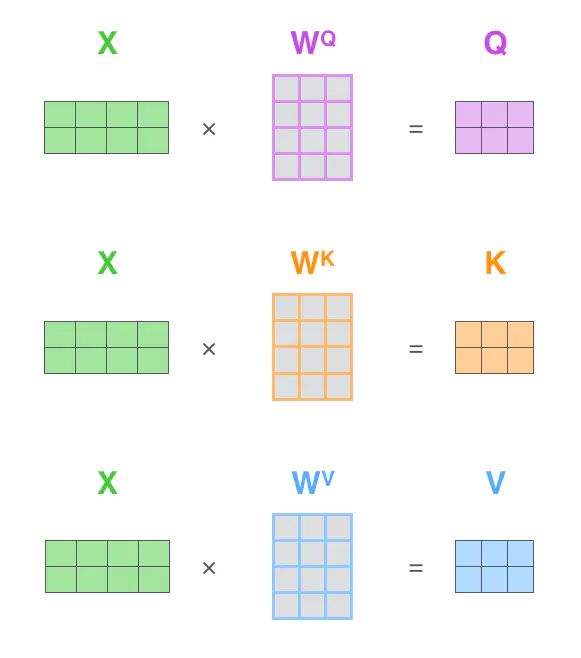
为什么要使用Q K V？ self-attention使用Q、K、V，这样三个参数矩阵独立，模型的表达能力和灵活性显然会比只用Q、V或者只用V要好些

Q K V是通过词嵌入乘以训练过程中创建的3个训练矩阵而产生的向量。这里面的训练矩阵是随机初始化的。

$softmax(\frac{Q\cdot K^T}{\sqrt{d_k}})\cdot V$

为什么要对self attention的q k v做一个线性变换？如果不对qkv进行变换的话，那么qkv三个矩阵应该是相同的，那么每个单词自己的q和k相乘的结果一定是最匹配最大的，这显然不是很科学

3. Self-attention的乘法计算和加法计算有什么区别？什么时候乘比较好，什么时候加

区别：

加法注意力使用了有一个隐藏层的前馈网络（全连接）来计算注意力分配
乘法注意力不用使用一个全连接层，所以空间复杂度占优；另外由于乘法可以使用优化的矩阵乘法运算，所以计算上也一般占优

论文中指出当 $d_{k}$ 比较小的时候，乘法注意力和加法注意力效果差不多；但当 $d_{k}$ 比较大的时候，如果不使用比例因子，则加法注意力要好一些，因为乘法结果会比较大，容易进入softmax函数的“饱和区”，梯度较小。

4. 为什么要除以一个根号？也是归一化

除以 $\sqrt d_{k}$ 是为了得到更平稳的梯度。因为随着 $d_k$ 的增大， $\cdot k$ 点积后的结果也随之增大，这样会将softmax函数推入梯度非常小的区域，使得收敛困难。因此对其做一个缩放，是为了得到更平稳的梯度，也有利于模型的收敛。

5. 多头注意力机制的原理是什么？

multi-head就是初始化多个 $W^Q, W^K, W^V$ 训练矩阵，针对同一个对象得到多个Q K V 表示向量，进而得到当前对象的多个表示方法，有利于提升得到的词向量表达信息的多样性和丰富性。同时也是让模型去关注不同方面的信息，最后再将各个方面的信息综合起来。

6. Transformer用的是哪种attention机制？

self-attention

7. bert的位置编码和transformer有什么不同

BERT是随机初始化的位置向量，Transformer是利用sin/cos位置函数得到的位置向量。由于BERT的参数量比较大并且训练的语料库也比较大，这两种位置编码在BERT的最后的训练过程中得到的效果都差不多，但是使用随机初始化更方便，并且节省计算时间。

8. bert为什么需要多头，为什么bert有12层encoder，如果是QA问题，你知道该如何调整encoder的层数吗？

BERT本身是使用的Transformer的encoder，也就使用了多头注意力机制。这是为了防止以当前处理对象为主导，使得self-attention得到的信息不完整，不丰富。使用多头的目的就是充分考虑序列当中处理对象与其他单词尽可能多的信息，使得得到的向量表达的信息更完善更丰富。

BERT的每个层得到信息是不一样的，越在下面的层学的更多的是语法和句法信息，越往上学得的信息越抽象越高级比如语义特征等。针对QA问题，我们应该增加层数，使用更高级得语义信息。

9. 去掉self-attention是否可以得到词向量

可以得到，因为还存在全连接层，所以还是可以拿到词向量。

10. 为什么要去掉停用词

停用词一般指使用非常广泛或者频率非常高的词。这类词一般会占用存储空间，并且对有效的信息造成干扰，也就是说本身是一个噪声，可能会造成其他重要信息得丢失。因此要对这类词去除。

11. word2vec为什么没有预训练，word2vec和bert的区别，和ELMO的区别

3. 京东

1.bert怎么分词？

BERT是如何分词的

2.为什么lstm门用tanh？

使用tanh只是一个实验的过程，并且lstm默认的也是tanh，但是当网络层加深后，LSTM依旧面临梯度消失的风险，这个时候还是要使用RELU激活函数来尽可能的避免梯度消失问题。

3. tensorflow与pytorch区别

4. 岭回归和lasso回归的区别

Lasso是加 L1 penalty，也就是绝对值；岭回归是加 L2 penalty，也就是二范数。
从贝叶斯角度看，L1 正则项等价于参数 w 的先验概率分布满足拉普拉斯分布，而 L2 正则项等价于参数 w 的先验概率分布满足高斯分布。
从优化求解来看，岭回归可以使用梯度为零求出闭式解，而 Lasso 由于存在绝对值，在 0 处不可导，只能使用 Proximal Mapping 迭代求最优解。
从结果上看，L1 正则项会使得权重比较稀疏，即存在许多 0 值；L2 正则项会使权重比较小，即存在很多接近 0 的值。

5. L1和L2正则化如何选择

L1正则化可以用来做特征选择，如果只是解决过拟合的问题， L1和L2都可以

6. 如果把激活函数全都换成线性函数，会出现什么问题
如果把激活函数全都换成线性函数会失去非线性性，退化为一个线性回归。如果是分类问题最后有一个 sigmoid 层，则退化为逻辑回归。深度学习能起作用的本质原因就是使用了非线性的激活函数，从而通过很多神经元可以拟合任意一个函数。

7. AUC的含义是什么

假设从所有正样本中随机选取一个样本，把该样本预测为正样本的概率为 p1，从所有负样本中随机选取一个样本，把该样本预测为正样本的概率为p0，p1 > p0 的概率就是 AUC。

4. OPPO

1. attention的实现

attention机制主要是用seq2seq模型中，再来encode中我们得到每一个输入对应的隐藏层状态，然后再decoder中比如我们当前的状态是 $s_{t-1}$ ，那么我们可以使用endoder中的 $h_t$ 和 $s_{t-1}$ 相乘再利用softmax对其进行处理，这就得到了我们说的attention中的权重，利用上述得到的权重去乘我们的 $h_t$ ，就为我们的输入都分配了一个权重来预测我们后续的 $s_t$ 。

5. 百度

1. CNN特性

CNN主要的特性包括：

局部链接：能够提取局部的特征
权值共享：大大减少了训练参数的数量，降低了训练难度
降维：CNN可以通过池化或者卷积strides实现降维
多层次结构：将低层次的局部特征组合成较高层次的特征，不同层级的特征可以对应不同任务

2. LSTM特性

LSTM主要通过一个cell单元解决的文本在时序上的一个长期依赖关系。LSTM的内部结构主要包括输入门，遗忘门门和输出门三个门结构。主要在遗忘门中，LSTM通过一个sigmoid函数来决定之前得到的隐藏层状态 $h_{t-1}$ 中有多少信息被遗忘。在后续中通过输入门决定cell中有什么信息需要保留或者说更新。

3. embedding模型

早期的包括one hot和词袋模型
固定的词向量模型包括：word2vec和glove
预训练模型包括ELMo、BERT、GPT等

4. RNN有哪些缺点? LSTM为什么比RNN好

RNN和LSTM的比较

RNN主要的缺点是存在梯度消失，无法解决长依赖问题。但是LSTM的门机制会对前期的信息是否需要保留做出一个判断，并且也会在输入门中来决定哪些信息需要被更新到cell当中。由于cell的存在，这就使得前期的有用信息会得到保留并延续到时间序列的最后，也就解决了长依赖问题。

遗忘门通过旧的状态 $h_{t-1}$ 和当前的输入 $x_{t}$ ，经有sigmoid函数来决定哪些信息需要被遗忘。
输入门通过旧的状态 $h_{t-1}$ 和当前的输入 $x_{t}$ ，经有sigmoid函数和tanh函数来决定哪些信息需要被保留，然后输入门的输出和遗忘门得到输出结合生成新的细胞状态 $c_t$ 。
最后输出门结合tanh和sigmoid函数来决定 $c_t, x_t,h_{t-1}$ 中的哪些信息组成新的 $h_t$ ；

LSTM的结构更加复杂，这也使得其不容易产生梯度消失。从宏观上来看，LSTM的各个单元之间有一个cell单元贯穿始终，这也就使得LSTM能解决长期依赖的问题。

5. BERT和ELMo比较

BERT的特征提取结构采用的是transformer的encoder，而ELMo采用的是LSTM，但是Transformer提取特征的能力更强
BERT的训练参数和训练的语料库要比ELMo大的多，这也使得BERT的效果比ELMo更强。
BERT的层数更多，在每个层得到的信息是不一样的，在使用的时候可以针对每个层的得到的信息来使用，但是ELMo就两层，一层关注语法信息，一层关注语义信息。从这里比较来看，BERT也更好。

6. BERT介绍/Transformer介绍

6.1 Transformer介绍
Transformer本身是一个encoder-decoder模型，那么也就可以从encoder和decoder两个方面介绍。

**对于encoder，**原文是由6个相同的大模块组成，每一个大模块内部又包含多头self-attention模块和前馈神经网络模块。尤其是对于多头self-attention模块相对与传统的attention机制能更关注输入序列中单词与单词之间的依赖关系，让输入序列的表达更加丰富。同时这里的encoder模块也是BERT的一个主要的组成模块。

6.2 BERT介绍
BERT其实是一个预训练模型。不同于ELMo中的双向LSTM，他的模型主要组成的内容就是transformer的encoder。此外GPT模型的主要组成模块也是Transformer的encoder，但是GPT只关注当前处理对象的上文，而BERT对transformer的使用不同于GPT而是类似于双向LSTM，利用当前处理对象的上下文信息处理当前的对象。

原文中提到的BERT主要有两种模型。一个是BERT base和BERT large。两者的主要区别是模型的深度和参数量的不同。对于BERT的预训练，原文是提出了两种训练方式，一种是mask language model，这种主要是低输入的token利用mask进行遮掩部分的token，训练BERT来预测被mask的单词。另一种训练方式是next sentence predction，这里主要是输入一个句子对，让BERT来预测这两个句子是否是真正的句子对。但是在实际的训练过程中，两者是一块进行的。

针对BERT的整个训练模型，BERT的低层次模型更倾向于语法特征的学习，高层偏向于语义特征的学习。

目前还出现了bert_as_sevice来直接使用BERT。以上就是对BERT的一个简单介绍。

7. 如何解决OOV问题

例如引入UNK，
所有的OOV词拆成字符(比如 Jessica，变成J，e，s，s，i，c，a)，
引入subwords(同样要进行拆词。不同的是，非OOV的词也要拆，并且非字符粒度，而是sub-word。还是 Jessica，变成Je，ssi，ca)，扩大词表。

8. PCA和softmax的差别

9. LSTM与GRU区别

GRU和LSTM的性能在很多任务上不分伯仲。
GRU 参数更少因此更容易收敛，但是数据集很大的情况下，LSTM表达性能更好。
从结构上来说，GRU只有两个门（update和reset），LSTM有三个门（forget，input，output），GRU直接将hidden state 传给下一个单元，而LSTM则用memory cell 把hidden state 包装起来。

10. batchsize大或小有什么问题

batch size过小，花费时间多，同时梯度震荡严重，不利于收敛；
batch size过大，不同batch的梯度方向没有任何变化，容易陷入局部极小值。

11. SVM和LR各自的应用场景

svm是对于已知的样本做超平面进行分类，所以他的功能偏重于所给的样本分类；逻辑回归是一种极大似然估计的方式，是想通过一直样本推断未知类别的分类。
如果说样本有限，需要预测的样本并不会很多，推荐svm；如果说样本有限，需要预测的样本趋近于无穷，那么推荐逻辑回归。
另外逻辑回归是基于二维空间的特征分类，多用于二分类，而svm可以通过kenerl trick技术升维以做到多分类。

12. 常用的模型评估指标

precision
recall
F1-score
PRC
ROC和AUC
IOU

6. 腾讯

1. 逻辑回归的损失函数

$-\sum{_{i=1}^N}[ y_ilog(h_{\theta}(x_i))+(1-y_i)log(1-h_{\theta}(x_i))]$

线性回归的损失函数是均方损失函数

2. 为什么逻辑回归为什么使用交叉熵损失不使用MSE

因为从反向求导来看，如果使用MSE，那么导数中就涉及sigmoid项，那么当输入很大或者很小的时候，梯度都不会改变，所以不考虑使用MSE，但是使用交叉熵损失等同于使用最大似然来学习一个由sigmoid参数化的Bernoulli分布。

3. SVM的损失函数是什么

合页损失函数

4. 核函数的种类

线性核函数：当数据量比较大，特征维度比较高（提取的信息比较充分）时使用线性核函数。
高斯核函数：当数据量适中，特征维度不是很高时使用高斯核函数
多项式核函数

5. 介绍BERT、Transformer、Attention的原理及其作用，要通俗的解释

先说明Transformer是什么，在说明利用Transformer的encoder组成了BERT的特征抽取单元，再说一下什么是Attention机制，得到权重的步骤，然后讲一下self-attention和传统attention机制的区别。

attention的算法步骤：（详细见上面的总结）

首先再encoder端得到所有输入的隐藏层状态。

在decoder端的当前隐藏层的状态是 $s_{t-1}$ ，我们使用 $s_{t-1}$ 和encoder端得到的状态相乘得到输出矩阵，然后使用softmax函数对其进行处理就得到了一个权重矩阵，我们把这个权重矩阵对隐藏层状态的 $h_t$ 进行加权求和，然后利用decoder端的 $s_{t-1}$ ，上一步的输出和当前的加权求和后的输出得到下一步的 $s_t$ 。

6. 基础编程语言

Python问题：

迭代器生成器差别
多线程有哪些函数
正则表达式match()和search()差别

7. word2vec的实现方式有哪些

CBOW（由上下文预测当前单词）相当于训练一次
skip-gram（由当前单词预测上下文）相当于要训练K次，因此skip-gram针对生词的训练更好，但是训练的速度慢

8. Dropout原理与作用

在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以防止过拟合，使模型泛化性更强。

为什么说Dropout可以解决过拟合？

（1）取平均的作用： 先回到标准的模型即没有dropout，我们用相同的训练数据去训练5个不同的神经网络，一般会得到5个不同的结果，此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9，其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合，取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络，随机删掉一半隐藏神经元导致网络结构已经不同，整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。

（2）减少神经元之间复杂的共适应关系： 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况。迫使网络去学习更加鲁棒的特征，这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测，它不应该对一些特定的线索片段太过敏感，即使丢失特定的线索，它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1，L2正则，减少权重使得网络对丢失特定神经元连接的鲁棒性提高。

（3）**Dropout类似于性别在生物进化中的角色：**物种为了生存往往会倾向于适应这种环境，环境突变则会导致物种难以做出及时反应，性别的出现可以繁衍出适应新环境的变种，有效的阻止过拟合，即避免环境改变时物种可能面临的灭绝。

总结：

dropout类似于一个取平均的过程，由于dropout是随机屏蔽一些神经网络，这就相当于再训练不同的网络，当一个网络出现过拟合，另外一个逻辑上的网络有可能会得到一个欠拟合的模型，这样取平均就可以得到更好的效果。

减少了神经元之间复杂的共适应关系：因为两个神经元不一定每次都在相同的网络下出现，这就阻止了某个特征在特定的情况下才有作用的条件。迫使神经元提高自己的鲁棒性

9. 梯度消失梯度爆炸原因与解决方式

梯度消失和梯度爆炸

梯度消失产生的原因： 隐藏层数量太大，使用了不合适的激活函数

**梯度爆炸产生的原因：**隐藏层数量太大，权重的初始化值过大，使用了不合适的激活函数

如何解决：

预训练加微调
加入正则化
梯度修剪
选择合适的激活函数，relu、leakrelu、elu等激活函数
batchnorm

Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization，简称BN，即批规范化，通过规范化操作把数据拉回到激活函数的梯度敏感区域，使得模型有一个更易于收敛。
LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，如下图，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。
减少网络隐藏层的数量
选择合适的初始化手段

为什么ReLU可以避免梯度消失的问题

ReLU的正半轴是线性的，他的导数是1且是一个固定值，所以容易避免发生梯度消失和梯度爆炸的问题。但是他并不能从根本上解决梯度消失的问题，因为当输入是小于0的时候，就会把Relu的负半轴激活，在这一侧，ReLU的输出就是0，导数也是0，他依旧无法避免梯度消失的问题。

10. 过拟合问题如何解决

定义：过拟合就是模型在训练集上表现很好，能对训练数据充分拟合，误差也很小，但是在训练集上表现很差，泛化性不好。

L1和L2正则化
dropout
提前停止
数据集扩增
简化网络结构
使用boosting或者bagging方法

11. word2vec是如何训练的

就是两种训练的方式 CBOW 和 skip-gram

12. 模型训练的停止标准是什么？如何确定模型的状态

停止的标准就是模型的指标不再上升，可以通过loss来观察模型的状态或者通过设置交叉验证集俩验证模型当前时刻的状态。

13. BERT细节，和GPT， ELMo的比较

BERT相对于GPT都是使用的Transformer的encoder端来作为网络内部的特征抽取器，但是GPT只是考虑了上文信息，类似于LSTM，但是BERT使用的上下问的饿信息，类似于BI-LSTM，对于ELMo，他内部使用的是LSTM来作为特征抽取器，并且ELMo相对于BERT的训练语料更少，参数量也更少。

14. Transformer结构，input_mask如何作用到后面self-attention计算过程

Transformer的encode中的层与层之间的链接是利用残差网路来进行连接的，因此输入可以直接作用于输出。呢么每个层之间都是使用残差来进行链接的，因此，input_mask就可以通过残差网络作用到后面的self-attention。

7. 字节跳动

1. bert 为什么scale product（为什么要除以 $\sqrt{d_k}$ ）

https://zhuanlan.zhihu.com/p/149634836

向量的点积结果会很大，将softmax函数push到梯度很小的区域，scaled会缓解这种现象

2. transformer里encoder的什么部分输入给decoder

Decoder和Encoder是类似的，如下图所示，区别在于它多了一个Encoder-Decoder Attention层，这个层的输入除了来自Self-Attention之外还有Encoder最后一层的所有时刻的输出。Encoder-Decoder Attention层的Query来自下一层，而Key和Value则来自Encoder的输出。

3. MLM 为什么mask一部分保留一部分

添加mask相当于添加噪声，那么当模型进行预测时，并不知道对应的输入位置是不是正确的单词，这就需要更多的依赖上下文的信息进行预测，增加了输入的随机性，也增加了模型的纠错能力。

做题

自己实现sqrt函数，结果保留5位小数
10亿个数，内存只有1M，如何让这10亿个数有序

利用桶排序

8.阿里

1. BERT里面的三种embedding分别是什么，为什么要这样做？

为什么BERT有三个嵌入层

三种编码：position embedding、segment Embeddings、token embedding
每个embedding的作用
- position embedding：通过让BERT在各个位置上学习一个向量表示来把序列顺序的信息编码进来。
- token embedding: 就是把各个词转换为固定维度的词向量
- segment embedding: 用来区分两个句子。BERT 能够处理对输入句子对的分类任务。这类任务就像判断两个文本是否是语义相似的。句子对中的两个句子被简单的拼接在一起后送入到模型中。那BERT如何去区分一个句子对中的两个句子呢？就是使用segment。

2. 如果要用树模型的话，可以做哪些特征工程？

n-gram，tf-idf，w2v

3. 假如说句子长度差别很大的话，tf-idf这个指标会有什么问题？one-hot encoding这个指标又会有什么问题

4. 介绍一下SVM，优化为什么要用对偶

支持向量机为一个二分类模型,它的基本模型定义为特征空间上的间隔最大的线性分类器。而它的学习策略为最大化分类间隔,最终可转化为凸二次规划问题求解。针对线性可分的问题，SVM并没有引入核函数，针对线性不可分的问题，SVM通过对偶性质引入和核函数来解决。这个时候SVM来进行分类的本质就是寻求一种使得可以在低纬度进行计算，但是相当于映射到高纬度上把不可分的数据集转换为可分的数据集。

引入对偶的目的主要是两个：

1）方便引入核函数；

2）原本模型的复杂度是和数据的维度有关，但是引入对偶问题以后，模型的复杂度只和变量的数量有关，这些变量就是支持向量。

5. Xgboost的应该着重调哪些参数

max_depth
min_child_weight
gamma
subsample
colsameple_bytree
正则化参数
减小学习率

6. 讲一下训练词向量的方法

word2vec
glove
ELMo
BERT

如何使用词向量生成句向量，可以是对每个句子的所有词向量取均值，来生成一个句子的vector

9. CVTE

1. 词袋模型有哪些不足的地方

稀疏，无序，纬度爆炸，不能表达语义上的差别，每个词都是正交的，相当于每个词都没有关系。

2. word2vec的两种优化方法

层softmax技巧（hierarchical softmax)
解释一：最后预测输出向量时候，大小是1*V 的向量，本质上是个多分类的问题。通过hierarchical softmax的技巧，把V分类的问题变成了log(V)次二分类。

负采样（negative sampling）
解释一：本质上是对训练集进行了采样，从而减小了训练集的大小。每个词的概率由下式决定：
$\frac{count(w)^{3/4}}{\sum\limits_{u \in vocab} count(u)^{3/4}}$

在训练每个样本时, 原始神经网络隐藏层权重的每次都会更新, 而负采样只挑选部分权重做小范围更新

解释三：

3. word2vec的优缺点

优点

由于 Word2vec 会考虑上下文，跟之前的 Embedding 方法相比，效果要更好（但不如 18 年之后的方法）
比之前的 Embedding方法维度更少，所以速度更快
通用性很强，可以用在各种 NLP 任务中

缺点

无法区分一词多义的问题
Word2vec 是一种静态的方式，虽然通用性强，但是无法针对特定任务做动态优化

4. lstm和rnn有什么区别，解决了什么问题，lstm计算上是如何计算的，lstm输出的维度是怎么样的

lstm和rnn的区别

对于RNN，他的内部实现比较简单，隐藏层状态的得到只是把上一时刻的状态和当前的输入做一个加权求和再包裹一层tanh激活函数，在短序列问题中能发挥比较好的作用，前面的词的信息可以很好的影响后面得到的隐藏层状态，但是由于序列的增加，可能回发生梯度消失的问题。
对于LSTM，他的内部是一系列门机制来实现的。主要是包括遗忘门，输入门，输出门。从宏观上来看，LSTM前后被一个cell state贯穿，前面的信息可以更好的影响到后面的决策过程。并且由于门机制的存在，他们的激活函数都是sigmoid激活函数，整个门的状态是是处于[0~1]之间的。当门为1时，梯度能够很好的在LSTM中传递，很大程度上减轻了梯度消失发生的概率，当门为0时，说明上一时刻的信息对当前时刻没有影响，我们也就没有必要传递梯度回去来更新参数了。

lstm的输出

他的输出就是一个 N*128 维的矩阵

10. 网易互娱

1. 如何对句子进行编码

对每个token的词向量进行相加然后去平均值

2. 提取句子的特征向量，有哪几种方式

CNN，LSTM，Attention

11. 拼多多

1. LSTM和CNN有什么区别，都适用什么场景

LSTM

LSTM的主要是为了解决RNN中的长依赖问题和梯度消失问题。他的实现主要是依靠门机制来实现。内部包括三个门：遗忘门，输入门，输出门。对于遗忘门，主要是依靠sigmoid函数来实现一个抽象的门的功能，当sigmoid的输出为0时，相当于关闭门，上一时刻的隐藏层状态信息会全部遗忘掉；当sigmoid的输出为1时，上一时刻的隐藏层状态信息会全部被用来更新cell状态。在输入门中通过sigmoid函数结合当前输入和上一时刻的状态输出来决定更新cell中的信息。从宏观上来看，LSTM中有一个cell单元贯穿始终，使得中间状态信息直接向后传播。因此这使得LSTM可以有效的解决长依赖问题。但是LSTM由于隐藏层状态的计算和上一时刻的状态有关，因此无法实现并行计算。

CNN

对于CNN，主要是由卷积层，池化层和全连接层来实现。原始的CNN，由于卷积核的限制，他也相当于处理一个N-gram问题，依旧无法解决长依赖的问题。但是随着Dilater CNN的出现，打破了原有的卷积核形式，可以使得卷积核可以以类似于跳一跳的形似提取前后文本序列的相关特征。但是由于CNN本身各个卷积核之间互不干扰，因此可以完美的实现并行计算。

2. xgboost 和 gbdt 区别 , gbdt 具体怎么实现的,具体讲一下,(比如说现在已经构建好了1 2 棵树那么第三棵树如何构建如何选择特征,具体说明)

区别

泰勒展开的一阶二阶信息
GBDT的基分类器只是回归树，但是XGB还加入了线性分类器。
XGB目标函数加入了正则
XGB再进行结点分裂时采用了RF中的列采样
XGB支持并行计算
对于缺失样本，XGBoot可以自动学习出他的裂变方向。缺失值数据会被分到左子树和右子树分别计算损失，选择较优的那一个。如果训练中没有数据缺失，预测时出现了数据缺失，那么默认被分类到右子树。
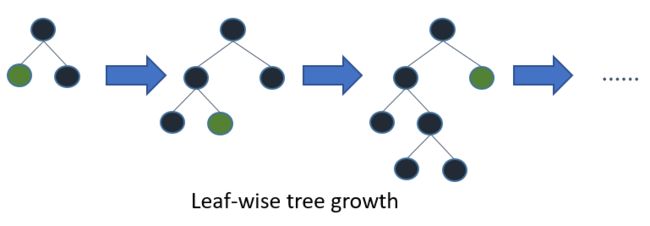
XGB引入了直方图(这个不是很理解)

GBDT的具体实现过程

已经构建了N颗树的时候，我们使用这N颗树的输出结果和原有数据集的label做差得到残差，这就是我们新的数据的label。也就是说假如我们原有数据集的特征是X，label是Y，那么现在对应每个X的Y就是我们得到的残差。
如何构建下一颗树？我们得到了新的数据集，那么依旧要选择最合适划分点，我们可以选择以当前所有特征作为划分特征，并选择该特征的每个取值作为阈值吧当前节点的饿左右数据划分为两个域，分别计算每个域的平局值作为输出，然后利用平方损失计算两个域对应的误差和。然后我们对所有的特征和所有的特征取值都重复这个过程，然后选择误差最小的特征和特征值作为划分的结点对结点数据进行划分。
当我们的树达到一定的深度，或者误差达到一定的值的时候不再继续分裂，这样我们就得到了第三个树。

3. cbow skipgram 具体说说区别, 负采样，层级softmax 原理具体说一下

cbow是利用上下文预测当前单词的方式来进行模型的训练，在训练的时候，会利用训练结果对当前N-gram中的单词进行调整
skip-gram是利用当前单词预测其对此那个的上下文。如果上下文包括K个单词，那么将会对当前单词的词向量调整K次。

4. 负采样

负采样主要是为了应对参数量太多，计算量太大的问题提出的一种解决方案。因为字典是非常大的，比如一万个，那么每次都需要对着一万个单词进行计算，那么反向传播的计算量是非常大的。但是我们可以只随机选择频率比较高的单词作为负样本进行反向传播，那么这个计算量就比较小了。

5. 层次softmax

这个主要是利用哈夫曼树的原理进行层次softmax。

12. 作业帮

1. GBDT和RF哪个树比较深

RF深。说了boost和bagging的思想。boost使用低方差学习器去拟合偏差，所以XBG和LGB有树深的参数设置，RF是拟合方差，对样本切对特征切，构造多样性样本集合，每棵树甚至不剪枝。

2. XGB是如何判断特征的重要性的

gain 增益意味着相应的特征对通过对模型中的每个树采取每个特征的贡献而计算出的模型的相对贡献。与其他特征相比，此度量值的较高值意味着它对于生成预测更为重要。
cover 覆盖度量指的是与此功能相关的观测的相对数量。例如，如果您有100个观察值，4个特征和3棵树，并且假设特征1分别用于决策树1，树2和树3中10个，5个和2个观察值的叶结点;那么该度量将计算此功能的覆盖范围为10+5+2 = 17个观测值。这将针对所有决策树结点进行计算，并将17个结点占总的百分比表示所有功能的覆盖指标。
**freq 频率（频率）**是表示特定特征在模型树中发生的相对次数的百分比。在上面的例子中，如果feature1发生在2个分裂中，1个分裂和3个分裂在每个树1，树2和树3中;那么特征1的权重将是2 1 3 = 6。特征1的频率被计算为其在所有特征的权重上的百分比权重。)

13. 蘑菇街

1. L1、L2不同？L1为什么能稀疏？

从数学分布讲了，L1是拉普拉斯分布， L2 是高斯分布；讲了图解为什么L1能稀疏，一个圈一个菱形，容易交在轴上。工程上讲了，L1的近似求导，区间内0区间外优化。然后L2是直接求导比较简单。

14. 携程

1. C4.5相对ID3决策树的优点

两者主要是结点分裂的计算标准不相同,ID3是使用的信息增益作为结点分类标准，而C4.5是使用信息增益比。

ID3算法以信息增益为准则来选择决策树划分属性。值多的属性更有可能会带来更高的纯度提升，所以信息增益的比较偏向选择取值多的属性。所以为了解决这个问题就用了信息增益比。C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

2. LSTM如何解决RNN存在的问题的？lstm的激活函数可以用relu吗？

理解RNN梯度消失和弥散以及LSTM为什么能解决

LSTM是如何解决梯度消失和梯度报站的问题的

RNN 存在梯度爆炸的根源

RNN的主要问题主要是在处理长距离信息的时候存在梯度消失或者梯度爆炸的问题，主要是由于在反向传播的过程中，导数小于1，累乘就会得到一个比较小的数，产生梯度消失。那么在反向传播的计算公式中还存在参数W，如果这个数值太大，经过梯度的累乘就会导致梯度爆炸的问题。

为什么不把RNN中的tanh激活函数换为ReLU？

ReLU可以在一定程度上缓解梯度消失的问题，但是有ReLU会导致非常大的输出，，最后的结果会变成多个W参数连乘，如果W中存在特征值>1，那么经过反向传播的连乘后就会产生梯度爆炸，RNN仍然无法传递较远的距离

RNN中的梯度消失和梯度爆炸

RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

LSTM解决梯度消失的本质方法

把返乡传播中的连乘变成了相加的形式，这就使得每一部分的梯度的权重相同，不容易产生梯度消失的问题，但是因为是相加，有可能会产生梯度爆炸的问题

RNN主要存在的问题是无法解决问题，并且存在梯度消失或者梯度爆炸的现象。产生这种现象的根源不主要是

15. 360

1. LSTM与RNN的区别

LSTM主要是结构上的不同，RNN和LSTM都可以把之前得到的隐藏层状态加入到当前隐藏层状态的生成中，但是

RNN内部是使用一个简单的加权求和并添加一层tanh激活函数来得到当前时刻的隐藏层状态，并且随着序列的加长，起始的隐藏层状态在后续中会产生较大的衰减，也就是无法应对长依赖问题，也容易发生梯度消失的问题。
LSTM的内部机制主要是三个门结构来决定之前隐藏层状态对当前时刻要生成的隐藏层状态的影响。并且从宏观上来看，LSTM前后有一个cell状态贯穿始终，能够比较好的解决长依赖的问题。

2. 梯度消失/爆炸的原因及解决方法

梯度消失产生的原因： 隐藏层数量太大，使用了不合适的激活函数

**梯度爆炸产生的原因：**隐藏层数量太大，权重的初始化值过大，使用了不合适的激活函数

如何解决：

预训练加微调
加入正则化
梯度修剪
选择合适的激活函数，relu、leakrelu、elu等激活函数
batchnorm

Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization，简称BN，即批规范化，通过规范化操作把数据拉回到激活函数的梯度敏感区域，使得模型有一个更易于收敛。
LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，如下图，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。
选择合适的权重初始化手段

为什么ReLU可以避免梯度消失的问题

ReLU的正半轴是线性的，他的导数是1且是一个固定值，所以容易避免发生梯度消失和梯度爆炸的问题。但是他并不能凶根本上解决梯度消失的问题，因为当输入是小于0的时候，就会把Relu的负半轴激活，在这一侧，ReLU的输出就是0，导数也是0，他依旧无法避免梯度消失的问题。

3. transform 的mask到底有什么作用

mask的作用相当于在输入侧引入噪声。在模型训练的过程中，模型并不知道输入的当前位置是否正确，那么久需要更多的依赖上下文去预测当前位置的正确性，一定程度上增加了训练数据的不确定性，另一方面也增加了模型的纠错能力。

4. lstm门到底那个门更新细胞状态

输入门对细胞状态进行更新（遗忘门的作用只是计算上一个状态的信息有多少在当前时刻得到保留并对此刻产生的隐藏层状态有多少影响）

5. 如何用word2vec的方式构造sentence2vec

得到每个单词的embedding，然后相加后取平均值作为当前的sentence2vec
直接concate作为当前句子的embedding
利用RNN对整个句子进行编码，直接取最后一个隐藏层状态作为当前句子的embedding
使用skip-gram的方式对句子进行训练，只不过把skip-gram中的单词换为句子向量

6. 数据归一化的好处

数据归一化后**，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解**。

7. 每次训练LSTM的权重是一样的吗？

参数是共享的，每一个时刻，用的都是同一个参数矩阵

8. 常见激活函数以及优缺点

sigmoid函数

优点：
1. Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。
2. 连续函数，便于求导。
缺点：
1. sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象，意味着函数会变得很平，并且对输入的微小改变会变得不敏感。在反向传播时，当梯度接近于0，权重基本不会更新，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
2. sigmoid函数的输出不是0均值的，会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。
3. 计算复杂度高，因为sigmoid函数是指数形式。
tanh函数

Tanh函数是 0 均值的，因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算的问题。
ReLU函数

优点：
1. 使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快。
2. 在x>0区域上，不会出现梯度饱和、梯度消失的问题。
3. 计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。
缺点：
1. ReLU的输出不是0均值的。
2. Dead ReLU Problem(神经元坏死现象)：ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。
产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

9. 数据不平衡怎么处理？

增加少数样本的权重
使用等批量的正负数据集构建多个小样本
上下采样

16. 海康威视

1. Transformer中涉及的几个公式写一下

1）multi-head attention层 $Attention(Z)=softmax(\frac{Q*K^T}{\sqrt{d_k}}*V)$
2）add&normal层 $L a y e r N o r m a l (x + S u b l a y e r (x))$
3）FFNN层 $FFNN(x)=max(0, xW_1+b_1)W_2+b_2$

17. 小米

1. encoder包含几个大块

multi-head attention模块
add&normal模块
FFNN模块

2. 马尔科夫决策过程

2.1 马尔科夫过程：

马尔可夫过程即为具有马尔可夫性的过程，即过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态都是独立、不相关的。

2.2 马尔科夫决策过程：

马尔可夫决策过程（Markov Decision Process，MDP）是带有决策的MRP，其可以由一个五元组构成。

S为有限的状态集合；
A为有限的动作集合；
P为状态转移矩阵；
R是奖赏函数；
γ为折扣因子（discount factor），其中 γ∈[0,1]γ∈[0,1]

我们讨论的MDP一般指有限（离散）马尔可夫决策过程。

1）策略

策略（Policy）是给定状态下的动作概率分布，即： $\pi(a|s)=P[A_t=a|S_t=a]$

3. 讲一下决策树

决策树就是if-else模型，他的主要步骤是寻找最优划分特征把当前节点分裂。那么针对每一个结点力的数据，如果采用的是ID3方法，那就计算他们的信息增益，选择最小的作为分类特征进行分裂，如果是C4.5就计算信息增益比来选择分裂的特征值。对于CART回归树是计算它的信息基尼系数来寻找最优的分裂特征和分裂特征值。

4. attention的计算过程

5. 随机森林的随机性体现在什么地方

数据是随机的，随机森林是基于bagging的算法，他才有有放回的方式随机生成一颗树的训练数据集
支持列抽样，选取的特征也是随机的

26个问串烧

1.如何解决过拟合问题，尽可能全面？（几乎每次都被问到）
定义：过拟合就是模型在训练集上表现很好，能对训练数据充分拟合，误差也很小，但是在训练集上表现很差，泛化性不好。
解决方案：

batchnarmal
训练提前停止
加L1,L2正则
扩大训练数据集
添加dropout

2.如何判断一个特征是否重要？

3.有效的特征工程有哪些？

方差选择法
相关系数法
卡方验证
互信息法
基于惩罚项的特征选择法
基于树模型的特征选择法

4.数学角度解释一下L1和L2正则化项的区别？

L1和L2的直观理解

直观的区别就是计算的方式不一样，L1正则就是在loss function后面加上模型参数的一范数，L2正则就是加上2范数。
L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

5.注意力机制，self-attention ？

传统注意力机制只是注重源序列和目标序列之间的关系，这里的建模更依靠的是源序列对目标序列的影响。
对于self-attention，他关注的更多是源序列和目标序列两个序列中单词与单词之间的一些关系。self-attention模型更倾向于捕捉源序列和目标序列自身的词依赖关系；然后再把源序列端的得到的self-attention加入到目标端的attention中去，捕捉他门之间的依赖关系.

6.有哪些embedding 方法？

one hot、词袋模型
word2vec、Glove
ELMo、BERT、GPT

7.word2vec中，为啥词义相近的两个词，embedding向量越靠近？

因为在word2vec的训练中，词义想接近的词，他们的使用方法和上下文也是接近的，那么得到的词向量就是比较接近的。

9.GBDT中的“梯度提升”，怎么理解？和“梯度下降”有啥异同？

在logistic的损失函数中，他本身是一个交叉熵损失函数，也就是求极大似然，那么就是利用梯度上升算法来求
在线性回归中，其损失函数是一个平方损失，要求其极小值，那么采用的就是梯度下降法来求。

10.常见的降维方法？PCA和神经网络的embedding降维有啥区别？

11.图卷积神经网络了解吗？（这里感谢滴滴面试官的提问，确实是我的盲点）

12.Bert为啥表现好？

训练的语料库大，模型更深，参数更多。并且Transformer提取特征的能力本身比LSTM等就强

13.SVM用折页损失函数有啥好处？

14.什么是交叉熵，为什么逻辑回归要用交叉熵作为损失函数？

为什么分类问题不适用均方误差，回归问题不适用交叉熵？

线性回归如果使用交叉熵损失函数，在训练的时候反向传播求导时的导数非常小，这将导致w，b的梯度不产生变化，也就是梯度消失现象，但是在使用平方误差时不会产生上述问题。

在分类问题中，我们希望模型学到的数据分布跟真实分布一致。但是我们无法得到真实分布，只能假设训练集的分布与真实的分布相近。我们希望模型尽可能拟合训练集的分布。衡量两个分布之间的不同一般用的是KL散度。最小化两个分布之间的不同相当于使KL散度最小。KL散度等于交叉熵减去熵。对于一个已知的训练集，它的熵是确定的。所以优化KL散度等价于优化交叉熵。而且交叉熵的计算更加简单。

逻辑回归使用交叉熵作为损失函数而不用平方损失，一是因为使用交叉熵可以保证目标函数是凸函数，使用平方损失无法保证；二是使用平方损失的话会出现当输出值接近1或者0的时候，梯度非常小，不容易学习。

15.XGboost 的节点分裂时候，依靠什么？数学形式？XGboost 比GBDT好在哪？

节点的分类是依靠增益来决定的（也就loss founction的降低量），如果增益的下降大于阈值就会继续分裂。
$\frac{1}{2}(\frac{G_L^2}{H_L+\lambda} + \frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})- \gamma$
XGBoost相对于GBDT的优点
- XGBoost的基分类器不仅可以是CART回归树还可以是线性分类器
- XGBoost在目标函数中引入了正则项
- 可以实现并行。但是XGBoost的并行不是在树的粒度上，而是在特征选择的粒度上。树的的生成最耗费时间的内容师选择最优特征，在XGBoost中对特征先进行排序并存储为一个block，在后面的迭代过程重复使用这个block，大大减少了计算量。在进行节点的分裂时，要计算每个特征的增益，最后选择大的增益去做分类，那么这里就可以开多线程来进行特征的增益计算。
- XGBoost还借鉴了随机森林的特征选择，支持列抽样。这可以有效的降低过拟合的风险还可以降低计算量
- XGBoost采用了二阶泰勒近似，同时使用一阶二阶两个信息（二阶信息本身就能让梯度收敛更快更准确）。

17.除了梯度下降，还有啥优化方法？为啥不用牛顿法呢？

18.skip gram和CBOW训练过程中有啥区别？谁更好？

CBOW是利用上下文预测当前中心词。使用GradientDesent方法，不断的去调整周围词的向量。当训练完成之后，每个词都会作为中心词，把周围词的词向量进行了调整，这样也就获得了整个文本里面所有词的词向量。它更适合小的语料库
skip gram是利用当前token预测他的上下文。在skip-gram中，会利用周围的词的预测结果情况，使用GradientDecent来不断的调整中心词的词向量，最终所有的文本遍历完毕之后，也就得到了文本所有词的词向量。它更适合大的语料库。

可以看出，skip-gram进行预测的次数是要多于cbow的：因为每个词在作为中心词时，都要使用周围词进行预测一次。这样相当于比cbow的方法多进行了K次（假设K为窗口大小），因此时间的复杂度为O(KV)，训练时间要比cbow要长。

但是在skip-gram当中，每个词都要收到周围的词的影响，每个词在作为中心词的时候，都要进行K次的预测、调整。因此，当数据量较少，或者词为生僻词出现次数较少时，这种多次的调整会使得词向量相对的更加准确。因为尽管cbow从另外一个角度来说，某个词也是会受到多次周围词的影响（多次将其包含在内的窗口移动），进行词向量的跳帧，但是他的调整是跟周围的词一起调整的，grad的值会平均分到该词上，相当于该生僻词没有收到专门的训练，它只是沾了周围词的光而已。

21.SVM都能用核函数，逻辑回归咋不用呢？

核方法用于分类的时候用的是hinge loss，可以方便的转化为对偶形式求解，也就是SVM。
逻辑回归中交叉熵这个损失函数，对kernel methods来说可能有点伤…转化易求解的形式比较难，而且损失是不是凹函数都不一定。

24.常见的采样方法？

25.如何解决样本不均衡问题？

1.如何解决样本不均衡的问题

上采样（过采样）

上采样方法通过增加分类中少数类样本的数量来实现样本均衡，最直接的方法是简单复制少数类样本形成多条记录，这种方法的缺点是如果样本特征少而可能导致过拟合的问题；经过改进的过抽样方法通过在少数类中加入随机噪声、干扰数据或通过一定规则产生新的合成样本
下采样（欠采样）

下采样方法通过减少分类中多数类样本的样本数量来实现样本均衡，最直接的方法是随机地去掉一些多数类样本来减小多数类的规模，缺点是会丢失多数类样本中的一些重要信息。
通过正负样本的惩罚权重解决样本不均衡

对于分类中不同样本数量的类别分别赋予不同的权重（一般思路分类中的小样本量类别权重高，大样本量类别权重低），然后进行计算和建模。
组合/集成方法

例如，在数据集中的正、负例的样本分别为100和10000条，比例为1:100。此时可以将负例样本（类别中的大量样本集）随机分为100份（当然也可以分更多），每份100条数据；然后每次形成训练集时使用所有的正样本（100条）和随机抽取的负样本（100条）形成新的数据集。如此反复可以得到100个训练集和对应的训练模型。
通过特征选择解决样本不均衡

一般情况下，样本不均衡也会导致特征分布不均衡，但如果小类别样本量具有一定的规模，那么意味着其特征值的分布较为均匀，可通过选择具有显著型的特征配合参与解决样本不均衡问题，也能在一定程度上提高模型效果。

26.高维稀疏特征为啥不适合神经网络训练？

九、面试撕代码

1.最大子序列之和

// 利用动态规划来做
#include
using namespace std;

// 做法一
class Solution{
public:
    int getMaxSumOfSubSeq(vector &nums){
        int len=nums.size();
        vector dp(len+1, 0);
        dp[0] = nums[0];
        int sum=nums[0];
        for(int i=1; i=0) 
                sum+=nums[i];
            else 
                sum=nums[i];
            dp[i] = max(sum, dp[i-1]);
        }
        return dp[len];
    } 
};

// 做法二
class Solution{
public:
    int maxSubArray(vector &nums){
        int pre=0;
        int maxAns=nums[0];
        for(int i=0; i

 
  2.判断一个树是否为二叉搜索树 
  // 递归或中序遍历后看是否为递增序列
#include
using namespace std;

void inOrder(BinaryTree* root, vector &res){
    BinaryTree * pNode = root;
    if(root==nullptr){
        return res;
    }
    
    if(pNode->pLeft != nullptr){
        inOrder(pNode->pLeft, res);
    }
    
    res.push(pNode->valus);
    
    if(pNode->pRight != nullptr){
        inOrder(pNode->pRight, res);
    }
}

int main(){
    vector res;
    inorder(root, res);
    for(int i=1; i
 
  3.找到一个循环链表的循环进口 
  // 剑指offer上的一个题
// 利用快慢指针来做
#include
using namespace std;

// 先找到相遇的结点
ListNode* Meeting(ListNode* pHead){
    if(pHead==nullptr) return nullptr;
    ListNode* pSlow = pHead;
    ListNode* pFast = pHead->next;
    while(pFast != nullptr && pSlow != nullptr){
        if(pFast == pSlow) return pFast;
        pSlow = pSlow->next;
        pFast = pFast->next;
        if(pFast->next != nullptr){
            pFast = pFast->next;
        }
    }
    return nullptr;
}

// 先统计环中的结点个数，再利用快慢指针寻找入口点
ListNode* EntryNodeOfLoop(ListNode* pHead){
    ListNode* meetingNode = Meeting(pHead);
    if(meetingNode == nullptr) return nullptr;
    ListNode* pNode = meetingNode;
    int countor = 1;
    pNode = pNode->next;
    while(pNode != meetingNode){
        countor++;
        pNode = pNode->next;
    }
    
    ListNode* pFast = pHead;
    ListNode* pSlow = pHead;
    for(int i=0; inext;
    }
    
    while(pFast != pSlow){
        pFast = pFast->next;
        pSlow = pSlow->next;
    }
    return pFast;
}

int main(){
    
}
 
  4.两个有序数组，随意挑选两个值求其和求第k大的组合 
  // 可以使用一个map记录所有可能的数的组合
#include
using namespace std;

int getSumTopK(vector &arr1, vector &arr2, int k){
    map hash;
    for(int i=0; i::iterator iter = hash.begin(); // map的遍历
    // auto iter = hash.begin(); // 这也可以作为map的遍历
    int res = 0;
    while(k>=0 && iter!=hash.end()){
        if(k<=iter->second){
            return iter->first;
        }
        k-=iter->second;
        iter++;
    }
    return 0;
}

int main(){
    vector arr1={1,2,3};
    vector arr2={2,3,5};
    int res = getSumTopK(arr1, arr2, 8);
    cout << res << endl;
    return 0;
}
 
  5.层序遍历二叉树 
  // 利用队列来做并且设定好两个记录变量m和n，只要队列不为空就一直打印
class Solution{
public:
    void PrintFromTopToBottom(BinaryTreeNode* pTreeRoot){
        if(!pTreeRoot) return;
        deque dequeTreeNode;
        dequeTreeNode.push_back(pTreeRoot);

        while(dequeTreeNode.size()){
            BinaryTreeNode *pNode = dequeTreeNode.front();
            dequeTreeNode.pop_front();
            cout << pNode->m_nValue << endl;
            if(pNode->m_pLeft != nullptr){
                dequeTreeNode.push_back(pNode->m_pLeft);
            }

            if(pNode->m_pRight != nullptr){
                dequeTreeNode.push_back(pNode->m_pRight);
            }
        }
    }
};

 
  6.一个排序数组能够构成多少个二叉搜索树 
  // 如果不是排序数组就先排一下序
// 每一个数都有可能是一个根节点
class Solution {
public:
    int numTrees(vector &nums) {
        int n=nums.size();
        vector dp(n + 1, 0); // dp[i]代表i个数字有多少个排列方式
        dp[0] = dp[1] = 1;
        for(int i = 2; i <= n; ++i)
        {
            for(int j = 1; j <= i; ++j)
            {
                //G(i) += G(j - 1) * G(n - j)
                dp[i] += dp[j - 1] * dp[i - j]; // 为什么j从1开始遍历，因为要拿出来一个数字作为根节点
            }
        }
        return dp[n];
    }
};
 
  7.中序遍历 非递归 
  // 递归版本的遍历
class Solution{
public:
    void Inorder(BinaryTree* root){
        if(root == NULL) return NULL;
        Inorder(root->left);
        cout << root->val << endl;
        Inorder(root->right);
    }
};

// 非递归版本
void InOrderWithoutRecursion1(BTNode* root)
{
	//空树
	if (root == NULL)
		return;
	//树非空
	BTNode* p = root;
	stack s;
	while (!s.empty() || p)
	{
		//一直遍历到左子树最下边，边遍历边保存根节点到栈中
		while (p)
		{
			s.push(p);
			p = p->lchild;
		}
		//当p为空时，说明已经到达左子树最下边，这时需要出栈了
		if (!s.empty())
		{
			p = s.top();
			s.pop();
			cout << setw(4) << p->data;
			//进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)
			p = p->rchild;
		}
	}
}
 
  8.给一个前序遍历和中序遍历写出来后序遍历 
  // 首先重构二叉树，然后递归得到后序遍历
class Solution {
public:
    TreeNode* buildTree(vector& preorder, vector& inorder) {
        int pres=0,ins=0;
        int pree=int(preorder.size()-1),ine=int(inorder.size()-1);
        return myBT(inorder,preorder,pres,pree,ins,ine);
    }

    TreeNode* myBT(vector& inorder, vector& preorder,int pres, int pree, int ins, int ine){
        TreeNode* root;int mid;
        if(pres > pree || ins > ine )
            return NULL;
        root = new TreeNode(preorder[pres]);
        for(int i=0;ileft = myBT(inorder,preorder,pres+1,pres+mid-ins,ins,mid-1);
        root->right = myBT(inorder,preorder,pree-(ine-mid)+1,pree,mid+1,ine);
        return root;
    }
};

// 后序遍历，递归版本
void laterOrder(TreeNode* root){
    if(root ==NULL) return;
    laterOrder(root->left);
    laterOrder(root->right);
    cout << root->val << endl;
}
 
  9. 无序数组，整数，最长上升子序列的长度 
  // DP来做（也可以使用暴力解来做）
class Solution {
public:
    int lengthOfLIS(vector& nums) {
        int n=(int)nums.size();
        if (n == 0) return 0;
        vector dp(n, 0);
        for (int i = 0; i < n; ++i) {
            dp[i] = 1;
            for (int j = 0; j < i; ++j) {
                if (nums[j] < nums[i]) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};
 
  10.累加数 Leetcode 306 
  11.二叉树任两节点的最近公共祖先 
  // 如果是二叉搜索树
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if (root == NULL) return root;
        while(root!=NULL){
            if(root->val > p->val && root->val > q->val){
                root = root->left;
            }
            
            else if(root->val < p->val && root->val < q->val){
                root = root->right;
            }
            
            else{
                break;
            }
        }
        return root; 
    }
};
 
  // 如果是普通二叉树。我们需要知道两个结点所在的路径，然后去搜索公共结点
class Solution{
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if (root == nullptr){
            return nullptr;
        }

        vector v1; // 保存p的路径
        vector v2; // 保存q的路径
        TreeNode* res = nullptr;

        bool flag1 = findPath(root, p, v1);
        bool flag2 = findPath(root, q, v2);

        if(flag1 == true && flag2 == true){
            int i=0, j=0;
            while(i &path){
        bool flag = false;
        path.push_back(root);
        cout << "push_back: " << root->val << endl;
        if(root == target){
            cout << "have found" << endl;
            return true;
        }

        if(root->left != nullptr && flag == false){
            flag = findPath(root->left, target, path);
        }

        if(root->right != nullptr && flag == false){
            flag = findPath(root->right, target, path);
        }
        
        // 什么时候弹出去
        if(flag == false){
            cout << "have poped: " << root->val << endl;
            path.pop_back();
        }
        return flag;
    }
};
 
  12. topk-找第k大的数 
  // 这个题可以使用快排的思想来做
class Solution {
public:
    int findKthLargest(vector& nums, int k) {
        sort(nums.begin(), nums.end());
        int current = nums[0];
        for(int i=nums.size()-1; i>=0 && k>0;i--){
            current = nums[i];
            k--;
        }
        return current;
    }
};

// 利用堆来实现
class Solution2{
public:
    int findKthLargest(vector& nums, int k) {
        priority_queue, greater> pq; // 升序
        // priority_queue ,less >q; // 降序   
        for (auto n : nums) {
            if (pq.size() == k && pq.top() >= n) {
                cout << "pq.top()" << pq.top() << endl;
                continue;
            }
            if (pq.size() == k) {
                cout << "pq.pop()elements: " << pq.top() << endl;
                pq.pop();
            }
            
            pq.push(n);
        }
        return pq.top();
    }
};

 
  13.a的n次方 
  // 利用递归+快速幂来做
class Solution{
public:
    double myPow(double x, int n) {
        double res = 1;
        if(n==0) return 1;
        if(n==1) return x;
        if(n==-1) return 1.0/x;

        long num = n;
        if(n<0) num=-num;
        res = myPow(x*x, num/2);
        if(num%2==1){
            res*=x;
        }
        return n>0?res:(1.0/res);
    }
};
 
  14.最长不重复子串 
  // 利用map来做
#include
using namespace std;

class Solution{
public:
    int lengthOfLongestSubstring(string s){
        map hash;
        int start=0;
        int end=0;
        int res=0;
        int len = s.size();
        while(start
 
  15.B树是否为A树的子树 
  // 利用递归的思想来做
class Solution {
public:
    bool helper(TreeNode* A, TreeNode* B) { // 判断两个树是否完全一样
        if (A == NULL || B == NULL) {
            return B == NULL ? true : false;
        }
        if (A->val != B->val) {
            return false;
        }
        return helper(A->left, B->left) && helper(A->right, B->right);
    }
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if (A == NULL || B == NULL) {
            return false;
        }
        return helper(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
    }
};
 
  16. 二叉树的之字形遍历 
  // 利用栈和队列来做
// 利用队列和栈来实现
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> res;
        if(root==NULL) return res;
        
        int m=1, n=0,flag=0;
        TreeNode* pNode=NULL;
        queue treeQueue;
        stack treeStack;

        treeQueue.push(root);
        while (!treeQueue.empty())
        {
            n=m;
            m=0;
            vector mid;
            if(flag==0){
                for(int i=0; ival);
                    if(pNode->left!=NULL){
                        treeQueue.push(pNode->left);
                        m++;
                    }

                    if(pNode->right != NULL){
                        treeQueue.push(pNode->right);
                        m++;
                    }
                    treeQueue.pop();
                }
                res.push_back(mid);
                flag=1;
            }

            else{
                for(int i=0; ileft!=NULL){
                        treeQueue.push(pNode->left);
                        m++;
                    }

                    if(pNode->right!=NULL){
                        treeQueue.push(pNode->right);
                        m++;
                    }
                    treeQueue.pop();
                }

                while (!treeStack.empty()) // 打印栈内的数值
                {
                    pNode=treeStack.top();
                    mid.push_back(pNode->val);
                    treeStack.pop();
                }
                res.push_back(mid);
                flag=0; 
            }
        }
        return res;
    }
};
 
  17.找出正整数数组中和为S的连续子数组数量 
  class Solution {
public:
    vector> findContinuousSequence(vector &nums, int target) {
        vector> res;
        vector mid;
        int len=nums.size();
        if(len==0) return res;
        findCore(nums, target, res, mid, 0, 0);
        return res;
    }

    void findCore(vector &nums, int target, vector> &res, vector &mid, int curSum, int i){
        if(curSum==target){
            res.push_back(mid);
        }

        if(i==nums.size()) return;
        for(int j=i; j
 
  18.小偷隔一家偷东西(类似于小Q爬塔的问题) 
  #include
using namespace std;

class Solution {
public:
    int rob(vector& nums) {
        int len = nums.size();
        if(len==0){return 0;}
        vector maxprofit(len+1, 0);
        maxprofit[0] = 0;
        maxprofit[1] = nums[0];
        for(int i=2; i<=len; i++){
            maxprofit[i] = max(maxprofit[i-1], maxprofit[i-2]+nums[i-1]);
        }
        return maxprofit[len];
    }
};
 
  19.手写冒泡排序 
  #include
using namespace std;

vector bubbleSort(vector &datas){
    int len = datas.size();
    for(int i=0; i datas[j+1]){
                int temp = datas[j];
                datas[j] = datas[j+1];
                datas[j+1] = temp;
            }
        }
    }
    return datas;
}
 
  20.输入N个点坐标，寻找面积最大的矩形 
  21. 二叉树的后续遍历（非递归） 
  // 递归版本
void postOrder1(BinTree *root) {
    if(root == NULL) return;
    else{
        postOrder1(root->left);
        postOrder1(root->right);
        cout << root->val << endl;
    }
}

// 非递归版本
void postOrder2(BinTree *root)    //非递归后序遍历
{
    stack s;
    BinTree *p=root;
    BTNode *temp;
    while(p!=NULL||!s.empty())
    {
        while(p!=NULL)              //沿左子树一直往下搜索，直至出现没有左子树的结点 
        {
            BTNode *btn=(BTNode *)malloc(sizeof(BTNode));
            btn->btnode=p;
            btn->isFirst=true;
            s.push(btn);
            p=p->lchild;
        }
        if(!s.empty())
        {
            temp=s.top();
            s.pop();
            if(temp->isFirst==true)     //表示是第一次出现在栈顶 
             {
                temp->isFirst=false;
                s.push(temp);
                p=temp->btnode->rchild;    
            }
            else//第二次出现在栈顶 
             {
                cout<btnode->data<<"";
                p=NULL;
            }
        }
    }    
} 
 
  22. 最长公共子序列 
  // 采用动态规划来做
// 最长公共子序列
#include
using namespace std;

class SolutionMaxSubSequence{
public:
    // 递归
    int dp(string str1, string str2, int i, int j){
        if(i==-1 || j==-1){
            return 0;
        }
        else if(str1[i] == str2[j]){
            return dp(str1, str2, i-1, j-1)+1;
        }

        else
        {
            return max(dp(str1, str2, i-1, j), dp(str1, str2, i, j-1));
        }
    }

    int mian_(string s1, string s2){
        if(s1==s2) return s1.size();
        int len1 = s1.size();
        int len2 = s2.size();
        if(len1==0 || len2==0){
            return 0;
        }
        return dp(s1, s2, len1-1, len2-2);
    }

    // 转化为动态规划问题
    int mainDP(string s1, string s2){
        if(s1==s2) return s1.size();
        int len1 = s1.size();
        int len2 = s2.size();
        vector > dp(len1+1, vector(len2+1, 0));
        for(int i=1; i<=len1; i++){
            for(int j=1; j<=len2; j++){
                if(s1[i-1] == s2[j-1]){
                    dp[i][j] = 1+dp[i-1][j-1];
                }

                else{
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
        return dp[len1][len2];
    }
};

 
  23. 二叉树最长路径长度 
  // 基于递归的方法
class BinaryTreeMaxPath{
public:
    int getRes(TreeNode* root){
        if(root==NULL) return 0;
        int l = getRes(root->left)+1;
        int r = getRes(root->right)+1;
        int maxDepth = l>r?l:r;
        return maxDepth;
    }
};

// 求最长路径长度也可以基于层序遍历来求最大深度
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==NULL) return 0;
        queue q;
        q.push(root);
        int depth = 1;
        while (!q.empty()) // 当我们的队列不为空的时候
        {
            int qsize = q.size();
            for(int i=0; ileft != NULL){ // 把pNode的相邻结点全部加入到队列
                    q.push(pNode->left);
                }

                if(pNode->right != NULL){
                    q.push(pNode->right);
                }
                q.pop();
            }

            depth++; // 增加步数
        }
       return depth;    
    }
};

// 拓展题目，求最大路径和
class Solution {
public:
    int res=INT_MIN; // 全局变量
    int maxPathSum(TreeNode* root) {
        getmax(root);
        return res;
    }
    
    int getmax(TreeNode* root){
        if(!root) 
            return 0;
        // 计算左边分支最大值，左边分支如果为负数还不如不选择
        int left=max(getmax(root->left),0);
        // 计算右边分支最大值，右边分支如果为负数还不如不选择
        int right=max(getmax(root->right),0);
        // left->root->right 作为路径与历史最大值做比较
        res=max(res,root->val+left+right);
        // 返回经过root的单边最大分支给上游
        return max(left,right)+root->val;
    }
};
 
  24. 反转字符串 
  //直接reverse就可以反转字符串
#include
using namespace std;

class ReverseString{
public:
    string reverseString(string s){
        int len = s.size();
        if(len==1) return s;
        string res = "", temp="";
        for(int i=0; i
 
  25. 全排列问题 
  class Solution{
public:
	void swap(vector &a, int i, int j){
        int temp = 0;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp
    }
    
    void save(vector &a, int q){
        for(int i=0; i&a, int p, int q){
        if(p==q){
            save(a, q+1);
        }
        
        else{
            for(int i=p; i<=q; i++){
                swap(a, i, p);
                main_(a, p+1, q);
                swap(a, i, p);
            }
        }   
    }
};
 
  26. 未出现的最小整数 
  27. 之字型打印二叉树 
  // 利用队列和栈来实现
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> res;
        if(root==NULL) return res;
        
        int m=1, n=0,flag=0; // flag是正反序打印的标志位
        TreeNode* pNode=NULL;
        queue treeQueue;
        stack treeStack;

        treeQueue.push(root);
        while (!treeQueue.empty())
        {
            n=m;
            m=0;
            vector mid;
            if(flag==0){
                for(int i=0; ival);
                    if(pNode->left!=NULL){
                        treeQueue.push(pNode->left);
                        m++;
                    }

                    if(pNode->right != NULL){
                        treeQueue.push(pNode->right);
                        m++;
                    }
                    treeQueue.pop();
                }
                res.push_back(mid);
                flag=1;
            }

            else{
                for(int i=0; ileft!=NULL){
                        treeQueue.push(pNode->left);
                        m++;
                    }

                    if(pNode->right!=NULL){
                        treeQueue.push(pNode->right);
                        m++;
                    }
                    treeQueue.pop();
                }

                while (!treeStack.empty())
                {
                    pNode=treeStack.top();
                    mid.push_back(pNode->val);
                    treeStack.pop();
                }
                res.push_back(mid);
                flag=0;
                
            }
        }
        return res;
    }
};
 
  28. 顺时针打印数组 
  class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        vector ans;
        int R,C;
        if(!(R=matrix.size()) || !(C=matrix[0].size())){
            return ans;
        }

        int top=0,left=0,right=C-1,bottom=R-1;
        while(ans.size() < R*C){
            //遍历上边
            for(int i=left;i<=right;++i) ans.push_back(matrix[top][i]);
            //遍历右边
            for(int i=top+1;i=left && bottom > top;--i) ans.push_back(matrix[bottom][i]);
            //遍历左边
            for(int i=bottom-1;i>top && left < right;--i) ans.push_back(matrix[i][left]);
            top++;bottom--;
            left++;right--;
        }
        return ans;
    }
};
 
  29. 实现带精度的sqrt 
  // 按照数学推导直接计算
class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = exp(0.5 * log(x)); // x=e^{1/2 * log(x)}
        return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans); // 取整
    }
};

// 二分查找
double getSqrt(int x,double precision) {
	 double left = 0, right = x;
	 while (1) {
		 double mid = left + (right - left) / 2;
		 if (abs(x /mid - mid) < precision)	
             return mid;
		 else if (x / mid > mid)	
             left = mid + 1;
		 else 
             right = mid - 1;
	 }
}
 
  30. 实现pow 
  class Solution { // 快速幂
public:
    double myPow(double x, int n) {
        if(x == 1 || n == 0) return 1;
        double ans = 1;
        long num = n;
        if(n < 0){
            num = -num;
            x = 1/x;
        }
        
        while(num){
            if(num & 1) ans *= x; 
            x *= x;
            num >>= 1;
        }
        return ans;
    }
};
 
  字符串分割，多个分隔符(前缀树) 
  字符串匹配问题 
  有足够多的数据（内存无法一次性装下），如何获得最大的k个数 
  给一个无序数组，输出最小的不在数组中的正数 
  数组分为两部分，使得他们和的差值最小 
  两颗二叉树合并 
  多个字符串，给定前缀和长度比例阈值，返回符合条件的字符串个数 
  给定字符矩阵，单词，判断矩阵里有没有该一条路径组成该单词 
  31. 优先队列的实现 
  template 
class priqueue{
public:
	priqueue(int m){//构造函数传入队列的总长度
		maxsize=m;
		x=new T[maxsize+1];//这里为了计数方便，让下标从1开始
						   //此时，如果一个元素下标为i，则它的
		                                   //左子节点在数组中的下标就是2i
		                                   //右子节点在数组中的下标是2i+1
		n=0;
	}
	void Add(T t){//这里构建一个小顶堆
		x[++n]=t;
		int p;
		for(int i=n;i>1 && x[p=i/2]>x[i];i=p){
			swap(p,i);
		}
	}
    
	T extractMin(){
		T temp=x[1];//取出堆顶权值最大的那个元素
		x[1]=x[n--];//序列长度减1，并将最后一个元素放在堆顶
		int p;
		for(int i=1;(p=2i)x[p+1])
				p++;
			if(x[p]>=x[i])//移动到位
				break;
			swap(p,i);
		}
		return temp;
	}
    
private:
	int n;//队列中元素个数
	int maxsize;//整个队列的总长度
	T *x;//队列指针
	void swap(int i,int j){
		T temp=x[i];
		x[i]=x[j];
		x[j]=temp;
	}
}
 
  32. LRU缓存的实现 
  // C++版本实现
class LRUCache {
    list> l;
    unordered_map>::iterator> mp;
    int cap;
public:
    LRUCache(int capacity) {
        cap = capacity;
    }
    
    int get(int key) {
        if(mp.find(key) != mp.end())
        {
            int res = (*mp[key]).second;
            l.erase(mp[key]);
            l.push_front(make_pair(key, res));
            mp[key] = l.begin();
            return res;
        }
        return -1;
    }
    
    void put(int key, int value) {
        if(mp.find(key) != mp.end())
        {
            l.erase(mp[key]);
            l.push_front(make_pair(key, value));
            mp[key] = l.begin();
        }
        else
        {
            if(l.size() == cap)
            {
                mp.erase(l.back().first);
                l.pop_back();
            }
            l.push_front(make_pair(key, value));
            mp[key] = l.begin();
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */
 
  33. 单链表的升序排列 
  // 这也是逐个遍历交换节点的val，但是不涉及指针的改变
list_node * selection_sort(list_node * head,int n){
    //在下面完成代码
    list_node* cur = head;
    list_node* ans = cur;
    while(cur != nullptr){
        int Min = cur->val; // 假设当前值是最小值
        list_node* m = cur;
        head = cur->next;
        while(head != nullptr){
            if(head->val < Min){ // 如果是降序排列就直接把这里的<改成>
                m = head; 
                Min = head->val;
            }
            head = head->next;
        }
        swap(cur->val,m->val);
        cur = cur->next;
    }
    return ans;
}
 
  针对快手的面试题目 
  1. 链表反转 
  #include
using namespace std;

struct ListNode{
    int       m_nKey;
    ListNode* m_pNext;
};

ListNode* ReverseList(ListNode *pHead){
    if(pHead==nullptr){
        return nullptr;
    }

    ListNode* pReversedHead = nullptr;
    ListNode* pNode = pHead;
    ListNode* pPrev = nullptr;
    while(pNode != nullptr){
        ListNode* pNext = pNode->m_pNext;
        if(pNext==nullptr){
            pReversedHead = pNode;
        }
        pNode->m_pNext = pPrev;
        pPrev = pNode;
        pNode = pNext;
    }
    return pReversedHead;
}
 
  2. 整数反转 
  class Solution {
public:
    int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            int pop = x % 10;
            x /= 10;
            if (rev > INT_MAX/10 || (rev == INT_MAX / 10 && pop > 7)) 
                return 0;
            if (rev < INT_MIN/10 || (rev == INT_MIN / 10 && pop < -8)) 
                return 0;
            rev = rev * 10 + pop;
        }
        return rev;
    } 
};
 
  3. 排序链表的合并 
  ListNode* MergeRepeat(ListNode* pHead1, ListNode* pHead2){
    if(l1==NULL) return l2;
    if(l2==NULL) return l1;
    if(l1->val <= l2->val){
        l1->next = MergeRepeat(l1->next, l2);
        return l1;
    }
    else{
        l2->next = MergeRepeat(l1, l2->next);
        return l2
    }
}
 
  4. K个排序链表的合并 
  // 方法一
class Solution{
public:
    // 递归合并两个有序链表
    ListNode* merge(ListNode* p1, ListNode* p2){
        if(!p1) return p2; // 递归终止条件
        if(!p2) return p1;
        if(p1->val <= p2->val){
            p1->next = merge(p1->next, p2);
            return p1; // 最后的返回值
        }else{
            p2->next = merge(p1, p2->next);
            return p2;
        }
    }

     ListNode* mergeKLists(vector& lists) {
        if(lists.size() == 0) return nullptr;
        ListNode* head = lists[0];
        for(int i = 1; i& lists) {
        ListNode* pNode = nullptr;
        vector elements;
        for(int i=0; ival);
                pNode = pNode->next;
            }
        }
        sort(elements.begin(), elements.end());
        ListNode* res = new ListNode(-1);
        ListNode* ptr;
        ptr = res;
        for(int j=0; jnext = new ListNode(elements[j]);
            ptr = ptr->next;
        }
        return res->next; 
    }
};
 
  5. 最大子序列和 
  // 利用动态规划来做
#include
using namespace std;

// 做法一
class Solution{
public:
    int getMaxSumOfSubSeq(vector &nums){
        int len=nums.size();
        vector dp(len+1, 0);
        dp[0] = nums[0];
        int sum=nums[0];
        for(int i=1; i=0) sum+=nums[i];
            else sum=nums[i];
            dp[i] = max(sum, dp[i-1]);
        }
        return dp[i];
    } 
};

// 做法二
class Solution{
public:
    int maxSubArray(vector &nums){
        int pre=0;
        int maxAns=nums[0];
        for(int i=0; i
 
  6. 给定三个点和一个目标点，判断点在不在三角形之内 
  7. 数组重排列，奇数放在左边，偶数放在右边 
  // 方法一: 暴力解。可以保证排后数据的相对位置不改变
// 方法二: 设置两个指针，遇到一个奇数和偶数时进行交换，但是这个不能保证数据的相对顺序固定不变。
 
  9. 二维矩阵从左上角到右下角的路径数量 
  // 题目就是不同路径的问题
// 利用动态规划，可以是一维的数组，也可以是一个二维矩阵
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector> dp(m, vector(n, 0));
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                dp[i][j] = (i > 0 && j >0 ) ? dp[i][j] = dp[i][j-1] + dp[i-1][j] : 1;
            }
        }
        return dp[m-1][n-1];
    }
};

// 拓展到存在障碍的路径问题
class Solution {
public:
    int uniquePathsWithObstacles(vector>& obstacleGrid) {
        int m = obstacleGrid.size();
        if (m < 1) return 0;
        int n = obstacleGrid[0].size();
        if (n < 1) return 0;
        long dp[m][n];  //　使用int提交出现溢出错误，就改为long
        if (1 == obstacleGrid[0][0]) return 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (0 == i && 0 == j) {     //上面判断过(０,０)为１的情况了，这里必定是没有障碍物，因此路径为１
                    dp[i][j] = 1;
                } else if (0 == i && j != 0) {  //　最上面一行网格，如果该点是障碍物，则这一点必定不可达，否则路径和达到其左侧的路径一样
                    dp[i][j] = (1 == obstacleGrid[i][j] ? 0 : dp[i][j - 1]);
                } else if (0 != i && j == 0) { //　最左侧一列网格，如果该点是障碍物，则这一点必定不可达，否则路径和达到其上侧的路径一样
                    dp[i][j] = (1 == obstacleGrid[i][j] ? 0 : dp[i - 1][j]);
                } else {    //　对于坐标均不为０的点，仅在该点为障碍物的时候不可达
                    dp[i][j] = (1 == obstacleGrid[i][j] ? 0 : dp[i][j - 1] + dp[i - 1][j]);
                }
            }
        }
        return static_cast(dp[m - 1][n - 1]);
    }
};
 
  针对猿辅导的题目 
  1. leetcode1419青蛙叫 
  class Solution {
public:
    int minNumberOfFrogs(string croakOfFrogs) {
        int c=0;
        int r=0;
        int o=0;
        int a=0;
        int k=0;
        int re=0;
        bool flag=true;
        for(int i=0; i=r && r>=o && o>=a && a>=k){
                c--;
                r--;
                o--;
                a--;
                k--;
                }  
            }
            if(!(c>=r && r>=o && o>=a && a>=k)){//必须保持任意时刻（c>=r>=o>=a>=k）,才是正确的；否则就是错误的，
                flag=false;
                break;
            }       
        }
        if (c!=0 || r!=0 || o!=0 || a!=0 ||k!=0) flag=false;//如果最后有剩的字母，也是错误的
        if (flag==true) return re;
        else return -1;
    }
};
 
  2. 判断一个二叉树是否对称 
  //直接输入两颗树判断左右子树是否相等
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return isSymmetric(root, root);
    }

    bool isSymmetric(TreeNode* root1, TreeNode* root2){
        if(root1==NULL && root2==NULL){
            return true;
        }

        else if(root1==NULL || root2==NULL){
            return false;
        }

        else if(root1->val != root2->val){
            return false;
        }
        return isSymmetric(root1->left, root2->right) && isSymmetric(root1->right, root2->left);
    }
};
 
  3. 最长合法的括号匹配 
  int longestValidParentheses(string s) {
        stack left;//position of '('
        for(int ii = 0; ii < s.size(); ++ii){
            if (s[ii] == '(') left.push(ii);
            else if (!left.empty()){ //')'
                s[ii] = 'k';
                s[left.top()] = 'k';
                left.pop();
            }
        }
        int maxLength = 0;
        int length = 0;
        for(int ii = 0; ii < s.size(); ++ii){
            if (s[ii]=='k'){
                ++length;                
                if (maxLength < length) maxLength = length;
            }
            else length = 0;
 
        }
        return maxLength;
    }
};
 
  5. 删除单链表中的重复结点 
  // 1->1->1->2->3  输出：2->3

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) : val(x), next(NULL) { }
};
*/

class Solution {
public:
    ListNode* deleteDuplication(ListNode* pHead)
    {
          // 链表有0个/1个节点，返回第一个节点
          if(pHead==NULL || pHead->next==NULL)
              return pHead;
          else
          {
              // 新建一个头节点，防止第一个结点被删除
              ListNode* newHead=new ListNode(-1);
              newHead->next=pHead;

              // 建立索引指针
              ListNode* p=pHead;      // 当前节点
              ListNode* pre=newHead;  // 当前节点的前序节点
              ListNode* next=p->next;    // 当前节点的后序节点

              // 从头到尾遍历编标
              while(p!=NULL && p->next!=NULL)
              {
                  if(p->val==next->val)//如果当前节点的值和下一个节点的值相等
                  {
                      // 循环查找，找到与当前节点不同的节点
                      while(next!=NULL && next->val==p->val)
                      {
                          ListNode* temp=next;
                          next=next->next;

                          // 删除内存中的重复节点
                          delete temp;
                          temp = nullptr;

                      }

                    pre->next=next;
                    p=next;
                  }
                  else//如果当前节点和下一个节点值不等，则向后移动一位
                  {
                      pre=p;
                      p=p->next;
                  }
                  next=p->next;
              }
           return newHead->next;//返回头结点的下一个节点
          }
    }
};
 
  6. 矩阵中的最长递增路径 
  class Solution{
public:
    static constexpr int dirs[4][2] = {
    {1,0}, {-1, 0}, {0, 1}, {0, -1}};
    int longestIncreasingPath(vector< vector > &matrix){
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return 0;
        }
        int m=matrix.size();
        int n=matrix[0].size();
        auto mem = vector> (m, vector(n,0));
        int res=0;
        
        for(int i=0; i > &matrix, vector> &mem){
        if(mem[i][j] != 0){
            return mem[i][j];
        }

        ++mem[i][j];
        for(int dir=0; dir<4; dir++){
            int newi= i+dirs[dir][0];
            int newj= j+dirs[dir][1];
            if(newi>=0 && newi=0 && newj matrix[i][j]){
                mem[i][j]=max(mem[i][j], dfs(newi, newj, m, n, matrix, mem)+1);
            }
        }
        return mem[i][j];
    }
};
 
  7. 最长回文子串（leetcode 516） 
  int longestPalindromeSubseq(string s) {
    int n = s.size();
    // dp 数组全部初始化为 0
    vector> dp(n, vector(n, 0));
    // base case
    for (int i = 0; i < n; i++)
        dp[i][i] = 1;
        
    // 反着遍历保证正确的状态转移
    for (int i = n - 1; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            // 状态转移方程
            if (s[i] == s[j])
                dp[i][j] = dp[i + 1][j - 1] + 2;
            else
                dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
    // 整个 s 的最长回文子串长度
    return dp[0][n - 1];
}

 
  剑指offer题目 
  1. 矩阵中的路径 
  /*
题目描述：给定一个字符矩阵，判断某个路径是否能组成某个字符串
*/
class Solution{
public:
    static constexpr int dirs[4][2] = {
    {1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    int rows;
    int columns;
    bool exist(vector>& board, string word){
        rows = board.size();
        columns = board[0].size();
        if(rows==1 && columns==1 && word.size()==1 ){
            if(word[0] == board[0][0]){
                return true;
            }
            else{
                return false;
            }
        }

        // 遍历每个起点
        for(int i=0; i>& board, string word, int path, int row, int col){
        if(path == word.size()){
            return true;
        }

        else if(row>=0 && col>=0 && row=0 && newCol>=0 && newRow>& board, string word) {
	bool m=false;
	for(int i=0;i>& board,string&word ,int row,int col,int Pos)
{
	if (row >= board.size() || row < 0 || col >= board[0].size() || col < 0 || board[row][col]!=word[Pos]) return false;
	if (Pos == word.size() - 1) return true;
	char tmp = board[row][col];
	board[row][col] = '#';
	bool m=false;
	m = dfs(board, word, row + 1, col, Pos + 1) || dfs(board, word, row - 1, col, Pos + 1) || dfs(board, word, row, col + 1, Pos + 1)||dfs(board, word, row, col - 1, Pos + 1);
	board[row][col] = tmp;
	return m;
}
 
  2. 机器人的运动范围 
  class Solution {
public:
    int movingCount(int m, int n, int k) {
        if(k == 0) return 1;
        vector > valid(m, vector(n, true)); // 记录该位置是否被访问过
        return dfs(valid, m, n, 0, 0, k);
    }
    int dfs(vector >& valid, int m, int n, int row, int col, int k) // valid的传值一定要用 & ！！！
    {
        int sum = getSum(row) + getSum(col);
        // 如果越界，或者和大于k，或者已被访问过了，返回0
        if(row>=m || col>=n || sum>k || !valid[row][col]) return 0;
        valid[row][col] = false; // 该位置状态变为：已访问过
        return 1 + dfs(valid,m,n,row+1,col,k) + dfs(valid,m,n,row,col+1,k); // 回溯法（递归）
    }
    int getSum(int num)
    {
        // 求某个数字所有位数相加的和
        if(num < 10) return num;
        int sum = 0;
        while(num > 0)
        {
            sum += num % 10;
            num /= 10;
        }
        return sum;
    }
};
 
  3. 正则表达式匹配 
  /*
请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。
*/

bool isMatch(std::string s, std::string p) {
    if (p.empty()) {
        return s.empty();
    }

    // p,s第一个字符是否匹配，相等或为 '.'
    bool first_match = (!s.empty() && (p[0] == s[0] || p[0] == '.'));

    // 从p的第2个字符开始，如果为 '*'
    if (p.size() >= 2 && p[1] == '*') {
        // 考虑 '*' 表示前面字符0次和多次的情况
        // 0次：s回溯与p第3个字符继续下一轮匹配
        // 多次 : 第1个字符匹配，从s第2个字符与p继续下一轮匹配
        return (isMatch(s, p.substr(2)) || (first_match && isMatch(s.substr(1), p)));
    } else {
        //未匹配到 '*'，继续普通匹配
        return first_match && isMatch(s.substr(1), p.substr(1));
    }
}
 
  4. 数组中的逆序对 
  class Solution {
private:
    int cnt=0; // 记录总的逆序对数
public:
    void mergesort(int lo,int hi,vector& nums,vector& tmp){
        if(lo>=hi) return;
        int mid=lo+(hi-lo)/2;
        //cout << "mid: " << mid << endl;
        mergesort(lo,mid,nums,tmp); // 一直二分
        mergesort(mid+1,hi,nums,tmp);

        //cout << "mid1: " << mid << endl;

        int i=lo,j=mid+1;
        //cout << "i: " << i << " " << "j: " << j << endl;
        for(int k=lo;k<=hi;k++){
            if(i>mid) tmp[k]=nums[j++];//nums[i]到nums[mid]已经全部填入tmp
            else if(j>hi) tmp[k]=nums[i++];//nums[mid+1]到nums[j]已经全部填入tmp
            else if(nums[i]>nums[j]) {
                tmp[k]=nums[j++];
                cnt+=mid-i+1;//i肯定小于j，且nums[i]到nums[mid]是升序排序，如果nums[i]>nums[j]，说明从nums[i]到nums[mid]和nums[j]都是逆序对
            }
            else tmp[k]=nums[i++];
        }
        for(int m=lo;m<=hi;m++) nums[m]=tmp[m];//
    }

    int reversePairs(vector& nums) {
        vector tmp(nums.size(),0);//就是用来记录某个递归函数merge后的情况，然后复制更新nums
        mergesort(0,nums.size()-1,nums,tmp);
        return cnt;
    }
};

 
  二叉树的最近公共祖先 
  class Solution{
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        if (root == nullptr){
            return nullptr;
        }

        vector v1; // 保存p的路径
        vector v2; // 保存q的路径
        TreeNode* res = nullptr;

        bool flag1 = findPath(root, p, v1);
        bool flag2 = findPath(root, q, v2);
        cout << flag1 << " " << flag2 << endl;

        if(flag1 == true && flag2 == true){
            int i=0, j=0;
            while(i &path){
        bool flag = false;
        path.push_back(root);
        if(root == target){
            return true;
        }

        if(root->left != nullptr && flag == false){
            flag = findPath(root->left, target, path);
        }

        if(root->right != nullptr && flag == false){
            flag = findPath(root->right, target, path);
        }

        if(flag == false){
            path.pop_back();
        }
        return flag;
    }
};
 
  十、 基础实现题目 
  1. 归并排序 
  void Merge(int arr[],int low,int mid,int high);
void MergeSort (int arr [], int low,int high) {
    if(low>=high) { return; } // 终止递归的条件，子序列长度为1
    int mid =  low + (high - low)/2;  // 取得序列中间的元素
    MergeSort(arr,low,mid);  // 对左半边递归
    MergeSort(arr,mid+1,high);  // 对右半边递归
    Merge(arr,low,mid,high);  // 合并
  }

void Merge(int arr[],int low,int mid,int high){
    //low为第1有序区的第1个元素，i指向第1个元素, mid为第1有序区的最后1个元素
    int i=low,j=mid+1,k=0;  //mid+1为第2有序区第1个元素，j指向第1个元素
    int *temp=new int[high-low+1]; //temp数组暂存合并的有序序列
    while(i<=mid&&j<=high){
        if(arr[i]<=arr[j]) //较小的先存入temp中
            temp[k++]=arr[i++];
        else
            temp[k++]=arr[j++];
    }
    while(i<=mid)//若比较完之后，第一个有序区仍有剩余，则直接复制到t数组中
        temp[k++]=arr[i++];
    while(j<=high)//同上
        temp[k++]=arr[j++];
    for(i=low,k=0;i<=high;i++,k++)//将排好序的存回arr中low到high这区间
	arr[i]=temp[k];
    delete []temp;//释放内存，由于指向的是数组，必须用delete []
}
 
  2. 希尔排序 
  class Solution{
public:
    vector shellSort(vector nums){
        int length = nums.size();
        int i, j, gap;
        for (gap = length / 2; gap > 0; gap /= 2) // 每次的增量，递减趋势
            {
                for (i = gap; i < length; i++) //每次增量下，进行几组插入排序，如第一步就是（从12，9，73，26，37）5次
                    for (j = i ; j -gap >= 0 && nums[j-gap] > nums[j]; j -= gap)// 每个元素组中进行直接插入排序，看例子
                        swap(nums[j-gap], nums[j]); //如果增量为2时他的插入查询操作下标为：
                                            //（2-0，3-1/ 4-2-0，5-3-1/ 6-4-2-0，7-5-3-1/ 8-6-4-2-0，9-7-5-3-1）
                for(int k=0; k
 
  3. 快排 
  class SolutionRepeat{
public:
    void quikSortMain(vector &datas){
        int start = 0;
        int end = datas.size()-1;
        quickSort(datas, start, end);
    }
    void quickSort(vector &datas, int start, int end){
        if (start < end)
        {
            int splitIndex = getSplitIndex(datas, start, end);
            quickSort(datas, start, splitIndex-1);
            quickSort(datas, splitIndex+1, end);
        }     
    }

    int getSplitIndex(vector &datas, int start, int end){
        int randomNum = datas[start];
        int left = start+1;
        int right = end;
        
        while (left <= right)
        {
            while (datas[left] <= randomNum && left <= right) left++;
            while (datas[right] >= randomNum && left <= right) right--;
            if(right < left){
                break;
            }
            else{
                int temp = datas[left];
                datas[left] = datas[right];
                datas[right] = temp;
            }
        }
        int temp = datas[start];
        datas[start] = datas[right];
        datas[right] = temp;
        return right;
    }
};
 
  4. 堆排序 
  #include 
#include 
#include 
using namespace std;
 
void HeapAdjust (int data[], int length, int k)
{
	int tmp = data[k];
	int i=2*k+1;
	while (idata[i+1]) //选取最小的结点位置
			++i;
		if (tmp < data[i]) //不用交换
			break;
		data[k] = data[i]; //交换值
		k = i; //继续查找
		i = 2*k+1;
	}
	data[k] = tmp;
}
 
void HeapSort (int data[], int length)
{
	if (data == NULL || length <= 0)
		return;
	for (int i=length/2-1; i>=0; --i) {
		HeapAdjust(data, length, i); //从第二层开始建堆
	}
 
	for (int i=length-1; i>=0; --i) {
		std::swap(data[0], data[i]);
		HeapAdjust(data, i, 0); //从顶点开始建堆, 忽略最后一个
	}
	return;
}
 
int main (void)
{
	int data[] = {49, 38, 65, 97, 76, 13, 27, 49};
	int length = 8;
	HeapSort(data, length);
	for (int i=0; i
 
  5. 链表的增删查改 
  场景题 
   
    
    海量文本的处理问题 
    
   
  1. 10亿个数，内存只有1M，如何让这10亿个数有序 
  tensorflow的基础知识 
  反向传播机制的工作原理