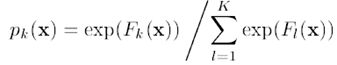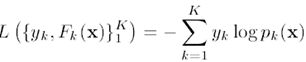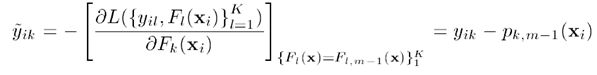Gradient Boost Decision Tree:
GBDT是一个应用很广泛的算法,可以用来做分类、回归。在很多的数据上都有不错的效果。GBDT这个算法还有一些其他的名字,比如说MART(Multiple Additive Regression Tree),GBRT(Gradient Boost Regression Tree),Tree Net等,其实它们都是一个东西(参考自wikipedia – Gradient Boosting),发明者是Friedman
Gradient Boost其实是一个框架,里面可以套入很多不同的算法,可以参考一下机器学习与数学(3)中的讲解。Boost是"提升"的意思,一般Boosting算法都是一个迭代的过程,每一次新的训练都是为了改进上一次的结果。
原始的Boost算法是在算法开始的时候,为每一个样本赋上一个权重值,初始的时候,大家都是一样重要的。在每一步训练中得到的模型,会使得数据点的估计有对有错,我们就在每一步结束后,增加分错的点的权重,减少分对的点的权重,这样使得某些点如果老是被分错,那么就会被“严重关注”,也就被赋上一个很高的权重。然后等进行了N次迭代(由用户指定),将会得到N个简单的分类器(basic learner),然后我们将它们组合起来(比如说可以对它们进行加权、或者让它们进行投票等),得到一个最终的模型。
而Gradient Boost与传统的Boost的区别是,每一次的计算是为了减少上一次的残差(residual),而为了消除残差,我们可以在残差减少的梯度(Gradient)方向上建立一个新的模型。所以说,在Gradient Boost中,每个新的模型的简历是为了使得之前模型的残差往梯度方向减少,与传统Boost对正确、错误的样本进行加权有着很大的区别。
在分类问题中,有一个很重要的内容叫做Multi-Class Logistic,也就是多分类的Logistic问题,它适用于那些类别数>2的问题,并且在分类结果中,样本x不是一定只属于某一个类可以得到样本x分别属于多个类的概率(也可以说样本x的估计y符合某一个几何分布),这实际上是属于Generalized Linear Model中讨论的内容,这里就先不谈了,以后有机会再用一个专门的章节去做吧。这里就用一个结论:如果一个分类问题符合几何分布,那么就可以用Logistic变换来进行之后的运算。
假设对于一个样本x,它可能属于K个分类,其估计值分别为F1(x)…FK(x),Logistic变换如下,logistic变换是一个平滑且将数据规范化(使得向量的长度为1)的过程,结果为属于类别k的概率pk(x),
对于Logistic变换后的结果,损失函数为:
其中,yk为输入的样本数据的估计值,当一个样本x属于类别k时,yk = 1,否则yk = 0。
将Logistic变换的式子带入损失函数,并且对其求导,可以得到损失函数的梯度:
上面说的比较抽象,下面举个例子:
假设输入数据x可能属于5个分类(分别为1,2,3,4,5),训练数据中,x属于类别3,则y = (0, 0, 1, 0, 0),假设模型估计得到的F(x) = (0, 0.3, 0.6, 0, 0),则经过Logistic变换后的数据p(x) = (0.16,0.21,0.29,0.16,0.16),y - p得到梯度g:(-0.16, -0.21, 0.71, -0.16, -0.16)。观察这里可以得到一个比较有意思的结论:
假设gk为样本当某一维(某一个分类)上的梯度:
gk>0时,越大表示其在这一维上的概率p(x)越应该提高,比如说上面的第三维的概率为0.29,就应该提高,属于应该往“正确的方向”前进
越小表示这个估计越“准确”
gk<0时,越小,负得越多表示在这一维上的概率应该降低,比如说第二维0.21就应该得到降低。属于应该朝着“错误的反方向”前进
越大,负得越少表示这个估计越“不错误 ”
总的来说,对于一个样本,最理想的梯度是越接近0的梯度。所以,我们要能够让函数的估计值能够使得梯度往反方向移动(>0的维度上,往负方向移动,<0的维度上,往正方向移动)最终使得梯度尽量=0),并且该算法在会严重关注那些梯度比较大的样本,跟Boost的意思类似。
得到梯度之后,就是如何让梯度减少了。这里是用的一个迭代+决策树的方法,当初始化的时候,随便给出一个估计函数F(x)(可以让F(x)是一个随机的值,也可以让F(x)=0),然后之后每迭代一步就根据当前每一个样本的梯度的情况,建立一棵决策树。就让函数往梯度的反方向前进,最终使得迭代N步后,梯度越小。
这里建立的决策树和普通的决策树不太一样,首先,这个决策树是一个叶子节点数J固定的,当生成了J个节点后,就不再生成新的节点了。
算法的流程如下:(参考自treeBoost论文)
0. 表示给定一个初始值
1. 表示建立M棵决策树(迭代M次)
2. 表示对函数估计值F(x)进行Logistic变换
3. 表示对于K个分类进行下面的操作(其实这个for循环也可以理解为向量的操作,每一个样本点xi都对应了K种可能的分类yi,所以yi, F(xi), p(xi)都是一个K维的向量,这样或许容易理解一点)
4. 表示求得残差减少的梯度方向
5. 表示根据每一个样本点x,与其残差减少的梯度方向,得到一棵由J个叶子节点组成的决策树
6.为当决策树建立完成后,通过这个公式,可以得到每一个叶子节点的增益(这个增益在预测的时候用的)
每个增益的组成其实也是一个K维的向量,表示如果在决策树预测的过程中,如果某一个样本点掉入了这个叶子节点,则其对应的K个分类的值是多少。比如说,GBDT得到了三棵决策树,一个样本点在预测的时候,也会掉入3个叶子节点上,其增益分别为(假设为3分类的问题):
(0.5, 0.8, 0.1), (0.2, 0.6, 0.3), (0.4, 0.3, 0.3),那么这样最终得到的分类为第二个,因为选择分类2的决策树是最多的。
7. 的意思为,将当前得到的决策树与之前的那些决策树合并起来,作为新的一个模型(跟6中所举的例子差不多)
文章来源链接:http://www.cnblogs.com/leftnoteasy/archive/2011/03/07/random-forest-and-gbdt.html