T-EDGE: Temporal WEighted MultiDiGraph Embedding for Ethereum Transaction Network Analysis （Applica）

期刊：
作者：Jiajing Wu, Dan Lin , Zibin Zheng and Qi Yuan
单位：Sun Yat-sen University
联系方式：[email protected]

---

Abstract

近来，图嵌入技术已被广泛用于各种网络的分析中，但是大多数现有的嵌入方法都忽略了可能在金融交易网络中起作用的边缘的时间和加权信息。以太坊的开放性为我们提供了该领域前所未有的数据挖掘机会。考虑到交易网络的现实规则和特征，我们建议将以太坊交易网络建模为时间加权多重图（TWMDG），其中每个节点都是唯一的以太坊账户，每个边代表按金额加权并分配时间戳的交易。在TWMDG中，我们通过结合边缘的时间和加权信息来定义时间加权多图嵌入（T-EDGE）问题，目的是捕获动态交易网络的更全面的属性。为了评估所提出的嵌入方法的有效性，我们对从以太坊收集的真实交易数据进行了预测任务的实验，包括时间链接预测和节点分类。实验结果表明，T-EDGE的性能优于其他嵌入方法，这表明与时间有关的walk和edge的多重性对于信息灵敏的交易网络是重要的。

1.Introduction

关于金融交易网络的分析研究相对较少，因为出于安全和利益的考虑，交易数据通常是私有的。区块链数据的开放性为研究人员提供了该领域数据挖掘的前所未有的机会。
作为支持智能合约的最大的基于公共区块链的平台，以太坊受到广泛关注，为了促进智能合约的实施，以太坊引入了账户的概念，这实际是一个地址，但增加了存储空间来记录账户余额，交易，代码等。以太坊上相应的加密货币称为以太币，可以在账户之间转移并用于补偿参与者挖矿节点。自2014年首次亮相以来，以太坊已经积累了大量的用户交易记录。利用这些记录，Chen等人进行了第一个系统的研究，以表征以太坊并通过传统的网络分析获得新的观察结果。与其他大型复杂网络，以太坊交易网络不同， 每个边缘代表一个特定的以太币交易，其中包含一些唯一的信息，例如交易的方向，金额值和时间戳。本文，我们将以太坊交易网络建模为时间加权多重图，其中节点是唯一地址，边代表按金额加权并分配了时间戳的交易。
图嵌入是一种用于在低维空间中表示节点特征的有效方法，用于网络分析和下游机器学习任务。在各种图嵌入方法中，已提出了一系列基于随机游走的方法，以通过最大化相邻节点共现的可能性来学习从原始图到低维向量空间的映射函数。
结合以太坊等交易网络的现实规则和特征，交易网络嵌入的挑战如下：
（1）随着时间的推移，交易网络随着链接的增加而不断发展，这在大多数现有的图嵌入算法中都被忽略了；
（2）帐户之间的联系的实际含义不是一次性建立的关系，而是与时间有关的事件，因此，在交易网络嵌入中需要考虑多个边缘；
（3）与社交网络不同，在以太坊交易网络上的随机游走是具体的，代表了现实世界中的汇款流量；
（4）交易金额在一定程度上反映了两个账户之间的相似性。在大多数情况下，交易额越大，两个帐户之间的关系越紧密。
为此，我们提出了一个新颖的框架，称为时间加权多重图嵌入（T-EDGE），旨在捕获时间敏感交易网络的不可忽略的时间属性和重要的汇款趋势。对于此处讨论的交易网络，忽略时间信息的现有方法可能会采样大量无效交易。
如图所示，按照传统采样，{A5，A1，A2}是可能的随机游走序列，但是，在时间图中它是不切实际的，因为从A1到A2发生得较早。在CTDNE中，尽管考虑了时间信息，但忽略了点之间多个边的存在。例如，根据CTDNE，{A0，A1}，下一次游走到A2取决于交易路径1或3。
这种时序游走代表了交易网络中资金流动的实际可行路径。因此，预期所提出的方法将学习更多有意义且准确的时间相关节点嵌入，这些嵌入可从动态交易网络中捕获更全面的属性。

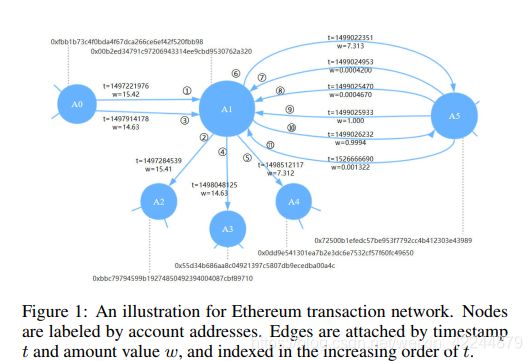
本文的主要贡献如下：
（1）据我们所知，这是首次通过图嵌入了解以太坊交易记录。特别地，我们考虑了两个重要且实用的机器学习任务，即链接预测和节点分类；
（2）我们通过考虑时间相关性和边的多样性来完善交易网络的时序游走的定义，这种随机游动序列包含交易网络中资金流的实际含义；
（3）我们提出了一种新颖的图嵌入方法，称为时间加权多重图嵌入（T-EDGE），该方法结合了时域和金额域中的交易信息，并且对真实的以太坊数据进行的实验证明了其优于现有方法的优势 。

2.Framework

2.1 Network Construction

Given a graph G = (V, E), each edge is unique and is represented as e = (u, v, w, t), where u is the source node, v is the target node, w is the weight value and t is the timestamp.

2.2 Temporal Weighted Multidigraph Embedding

第一部分是随机游走，它在时间约束和灵活的有偏策略下进行游走采样。
第二部分是基于SkipGram的更新过程，学习节点的向量表示。
Temporal Walk（时序游走）：游走节点时，序列是时间非递减的。
如果存在从u到v的时序路径，我们定义节点u和v是连接的。

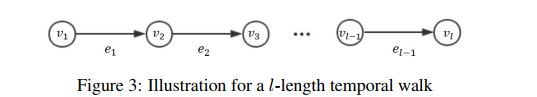
Temporal Successive Edges（时序直达边）：给定当前时间戳t和节点u，穷尽节点u所有可能直接游走的时序边（交易时间>=t)。（表示给定时间t，节点u所有可以直达的点）

构建了交易网络，定义了直接连接边的定义之后，我们定义有偏和无偏的采样策略。
从时域的角度来看，采样策略如下：
无偏：
TUS——每个直达点被采的概率相等，个数分之一。

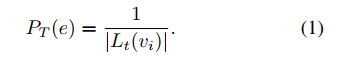
有偏：
TBS（1）——对这些时序边按照交易时间进行降序排列，分子是每个节点的位次，分母是总的位次和，即离给定时间t越近的交易被采样的概率越大。

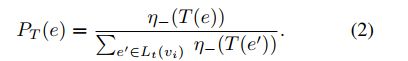
TBS（2）——反之，另一种策略是对这些时序边按照交易时间进行升序排列，分子是每个节点的位次，分母是总的位次和，即离给定时间t越近的交易被采样的概率越小。

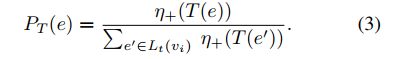
从边权–交易金额的角度来看，采样策略如下：
无偏：
WUS——每个直达点被采的概率相等，个数分之一。

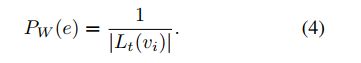
有偏：
WBS（1）——对这些时序边按照交易金额大小区分，分子是该笔交易金额，分母是u和这些直达点总的交易金额和，交易金额越大，被采样的概率越大。

WBS（2）——对这些时序边按照交易金额进行升序排列，分子是每个节点的位次，分母是总的位次和，避免金额比较小的交易被采样的概率太小。

最后，我们结合时间和权重域（即PT和PW）中的上述采样概率
确定采样策略以后，根据W2V最大化邻居节点出现的概率学习节点表示即可。

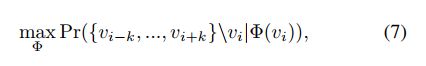
3.Experiments on Ethereum

3.1 Data Collection

由于处理具有超过200万个EOA的整个以太坊交易网络非常耗时，因此在此我们确定了许多目标账户，以每个目标为中心，我们获得有向K阶子图，K-in和K-out是采样的超参数。这里的采样是对全局网络采样一部分出来进行分析。

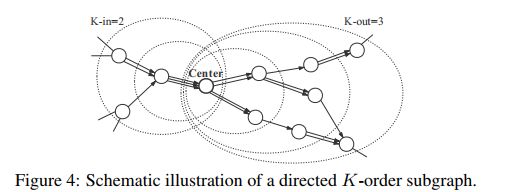
3.2 Link Prediction

首先，按照时间对所有交易进行排序，找到时间相对较早的交易E’，作为已知边，G=（V,E’），进而采样进行节点特征学习；（没有解释较早交易的定义）
然后，预测link验证节点学习的特征，将E’内的node pair 作为正样本，随机采样相同数量的没有link的node pair 作为负样本，将节点对向量串联拼接成新的样本作为输入，输出即是二分类，学习分类器；
最后，在测试集上对分类器性能进行验证，测试集中timestamp较大的link实际label标记为1.（有无连接作为1,0的区分？）
Dataset：文章采样三个交易网络，选定中心点确定K-in和K-out采集数据集
Settings：选择DeepWalk和N2V作为比较基准，设置d=128，k=4；对三个网络分别设置r=20,l=10；r=10,l=10；r=10,l=20；N2V使用网络搜索p,q={0.5,1,1.5,2.0}.
Discussion of results：文章在link预测上进行了三个部分的试验，循序渐进，首先是方法比较，而后是参数敏感性试验，最后是采样的无偏和有偏性比较。
第一部分：
T-EDGE是采样时采用无偏策略，每个可能的有效边被采样的概率相等；T-EDGE（TBS+WBS）表示采用有偏策略，TBS和WBS两两组合共计四种情况，表中列出的是最好的结果。

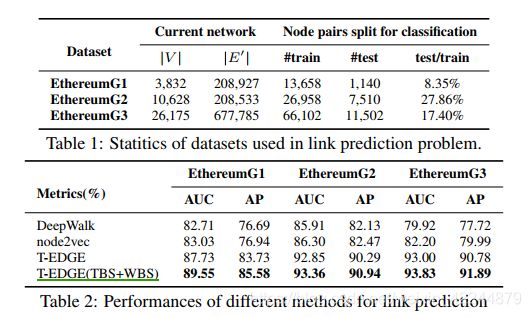
结果表明：
（1）T-EDGE无偏采样比传统图嵌入算法都好，这表明，考虑时间信息以及边缘的多重性特征对于金融交易网络的分析和理解非常重要且有意义。
（2）在有偏采样的情况下，T-EDGE（TBS + WBS）的性能要比无偏T-EDGE更好，这表明时域和量域中的丰富信息确实有助于我们获得更全面的表示性预测任务。
第二部分：
为了进一步证明T-EDGE的优越性，文章在一个网络上进行试验改变参数的设置。

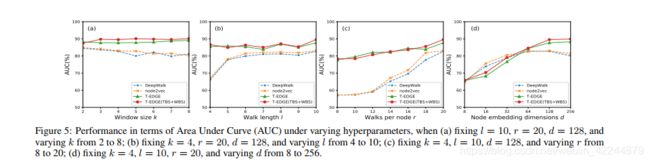
结果表明：
（1）在k，l，r的不同情况下，带有或不带有附加偏置的T-EDGE始终优于DeepWalk和node2vec；
（2）DeepWalk和node2vec对两个超参数（步长l和每个节点的步长r）更敏感，而T-EDGE相对比较稳健；
（3）随着d的增加，T-EDGE方法的性能会单调提高，但DeepWalk和node2vec的性能会随着d大于64而下降，这意味着T-EDGE方法可以嵌入更丰富的有用信息。
第三部分：
为了进一步研究不同采样策略对T-EDGE方法的影响，文章对时间和权重采样策略进行两两组合，结果如下：

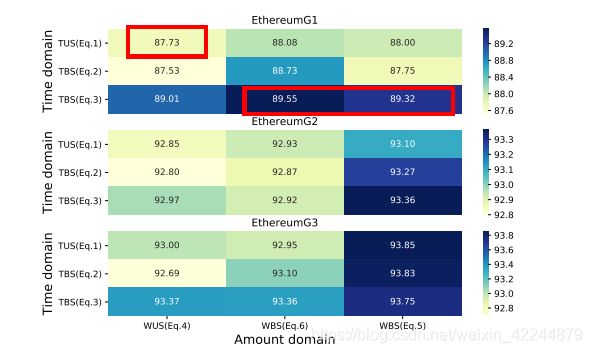
结果表明：
有偏方法优于无偏方法；
考虑时间和权重的有偏采样比仅考虑时间或仅考虑权重的采样方法要好。

3.3 Node Classification

网络钓鱼诈骗是一种新型的网络犯罪，它随着在线业务的出现而出现。
据报道，自2017年以来，它占以太坊所有网络犯罪的50％以上。
（补充：网络钓鱼 （Phishing）攻击者利用欺骗性的电子邮件和伪造的 Web 站点来进行网络诈骗活动，受骗者往往会泄露自己的私人资料，如信用卡号、银行卡账户、身份证号等内容。诈骗者通常会将自己伪装成网络银行、在线零售商和信用卡公司等可信的品牌，骗取用户的私人信息。）
为了进一步评估提出的T-EDGE策略的性能，我们还在以太坊上进行了节点分类实验，对标记的网络钓鱼节点和未标记的节点（视为非网络钓鱼节点）进行分类。我们考虑了445个标记的网络钓鱼节点以及与我们的目标节点相同数量的随机选择的未标记节点。
假设对于典型的以网络钓鱼节点为中心的以太传输流，网络钓鱼节点的前一个节点可能是受害者，而后一个节点到三个节点可能是具有洗钱行为的桥梁节点。（待解释）
文章的试验部分为890个目标节点中的每一个节点收集了K-in = 1，K-out = 3的子图，然后将它们拼接成具有86,623个节点的大规模网络。试验参数设置k=4,r=4,l=10,d=128,分别在不同比例的数据集上进行训练，这些结果进一步验证了我们的假设，即通过考虑时间属性和汇款信息，我们可以获得交易网络的更有意义的表示形式，可以有效地提高预测性能。

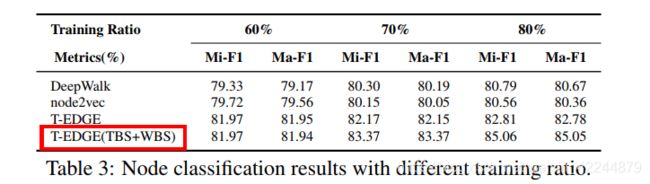
4.Conclusion

文章提出了一种通过网络嵌入进行以太坊分析的新颖框架，构造了一个时间加权多重图以尽可能保留信息，并提出了一种称为T-EDGE的图嵌入方法，该方法将金融交易网络的时间和加权信息合并到节点嵌入中。
我们在现实的以太坊网络上实现了嵌入方法，以实现两个与实际相关的预测任务，即时间链接预测和网络钓鱼/非网络钓鱼节点分类。实验结果证明了所提出的T-EDGE嵌入方法的有效性，同时表明时间加权多重图可以更全面地表示动态交易网络的时间和汇款属性。对于未来的工作，我们可以使用建议的嵌入方法来研究以太坊的更多应用，或者扩展当前框架来分析其他大规模的时域或领域相关网络。