《异常检测——从经典算法到深度学习》6 基于重构概率的 VAE 异常检测

《异常检测——从经典算法到深度学习》

• 0 概论
• 1 基于隔离森林的异常检测算法
• 2 基于LOF的异常检测算法
• 3 基于One-Class SVM的异常检测算法
• 4 基于高斯概率密度异常检测算法
• 5 Opprentice——异常检测经典算法最终篇
• 6 基于重构概率的 VAE 异常检测
• 7 基于条件VAE异常检测
• 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
• 9 异常检测资料汇总（持续更新&抛砖引玉）
• 10 基于条件 VAE 的鲁棒无监督KPI异常检测
• 11 针对大量出现的KPI流快速部署异常检测模型

相关：

VAE 模型基本原理简单介绍

6. 基于重构概率的 VAE 异常检测

论文名称：Variational Autoencoder based Anomaly Detection using Reconstruction Probability
发表时间：2015.12 立即下载
[1] An, Jinwon, and Sungzoon Cho. “Variational autoencoder based anomaly detection using reconstruction probability.” Special Lecture on IE 2.1 (2015): 1-18.

论文总体结构为：
Abstract: 我们提出了一种基于重构概率的异常检测方法
可变自动编码器。

1. Introduction
2. Backgroud
   2.1 Anomaly detection：介绍异常检常用几个方法。
   2.2 Autoencoder and anomaly detection: 介绍自编码器(autoencoder) 如何进行异常检测。
   2.3 Variational Autoencoder：介绍 VAE 的核心内容、VAE 与 AE 的区别 以及 VAE 训练算法。
3. Proposed method
   3.1 Algorithm： 总体介绍基于 VAE 模型的异常检测算法。
   3.2 Reconstruction Probability：介绍上述算法中用的 reconstruction probability。
   3.3 Difference from an autoencoder based anomaly detection： 介绍两种算法的区别。
4. Experimental Results
   实验部分用到了两个数据集 KDD cup 1999 与 MNIST，并与其他算法进行的比较。

接下来会对各部分进行介绍，请根据需要进行查看。

6.1 Introduction

内容包括：

• 三两句介绍异常的定义、异常检测的意义。

• 从光谱异常检测技术中引出基于重构误差的检测方法，并指出基于 PCA 的方法属于这种方法。

• 从降维的角度引出自编码器(Autoencoder)，并说明这样的好处：更好提取特征、更高的隐藏层能够获取一些抽象特征。

• 提出基于 VAE 的异常检测算法，并说明其优点：与自动编码器和PCA相比，VAE的优势在于它提供了一个概率度量，而不是作为异常分数的重建误差，我们称之为重建概率。概率比重建误差更具原则性和客观性，不需要模型特定的阈值来判断异常。

  可以用在自己论文中
  Hawkins defined an anomaly as an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism[5].

6.2 Background

6.2.1 Anomaly detection

异常检测方法总的分类：

• 统计异常检测假设数据是从指定的概率分布建模的。参数模型（如高斯混合模型）或非参数模型（如核密度估计）可用于定义概率分布。如果从模型中生成数据点的概率低于某个阈值，则将其定义为异常。这种模型的优点是给出了概率作为判断异常的决策规则，具有客观和理论上的合理性。
• 基于邻近度的异常检测假设异常数据与大多数数据隔离。用这种方法对异常进行建模有三种方法，即基于聚类的、基于密度的和基于距离的。对于基于聚类的异常检测，将聚类算法应用于数据，以识别数据中存在的密集区域或簇。对每一个异常点的关系进行评估，形成每一个异常点的关系。这些标准包括到星团质心的距离和最近的星团的大小。如果到簇质心的距离高于阈值或最近的簇的大小低于阈值，则数据点被定义为异常。基于密度的异常检测将异常定义为位于数据稀疏区域的数据点。例如，如果数据点的局部区域内的数据点数量低于阈值，则将其定义为异常。基于距离的异常检测使用与给定数据点的相邻数据点相关的测量。K近邻距离可用于这样一种情况，即具有较大K近邻距离的数据点被定义为异常。
• 基于偏差的异常检测主要基于光谱异常检测，以重建误差作为异常分数。第一步是使用降维方法（如主成分分析或自动编码器）重建数据。利用k-最显著主成分对输入进行重构，并测量其原始数据点与重构数据点的差值，从而产生重构误差，作为异常评分。将重建误差较大的数据点定义为异常。

6.2.2 Autoencoder and anomaly detection

• Autoencoder 是通过无监督训练得到的网络，包括编码 (encoder) 和解码(decoder) 两部分。encoder 过程对应公式 (1) ，decoder 过程对应公式 (2)，而公式 (3) 用于结算编码与解码过程对应原始数据造成的误差。称为重构误差(reconstruction error)，训练的目的就是最小化重构误差。
  $$h=\sigma (W_{xh}x+b_{xh})(1)$$

  $$z=\sigma (W_{hx}h+b_{h}x)(2)$$

  $$||x-z||(3)$$

• 其中的 $h$ 称为隐藏层，隐藏层的维度比输入层低，decoder 过程需要根据 $h$ 重现输入数据 $x$ 。这使得自动编码器对具有白噪声的数据具有鲁棒性，并且只捕获数据的有意义的模式。
  自编码器的训练算法大致如下：
  

• 基于 AE 的异常检测是一种基于偏差的半监督学习算法，把重构误差 (reconstruction error) 作为异常值（anomaly score）。只把正常数据投入训练，完成训练后再对数据进行编码和解码操作，如果解码后数据与原始数据相近的数据是正常数据；当某数据的重构误差值高，我们认为是异常数据。
  基于 AE 的异常检测算法如下：
  

  可以用在自己论文中
  Anomaly detection methods can be broadly categorized in to statistical, proximity based, and deviation based [1].

6.2.3 Variational Autoencoder

VAE 模型公式推导、更多介绍推荐参考 VAE 模型基本原理简单介绍

• 变分自动编码器（VAE）是一种有向概率图形模型（DPGM），其后验由神经网络逼近，结构类似于自动编码器。如图一所示 ：
  编码与解码过程如图二所示：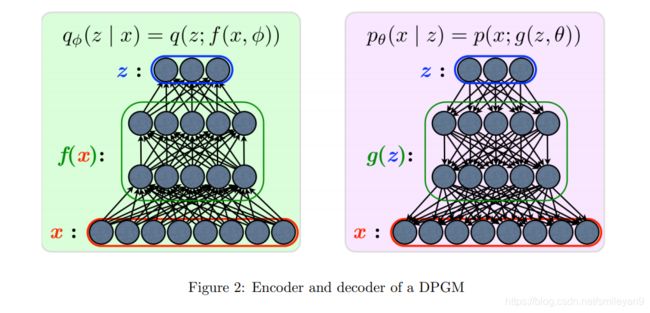
  编码与解码过程分别交给两个神经网络完成，VAE 的整体结构如图三所示：
  
  关于 VAE 更详细的介绍推荐参考 VAE 模型基本原理简单介绍
• VAE和自动编码器之间的主要区别是，VAE是一个随机生成模型，可以提供校准的概率，而自动编码器是一个确定性的判别模型，没有概率基础。这一点很明显，因为VAE对上述分布的参数进行了建模。
• VAE 模型的训练算法如图所示
  

6.3 Proposed method

6.3.1 Algorithm

请务必结合上图理解下面的算法步骤：

• 使用正常数据进行训练，训练过程中 decoder 和 encoder 共同确定隐变量的参数（即多个正态分布的$\sigma$ 和 $\mu$）。对应图片中的
  $\varphi ,\theta \leftarrow$ train a variational autoencoder using the normal dataset X
• 对于N个测试数据循环遍历，对于每个测试数据 $x^i$ 操作如下：
  • 对于每个测试数据 $x^i$，通过训练好的 VAE 模型得到 ${\mu }_z(i)$ 和 ${\sigma }_z(i)$。
  • 根据刚刚得到 ${\mu }_z(i)$ 和 ${\sigma }_z(i)$ 得到关于z的正态分布$N({\mu }_z(i),{\sigma }_z(i))$ ，从中抽取样本 L。
  • 对于抽取样本L中的每一个数据 $z^{(i,l)}$，关于 $l$ 的循环：
    • 进行 decode 操作，得到 $\hat{x}$，这里可能是为了表示 $\mu (l)$、$\sigma (l)$ 与 $\hat{x}(i)$ 的关系，记作 ${\mu }_{\hat{x}}(i,l)$ 和 ${\sigma }_{\hat{x}}(i,l)$
    • 循环结束后得到多个 ${\mu }_{\hat{x}}(i,l)$ 和 ${\sigma }_{\hat{x}}(i,l)$. 其实就是多个 $\hat{x}$
  • 通过多个 ${\hat{x}}_i$ 与训练好的 VAE 模型生成原来的测试数据 $x_i$，并计算重构概率（reconstruction probability）。
  • 这里计算的重构概率是对 $E_{q_{\phi }(z|x)}[log{p}_{\theta }(x|z)]$ 的 蒙特卡罗估计(Monte Carlo
    estimate)，当数据的重构概率很高时被归类为异常。

6.3.2 Reconstruction Probability

重构概率的计算公式在上图中（Algrithm 4）给出，这里特地摘出来方便编码：
$$reconstructionprobability(i)=\frac{1}{L}\sum _{l=1}^L{p}_{\theta }(x^{(i)}|{\mu }_{{\hat{x}}^{(i,l)}},{\sigma }_{{\hat{x}}^{(i,l)}})$$

• 重构概率(reconstruction probability) 由随机隐变量计算，这些隐变量可以输出原始输入变量分布的参数，而不是输入数据本身。（注： 然后使用这些参数和生成网络生成数据，所以说，不是重构输入数据本身）从本质上讲，这是从后验分布中提取的确定的隐变量生成数据的概率。由于从隐变量分布中提取了大量样本，这使得重构概率能够考虑隐变量空间的可变性，这是该方法与基于自动编码器的异常检测方法的主要区别之一。可以使用适合数据的输入变量空间的其他分布。
• 对于连续数据，正态分布可以用在算法4中。对于二进制数据，可以使用伯努利分布。在隐变量空间分布的情况下，一个简单的连续分布，如各向同性正态分布是首选。这可以通过谱异常检测的假设来证明，隐变量空间比输入变量空间简单得多。

6.3.3 Difference from an autoencoder based anomaly detection

VAE的重构概率与自动编码器的重构误差不同之处包括：

• 隐变量是随机变量。AE的隐变量由确定性映射定义，但 VAE 使用概率编码器来模拟隐变量的分布，而不是隐变量本身，因此可以从采样过程中考虑隐变量空间的可变性。VAE 相对 AE 而言扩展了表达能力，因为即使正常数据和异常数据可能共享相同的平均值，可变性也可能不同。据推测，异常数据的方差较大，重构概率较低。由于 AE 的确定性映射可以看作是到 $\delta$ 分布平均值的映射，所以 AE 缺乏处理变化的能力。（通俗来说讲，AE 太实诚了，不懂得变通）
• 重构的是随机变量。重构概率不仅考虑了重构与原始输入的差异，而且考虑了分布函数的方差参数对重构结果的影响。这一特性使得对根据变量方差重构的选择性敏感。方差较大的变量可以容忍重构过程中与原始数据之间的较大差异，而方差较小的变量将显著降低重构概率。这也是 AE 由于其确定性映射关系缺少的特性。
• 重构是概率度量。基于 AE 的异常检测使用重构误差作为异常值，如果输入变量是异构的，则很难计算出异常值。为了总结异构数据的差异，需要加权求和。但没有一种通用的客观方法来确定合适的权重，因为权重会因数据而异。而且，即使在权值确定之后，确定重构误差的阈值也很麻烦。没有明确的客观门槛。相比之下，重构概率的计算不需要对异构数据的重建误差进行加权，因为每个变量的概率分布允许它们根据自身的可变性分别计算。对于任何数据，1% 的概率总是 1%。因此，与重构误差阈值的确定相比，重构误差阈值的确定更为客观、合理、易于理解。

6.4 Experimental Results

6.4.1 Datasets and setup

论文用到两个数据集，使用方法如下：

• KDD cup 1999：将数据按 80% 与 20% 的比重分为正常数据与异常数据，训练时用到其中的正常数据。KDD 元数据包含五类数据，如下图 (Table 1) 所示。预处理时对于分类用到了 one-hot 方法，对于数值变量，采用0均值标准化和单位方差处理。
• MNIST：把某个数字对应的数据作为异常，而其他9个数字作为正常数据。（比如说假设1为异常数据局而其他9个数字对应的数据都为正常数据）
  

可以用在自己论文中
Datasets used for anomaly detection are MNIST dataset [9] and KDD cup 1999 network intrusion dataset (KDD) [6].

6.4.2 Model setup

对于两个数据集，

• VAE 模型的 Encoder 和 Decoder 分别对应一个隐藏层，并且维度为 400。中间的隐变量的维度为200。VAE 使用 reconstruction probability 作为异常值。
• AE 使用两个隐藏层分别用于 Encoder 和 Decoder 维度分别为 400,200.
• linear PCA 和 kernel PCA (kPCA) with a Gausssian kernel 。

6.4.3 Performance evaluation

性能评估方法：

• AUC-ROC (Area under the curve of the receiver operating characteristic )
• AUC-PRC (average precision
  or Area under the curve of the precision recall curve)
• f1-score

6.5 Conclusion

总结全文：提出了一种使用 VAE 进行异常检测的算法，这种算法是通过计算给定数据的重构概率来判断这个数据的异常成都。并且与AE、PCA、kPCA 算法进行的对比，结果显示 VAE 的优于其他三种算法。

6.6 代码实现

结束了论文阅读后就到了编码实验部分了，这篇 2015 年的论文实验讲道理应该不难实现，推荐参考对应的实现（注：不是论文作者），地址如下：

• https://github.com/Michedev/VAE_anomaly_detection
• https://github.com/SchindlerLiang/VAE-for-Anomaly-Detection

主要问题包括

• 使用tensorflow 1.x 实现
• 没有关于 PCA、kPCA、AE 等的实现

如果有任何疑问请评论，讨论一下解决问题。

6.7 重构概率计算

以下代码摘录于： https://github.com/Michedev/VAE_anomaly_detection
并且对该代码进行简单的分析：

from scipy.stats import multivariate_normal

def reconstructed_probability(self, X, L=100):
    """
    X 即需要计算重构概率的一组数据。
    以 MNIST 为例，如果每次测 32 条数据，那么 X.shape = (32,28,28)
    """
    # 初始化每个待测数据的概率为 0 
    reconstructed_prob = np.zeros((X.shape[0],), dtype='float32')
    
    # 从模型中拿到均值和方差，注意 均值和方差都是数列
    mu_hat, sigma_hat = self.session.run([self.mu_post, self.sigma_post], {
     self.X: X})
    
    # 进行 L 次采样
    for l in range(L):
        mu_hat = mu_hat.reshape(X.shape)
        sigma_hat = sigma_hat.reshape(X.shape) + 0.00001
        
        # 计算每个测试数据的重构概率
        for i in range(X.shape[0]):
            p_l = multivariate_normal.pdf(X[i, :], mu_hat[i, :], np.diag(sigma_hat[i, :])) 
            reconstructed_prob[i] += p_l

    # 取平均值
    reconstructed_prob /= L
    return reconstructed_prob

注意 multivariate_normal 来自于 scipy.stats，并且根据协方差矩阵的性质而传入方差从而计算概率密度。

注意： 经过编码实践发现改代码存在一个重大的问题——正确率与 L 大小无关。

很明显这个与论文原来的设计思想是不一致的。再看论文算法截图，注意其中部分

for l=1 to L do
   ...这一行内容
end for

即 ${\mu }_{{\hat{x}}^{(i,l)}},{\sigma }_{{\hat{x}}^{(}i,l)}=g_{\varphi }(x|z^{(}i,l))$ 这行的理解。

按照上面摘录的代码，对于每一份测试数据只对应一份隐变量 $z$，也就是说，对每个测试数据其实只经历过一次 encode 得到 $\mu$ 和 $\sigma$ ，然后再进行pdf 计算等等，重复 L次。

然后 L 次计算一模一样，参数一样，数据一样，结果也一样。也就是说，对于上面那份源码 L=100 与 L=10 的结果是一模一样的。感兴趣的伙伴可以测试一下。

解决方法
算法的本意应该是，根据每个输入数据 $x_i$ 对应的 $\mu$ 和 $\sigma$ 可以得到一个 $z$ 的分布（注意可以是多元高斯分布），然后再从这个分布中采样 $L$ 次，得到 $L$ 组 $\hat{\mu }$ 与 $\hat{\sigma }$ 然后再计算分别计算概率密度（即输入数据$X$ 在这 $L$ 组中的概率密度），再求均值。

为了方便可以考虑 去掉 L 次循环，就执行一次就好了。（注：这个地方很值得讨论一下）

6.8 总结

这篇论文介绍的是使用 reconstruction probability 作为异常值，基本思想就是在一个首先构建一个生产正常值的环境 (即由隐变量所确定的隐变量空间），在这个环境中不管如何 sample 拿到的可能与输入数据差别很大，但是这种差别依然是在正常数据的容忍范围内。但是如果不在这个环境中sample 而是投入另外一组异常特征，生成数据与正常数据差异就很大。也就是reconstruction probability 的值很大，我们觉得它与正常数据差别很大，它不属于这个优雅的环境，所以判定它为异常数据。

Smileyan
2020.10.24 15:36
最后更新：2021.1.7 21:14

感谢您的 点赞、 收藏、评论 与 关注