SPPNET 经典论文【论文笔记 + pytorch实现】
Contents
-
- 0 摘要
- 1 Intorduction
- 2 基于空间金字塔池化的深度网络
-
- 2.1 卷积层和特征图
- 2.2 空间金字塔池化层
- 2.3 训练网络
- 3 用于图像分类的SPP-NET
-
- 3.1 ImageNet 2012分类实验
- 3.2 Experiments on VOC 2007 Classification
- 3.3 Experiments on Caltech101
- 4 用于目标检测的SPP-NET
- 5 总结
- 6 pyTorch实现SPP层
0 摘要
对于深度神经网络的输入图片尺寸必须是固定的,还记得在R-CNN网络中通过selective search选出2000个候选区域之后要使用放射图像变形的方法来对每个不同形状的region proposal产生一个固定尺寸作为CNN的输入(也就是把不同大小的候选区域 resize为相同大小),这样会使得识别的精度降低(reduce the recognition accuracy) 。在R-CNN论文出现后,首次提出AlexNet模型的作者何凯明再次提出了SPP-Net(Spatial Pyramid Pooling)来解决上述提到的问题。不管输入图像的尺寸是什么,该模型均能够产生固定大小的表示(fixed-length representation)。
通过使用SPP-Net模型,只需要从整张图片计算一次特征图(feature map),然后对任意尺寸的区域(子图像)进行特征池化,即可生成一个固定尺寸的表示用于训练检测器。
该模型在图像分类和目标识别两方面上均取得了较大的提升。
1 Intorduction
摘要中提到的resize图片主要采用的两种方法为裁剪(crop) 和扭曲(warp)(如下图所示),但裁剪会导物体信息的丢失,变形会导致位置信息的扭曲,从而影响识别的精度。

作者分析,卷积神经网络是有卷积层和全连接层组成的,其中只有全连接层需要固定尺寸的输入,为什么呢?
对于全连接层的计算z=wx+b,其实相当于输入的特征图数据矩阵x和全连接层权值矩阵w进行内积,在配置一个网络时,全连接层的参数维度是固定的,所以要想两个矩阵能够进行内积,则输入的特征图的数据矩阵维数也需要固定。
而对于卷积层,卷积核的每个元素表示参数w,不论输入图像大小怎么改变,卷积核大小是不变的,并且通过卷积操作,每次都能训练到卷积核中的元素,所以卷积层的输入图像的大小是任意的。
加入SPP-Net前后的网络模型对比如下:

简单介绍一下Spatial Pyramid Pooling的优点:
- SPP能在输入尺寸任意的情况下产生固定大小的输出,而以前的深度网络中的滑窗池化(sliding window pooling)则不能;
- SPP使用了多层级空间箱(bin),而滑窗池化则只用了一个窗口尺寸。多级池化可以提高对于检测变形物体的鲁棒性;
- 由于SPP对输入图像尺寸的灵活性,它可以池化从各种尺度抽取出来的特征。
SPP不仅可以用在需要固定尺寸输入的全连接层中用于测试,还可以在训练阶段使用。训练时使用多种尺寸的图像可以提高缩放不变性并且减少过拟合。
作者还实现了一种多尺度训练方法。即为了实现一个能够接受各种输入尺寸的网络,在训练阶段的每个epoch,可以针对一个给定的输入尺寸进行网络训练,然后在下一个epoch,再切换到另一个尺寸。实验表明,这种多尺度训练和传统的单一尺度训练一样可以收敛,并且能达到更好的测试精度。
在R-CNN中对每张图片中的上千个候选区域反复调用CNN提取特征,而本文只需要在整张图片上运行一次卷积网络层(不关心候选区域的数量),然后再使用SPP-Net在特征图上抽取特征,这个方法比R-CNN计算特征要快24-102X 倍,并且精度也更高。
2 基于空间金字塔池化的深度网络
2.1 卷积层和特征图
下图是由第五卷积层的一些过滤器所生成的特征图,它们不仅涉及响应的强度,还包含了空间位置。特征图的生成并不需要固定的尺寸输入。

2.2 空间金字塔池化层
卷积层接受任意大小的输入,故卷积层的输出也是任意大小的,而分类器(SVM/softmax)或者全连接层需要固定的输入大小的向量。这种向量可以使用词袋方法(BoW)通过池化特征来生成。空间金字塔池化对BoW进行了改进,以便在池化过程中保留局部空间块(local spatial bins)中的空间信息。这些空间块的尺寸和图像的尺寸是成比例的,在这样的情况下块的数量就是固定的。
将AlexNet模型中第五层卷积层后的池化层替换为空间金字塔池化层(最大池化法),该层的输出是一个k×M维向量,其中M代表空间块的数量,k代表最后一层卷积层的过滤器的数量。 这个固定维度的向量就是全连接层的输入。
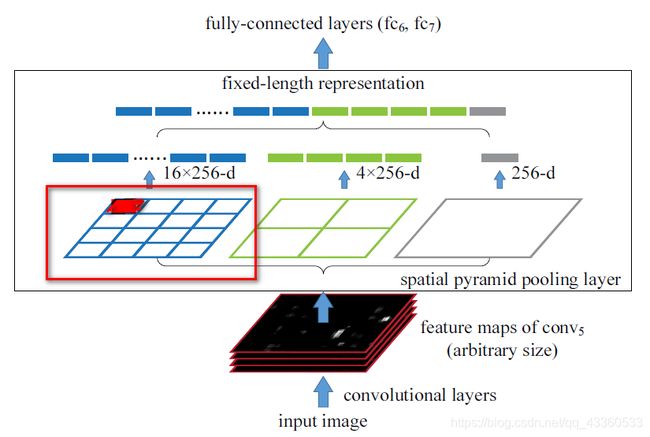
上图表示通过是4×4,2×2,1×1的块池化特征图,即将这三张网格放到下面这张特征图上,可以得到16+4+1=21种不同的块。从这21个块中,每个块提取出一个特征,这样刚好就是我们要提取的21维特征向量。这种以不同的大小格子的组合方式来池化的过程就是空间金字塔池化(SPP)。例如上图中,Conv5计算出的feature map是任意大小的,经过SPP之后,共输出(16+4+1)×256的特征。(有256个卷积核)
2.3 训练网络
- 单尺度训练:首先使用固定尺寸的图像大小224×224作为输入。对于给定尺寸的图像,先计算空间金字塔池化所需要的块(bins)的大小。假设一个conv5之后特征图尺寸大小为
a×a,那么对于n x n块的金字塔级,我们实现一个滑窗池化过程,窗口大小为win = 上取整[a/n],步幅stride = 下取整[a/n]。对于L层金字塔,我们实现L个这样的层,然后将L个层的输出进行连接,输出给全连接层。单一尺寸训练的主要目的是使能多层级的池化表现。 - 多尺度训练:考虑这两个尺寸:180×180、224×224,使用缩放(resize)将224×224的图像尺寸所缩放为180×180的大小。注意这样处理使得不同尺度的区域仅仅是分辨率上的不同,而不是内容和布局上的不同。 对于接受180×180输入的网络,我们实现另一个固定尺寸的网络。本例中,conv5输出的特征图尺寸是
a×a。仍然使用win = 上取整[a/n],str = 下取整[a/n],实现每个金字塔池化层。这样训练过程中,通过使用共享参数的两个固定尺寸的网络实现了不同输入尺寸的SPP-net。
多尺寸训练的主要目的是在保证已经充分利用现在被较好优化的固定尺寸网络实现的同时,模拟不同的输入尺寸。此外,上面的单尺寸或多尺寸方法只用于训练阶段。在测试阶段,直接对各种尺寸的图像应用SPP-Net。
3 用于图像分类的SPP-NET
3.1 ImageNet 2012分类实验
首先作者对于ZF-5、Convnet*-5、Overfeat-5/7三个在 ImageNet 2012 分类表现较好的模型进行简要阐释,然后通过多层次池化提升准确度(即金字塔池化层的规模不同:{6×6,3×3,2×2,1×1}、{4×4,3×3,2×2,1×1})、 多尺寸训练提升准确度(训练阶段输入不同尺寸大小的图片)、全图像表示提升准确度(仅缩放不裁剪图片)、特征图上的多视图测试来验证了SPP-Net模型的优越性。
3.2 Experiments on VOC 2007 Classification
在这次实验中,作者主要通过mAP指标指出,相对于经过调优和多角度测试的深度神经网络,在测试阶段仅仅使用全视图的SPP-Net模型在未经调优的情况下仍可以达到相对较好的结果。
3.3 Experiments on Caltech101
结合数据总结,SPP-Net模型比非SPP-Net模型表现更好,全视图比裁剪或扭曲后的视图表现更好。
4 用于目标检测的SPP-NET
R-CNN一张图像产生的2000个候选区域上反复应用深度卷积网络,而作者的方法是只在整张图像上抽取一次特征。然后在每个特征图的候选窗口上应用空间金字塔池化,输出一个固定长度的向量。因为只应用一次卷积网络,相比于R-CNN快得多。
SPP-Net在特征图中直接抽取特征,而R-CNN则要从图像区域抽取。
对于SPP-Net网络,首先对于输入图片进行一次卷积获取整张图的特征,然后对于2000个候选区域进行空间金字塔池化({6×6,3×3,2×2,1×1}),最后对于每个类型训练线性分类器SVM。
作者通过将图片resize为{480,570,688,864,1200}来进行多尺度训练以提高模型表现,还通过fine-tuning预训练模型中的全连接层来获得更好的结果。其全连接层的权重被初始化为σ=0.01的高斯分布,并且将学习率从1e-4调整到1e-5。
最后作者通过分析指出该方法可以使得每个图像的整体测试时间约为0.5秒(包括proposal和识别)。
5 总结
SPP对于处理不同的尺度、尺寸和长宽比是十分灵活的解决方案。它在处理分类和目标检测任务上都表现出了出色的精度和时间优越性。
6 pyTorch实现SPP层
SPP-Net理论理解掌握后,接下来考虑如何实现SPP层。关键在于得到金字塔池化层中对于不同的池化数量中的池化内核尺寸的大小。
该层的计算公式总结为:
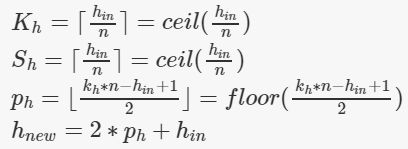
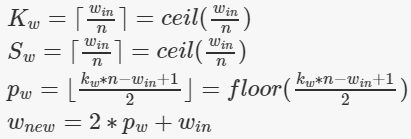
 )
)
注意内核和步长的计算公式都使用的是ceil(),即向上取整,而padding使用的是floor(),即向下取整。
import math
import torch
import torch.nn.functional as F
# 构建SPP层(空间金字塔池化层)
class SPPLayer(torch.nn.Module):
def __init__(self, num_levels, pool_type='max_pool'):
super(SPPLayer, self).__init__()
self.num_levels = num_levels
self.pool_type = pool_type
def forward(self, x):
num, c, h, w = x.size() # num:样本数量 c:通道数 h:高 w:宽
for i in range(self.num_levels):
level = i+1
kernel_size = (math.ceil(h / level), math.ceil(w / level))
stride = (math.ceil(h / level), math.ceil(w / level))
pooling = (math.floor((kernel_size[0]*level-h+1)/2), math.floor((kernel_size[1]*level-w+1)/2))
# 选择池化方式
if self.pool_type == 'max_pool':
tensor = F.max_pool2d(x, kernel_size=kernel_size, stride=stride, padding=pooling).view(num, -1)
if self.pool_type == 'avg_pool':
tensor = F.avg_pool2d(x, kernel_size=kernel_size, stride=stride, padding=pooling).view(num, -1)
# 展开、拼接
if (i == 0):
SPP = tensor.view(num, -1)
else:
SPP = torch.cat((SPP, tensor.view(num, -1)), 1)
return SPP
参考博客1
参考博客2
参考博客3
欢迎关注【OAOA】
![]()