剑指offer--每周总结(一)

另类加法

牛客链接
问题描述：

给定两个int A和B。编写一个函数返回A+B的值，但不得使用+或其他算数运算符。

给定两个int A和B。请返回A＋B的值

class UnusualAdd {
     
public:
int addAB(int A, int B) {
     
while(B!=0)
{
     
int sum=A^B;
int carry=(A&B)<<1;
B=carry;
A=sum;
}
return A;
}
};

解题思路：

• 本题可以通过位运算实现，具体实现如下：
  两个数求和，其实就是 求和后当前位的数据+两个数求和的进位
  例如：
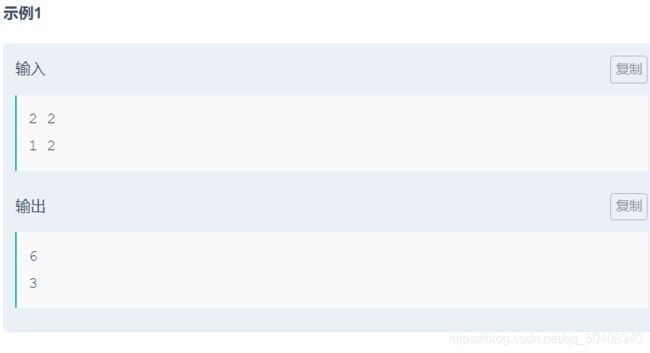
  1 + 2； 00000001 + 00000010
  求和后当前位的数据： 00000011 ； 求和后的进位数据： 没有进位，则 00000000
  两者相加，则得到： 00000011 就是3
  2 + 2； 00000010 + 00000010
  求和后当前位的数据： 00000000， 1和1进位后当前为变成0了
  求和后进位的数据： 00000100， 两个1求和后进位了
  相加后得到： 00000100 就是4
  求和后当前位的数据：简便的计算方法就是两个数进行异或 00000001 ^ 00000010 -> 00000011
  求和后进位的数据：简便的计算方法就是两个数相与后左移一位 (00000010 & 00000010) << 1
  所以这道题使用递归更加容易理解
  代码优化：

class UnusualAdd {
     
public:
int addAB(int A, int B) {
     
if (A == 0) return B;
if (B == 0) return A;
int a = A ^ B;//求和后当前位的数据
int b = (A & B) << 1;//求和后进位的数据
return addAB(a, b);//递归两个数进行相加，任意为0时截止
}
};

求路径总数

牛客链接
问题描述：请计算n*m的棋盘格子（n为横向的格子数，m为竖向的格子数）沿着各自边缘线从左上角走到右下角，总共有多少种走法，要求不能走回头路，即：只能往右和往下走，不能往左和往上走。
输入描述:

每组样例输入两个正整数n和m，用空格隔开。(1≤n,m≤8)

输出描述:

每组样例输出一行结果

#include
using namespace std;
int f(int a, int b) {
     
if (a == 0 || b == 0) {
     
return 1;
}
else {
     
return f(a, b - 1) + f(a - 1, b);
}
}
int main() {
     
int a, b;
while (cin >> a >> b) {
     
cout << f(a , b )<<endl;
}
}

解题思路：

• 题目要求我们从左上角到右下角，而我们从右下角到左上角走，同时要求只能往右和往下走，不能往左和往上走。而我们只能往左和往上走，不能往右边和往下走。
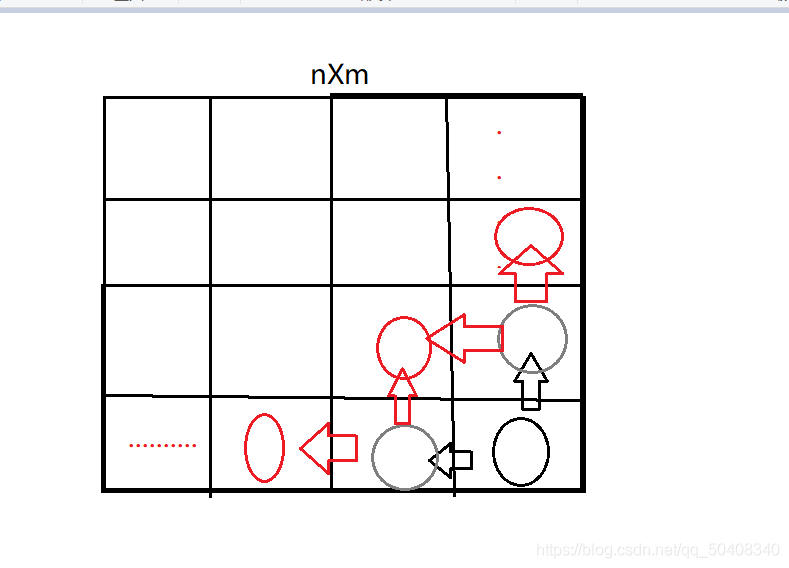
  我们通过可以递归解决问题，
• 当坐标为(n,m）总是有两条路可选(n-1,m)和(n,m-1)，当为0或m为0时坐标为(n,m）可选路就成了一条（0，m）或（n，0） 当n，m都为0时表示已经到达了左上角

1. 对于上面的nm(33)的格子，有两种情况
   a. 如果n或者m为1，则只有一行或者一列，从左上角走到右下角的路径数为n + m
   比如： 1 * 1格子，可以先向下走，再向右走，到达右下角；或者先向右走，
   再向下走，到达右下角，共两条，即 1 + 1 = 2，对于1 * m和 n * m的
   情况同学们自己画一下
   b. 如果n,m都大于1，那么走到[n][m]格子的右下角只有两条路径，
   <1>: 从[n - 1][m]格子的右下角向下走，到达
   <2>: 从[n][m - 1]格子的右下角向右走，到达
   所以走到[n][m]格子的右下角的数量为[n-1][m] + [n][m - 1],可以通过递归实现，情况a为递归的终止条
   件。

2017校招真题：两种排序方法

牛客链接

问题描述：考拉有n个字符串字符串，任意两个字符串长度都是不同的。考拉最近学习到有两种字符串的排序方法：
1.根据字符串的字典序排序。例如：
“car” < “carriage” < “cats” < "doggies < “koala”
2.根据字符串的长度排序。例如：
“car” < “cats” < “koala” < “doggies” < “carriage”
考拉想知道自己的这些字符串排列顺序是否满足这两种排序方法，考拉要忙着吃树叶，所以需要你来帮忙验证。

输入描述:

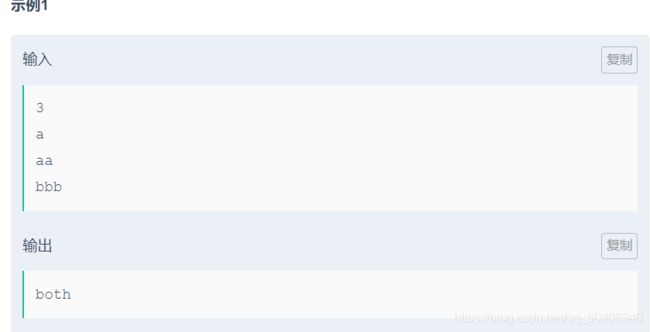
输入第一行为字符串个数n(n ≤ 100) 接下来的n行,每行一个字符串,字符串长度均小于100，均由小写字母组成

输出描述:

如果这些字符串是根据字典序排列而不是根据长度排列输出"lexicographically",

如果根据长度排列而不是字典序排列输出"lengths",

如果两种方式都符合输出"both"，否则输出"none"

解题思路：
本题就是输入一堆字符串，判断字符串是按照字典排序还是长度排序，将接受的字符串都放到vector容器中，利用string的operator>=运算符重载来按ascii比较字符串，利用string的size来比较字符串的长度即可。

#include
#include
#include
using namespace std;
string sort(string *str, int n) {
     
    bool cst=true,lst=true;
    for(int i=1;i<=n;i++){
     
        if(str[i-1]>str[i]){
     
            cst=false;
            break;
        }
    }
     for(int i=1;i<=n;i++){
     
        if(str[i-1].size()>str[i].size()){
     
            lst=false;
            break;
        }
    }
    if(cst&&lst){
     
        return "both";
    }else if(cst==false&&lst){
     
        return "lengths";
        
    }else if(cst&&lst==false){
     
        return "lexicographically";
        
    }
    return "none";
        
}
int main() {
     
    int n, i = 0;
    cin >> n;
    string str[100];
    while (i <= n) {
     
        getline(cin, str[i]);
        i++;
    }
   
    cout << sort(str,n);
}

最小公倍数

牛客链接
问题描述：
正整数A和正整数B 的最小公倍数是指 能被A和B整除的最小的正整数值，设计一个算法，求输入A和B的最小公倍数。
输入描述:
输入两个正整数A和B。

输出描述:
输出A和B的最小公倍数。

解题思路：
思路一：暴力破解：我们从最大数依次遍历每次加一直到找到第一个能被两个数同时整除。

#include
using namespace std;
int main(){
     
    int a,b,c=0;
    cin>>a>>b;
    c=a>b?a:b;
    for(int i=c;c<=a*b;i++){
     
        if(i%a==0&&i%b==0){
     
            cout<<i<<endl;
            break;
        }
    }
}

思路二
更优解法：
最小公倍数=两数乘积/最大公约数。
最大公约数：辗转相除法；

a=9,b=6
a%b == 3
a=b,b=3
a%b == 0;
a=b，b=0
结束 最大公约数为a

#include
using namespace std;
void stt(int a,int b){
     
    int c=0,a1=a,b1=b;
    while(b!=0){
     //求最大公约数
       c= a%b;
        a=b;
        b=c;
    }
    cout<<a1*b1/a<<endl;
}
int main(){
     
    int a,b;
    cin>>a>>b;
    stt(a,b);
}

Fibonacci数列

牛客链接
问题描述：

• Fibonacci数列是这样定义的：
  F[0] = 0
  F[1] = 1
  for each i ≥ 2: F[i] = F[i-1] + F[i-2]
  因此，Fibonacci数列就形如：0, 1, 1, 2, 3, 5, 8, 13, …，在Fibonacci数列中的数我们称为Fibonacci数。给你一个N，你想让其变为一个Fibonacci数，每一步你可以把当前数字X变为X-1或者X+1，现在给你一个数N求最少需要多少步可以变为Fibonacci数。
  输入描述：
  输入为一个正整数N(1 ≤ N ≤ 1,000,000)
  输出描述:
  输出一个最小的步数变为Fibonacci数"

解题思路：

• 本题可以通过先找到距离N最近的两个Fibonacci数，这两个数分别取自距离N的最近的左边一个数L和右边一个
  数R，然后通过min(N - L, R - N)找到最小步数。
• 找到最靠近它比他小的值，当找到第一个比它大的值就break

f1=0,f1=1
递归体
f=f1+f2
f1=f2
f2=f

#include
using namespace std;
int main(){
     
    int f=0,f1=0,f2=1;
    int left=0,right=0;
    int N;
    cin>>N;
    while(1){
     
        f=f1+f2;
     
        f1=f2;
           f2=f;
        if(N>f){
     
            left=f;//找到最靠近它比他小的值
        }else{
     
            right=f;//当找到第一个比她大的值就break
            break;
        }
    }
    int num=(N-left)<(right-N)?(N-left):(right-N);
    cout<<num<<endl;
    return 0;
}

合法括号序列排序

牛客链接

题目描述
给定一个字符串A和其长度n，请返回一个bool值代表它是否为一个合法的括号串（只能由括号组成）。

测试样例：

“(()())”,6
返回：true

测试样例：

“()a()()”,7

返回：false

测试样例：

“()(()()”,7
返回：false

解题思路：
我们只要排除不匹配的情况就行：

1. 当前字符不是括号字符
2. 括号匹配不完整
   多出来左半括号
   多出来右半括号
   思想：遍历字符串，遇到左半边就放入队列中，遇到右半边，则查看有没有匹配的括号。若没有队列为空，匹配不完整，多出了右半边。
   有，则出队列与其匹配为完整括号遍历完毕后如果队列不为空，则表示多出了左半边。

class Parenthesis {
     
public:
  bool chkParenthesis(string A, int n) {
     
    // write code here
   queue<char> v;
    string::iterator it = A.begin();
    while (it != A.end()) {
     
        
       switch(*it){
     
           case '(':
               v.push(*it);
               break;
           case ')':
               if(v.empty()){
     
                   return false;//  多出来右半括号
               }
               v.pop();
               break;
           default:
               return false;//非括号
       }
        it++;
    }
    
    return v.empty();//多出来左半括号
}

};

不要二

牛客链接
题目描述
二货小易有一个W*H的网格盒子，网格的行编号为0_{H-1，网格的列编号为0}W-1。每个格子至多可以放一块蛋糕，任意两块蛋糕的欧几里得距离不能等于2。
对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为:
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根
小易想知道最多可以放多少块蛋糕在网格盒子里。
输入描述:

每组数组包含网格长宽W,H，用空格分割.(1 ≤ W、H ≤ 1000)

输出描述:

输出一个最多可以放的蛋糕数

解题思路：
本题的重点是要读懂题意，并且需要多读两遍，才能读懂，本题本质就是在二维数组中每个坐标去放蛋糕，一个坐标位置放了蛋糕，跟他欧几里得距离为2的位置不能放蛋糕，这个就是关键点。对于两个格子坐标(x1,y1),
(x2,y2)的欧几里得距离为: ( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根 。
也就是说：如果(x1,y1)放了蛋糕，则满足 ( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4的(x2,y2)不能放蛋
糕。
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4看起来是一个无解的表达式。
但是可以进行加法表达式分解：
1+3=4
3+1=4
2+2=4
0+4=4
4+0=4
仔细分析前三个表达式是不可能的，因为(x1-x2) * (x1-x2)表达式结果不能等于2或3。
也就是说( (x1-x2) * (x1-x2) 和(y1-y2) * (y1-y2) )两个表达式一个等于0，一个等于4.
可以看出：假设放蛋糕的位置是(x1,y1)，则不能放蛋糕的位置(x2,y2)，满足x1== x2,y1-y2 == 2或者x1-x2 == 2,y1 == y2.

#include
using namespace std;
int main(){
     
	int w,h;
	cin>>w>>h;
	int count = 0;
	for(int i = 0;i<h;i++){
     
		int j =0;
		if(i/2%2 !=0){
     
			j=2;
	}
	for(;j<w;j+=4){
     
		if( j+1<w){
     
			count +=2;
		}else{
     
			count+=1;
			}
		}
	}
cout<<count;
}

把字符串转成整数

牛客链接
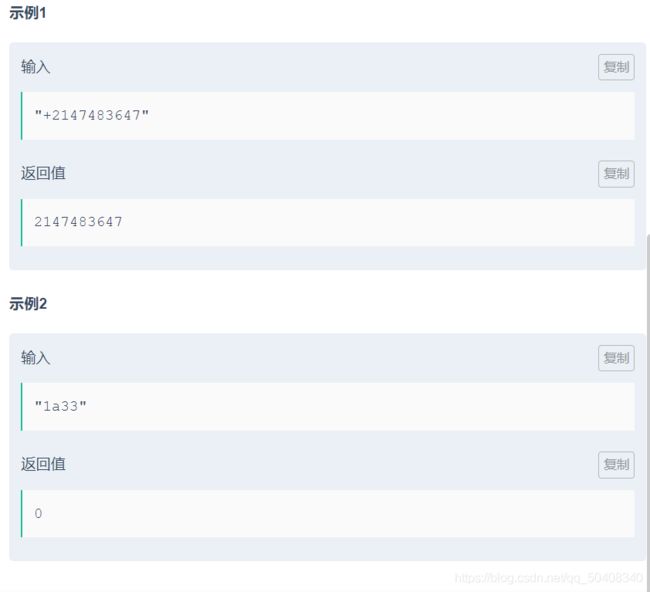
输入描述:
输入一个字符串,包括数字字母符号,可以为空
返回值描述:
如果是合法的数值表达则返回该数字，否则返回0

解题思路：
解题思路非常简单，就是上次计算的结果10，相当于10进制进位，然后加当前位的值。
例如：“123”转换的结果是
sum=0
sum10+1->1
sum10+2->12
sum10+3->123

本题的关键是要处理几个关键边界条件：

1. 空字符串
2. 正负号处理
3. 数字串中存在非法字符

class Solution {
     
public:
    int StrToInt(string str) {
     
        int sum=0,num=0;
        int c=1,b=0;
        
        if(str[0]=='+'){
     
            c=1;
            b=1;
        }
        if(str[0]=='-'){
     
            c=-1;
            b=1;
        }
    string::iterator it=str.begin()+b;
     while(it!=str.end()){
     
        if (*it >'9' || *it < '0') {
     
            return 0;
        }
         num=*it-'0';
         sum=sum*10+num;
         it++;
     }
        if(c==-1){
     
           return -sum;  
        }
        return sum;
    }
};