实现一元线性回归
课程回顾
逻辑回归
在上一节课中我们介绍了逻辑回归,逻辑回归是在线性模型的基础上,再增加一个sigmoid的函数来实现的。
y = σ ( w x + b ) = 1 1 + e − ( w x + b ) y=\sigma(wx+b)=\frac{1}{1+e^{-(wx+b)}} y=σ(wx+b)=1+e−(wx+b)1
输入样本特征,
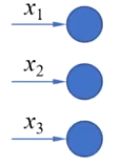
经过线性组合之后得到的是一个连续值。
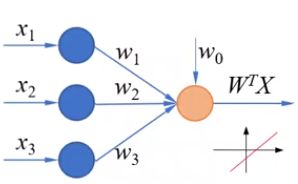
经过sigmoid函数把它转化为一个0~1之间的概率。
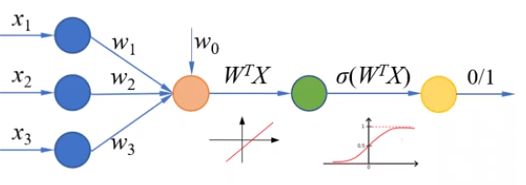
通过设置合理的阈值就可以实现二分类问题。
分类器的目标是希望正确分类的比例尽可能高。在模型训练好之后,可以使用准确率来评价分类器的性能。它是分类器能够正确分类的样本数与样本总数之比。
准 确 率 = 正 确 分 类 的 样 本 数 总 样 本 数 准确率=\frac{正确分类的样本数}{总样本数} 准确率=总样本数正确分类的样本数
在模型训练的过程中,为了更加细致准确的表示模型的误差需要使用损失函数。
交叉熵损失函数用来刻画概率之间的误差,它具备作为损失函数的基本性质。
- 每一项误差的值都是非负的
- 函数值和误差的变化趋势一致
当样本的标签和分类器的输出越接近时,函数的值就越接近于0 - 逻辑回归的交叉熵损失函数是一个凸函数
可以使用梯度下降法得到全局最小值 - 并且它对模型参数求偏导数时,不用计算 σ ′ ( ) \sigma'() σ′()函数的导数
因为交叉熵损失函数具备以上这些优良的特性,在分类问题中最好使用它作为损失函数,从而避免平方损失函数训练过程太慢或者可能陷入局部最小值的问题。
在这节课中我们就来使用tensorflow编程,实现逻辑回归,在实现逻辑回归时,需要计算sigmoid函数、准确率和交叉熵损失函数。首先我们来看一下如何使用tensorflow实现这些运算。
实现sigmoid()函数
sigmoid()函数
这是sigmoid函数的表达式。
y = σ ( w x + b ) = 1 1 + e − ( w x + b ) y=\sigma(wx+b)=\frac{1}{1+e^{-(wx+b)}} y=σ(wx+b)=1+e−(wx+b)1
import tensorflow as tf
import numpy as np
# x是一个长度为4的一维数组
x = np.array([1, 2, 3, 4])
# W和B都是数字
w = tf.Variable(1.)
b = tf.Variable(1.)
y = 1/(1+tf.exp(-(w*x+b)))
# 结果也是一个长度为4的一维张量
# tensorflow中使用exp函数来实现e的x次方的运算。
tf.exp()
要注意,这个函数的参数要求是浮点数,否则会报错。
这是交叉熵损失函数的表达式。
L o s s = − ∑ i = 1 n [ y i l n y i ^ + ( 1 − y i ) l n ( 1 − y i ^ ) ] Loss=-\sum_{i=1}^n[y_iln{\hat{y_i}}+(1-y_i)ln(1-\hat{y_i})] Loss=−∑i=1n[yilnyi^+(1−yi)ln(1−yi^)]
# y是样本标签
y = np.array([0, 0, 1, 1])
# pred是预测概率
pred = np.array([0.1, 0.2, 0.8, 0.49])
# `1-y`和`1-pred`做广播运算结果也是一维数组
1-y
# array([1, 1, 0, 0])
1-pred
# array([0.9 , 0.8 , 0.2 , 0.51])
-tf.reduce_sum(y*tf.math.log(pred)+(1-y)*tf.math.log(1-pred))
# 假设,y是样本标签,pred是预测概率。
在tensorflow中使用,math.log()函数实现以e为底的对数运算。
tf.math.log()
y和pred都是一维数组,1-y和1-pred做广播运算结果也是一维数组。
y*tf.math.log(pred)+(1-y)*tf.math.log(1-pred)这是每一个样本的交叉熵损失,对他们求和tf.reduce_sum(y*tf.math.log(pred)+(1-y)*tf.math.log(1-pred))就可以得到所有样本的交叉熵损失,要记住前面还有一个负号。
使用tf.reduce_mean()函数可以得到平均交叉熵损失-tf.reduce_mean(y*tf.math.log(pred)+(1-y)*tf.math.log(1-pred))。
准确值
准确率是正确分类的样本数除以样本总数。
通过sigmoid()函数得到的预测值是一个概率,首先要把它转换为类别0或1。
# 准确率
# y是样本标签
y = np.array([0, 0, 1, 1])
# pred是预测概率
pred = np.array([0.1, 0.2, 0.8, 0.49])
"""如果将阈值设置为0.5,那么可以使用四舍五入函数round()的把它转化为0或1"""
tf.round(pred)
# 如果将阈值设置为0.5,那么可以使用四舍五入函数round()的把它转化为0或1,然后使用equal()函数逐元素的去比较预测值和标签值,得到的结果是一个和y、pred形状相同的一维张量。
可以看到其中前三对元素是相同的,最后一对元素不相同。
下面使用cast()函数把这个结果转化为整数,然后对它的所有元素求平均值,就可以得到正确样本在所有样本中的比例。
要注意的是使用round()函数时,如果参数恰好是0.5,那么返回的结果是0,当参数的值大于0.50,结果才是1。
where(condition, a, b)
在这个例子中,我们假设阈值为0.5,那么如果阈值不是0.5而是其他的值,应该怎样处理呢?
在tensorflow中提供了where()函数,它根据条件condition返回a或者B的值。
参数condition是一个布尔型的张量或者数组,如果condition中的某个元素为真,那么对应位置就返回a,否则返回b。
例如当pred中的元素小于0.5时,相应的元素返回0,否则返回1。
pred = np.array([0.1, 0.2, 0.8, 0.49])
tf.where(pred < 0.5, 0, 1)
这是运行的结果。
# 其中pred小于0.5会用pred数组中的每一个元素和0.5比较,返回一个布尔型的数组。
pred < 0.5
# array([ True, True, False, True])
也可以把阈值设置为0.4,这是得到的结果。
tf.where(pred < 0.4, 0, 1)
# 参数a和b还可以是数组或者张亮。这时,a和b必须有相同的形状,并且他们的第1维必须和condition形状一致。
例如,首先创建数组a和b。
pred = np.array([0.1, 0.2, 0.8, 0.49])
a = np.array([1, 2, 3, 4])
b = np.array([10, 20, 30, 40])
当pred中的元素小于0.5时就返回a中对应位置的元素,否则返回B中对应位置的元素,这是运行的结果。
tf.where(pred < 0.5, a, b)
<tf.Tensor: id=109, shape=(4,), dtype=int32, numpy=array([ 1, 2, 30, 4])>
可以看到数组pred 中第1、2、4个元素都小于0.5,因此取数组a中的元素。而第3个元素大于0.5,所以这个位置取b中的元素。如果需要返回不同的值,可以采用这种方法。
参数a和b也可以省略,这时的返回值就是数组pred中大于等于0.5的元素的索引,这个返回值以一个二维张量的形式给出,这在我们需要获取满足某种条件的掩码是非常有用。
tf.where(pred >= 0.5)
# 在计算分类准确率时,使用where()函数可以更加灵活的设置阈值,将预测概率转化为类别,这是得到的分类准确率。
y = np.array([0, 0, 1, 1])
pred = np.array([0.1, 0.2, 0.8, 0.49])
tf.reduce_mean(tf.cast(tf.equal(tf.where(pred < 0.5, 0, 1), y), tf.float32))
# 实现一元逻辑回归
下面我们就来使用一元逻辑回归实现对商品房的分类,这是商品房的面积,这是类型。0代表普通住宅,1代表高档住宅。
房屋销售记录
| 序号 | 面积(平方米) | 类型 | 序号 | 面积(平方米) | 类型 |
|---|---|---|---|---|---|
| 1 | 137.97 | 1 | 9 | 106.69 | 0 |
| 2 | 104.50 | 1 | 10 | 140.05 | 1 |
| 3 | 100.00 | 0 | 11 | 53.75 | 0 |
| 4 | 126.32 | 1 | 12 | 46.91 | 0 |
| 5 | 79.20 | 0 | 13 | 68.00 | 0 |
| 6 | 99.00 | 1 | 14 | 63.02 | 0 |
| 7 | 124.00 | 1 | 15 | 81.26 | 0 |
| 8 | 114.00 | 0 | 16 | 86.21 | 0 |
在前面的例子中我们曾经讲过,根据房价是否大于100万来分类,其实这只是为了方便大家理解,可以看到在这个分类问题的数据集中是没有房价这个标签的,而是直接使用面积和所属的类别来训练模型。
在模型的训练过程中产生的线性模型, w x + b wx+b wx+b的值,我们可以把它理解为类似于房价的一个指标,它是一个中间结果,我们并不需要把它读取出来。
这个例子中的数据和前面的例子稍微有点不同,修改了这两个数据(序号4和10),这是为了避免在做散点图时和其他相邻的点重合。
第1步加载数据
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.array([137.97, 104.50, 100.00, 126.32, 79.20, 99.00, 124.00, 114.00,
106.69, 140.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])
y = np.array([1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0])
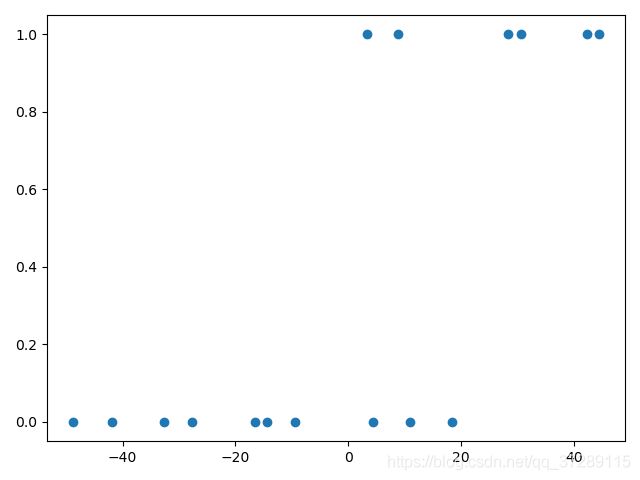
plt.scatter(x, y)
plt.show()

这是训练数据对应的散点图,横坐标是面积,纵坐标是类别,可以看到类别只有0和1两种取值,这里面积都是大于40的正数,因为sigmoid()函数是以零点为中心的。
第2步数据处理
因此在数据处理阶段,我们对这些点进行中心化。每个样本点都减去他们的平均值,这样整个数据集的均值就等于0。
x_train = x - np.mean(x)
y_train = y
plt.scatter(x_train, y_train)
plt.show()
第3步设置超参数和显示间隔
learn_rate = 0.005
iter = 5
display_step = 1
第4步设置模型变量的初始值
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())
第5步训练模型
"""cross_train用来存放训练集的交叉熵损失"""
cross_train = []
"""acc_train用来存放训练集的分类准确率"""
acc_train = []
for i in range(0, iter + 1):
with tf.GradientTape() as tape:
"""这是计算sigmoid()函数"""
pred_train = 1/(1 + tf.exp(-(w*x_train+b)))
"""这是交叉熵损失函数"""
Loss_train = -tf.reduce_mean(y_train*tf.math.log(pred_train)+(1-y_train)*tf.math.log(1-pred_train))
"""这是计算准确率,因为不需要对它进行求导运算,因此也可以把这条语句写在with语句的外面"""
Accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(pred_train < 0.5, 0, 1), y_train), tf.float32))
# Accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(pred_train < 0.5, 0, 1), y_train), tf.float32))
"""记录每一次迭代的损失和准确率"""
cross_train.append(Loss_train)
acc_train.append(Accuracy_train)
"""获得损失函数对w和b的偏导数"""
dL_dw, dL_db = tape.gradient(Loss_train, [w, b])
"""更新模型参数"""
w.assign_sub(learn_rate * dL_dw)
b.assign_sub(learn_rate * dL_db)
"""输出训练过程和结果"""
if i % display_step == 0:
print("i: %i, Train Loss: %f, Accuracy: %f" % (i, Loss_train, Accuracy_train))
这是运行的结果。
i: 0, Train Loss: 0.852807, Accuracy: 0.625000
i: 1, Train Loss: 0.400259, Accuracy: 0.875000
i: 2, Train Loss: 0.341504, Accuracy: 0.812500
i: 3, Train Loss: 0.322571, Accuracy: 0.812500
i: 4, Train Loss: 0.313972, Accuracy: 0.812500
i: 5, Train Loss: 0.309411, Accuracy: 0.812500
可以看到损失一直在下降。
i: 0, Train Loss: 0.852807, Accuracy: 0.625000 10/16
i: 1, Train Loss: 0.400259, Accuracy: 0.875000 14/16
i: 2, Train Loss: 0.341504, Accuracy: 0.812500 13/16
i: 3, Train Loss: 0.322571, Accuracy: 0.812500
i: 4, Train Loss: 0.313972, Accuracy: 0.812500
i: 5, Train Loss: 0.309411, Accuracy: 0.812500
这是准确率,第1次对10个样本分类正确,第2次对14个样本分类正确,然后稳定在13个样本,
为了更好的观察训练的过程,我们可以绘制出每轮迭代时sigmoid()函数的曲线。在设置模型初始值之后,给出一组连续的x坐标,并使用w和b的初始值计算sigmoid()函数的值作为y坐标。
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())
x_ = range(-80, 80)
y_ = 1/(1+tf.exp(-(w*x_+b)))
plt.plot(x_, y_)
plt.show()
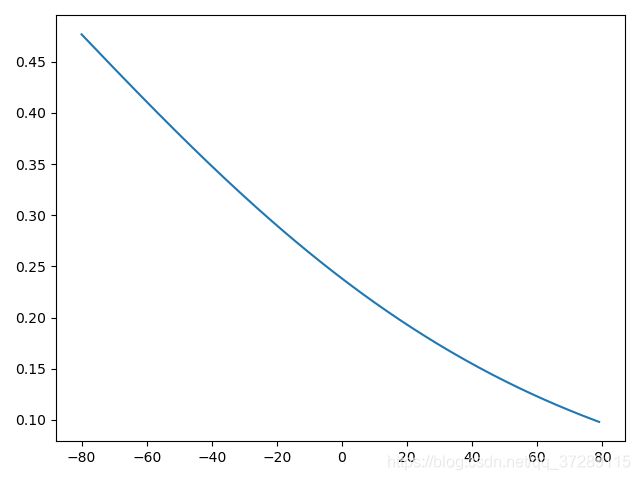
绘制曲线图就得到了使用w和b的初始值时的sigmoid()函数曲线。这个曲线看起来和S型曲线相差很大,是因为这个随机的w和b正好得到了一个中间变化部分范围很大的曲线。
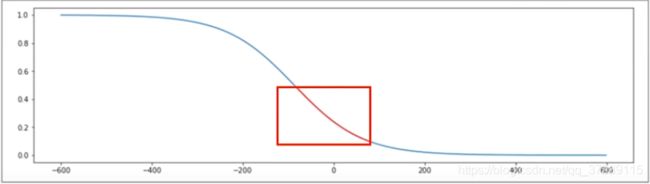
在-80~正80的这个区间,只是其中的一小部分。
第6步可视化输出
现在在训练模型的过程中增加sigmoid()曲线的可视化输出。在迭代之前输出训练数据的散点图和使用初始模型参数时的sigmoid()曲线。为了便于区分,使用红色线条宽度为3。
# 第1步加载数据
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.array([137.97, 104.50, 100.00, 126.32, 79.20, 99.00, 124.00, 114.00,
106.69, 140.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])
y = np.array([1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0])
# plt.scatter(x, y)
# plt.show()
# 第2步数据处理
x_train = x - np.mean(x)
y_train = y
plt.scatter(x_train, y_train)
# plt.show()
# 第3步设置超参数和显示间隔
learn_rate = 0.005
iter = 5
display_step = 1
# 第4步设置模型变量的初始值
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())
x_ = range(-80, 80)
y_ = 1/(1+tf.exp(-(w*x_+b)))
plt.plot(x_, y_)
# 可视化输出
plt.scatter(x_train, y_train)
plt.plot(x_, y_, color="red", linewidth=3)
# 第5步训练模型
cross_train = []
acc_train = []
for i in range(0, iter + 1):
with tf.GradientTape() as tape:
pred_train = 1/(1 + tf.exp(-(w*x_train+b)))
Loss_train = -tf.reduce_mean(y_train*tf.math.log(pred_train)+(1-y_train)*tf.math.log(1-pred_train))
Accuracy_train = tf.reduce_mean(tf.cast(tf.equal(tf.where(pred_train < 0.5, 0, 1), y_train), tf.float32))
cross_train.append(Loss_train)
acc_train.append(Accuracy_train)
dL_dw, dL_db = tape.gradient(Loss_train, [w, b])
w.assign_sub(learn_rate * dL_dw)
b.assign_sub(learn_rate * dL_db)
if i % display_step == 0:
print("i: %i, Train Loss: %f, Accuracy: %f" % (i, Loss_train, Accuracy_train))
y_ = 1/(1+tf.exp(-(w*x_+b)))
plt.plot(x_, y_)
plt.show()
在每次输出时都绘制使用当前全值时的sigmoid()曲线,这是运行的结果。

这是使用初始模型参数时的sigmoid()函数曲线,虽然看起来很离谱,但是恰好属于普通住宅的这10个样本的概率都在0.5以下所以分类正确率是10/16,这只能说是运气蒙对了。
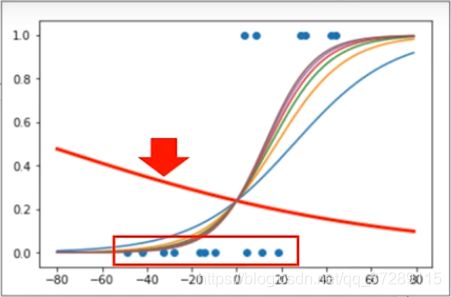
这是第1次迭代后的结果。
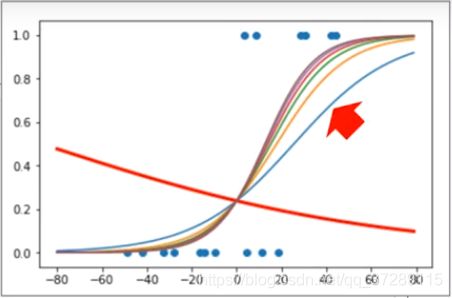
这是最后一次迭代后的结果。
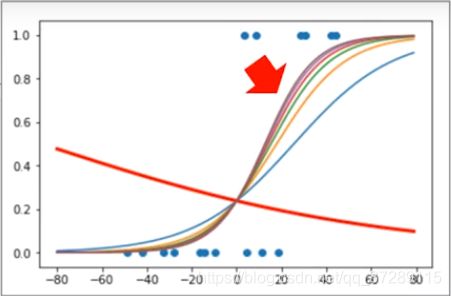
可以看到随着训练次数的增加,输出概率越来越能够反映出样本的真实分类了。
因为这两类样本不是恰好在横坐标为零时分开的有一定的交集,所以这个区域中的点可能会出现分类错误,导致准确率无法达到100%。
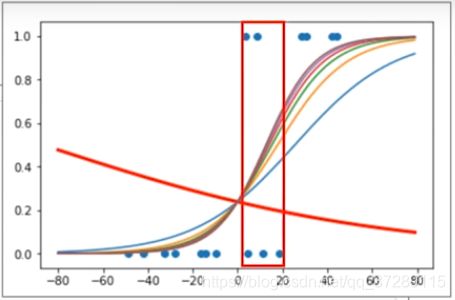
这个第1次训练的结果分类的准确率虽然更高,但是从整体来看还是经过更多次迭代之后,概率的预测更加合理。
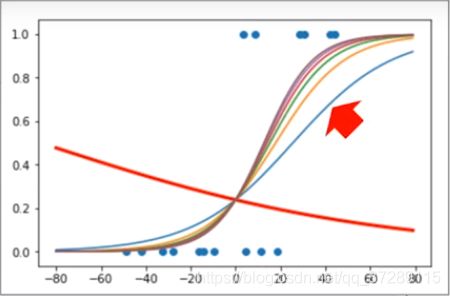
第7步使用模型,进行分类
下面就可以使用这个模型对新的商品房进行分类了。
"""这是商品房面积"""
x_test = [128.15, 45.00, 141.43, 106.27, 99.00, 53.84, 85.36, 70.00, 162.00, 114.60]
"""根据面积计算概率,np.mean(x)这里使用训练数据的平均值,对新的数据进行中心化处理"""
pred_test = 1/(1+tf.exp(-(w*(x_test-np.mean(x))+b)))
"""根据概率进行分类"""
y_test = tf.where(pred_test<0.5, 0, 1)
for i in range(len(x_test)):
print(x_test[i], "\t", pred_test[i].numpy(), "\t", y_test[i].numpy(), "\t")
这是预测的概率和分类
128.15 0.8610252 1
45.0 0.0029561974 0
141.43 0.9545566 1
106.27 0.45318928 0
99.0 0.2981362 0
53.84 0.00663888 0
85.36 0.108105935 0
70.0 0.028681064 0
162.0 0.9928677 1
114.6 0.6406205 1
要注意的是这里虽然使用x_test来表示这些数据,但是他们并不是测试集。
测试集是有标签的数据,例如我们使用的波士顿房价数据集中的测试集,就是有标签的。在训练的过程中通过模型在测试集上的表现来评价模型的性能,在机器学习中要求测试集和训练集是独立同分布的,也就是说它们有着相同的均值和方差,这样的测试才有意义。
而这里的这个x_test实际上是模型训练好之后,在真实场景下的应用情况,是没有标签的。真实场景中的数据可能是各种各样的,而且通常来说每次应用可能只是给出一个数据或者一部分数据,所以这里采用训练集中的均值来中心化数据。
第8步把分类的结果可视化输出
下面把分类的结果可视化输出,首先根据分类结果绘制散点图。
plt.scatter(x_test, y_test)
x_ = np.array(range(-80, 80))
y_ = 1/(1+tf.exp(-(w*x_+b)))
"""因为散点图的X坐标使用的是真实的面积,没有平移,所以在这里加上训练级的均值np.mean(x)平移曲线"""
plt.plot(x_+np.mean(x), y_)
plt.show()

可以看到这4套商品房被划分为高档住宅。
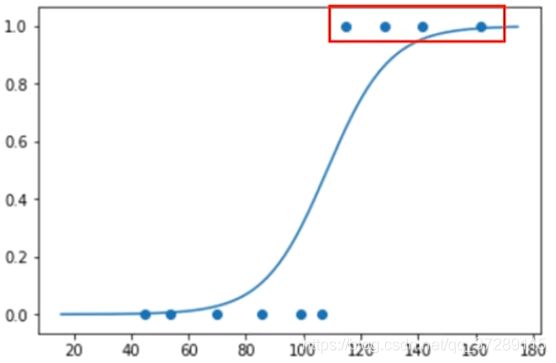
这些被划分为普通住宅。
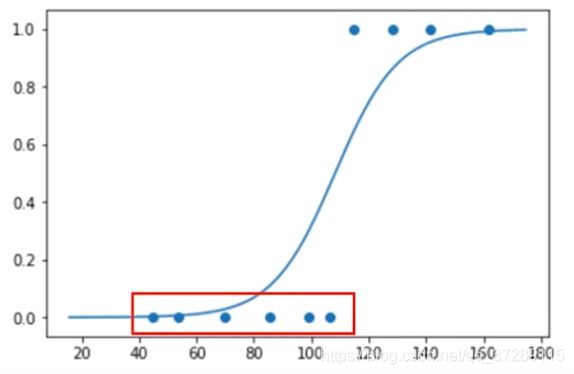
通过散点图可以更加直观的看到商品房类型和面积之间的关系,然后绘制概率曲线,因为散点图的X坐标使用的是真实的面积,没有平移,所以在这里加上训练级的均值平移曲线。