详解线性回归算法的纯Python实现

↑↑↑关注后"星标"简说Python人人都可以简单入门Python、爬虫、数据分析 简说Python推荐 
来源｜天池大数据科研平台作者｜黄佳

零基础学机器学习——一文详解线性回归算法的纯Python实现

❝

本文作者：黄佳，新加坡埃森哲公司高级顾问，人工智能专家，机器学习和云计算高级工程师，参与过公共事业、医疗、金融等多领域大型项目。著有《零基础学机器学习》，《SAP程序设计》，《SAP高级应用开发》，《SAP业务数据传输指南》。

❞

写在前面

大家好，说到牛年春晚，最吸引眼球的并不是哪一位明星，而是这个超级酷炫的“AI拓荒牛”。

看起来如此高大上，如此梦幻的机器“牛”，它们的“智能”是怎么实现的，其实背后的核心算法离不开机器学习。

说到机器学习，大家可能会马上联想到艰深的算法，复杂的公式和高等数学。的确，算法和高等数学确实是机器学习时的基础知识储备。不过，我们也可以用比较浅显易懂的方法介绍一些机器学习相关的入门内容和基础算法。你会惊奇的发现入门机器学习并没有想象中那么高的门槛。

那么何为机器学习？

机器学习的关键内涵之一在于「利用计算机的运算能力从大量的数据中发现一个“函数”或“模型”，并通过它来模拟现实世界事物间的关系，从而实现预测或判断的功能。」 这个过程的关键是建立一个正确的模型，因此这个建模的过程就是机器的“学习”。

比如，一颗钻石的大小（自变量x1）、重量（自变量x2）、颜色（自变量x3）、密度（自变量x4）和它的价格（因变量y）的关系，就体现出了明显的相关性，如下图所示。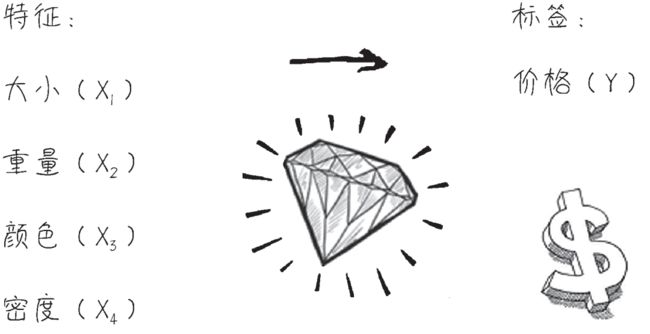这些自变量（x1, x2, x3, …, xn），在机器学习领域叫作特征（feature），因变量y ，在机器学习领域叫作标签（label）。「机器学习，就是在已知数据集的基础上，通过反复的计算，选择最贴切的函数（function）去描述数据集中特征和标签之间的关系」。

如果机器通过所谓的训练（training）找到了一个函数，对于已有的1000组钻石数据，它都能够根据钻石的各种特征，大致推断出其价格。那么，再给另一批同类钻石的大小、重量、颜色、密度等数据，就很有希望用同样的函数（模型）推断出这另一批钻石的价格。此时，已有的1000组有价格的钻石数据，就叫作「训练数据集」。另一批钻石数据，就叫作「测试数据集」。

通过机器学习模型不仅可以推测钻石价格，还可以实现影片票房预测、人脸识别、根据当前场景控制游戏角色的动作等诸多功能。

好了，那么关于机器学习最基本的知识我们就介绍到这里。今天我们将从无到有，来通过Python语言搭建一个非常简单的线性回归机器学习模型，并利用这个模型来预测一个零售网店的日销售额。

这次实战的数据集和源代码都可以在阿里云天池中下载：

使用浏览器访问下方地址，在《零基础学机器学习》读书会中可以点击实践代码，即可获取全部代码和数据：

https://tianchi.aliyun.com/specials/promotion/activity/bookclub

机器学习项目实战框架

开始构建机器学习模型之前，我们要先简单介绍一下机器学习项目的实战框架，大致分为以下5个环节。

1. 问题定义。

2. 数据的收集和预处理。

3. 模型（算法）的选择。

4. 选择机器学习模型。

5. 超参数调试和性能优化。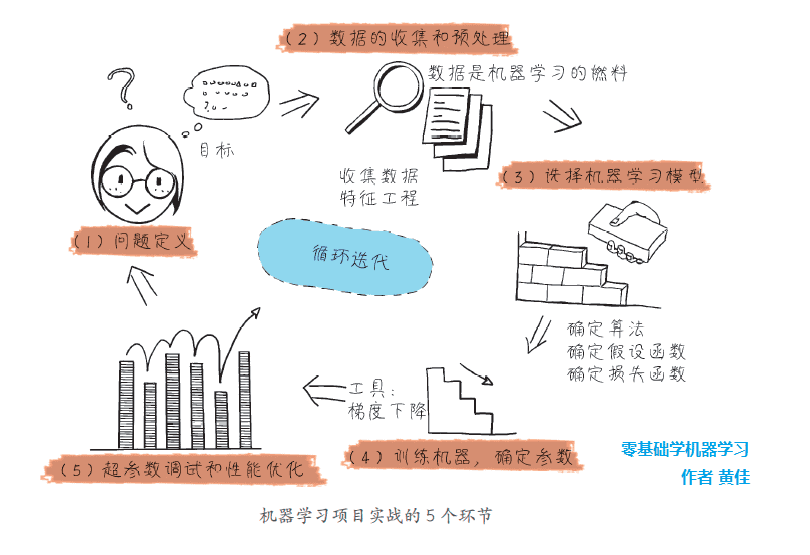这5个环节，每一步的处理是否得当，都直接影响机器学习项目的成败。而且，这些步骤还需要在项目实战中以迭代的方式反复进行，以实现最优的效果。

一个实际问题的定义

来看一下我们今天要解决的问题是什么？

小冰和朋友合伙开一个网店，这个店的基本情况是这样的：正式运营一年多，流量、 订单数和销售额都显著增长。经过一段时间的观察，小冰发现网店商品的销量和广告推广的力度息息相关。她在微信公众号推广，也通过微博推广，还在一些其他网站上面投放广告。当然，投入推广的资金越多，则商品总销售额越多。小冰问她的机器学习导师咖哥：“能不能通过机器学习算法，根据过去记录下来的广告投放金额和商品销售额，来预测在未来的某个节点，一个特定的广告投放金额对应能实现的商品销售额？”

那么基于这个问题来说呢，数据集的特征就是在各个平台上投放的广告金额（平台可以不止一个），而标签呢，也就是我们要预测的：商品销售额。

数据收集和预处理

小冰已经把过去每周的广告投放金额和销售额数据整理成一个 Excel 表格，并保存为advertising.csv 文件，便于被Python读取。基本上每周的各种广告投放金额和商品销售额都记录在案。

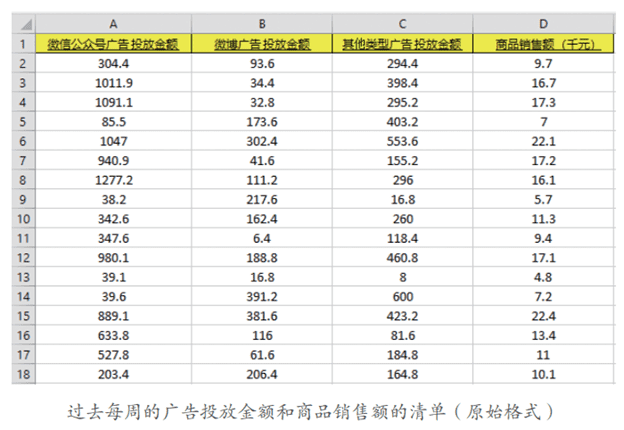
这个数据记录是实现本课的机器学习项目的基础。没有准确的历史数据，我们是什么都做不了的。

显示数据

用Python代码来显示一下读入的数据：

import numpy as np # 导入NumPy 库
import pandas as pd # 导入Pandas 库
# 读入数据并显示前面几行的内容, 确保已经成功地读入数据
# 示例代码是Kaggle 的数据集读入文件, 如果在本机中则需要指定具体本地路径
# 如，当数据集和代码文件位于相同本地目录，路径名应为'./advertising.csv'，或直接为'advertising.
# csv' 亦可
df_ads = pd.read_csv('../input/advertising-simple-dataset/advertising.csv')
df_ads.head()

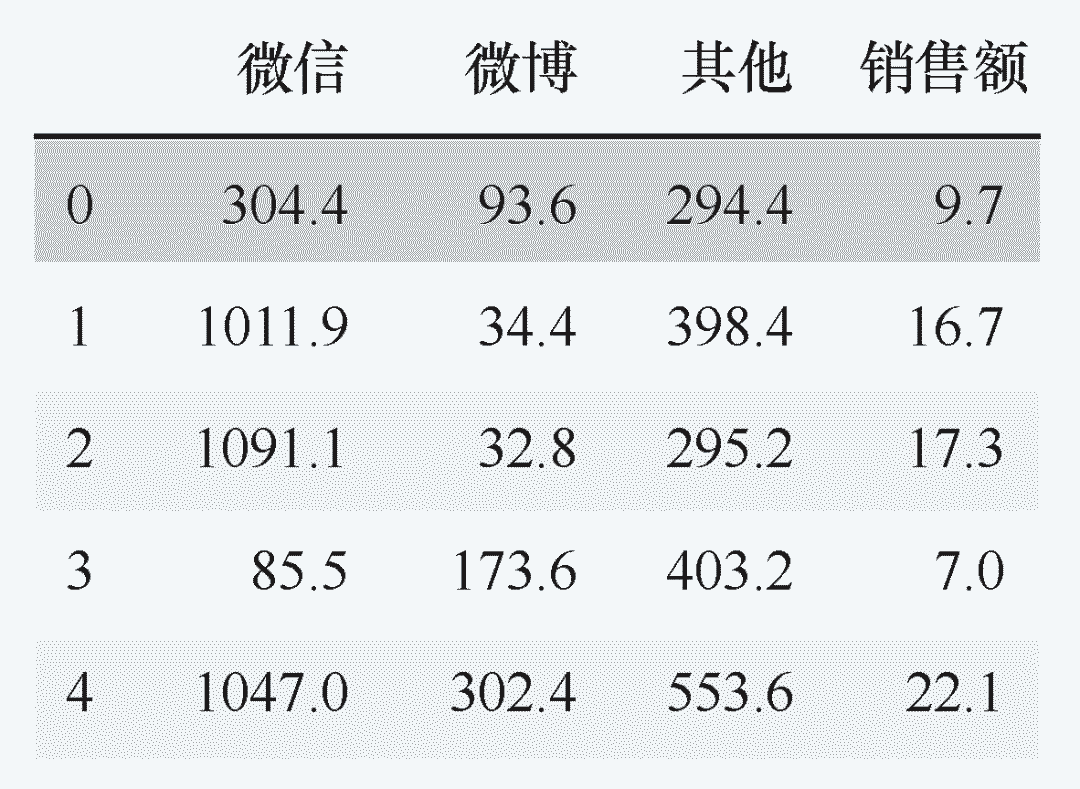
相关分析

我们在这里会做一些相关分析，看看所选择的特征和标签之间的关系。相关性系数是一个-1 ～ 1 之间的值，正值表示正相关，负值表示负相关。数值越大，相关性越强。

• 如果a和b的相关性系数是1，则a和b总是相等的。如果a 和b 的相关性系数是0.9，则b 会显著地随着a 的变化而变化，而且变化的趋势保持一致。

• 如果a 和b 的相关性系数是0.3，则说明两者之间并没有什么明显的联系。

# 导入数据可视化所需要的库
import matplotlib.pyplot as plt #Matplotlib 为Python 画图工具库
import seaborn as sns #Seaborn 为统计学数据可视化工具库
# 对所有的标签和特征两两显示其相关性的热力图
sns.heatmap(df_ads.corr(), cmap="YlGnBu", annot = True)
plt.show() #plt 代表英文plot, 就是画图的意思

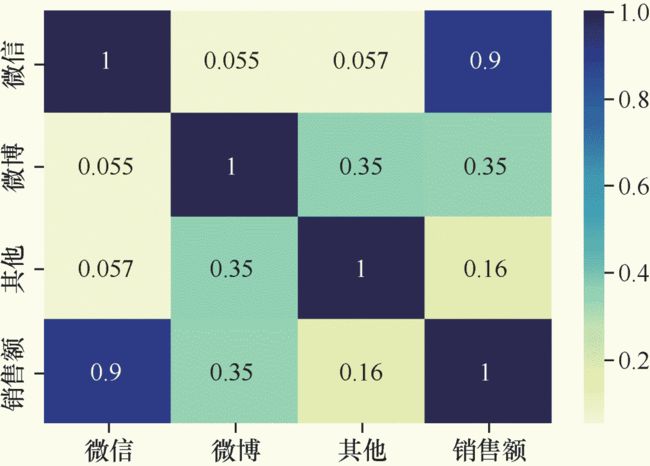
散点图

下面，通过散点图两两一组显示商品销售额和各种广告投放金额之间的对应关系，来将重点聚焦。散点图是回归分析中，数据点在直角坐标系平面上的分布图，它是相当有效的数据可视化工具。

# 显示销售额和各种广告投放金额的散点图
sns.pairplot(df_ads,
x_vars=['wechat', 'weibo', 'others'],
y_vars='sales',
height=4, aspect=1, kind='scatter')
plt.show()

代码运行之后输出的散点图清晰地展示出了销售额随各种广告投放金额而变化的大致趋势， 根据这个信息，就可以选择合适的函数对数据点进行拟合。

其实在这里，我们就基本上可以看出微信广告和销售额之间呈现的是一种线性关系，可以选择线性回归进行拟合，不过这是后话。

通过观察相关性和散点图，发现在本案例的3个特征中，微信广告投放金额和商品销售额的相关性比较高。因此，为了简化模型，我们将暂时忽略微博广告和其他类型广告投放金额这两组特征，只留下微信广告投放金额数据。这样，就把多变量的回归分析简化为单变量的回归分析。

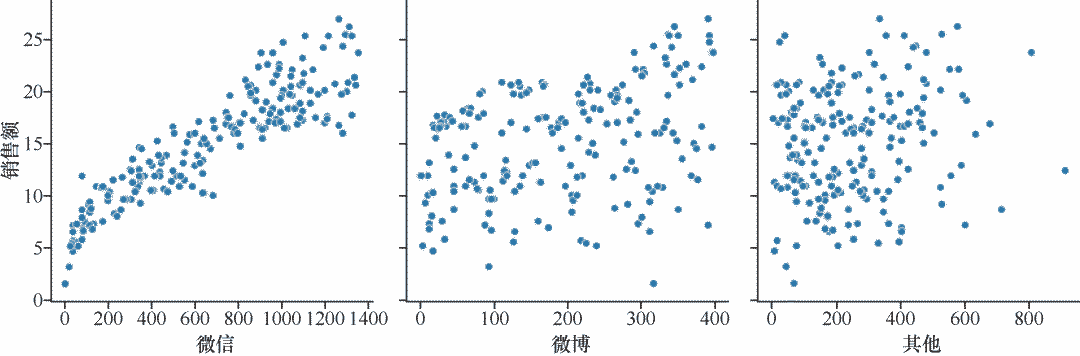
数据集清洗和规范化

下面的代码把df_ads 中的微信公众号广告投放金额字段读入一个NumPy 数组X ，也就是清洗了其他两个特征字段，并把标签读入数组y ：

X = np.array(df_ads.wechat) # 构建特征集, 只含有微信公众号广告投放金额一个特征
y = np.array(df_ads.sales) # 构建标签集, 销售额
print (" 张量X 的阶:", X.ndim)
print (" 张量X 的形状:", X.shape)
print (" 张量X 的内容:", X)

对于回归问题的数值类型数据集，机器学习模型所读入的规范格式应该是2D张量，也就是矩阵，其形状为 （样本数，标签数）。其中的行是数据，而其中的列是特征。大家可以把它想象成Excel表格的格式。

那么就现在的特征张量X而言，则是要把它的形状从（200，） 变成（200，1），然后再进行机器学习。因此需要用reshape 方法给上面的张量变形：

X = X.reshape((len(X), 1)) # 通过reshape 方法把向量转换为矩阵, len 函数返回样本个数
y = y.reshape((len(y), 1)) # 通过reshape 方法把向量转换为矩阵, len 函数返回样本个数
print (" 张量X 的阶:", X.ndim)
print (" 张量X 的形状:", X.shape)
print (" 张量X 的内容:", X)

经过整理的特征数据集可以被机器学习模型所读取。

拆分数据集为训练集和测试集

在开始建模之前，还需要把数据集拆分为两个部分：「训练集」和「测试集」。

在普通的机器学习项目中，至少要包含这两个数据集，一个用于训练机器，确定模型，另一个用于测试模型的准确性。不仅如此，往往还需要一个验证集，以在最终测试之前增加验证环节。目前这个问题比较简单， 数据量也少，我们简化了流程，合并了验证和测试环节。

这两个数据集需要随机分配，两者间不可以出现明显的差异性。因此，在拆分之前，要注意数据是否已经被排序或者分类，如果是，还要先进行打乱。

Sklearn 中的train_test_split 函数，是机器学习中拆分数据集的常用工具。使用下面的代码段将数据集进行80%（训练集）和20%（测试集）的分割。

# 将数据集进行80%( 训练集) 和20%( 测试集) 的分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=0)

其中的random_state参数，则用于数据集拆分过程的随机化设定。如果指定了一个整数，那么这个数叫作随机化种子，每次设定固定的种子能够保证得到同样的训练集和测试集，否则进行随机分割。

把数据归一化

为了让机器在读取数据的时候感觉更“舒服”，训练起来效率更高，还需要进行特征的缩放。特征缩放的方法，包括标准化、数据的压缩（也叫归一化），以及规范化等。

这里就对数据进行归一化。归一化是按比例的线性缩放。数据归一化之后，数据分布不变，但是都落入一个小的特定区间，比如0 ～ 1 或者-1 ～ +1。

下面定义一个归一化函数：

def scaler(train, test): # 定义归一化函数, 进行数据压缩
min = train.min(axis=0) # 训练集最小值
max = train.max(axis=0) # 训练集最大值
gap = max - min # 最大值和最小值的差
train -= min # 所有数据减去最小值
train /= gap # 所有数据除以最大值和最小值的差
test -= min # 把训练集最小值应用于测试集
test /= gap # 把训练集最大值和最小值的差应用于测试集
return train, test # 返回压缩后的数据

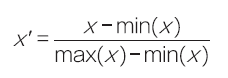
并调用此函数对数据集做特征缩放，其实就是压缩数据。

X_train, X_test = scaler(X_train, X_test) # 对特征归一化
y_train, y_test = scaler(y_train, y_test) # 对标签也归一化

至此，对数据准备、分析，包括简单的特征工程工作已经全部完成，下面进入机器学习建模与 训练机器的关键环节。

回归模型的选择和建立

选择线性回归模型

刚才咱们已经绘制出了微信和销售额的散点图。根据这个散点图手工绘制一条线，大概如下图所示的样子，这显示出微信公众号广告投放金额和销售额的线性关系。虽然图中的函数直线并未精确无误地穿过每个点，但已经能够反映出特征（也就是微信公众号广告投放金额）和标签（也就是 商品销售额）之间的关系，拟合程度还是挺不错的。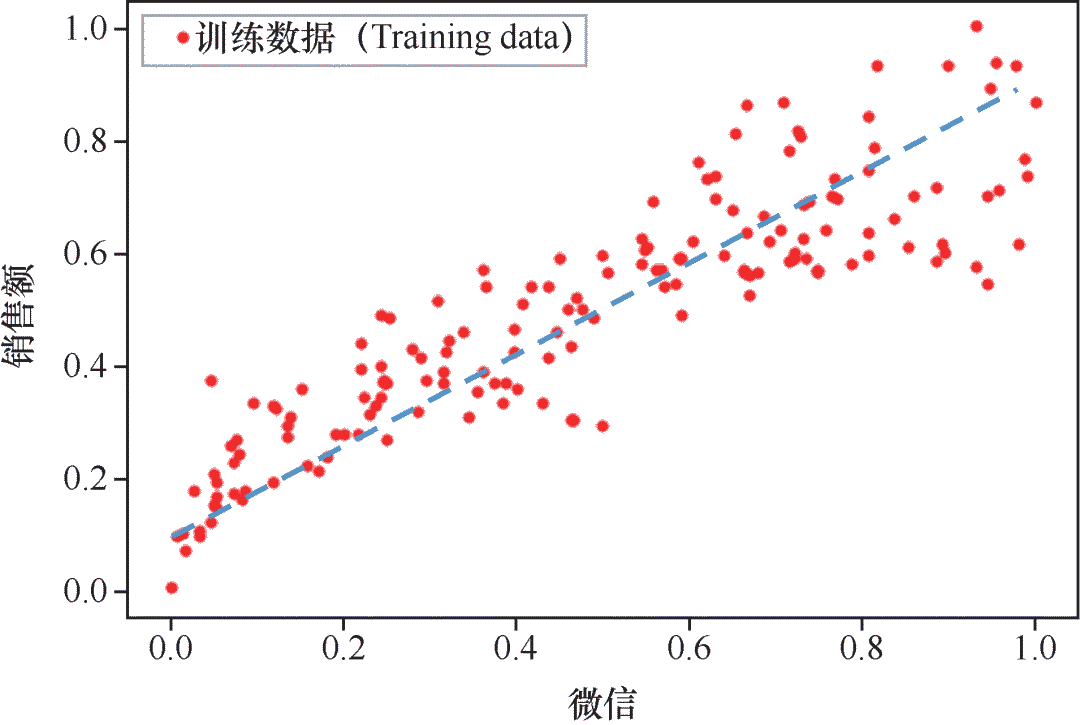这个线性函数斜率和截距的最佳值是多少呢？这还需要在机器学习的过程中才能具体确定。

这个简单的模型就是一元线性函数（如右图所示）：y=ax+b 其中，参数a的数学含义是直线的斜率（陡峭程度），b 则是截距（与y轴相交的位置）。在机器学习中，会稍微修改一下参数的代号，把模型表述为：y=wx+b 此处，方程式中的a变成了w，在机器学习中，这个参数代表「权重」。因为在多元变量（多特征） 的情况下，一个特征对应的w参数值越大，就表示权重越大。而参数b在机器学习中称为「偏置」。

定义假设函数

这个y=wx+b，在机器学习中就叫做「假设函数（hypothesis function）」，也叫「预测函数」。它负责实现预测、分类等功能。当参数W和B被确定之后，这个函数模型也就被确定了。不要小看这个简单的线性函数，在后续的机器学习过程中，此函数会作为一个基本运算单元 反复地发挥威力。

有些机器学习教程中，用 θ（读作 theta）表示机器学习的参数，也会使用 θ 0 和 θ 1 来代表此处的 w 和 b，还有用其他字母表示机器学习参数的情况。我觉得此处使用 w 和 b 来表示这些参数会使它们的意义更清晰一些：weight 是权重，bias 是偏置，各取首字母。

# 定义线性回归的预测函数
def predict(weight,bias,X): # 定义预测函数
    y_hat = weight*X + bias # 这是假设函数,其中已经应用了Python的广播功能
    return y_hat # 返回预测分类的结果

定义损失函数

下面这段代码是定义了线性回归模型的「损失函数（loss function）」。

# 定义线性回归的损失函数
def cost_function(X, y, w, b): # 手工定义一个MSE均方误差函数
    y_hat = w*X + b # 这是假设函数,其中已经应用了Python的广播功能
    loss = y_hat-y # 求出每一个y’和训练集中真实的y之间的差异 
    cost = np.sum(loss**2)/len(X) # 这是均方误差函数的代码实现
    return cost # 返回当前模型的均方误差值

那么什么是损失？它是对糟糕预测的惩罚，同时也就是对假设函数好坏的度量。「损失也就是误差，也称为成本或代价」。名字虽多，但都是一个意思，也就是当前预测值和真实值之间的差距的体现。它是一个数值，表示对于单个样本而言模 型预测的准确程度。如果模型的预测完全准确，则损失为0；如果不准确，就有损失。

在机器学习中，我们追求的当然是比较小的损失。不过，模型好不好还不能仅看单个样本，而是要针对所有 数据样本找到一组平均损失“较小”的函数模型。样本的损失的大小，从几何意义上基本上可以理解为y和y'之间的几何距离。平均距离越大，说明误差越大，模型越离谱。下图左边是平均损失较大的模型，右边是平均损失较小的模型，模型所有数据点的平均损失很明显大过右边模型。

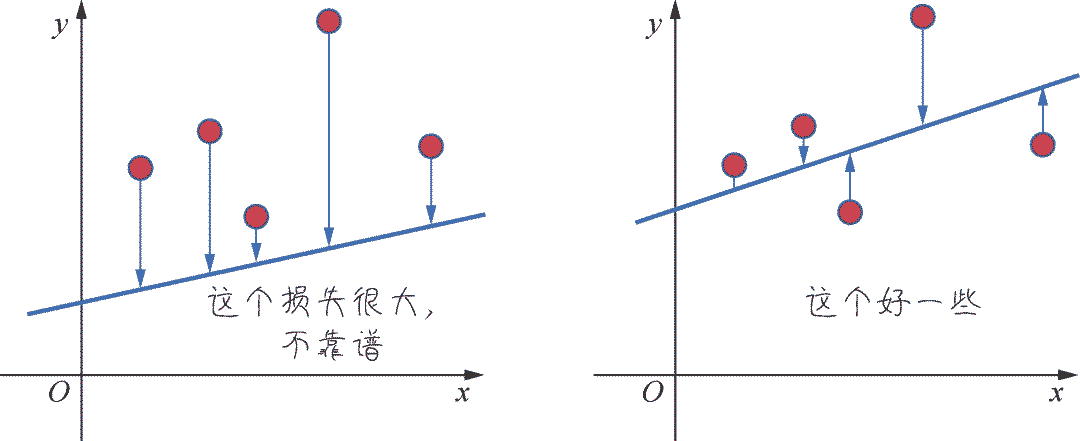
因此，针对每一组不同的参数，机器都会针对样本数据集算一次平均损失。计算平均损失是 每一个机器学习项目的必要环节。损失函数L（w，b）就是用来计算平均损失的。好那么我们胡乱猜测一组WB参数带来的损失如下

print ("当权重5，偏置3时，损失为：", cost_function(X_train, y_train, w=5, b=3))
print ("当权重100，偏置1时，损失为：", cost_function(X_train, y_train, w=100, b=1))

• 当权重5，偏置3时，损失为：25.592781941560116

• 当权重100，偏置1时，损失为：3155.918523006111

上面的误差，是通过均方误差函数计算而来。

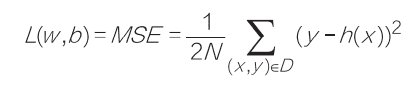
均方误差函数，也成为MSE，我们这里不展开讲它的细节，大家知道它是计算损失的一种方法即可。使用MSE函数做损失函数的线性回归算法，有时被称为最小二乘法。

如何找出最佳的W和B？梯度下降

那么现在最大的问题来了，刚才这个权重和偏置都是我们随便猜的。那么如何通过机器学习算法自动确定最佳的W和B值？

答案是：梯度下降。「梯度下降可以说是整个机器学习的精髓，堪称机器学习之魂。在我们身边发生的种种机器学习和深度学习的奇迹，归根结底都是拜梯度下降所赐。」

下面这段代码是线性回归模型实现的核心代码，正是通过梯度下降的方法来找到最佳参数值。

# 线性回归的梯度下降实现

def gradient_descent(X, y, w, b, lr, iter): # 定义一个实现梯度下降的函数
    l_history = np.zeros(iterations) # 初始化记录梯度下降过程中损失的数组
    w_history = np.zeros(iterations) # 初始化记录梯度下降过程中权重的数组
    b_history = np.zeros(iterations) # 初始化记录梯度下降过程中偏置的数组                      
    for iter in range(iterations): # 进行梯度下降的迭代，就是下多少级台阶
        y_hat  = w*X + b # 这个是向量化运行实现的假设函数
        loss = y_hat-y # 这是中间过程,求得的是假设函数预测的y和真正的y值之间的差值
        derivative_weight = X.T.dot(loss)/len(X)*2 # 对权重求导，len(X)就是数据集样本数N
        derivative_bias = sum(loss)*1/len(X)*2 # 对偏置求导，len(X)就是数据集样本数N
        w = w - lr*derivative_weight # 结合下降速率alpha更新权重
        b = b - lr*derivative_bias # 结合下降速率alpha更新偏置
        l_history[iter] = cost_function(X, y, w,b) # 梯度下降过程中损失的历史 
        w_history[iter] = w # 梯度下降过程中权重的历史
        b_history[iter] = b # 梯度下降过程中偏置的历史
    return l_history, w_history, b_history # 返回梯度下降过程数据

梯度下降的过程就是在程序中一点点变化参数w和b，使L，也就是损失值，逐渐趋近最低点（也称为机器学习中的最优解）。这个过程经常用“下山”来比喻 ：想象一个小猴子站在一座山的山腰上，正在寻找一条下山的路，这时你环望四周，找到一个最低点并向那个方向迈出一步；接着再环望四周，朝最低点方向再迈出一步……一步接一步，走到最低点。

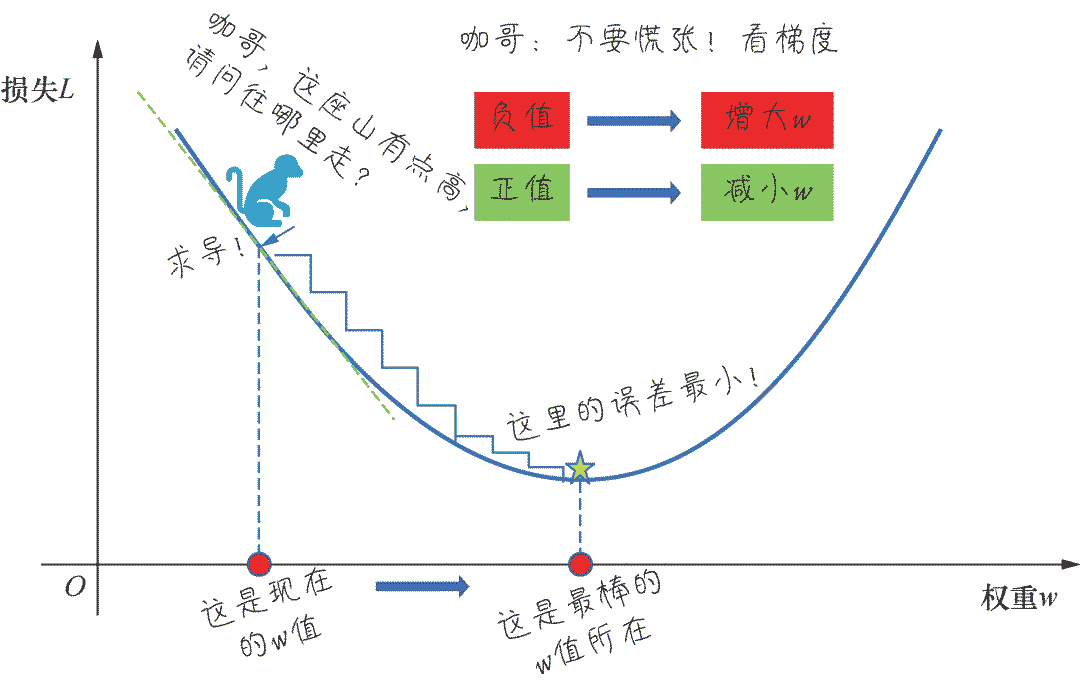
梯度下降得以实现的秘密武器是导数。

导数描述了函数在某点附近的变化率（L 正在随着w 增大而增大还是减小），而这正是进一步猜测更好的权重时所需要的全部内容。程序中用梯度下降法通过求导来计算损失曲线在起点处的梯度。此时，梯度就是损失曲线导数的矢量，它可以让我们了解哪个方向距离目标“更近”或“更远”。

• 如果求导后梯度为正值，则说明L 正在随着w 增大而增大，应该减小w，以得到更小的损失。

• 如果求导后梯度为负值，则说明L 正在随着w 增大而减小，应该增大w，以得到更小的损失。

关于学习速率

最关键的问题已经通过求导的方法解决了，我们知道权重w 应该往哪个方向走。下一个要解释的地方是小猴子应该以多快的速度下山。这在机器学习中被称为「学习速率」（learning rate）的确定。学习速率也记作α ，读作alpha。

学习速率乘以损失曲线求导之后的微分值，就是一次梯度变化的步长（step size）。它控制着当前梯度下降的节奏，或快或慢，w将在每一次迭代过程中被更新、优化。

如果所选择的学习速率过小，机器就会花费很长的学习时间，需要迭代很多次才能到达损失函数的最底点，如下面左图所示。相反，如果学习速率过大，导致L的变化过大，越过了损失曲线的最低点，则下一个点将永远在U形曲线的底部随意弹跳，损失可能越来越大，如下面右图所示。在机器学习实战中，这种损失不仅不会随着迭代次数减小，反而会越来越大的情况时有发生。

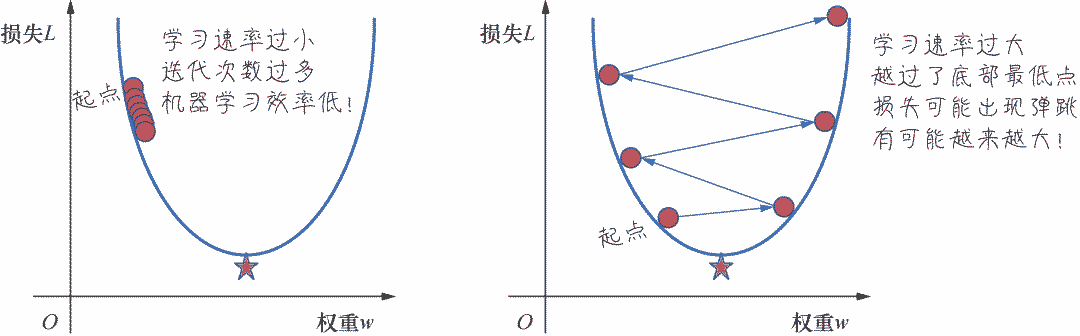
最佳学习速率与具体问题相关。因为在不同问题中，损失函数的平坦程度不同。如果我们知道损失函数的梯度较小，则可以放心地试着采用更大的学习速率，以补偿较小的梯度并获得更大的步长。

寻找最佳学习速率很考验经验和感觉。一个常见的策略是，在机器学习刚刚开始的时候，学习速率可以设置得大一些，快速几步达到靠近最佳权重的位置，当逐渐地接近最佳权重时，可以减小学习速率，防止一下子越过最优值。

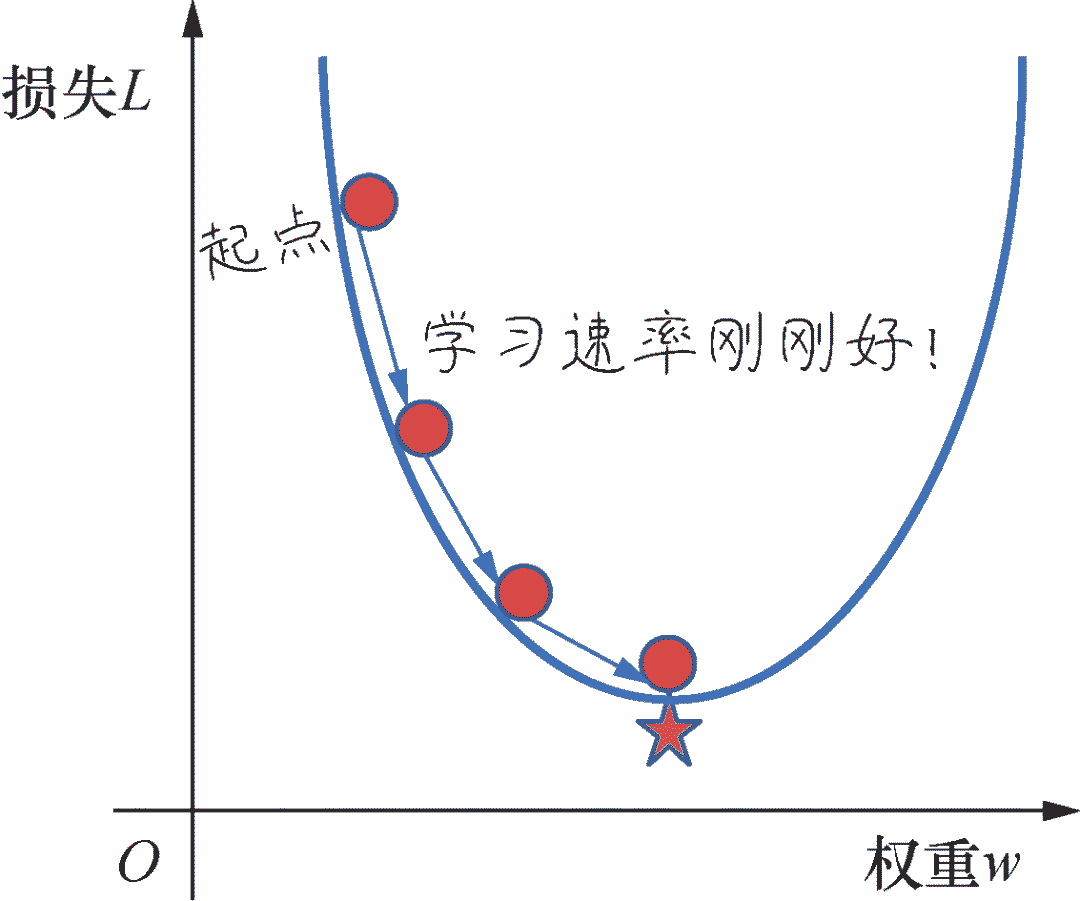
学习速率，结合着另外一个参数，「迭代次数」(iteration)，也就是梯度下降多少次最合适。就是在调试线性回归模型时，所需要确定的内容。学习速率和迭代次数这种需要手工调试的参数，我们把它们成为「超参数」，与梯度下降过程中自动确定的模型内部参数权重w和偏置b相对应。

封装线性回归模型

好了，现在一切就绪，我们会将线性回归模型封装在一个函数中。这个函数中的关键步骤就是调用梯度下降的代码。同时也将实现一些预测和预测准确率的计算。

# 定义线性回归模型 - 核心就是调用梯度下降
def linear_regression(X, y, weight, bias, alpha, iterations): 
    loss_history, weight_history, bias_history = gradient_descent(X, y, 
                                                                  weight, bias, 
                                                                  alpha, iterations)
    print("训练最终损失:", loss_history[-1]) # 打印最终损失
    y_pred = predict(weight_history[-1],bias_history[-1],X) # 预测
    traning_acc = 100 - np.mean(np.abs(y_pred - y))*100 # 计算准确率
    print("线性回归训练准确率: {:.2f}%".format(traning_acc))  # 打印准确率
    return loss_history, weight_history, bias_history # 返回训练历史记录

后面的训练机器并调参的过程中，我们将调用该线性回归模型。

训练机器，调试参数

函数的初始状态

权重和偏置的初始值的选择可以是随机的，这对结果的影响不大，因为我们知道无论怎么选择，梯度下降总会带领机器“走”到最优结果（差别只是步数的多少而已）。因此我们先随机指定几个参数，看一看现在的损失值大小，以及初始的函数状态如何。

通过下面的代码设置初始参数值：

# 首先确定参数的初始值
iterations = 500; # 迭代1500次
alpha = 0.5; #学习速率设为1,0.5和0.01，分别试一下
weight = -5 # 权重
bias = 3 # 偏置
# 计算一下初始权重和偏置值所带来的损失
print ('当前损失：',cost_function(X_train, y_train, weight, bias))

上面的代码设定各个参数的初始值并通过损失函数loss_function，求出初始损失：

• 当前损失：1.343795534906634

通过下面的代码绘制当前函数模型：

# 绘制当前的函数模型
plt.plot(X_train, y_train,'r.', label='Training data') # 显示训练集散点图
line_X = np.linspace(X_train.min(), X_train.max(), 500) # X值域
line_y = [weight*xx + bias for xx in line_X] # 假设函数y_hat
plt.plot(line_X,line_y,'b--', label='Current hypothesis' ) # 显示当前拟合函数
plt.xlabel('Wechat Ads') # x轴Label
plt.ylabel('Sales') # y轴Label
plt.legend() # 显示图例
plt.show() # 显示绘图

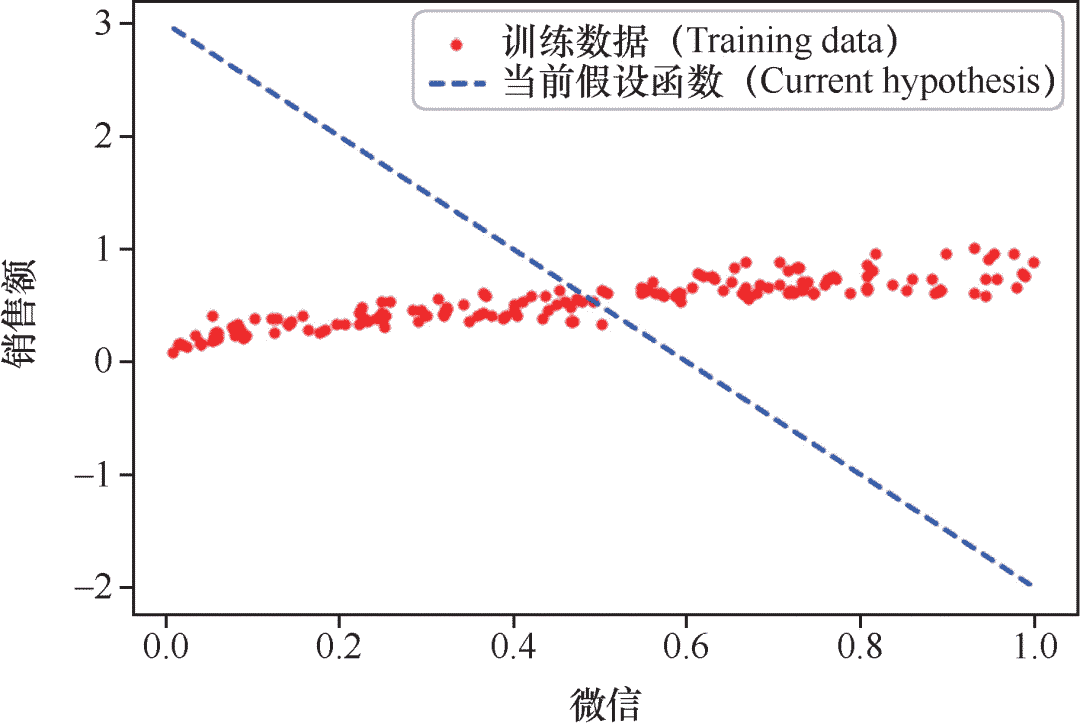
不难发现，当前这个拟合结果显得很离谱，因为初始权重和偏置的值都是随机选择的，我故意选择很大的误差值，目的就是在后面的步骤中更好地显示出梯度下降的效果。”

训练机器，发现最佳参数

下面就基于损失比较大的初始模型，进行梯度下降，也就是开始训练机器，拟合函数。

调用刚才已经定义好的梯度下降函数gradient_descent，并迭代500次（在上面参数初始化的代码中已设定好的），也就是下500 级台阶：

# 用线性回归模型训练机器，拟合函数
loss_history, weight_history, bias_history = \
   linear_regression(X_train,y_train,weight,bias,alpha,iterations)

我们可以绘制出梯度下降过程中的损失曲线

plt.plot(loss_history,'g--',label='Loss Curve')
plt.xlabel('Iterations') # x轴Label
plt.ylabel('Loss') # y轴Label
plt.legend() # 显示图例
plt.show() # 显示损失曲线

在迭代过程中，损失曲线将呈现一个下降的趋势。曲线显示，迭代100次，还没有完全收敛，500次之后，损失值基本上将不在改变。

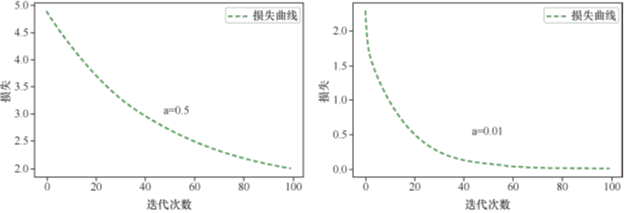
当训练机器过程中的超参数学习速率和迭代次数都设置的比较合适时，我们会发现损失值逐渐收敛，此时我们绘制当前的线性函数图像，会显示出比较漂亮的拟合图像。

此时，我们打印出模型的参数，也就是权重和偏置：

print ('当前权重：',weight_history[-1])
print ('当前偏置：',bias_history[-1])

• 当前权重：0.6608381748731955

• 当前偏置：0.17402747570052432

这也就是我们的机器所习得的线性回归函数 ：「y' =0.66x +0.17」

在测试集上验证模型

虽然已经得到了针对训练集的最佳线性回归函数模型，但是，我们的机器学习项目并没有做完，下面还有非常非常关键的一步：「在测试集上对刚才的模型进行验证」。

如果验证出来的效果并不理想，说明这个模型只针对训练数据有效，是不能被泛化到训练集之外的数据中去的。还要返工重新训练。

下面我们看一看当前模型在测试集上的损失值：

print ('测试集损失：',cost_function(X_test, y_test, weight_history[-1], bias_history[-1]))

结果显示，在测试集上的损失值为：0.009068113079114393

用下面的代码，我们同时绘制训练集和测试集损失曲线：

# 同时绘制训练集和测试集损失曲线
loss_test ,a , b = gradient_descent(X_test, y_test, weight, bias, alpha, iterations)
plt.plot(loss_history,'g--',label='Traning Loss Curve')
plt.plot(loss_test,'r',label='Test Loss Curve')
plt.xlabel('Iterations') # x轴Label
plt.ylabel('Loss') # y轴Label
plt.legend() # 显示图例
plt.show()

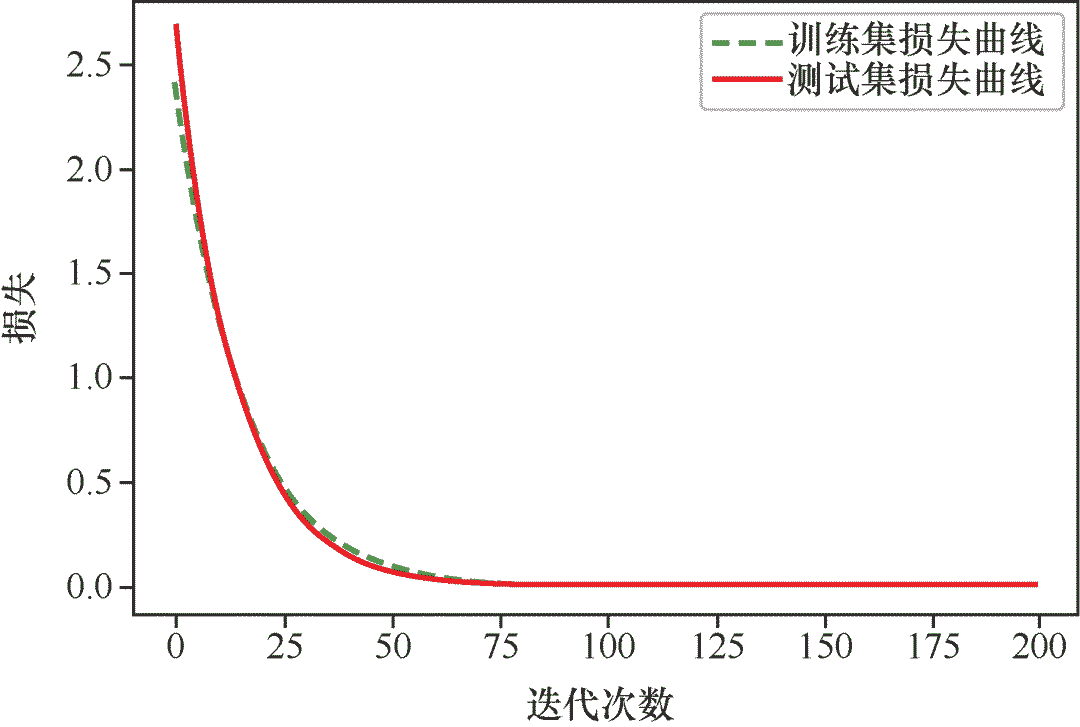
在曲线中看出，测试集与训练集的损失随迭代次数的增加，呈现相同的下降趋势，说明我们的机器学习模型是成功的。在训练的初期，训练集上的损失明显小于测试集上的损失，但是这种差距会随着学习的过程而逐渐变小，这也是机器学习过程正确性的体现。因此，最终确定了一个适合预测小冰的网店销售额的最佳线性回归模型：

函数：「y' =0.66x +0.17」

而我们刚才所做的全部工作，就是利用机器学习的原理，基于线性回归模型，通过梯度下降， 找到了两个最佳的参数值而已。

下图形象的绘制出梯度下降过程中损失逐渐减小，函数拟合成功的过程。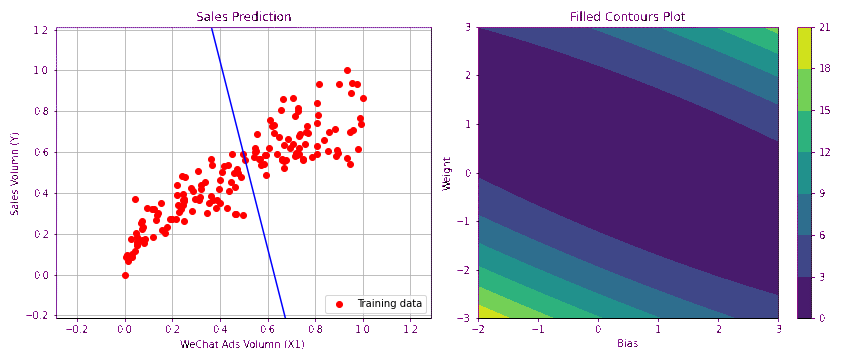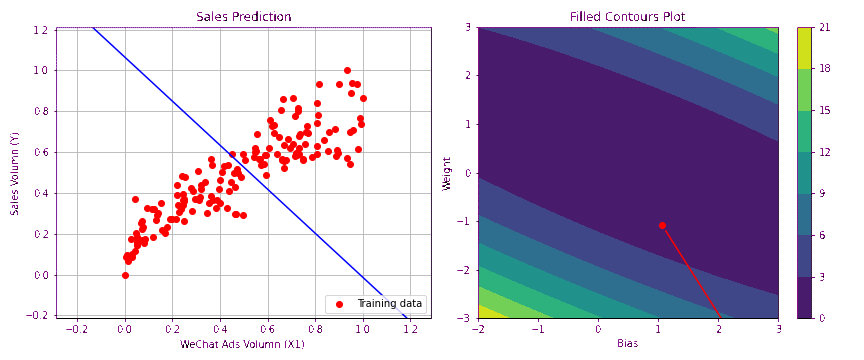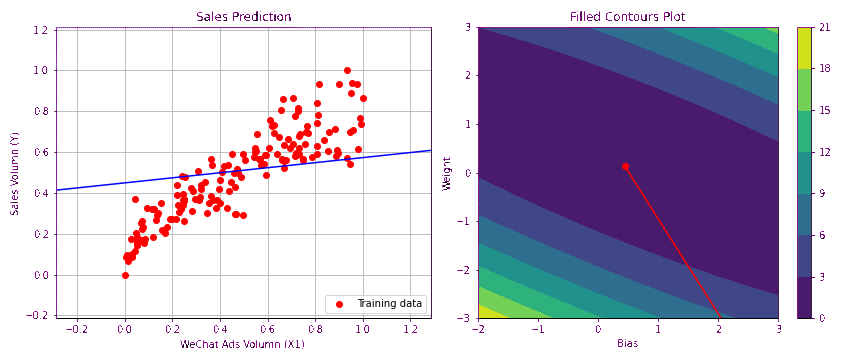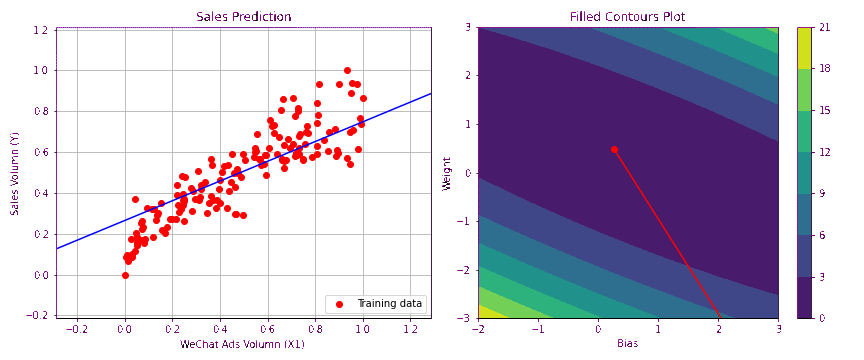

「至此，一个简单的线性回归机器学习实战项目成功结束！」

❝

本书通过AI“小白”小冰拜师程序员咖哥学习机器学习的对话展开，内容轻松，实战性强，主要包括机器学习快速上手路径、数学和Python基础知识、机器学习基础算法（线性回归和逻辑回归）、深度神经网络、卷积神经网络、循环神经网络、经典算法、集成学习、无监督和半监督等非监督学习类型、强化学习实战等内容，以及相关实战案例。

❞

参考阅读：《零基础学机器学习》https://item.jd.com/12763913.html

本文代码和数据获取方式：点击阅读原文即可前往获取。

扫码回复：2021  获取最新学习资源

加群 加入Python学习交流群

▲点击上方卡片，一起学Python

学习更多：
整理了我开始分享学习笔记到现在超过250篇优质文章，涵盖数据分析、爬虫、机器学习等方面，别再说不知道该从哪开始，实战哪里找了

“点赞”传统美德不能丢