【C语言王者实战训练营】第二期·修炼递归与迭代

本篇内容摘要

本期训练营讲解函数递归和迭代在一些经典算法问题中的应用。

本篇前言

递归与迭代共同的特点就是都会重复的进行某个操作，所以我们使用它们首先心里就得有“重复”这个概念。

递归的意思就是A重复调用A，是一种“大事化小，小事化了”的思路，也就是说我们不要一上来就想着解决问题，而是先把大问题剥离成一个次大的问题和一个小问题，再把次大的问题剥离成一个次次大的问题和一个小问题，最终剥出了一个最简单的问题，然后所有问题都迎刃而解。就像是在剥洋葱一样，先剥一层，再剥一层，层层递进，最终解决问题。

迭代就是循环，循环是指A不断调用B，目的就是在一个函数里直接完成任务。由于计算机强大的计算能力，所以我们不要在乎问题看起来有多庞大，我们在乎的是这个任务能不能被简单但是不断重复的操作完成。比如让我们从一数到一亿，这对人来说很烦，但是对计算机来说就不是问题。所以我们要具备计算机的思维，看清楚问题的难点到底在哪。

“百无一用是书生”，实战演练现在开始。

---

---

斐波那契数问题

问题描述

斐波那契数列是这样一个数列：这个数列前两项是1，从第三项开始，每一项都等于前两项之和。
根据定义这个数列的通项公式可以写成：$$a_n=a_{n-1}+a_{n-2}$$我们需要做的是编写程序求第n个斐波那契数。

思路分析

由于$a_n$的通项公式就是一个递归的公式，所以第一时间想到的就是用递归的写法来做这题，而且直接在程序中复现公式即可。

思路转化成代码

设求第n个斐波那契数的函数是Fib（英文Fibonacci的缩写），那递归的部分就是return Fib(n-1)+Fib(n-2);，同时千万不要忘记写递归的限制条件，否则就是死递归程序会报错。观察发现n = 3时，n - 2 =1，所以n<=2时，跳出递归；n<=2时，$a_n$为1，所以return 1;

#include
int Fib(int n)
{
     
	if (n <= 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}
int main()
{
     
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);
}

算法优化

这种这种递归的写法看起来语法简单，思路清晰，而且确实能解决问题，但它其实是一种效率极低的程序。当我们想知道第1000个斐波那契数的时候，博主的电脑跑了10分钟。为什么会这么慢呢？因为我们如果想知道第1000个斐波那契数，至少需要进行2¹⁰⁰⁰次运算，因为每层递归都会裂变成两个递归，不断的裂变，就会产生指数爆炸型的运算量。而且前文我们说过，递归还存在栈溢出的问题，说不定放到别的电脑上运行，程序就栈溢出了。所以这种算法是非常不合适的。

迭代的好处就是只会申请一个函数的空间，所以基本上不用担心以上的问题。递归能解决的问题往往有相应的迭代做法。这次我们就使用迭代的做法来优化算法。我们先把迭代的程序写出来，再分析它到底在哪里做出了优化。
那怎么用迭代来写斐波那契数呢，迭代的思路就是A不断执行B，所以我们需要找到每次计算中不断重复执行的部分。我们发现每次计算下一个$a_n$时，$a_{n-1}$就是上一个$a_n$；$a_{n-2}$就是上一个$a_{n-1}$，如图所示：

所以每次的计算实际上是进行了一个交换。如果设$a_n$为c，$a_{n-1}$为b，$a_{n-2}$为a，那么每轮计算，就是将b的值赋给a，c的值赋给b，a+b的值赋给c，c就是本轮计算的结果。

#include
int Fib(int n)
{
     
	int a = 1;
	int b = 1;
	int c = 1;
	int i = 1;
	while (i <= n-2)
	{
     
		c = a + b;
		a = b;
		b = c;
		i++;
	}
	return c;
}
int main()
{
     
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);
}

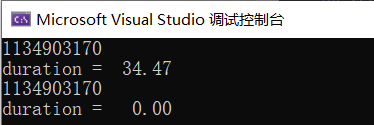
结果同样是正确的。

我们来计算一下同一个n的情况下这两个程序的运行时间：

#include
#include
#include
clock_t start, stop;
double duration;
int Fib1(int n)
{
     
	if (n <= 2)
		return 1;
	else
		return Fib1(n - 1) + Fib1(n - 2);
}
int Fib2(int n)
{
     
	int a = 1;
	int b = 1;
	int c = 1;
	int i = 1;
	while (i <= n-2)
	{
     
		c = a + b;
		a = b;
		b = c;
		i++;
	}
	return c;
}
int main()
{
     
	int n = 45;
	//使用递归法
	start = clock();
	int ret1 = Fib1(n);
	printf("%d\n", ret1);
	stop = clock();
	duration = ((double)(stop - start)) / CLK_TCK;
	printf("duration = %6.2lf\n", duration); 
	//使用迭代法
	start = clock();
	int ret2 = Fib2(n);
	printf("%d\n", ret2);
	stop = clock();
	duration = ((double)(stop - start)) / CLK_TCK;
	printf("duration = %6.2lf\n", duration);
	return 0;
}

duration的单位是秒，我们n仅仅是45的时候递归法就用了34.47秒，而迭代法甚至没有达到1毫秒（所以显示的数据是0）。不同的算法的运行时间竟然差了几万倍，这是由于n=45时，递归需要执行2⁴³次，而迭代只需要执行43次。现在，你知道优化算法的重要性了吗？

斐波那契数问题还有许多实际应用的场景，其中之一是青蛙跳台阶问题，感兴趣的同学可以自行研究一下。

---

逆序排列字符串问题

---

问题描述

输入一串字符，然后将字符串的内容逆序排列（注意不是逆序打印），且不允许使用任何C字符串库函数。
例如：输入字符串为“abcd”，改变后的字符串内容为“dcba”。

---

思路分析

逆序排列的一种思路是把元素依次取出然后再逆序放回，这样的话我们可能得创建另一个中间数组来存储取出的字符，而且如果有n个字符就得重复执行n次操作。这里直接给出更优的思路：逆序问题优先考虑首尾交换的方法，比如dcba实际上就是将abcd的首尾（ad）交换然后再将剩下的首尾（bc）交换，这样n个字符至多只需要n/2次操作，速度快了整整一倍。

---

思路转化成代码

首尾交换可以用中间变量赋值实现；不断缩进字符串可以用之前说过的left和right变量确定左右边界字符然后left++,right- -；不允许使用字符串库函数就自己写一个my_strlen

#include
int my_strlen(char* x)
{
     
	if (*x == '\0')
	{
     
		return 0;
	}
	else
	{
     
		return 1 + my_strlen(x + 1);
	}
}
void reverse_string(char a[],int len)
{
     
	char tmp = 0;
	int left = 0;
	int right = len - 1;
	while (left < right)
	{
     
		tmp = a[left];
		a[left] = a[right];
		a[right] = tmp;
		left++;
		right--;
	}
}
int main()
{
     
	char arr[100] = {
      0 };
	scanf("%s", &arr);
	reverse_string(arr,my_strlen(arr));
	printf("%s", arr);
}

虽然问题已经解决了，但是如果有一天题目硬性规定必须用递归写，我们也应该会写。
其实这个问题可以拆解成每次交换首尾+剩余字符串的逆序：

#include
int my_strlen(char* x)
{
     
	if (*x == '\0')
	{
     
		return 0;
	}
	else
	{
     
		return 1 + my_strlen(x + 1);
	}
}
void reverse_string(char a[])
{
     
	int len = my_strlen(a);
	char tmp = 0;
	if (len <= 1)
	{
     
		return;
	}
	else
	{
     
		tmp = a[0];
		a[0] = a[len - 1];
		a[len - 1] = '\0';
		reverse_string(a + 1);
		a[len - 1] = tmp;
	}
}
int main()
{
     
	char arr[100] = {
      0 };
	scanf("%s", &arr);
	reverse_string(arr);
	printf("%s", arr);
}

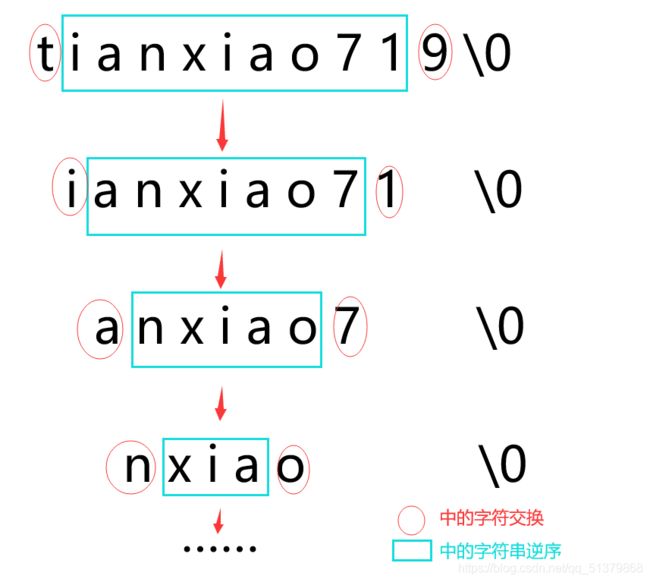
讲解一下reverse函数实现部分：

---

汉诺塔问题

名称由来和背景：【汉诺塔——百度百科】

---

问题描述

现在有三个柱子，一个柱子上有从低到高从大到小放置的圆盘，整组圆盘叫做“汉诺塔”。现在需要把一个柱子上的汉诺塔全部转移到另一个柱子上，任何状态下都得是小的在上大的在下。每次只能移动一片圆盘，移动一次相当于一个步骤。
现给出汉诺塔中的圆盘个数m，求将全塔移动到另一柱所需步骤。

---

思路分析

(递归掌握熟练的同学可以直接看总结)
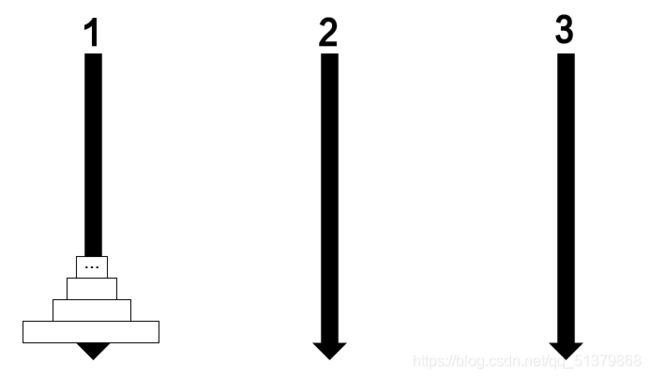
下面是m盘汉诺塔的初始状态：

下面是m盘汉诺塔的最终状态：

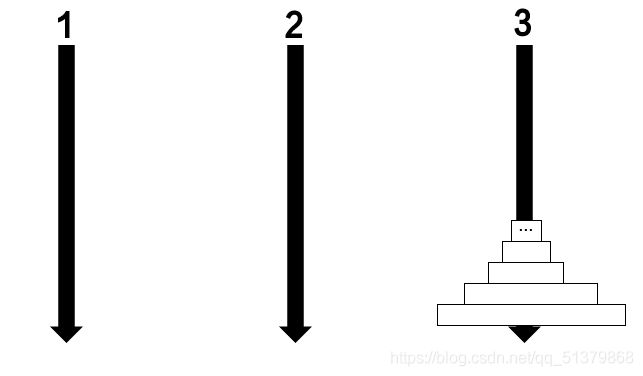
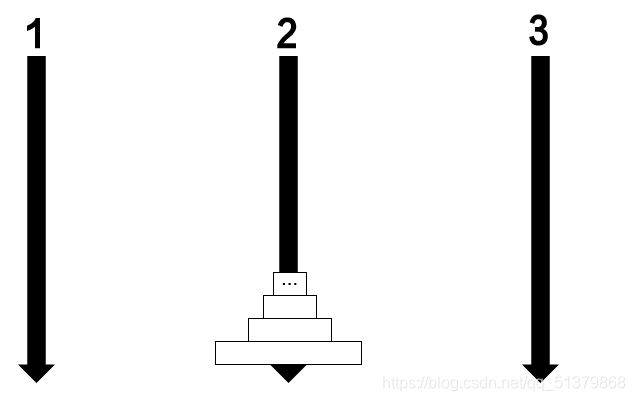
由于柱3放置的第一块圆盘一定是最大的那个（第m个），所以最终情况前，一定有这样的中间状态：

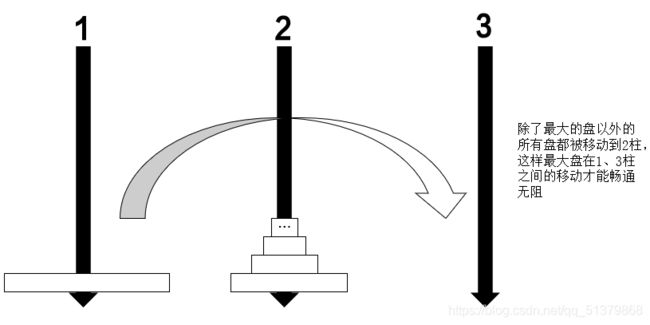
我们把这个状态记作①，把①后的下一个状态记作②：

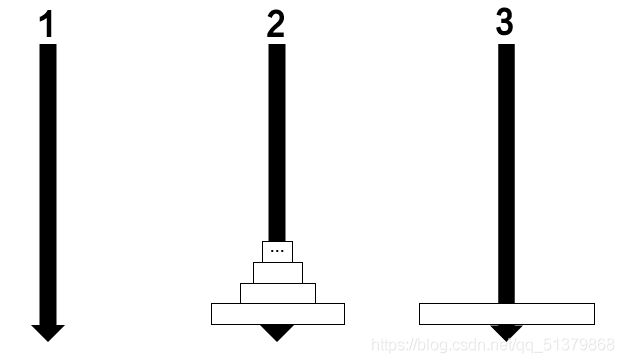
我们发现：
①状态和初始状态中间差了一个操作：就是如何将m-1层汉诺塔从1柱移动到2柱
①和②之间差了一个操作：就是把第m层圆盘从1柱移动到3柱
②状态和最终状态之间差了一个操作：就是如何将m-1层汉诺塔从2柱移动到3柱
由于m-1层汉诺塔从1柱移动到2柱和从2柱移动到3柱的步骤是等效的，所以问题就变成了解决2¹个m-1层汉诺塔的问题。
这就实现了问题的递归转化（熟练的小伙伴可能已经知道怎么解这道题了，我再往后讲几步）。
那如何解决m-1层汉诺塔问题呢？

对于m-1层汉诺塔，它的初始状态是这样的：

它的最终状态是这样的：

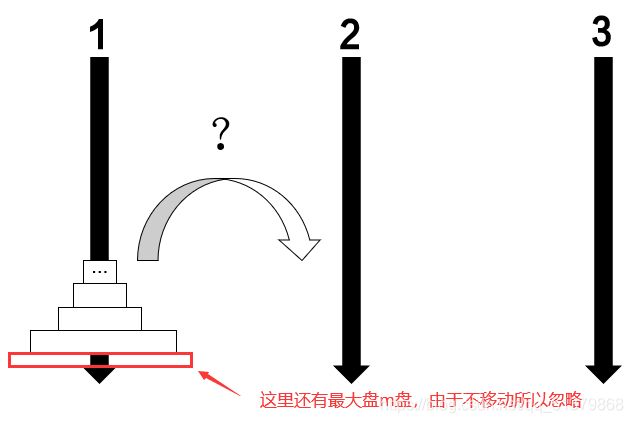
由于柱2放置的第一块圆盘一定是最大的那个（第m-1个），所以它之前肯定有这样一种中间状态：

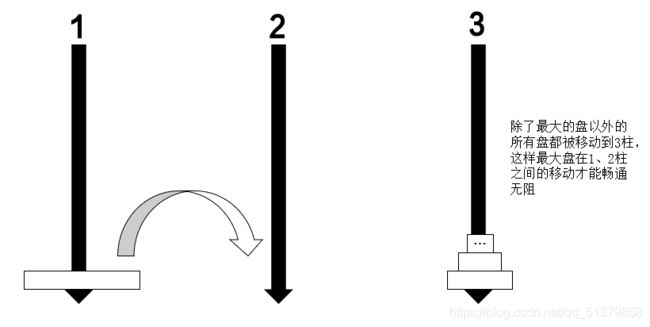
我们把这个状态记作①，把下一个状态记作②：

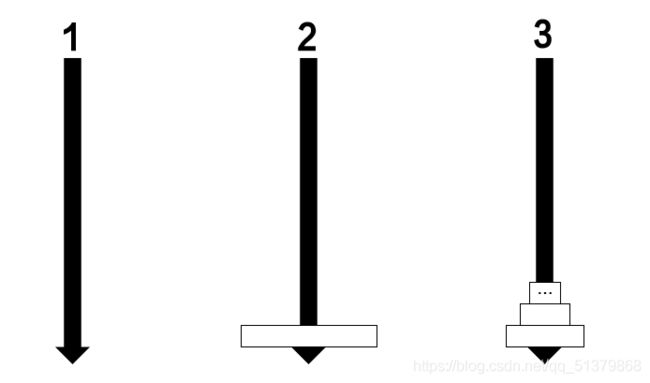
我们发现：
①状态和初始状态中间就差了一个操作：就是如何将m-2层汉诺塔从1柱移动到3柱
①和②之间差了一个操作：就是把第m层圆盘从1柱移动到2柱
②状态和最终状态之间也差了一个操作：就是如何将m-2层汉诺塔从3柱移动到2柱
由于m-2层汉诺塔从1柱移动到3柱和从3柱移动到2柱的步骤是等效的，所以问题就变成了解决2²m-2层汉诺塔的问题。
… …
如此一来我们可以一直把问题转化成1层汉诺塔问题，而一层汉诺塔问题是很好解决的。这样m层汉诺塔问题就迎刃而解了。
同时，每层汉诺塔问题都会裂变成两个小汉诺塔问题：

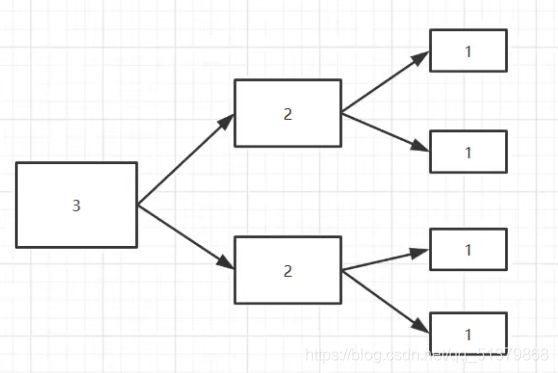
我们可以总结出规律：解决m层汉诺塔问题至少需要2^m-1步。

---

总结

解决m层汉诺塔问题可以归纳成以下三步：
1：把m-1层汉诺塔从1柱移动到2柱
2：把第m层圆盘从1柱移动到3柱
3：把m-1层汉诺塔从2柱移动到3柱


解决m层汉诺塔问题至少需要2^m-1步。

---

思路转化成代码

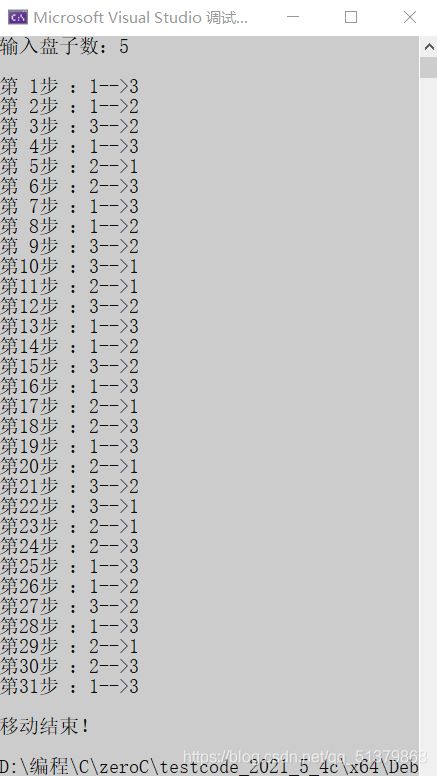
我们只要根据思路的三个步骤写出递归代码即可（下面代码中Hanoi函数的else部分）。编写move函数让每一步的操作可视化（我是用文字描写的这部分，感兴趣的同学可以研究怎么用动画写这部分）。编写Hanoi函数实现递归。move函数中引入static变量k，这样可以记录我们的总步骤数。

#include 
void Hanoi(int n, char x, char y, char z)
{
     
    void move(char, int, char);
    if (n == 1)
        move(x, 1, z);
    else
    {
     
        Hanoi(n - 1, x, z, y);
        move(x, n, z);
        Hanoi(n - 1, y, x, z);
    }
}
void move(char start, int n, char end)
{
     
    static int k = 1;
    printf("第%2d步 ：%c-->%c\n", k, start, end);
    k++;
}
int main()
{
     
    int n, counter;
    printf("输入盘子数：");
    scanf("%d", &n);
    printf("\n");
    Hanoi(n, '1', '2', '3');
    printf("\n");
    printf("移动结束！\n");
    return 0;
}

---

求最大子列和问题

---

问题描述

现有一整数数列，求其子数列中，各元素的和最大的子数列，并输出这个子数列的和。

---

一般我们会想到的思路是遍历所有子数列，求最大子列和，我给出代码：

int MaxSubseqSum1(int A[], int N)
{
     
    int ThisSum, MaxSum = 0;
    int i, j, k;
    for (i = 0; i < N; i++) 
    {
      /* i是子列左端位置 */
        for (j = i; j < N; j++) {
      /* j是子列右端位置 */
            ThisSum = 0;  /* ThisSum是从A[i]到A[j]的子列和 */
            for (k = i; k <= j; k++)
                ThisSum += A[k];
            if (ThisSum > MaxSum) /* 如果刚得到的这个子列和更大 */
                MaxSum = ThisSum;    /* 则更新结果 */
        } /* j循环结束 */
    } /* i循环结束 */
    return MaxSum;
}

这种方法确实能解决问题，但是它的时间复杂度是O(f(n²))，不算是一个很高效算法。下面介绍两种较为高效的算法：

递归思路：分而治之——分治法

什么叫分治法呢。就是先把数列从中间分成两部分，然后求左边数列的最大子列和，再求右边数列的最大子列和，然后再求跨边界的数列的最大子列和，然后三者做比较，得出最大子列和。
比如数列-2 1 4 -7，如果将-2 1看作左列，4 -7看作右列，那左列的最大子列和是-2 1 -1三者最大值就是1，右列的最大子列和是4 -7 -3三者最大值也就是4，但是不论是4还是1都不是整个数列的最大子列和，因为还存在跨边界的最大子列和。跨边界的最大子列和是从边界开始向左和向右扫描得到的最大子列和：

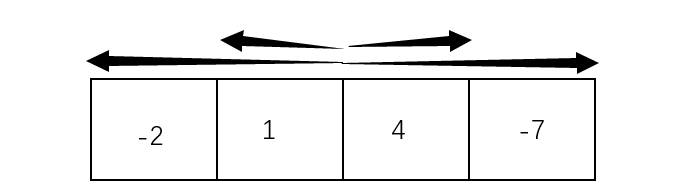
向左扫面第一个元素是1，所以当前最大值是1，再向左扫描到-2，1和-2的和小于1所以不更新最大值，然后向右扫描的第一个元素是4，4和1的和是5大于1所以更新最大值为5，再向右扫描扫到-7，5和-7的和小于5所以停止扫描，得到跨边界最大子列和为5。
跨边界最大子列和5、左列最大子列和1、右列最大子列和4三者中5最大，所以整个数列的最大子列和是5

由这种方法可以求得数列4 -3 5 -2 -1 2 6 -2的最大子列和为11

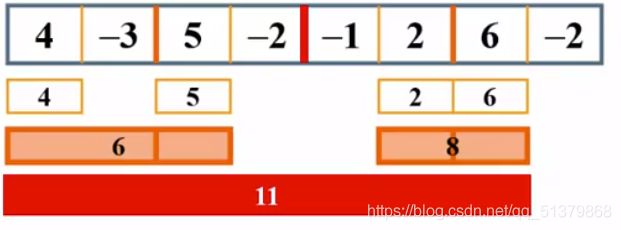
给出代码（附带讲解注释）：

int Max3(int A, int B, int C)
{
      /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}

int DivideAndConquer(int List[], int left, int right)
{
      /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/

    int LeftBorderSum, RightBorderSum;
    int center, i;

    if (left == right) {
      /* 递归的终止条件，子列只有1个数字 */
        if (List[left] > 0)  return List[left];
        else return 0;
    }

    /* 下面是"分"的过程 */
    center = (left + right) / 2; /* 找到中分点 */
    /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer(List, left, center);
    MaxRightSum = DivideAndConquer(List, center + 1, right);

    /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for (i = center; i >= left; i--) {
      /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if (LeftBorderSum > MaxLeftBorderSum)
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */

    MaxRightBorderSum = 0; RightBorderSum = 0;
    for (i = center + 1; i <= right; i++) {
      /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if (RightBorderSum > MaxRightBorderSum)
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */

    /* 下面返回"治"的结果 */
    return Max3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);
}

---

迭代思路：拥新弃旧——更新法

迭代的思路是一种很巧妙的思路，因为我们发现。如果一个子列扩张时扩进了一个负数，那这个子列的和必然减小，所以负数是我们需要舍弃的“旧元素”，正数是我们需要拥抱的“新元素”
给出代码：

int MaxSubseqSum4(int A[], int N)
{
     
    int ThisSum, MaxSum;
    int i;
    ThisSum = MaxSum = 0;
    for (i = 0; i < N; i++)
    {
     
        ThisSum += A[i];
        if (ThisSum > MaxSum)
            MaxSum = ThisSum;
        else if (ThisSum < 0)
            ThisSum = 0;
    }
    return MaxSum;
}

---

更新法的时间复杂度（O(n)）明显小于分治法（O(n · log(n))），所以更新法是一种更优的算法。但是这两种算法思想都极为经典，我们都应该好好学习揣摩。

---

本篇涉及知识：
【C语言从青铜到王者】第二篇·详解函数
【C语言从青铜到王者】第三篇·详解数组