【人脸识别】基于PCA+LDA实现人脸识别matlab 源码
一、简介
1 PCA
1.1 数据降维
降维的方法包括:主成分分析(PCA)、因子分析(FA)、和独立成分分析(ICA)
主成分分析:寻找向量,使各个样本到该向量的投影之和最小。
因子分析:
独立成分分析:
1.2 PCA:目的是降维,降维的实际原理是最大化目标函数(数据投影后的方差最大)
强推原理博文:https://blog.csdn.net/fendegao/article/details/80208723
(1)假设有m个n维样本: {Z1,Z2,…,Zm}
(2)样本中心 u 为: 所有样本观测值之和/(mxn)
(3)去中心化后,得到矩阵 {X1,X2,…,Xm}={Z1-U,Z2-U,…,Zm-U}
(4)记含有n个元素的向量W,则样本X1在w方向上的投影为二者内积 X1 . W
(5)PCA的目标函数为最大化投影
目标方程可以化为矩阵形式求解,求解方法:
(1)构建拉格朗日算子,求导为0,解得投影最大的向量为特征值最大对应的特征向量。
根据特征值的累计贡献率可以指定选取多少个W向量作为K-L变换矩阵。若选择了4个主成分,则对于每一个n维度样本,经过矩阵变换后,都变为了(1xn)x(nx4)=1x4维向量,即达到了降维的目的。
(2)SVD奇异值分解:降维只需求出右奇异矩阵,即AA(T)的特征向量,不需要求A的协方差矩阵。对内存友好。
1.3 基于PCA的人脸识别
(1)基于人脸样本库,例如现实中人脸拍照(银行、车站)等数据采集方法,建立人脸库。
(2)求取训练人脸库的协方差阵的特征值和特征向量。
(3)对于需要判别的人脸,判断其在特征向量上的投影与哪个训练样本的投影最接近。
!!!注::需要注意,协方差矩阵是维度之间的协方差,故是nxn维,但是在实际应用时,例如图像降维(假设一幅图像有200*10个像素,有100幅图像),一个像素就是一个维度,则原本协方差阵XX’为 (2000x100)x (100x2000)维,计算机存储计算消耗过大,此时可以考虑使用替代矩阵P=X’X(100x2000)x(2000x100)替代: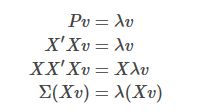
P的特征值即原始协方差阵的特征值,P的特征向量左乘数据矩阵即为原始协方差阵的特征向量。
2 LDA
LDA:线性判别分析,也称为Fisher线性判别,是常用的降维技术。
基本思想:将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。
LDA降维后的维度是直接和类别的个数相关的,与数据本身的维度没关系,比如原始数据是n维的,一共有C个类别,那么LDA降维之后,维数取值范围为(1,C-1),举个例子,假设图像分类,两个类别正例反例,每个图像用10000维特征表示,那么LDA之后,就只有1维特征,并且这维特征的分类能力最好。
对于很多两类分类的情况,LDA之后就剩下1维,找到分类效果最好的一个阈值貌似就可以了。
假设,x是一个N维的列向量,要使x通过LDA降到C维,只需要找到一个投影矩阵w,也即,一个N*C的矩阵,让w的转置矩阵和x相乘,便成为C维的了。(投影在数学上的表示就是用一个矩阵去相乘)
此时,问题的关键就在于:寻找一个投影矩阵!并且,该投影矩阵要保证模式样本在新的子空间有最大的类间距离和最小的类内距离。
二、源代码
clear all
clc
close all
start=clock;
sample_class=1:40;%样本类别
sample_classnum=size(sample_class,2);%样本类别数
fprintf('程序运行开始....................\n\n');
for train_samplesize=3:8;
train=1:train_samplesize;%每类训练样本
test=train_samplesize+1:10;%每类测试样本
train_num=size(train,2);%每类训练样本数
test_num=size(test,2);%每类测试样本数
address=[pwd '\ORL\s'];
%读取训练样本
allsamples=readsample(address,sample_class,train);
%先使用PCA进行降维
[newsample base]=pca(allsamples,0.9);
%计算Sw,Sb
[sw sb]=computswb(newsample,sample_classnum,train_num);
%读取测试样本
testsample=readsample(address,sample_class,test);
best_acc=0;%最优识别率
%寻找最佳投影维数
for temp_dimension=1:1:length(sw)
vsort1=projectto(sw,sb,temp_dimension);
%训练样本和测试样本分别投影
tstsample=testsample*base*vsort1;
trainsample=newsample*vsort1;
%计算识别率
accuracy=computaccu(tstsample,test_num,trainsample,train_num);
if accuracy>best_acc
best_dimension=temp_dimension;%保存最佳投影维数
best_acc=accuracy;
end
end
%---------------------------------输出显示----------------------------------
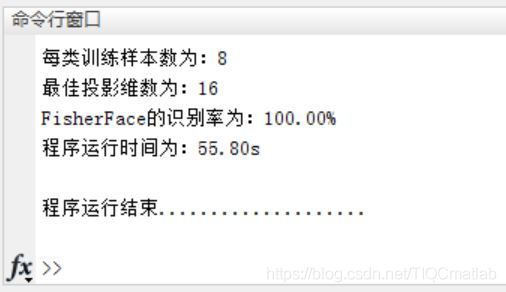
fprintf('每类训练样本数为:%d\n',train_samplesize);
fprintf('最佳投影维数为:%d\n',best_dimension);
fprintf('FisherFace的识别率为:%.2f%%\n',best_acc*100);
fprintf('程序运行时间为:%3.2fs\n\n',etime(clock,start));
end
function [newsample basevector]=pca(patterns,num)
%主分量分析程序,patterns表示输入模式向量,num为控制变量,当num大于1的时候表示
%要求的特征数为num,当num大于0小于等于1的时候表示求取的特征数的能量为num
%输出:basevector表示求取的最大特征值对应的特征向量,newsample表示在basevector
%映射下获得的样本表示。
[u v]=size(patterns);
totalsamplemean=mean(patterns);
for i=1:u
gensample(i,:)=patterns(i,:)-totalsamplemean;
end
sigma=gensample*gensample';
[U V]=eig(sigma);
d=diag(V);
[d1 index]=dsort(d);
if num>1
for i=1:num
vector(:,i)=U(:,index(i));
base(:,i)=d(index(i))^(-1/2)* gensample' * vector(:,i);
end
else
sumv=sum(d1);
for i=1:u
if sum(d1(1:i))/sumv>=num
l=i;
break;
end
end
for i=1:l
vector(:,i)=U(:,index(i));
base(:,i)=d(index(i))^(-1/2)* gensample' * vector(:,i);
end
end
function sample=readsample(address,classnum,num)
%这个函数用来读取样本。
%输入:address就是要读取的样本的地址,classnum代表要读入样本的类别,num是每类的样本;
%输出为样本矩阵
allsamples=[];
image=imread([pwd '\ORL\s1_1.bmp']);%读入第一幅图像
[rows cols]=size(image);%获得图像的行数和列数
for i=classnum
for j=num
a=imread(strcat(address,num2str(i),'_',num2str(j),'.bmp'));
b=a(1:rows*cols);
b=double(b);
allsamples=[allsamples;b];
end
end
三、运行结果
四、备注
完整代码或者代写添加QQ1575304183