【搞定左神算法初级班】第6节:前缀树、贪心算法
目 录:
一、前缀树:Prefix Tree
1.1 前缀树题目举例:一个字符串类型的数组 arr1,另一个字符串类型的数组 arr2
1.2 前缀树的 insert、delete、search、prefixNum 方法
二、贪心算法
题目1:按最低字典序拼接字符串
题目2:切分金条总代价最小
题目3:最多做 K 个项目的最大利润
题目4:安排最多的宣讲场次
一、前缀树:Prefix Tree
- 前缀树又叫字典树、Trie 树,单词查找树或键树,是一种多叉树结构。
- 前缀树的功能很强大,比如有一个字符串数据,我们要从查找其中以“hell”开头的(设置一个passN),或者以"ive"结尾的字符的个数等等操作。我们只需要在定义前缀树的时候加上相应得数据项就可以了。
- 建议:字母用边表示,不要塞到节点里【具体看代码实现】。
1.1 前缀树题目举例:一个字符串类型的数组 arr1,另一个字符串类型的数组 arr2
题目1、 arr2中有哪些字符,是arr1中出现的?请打印。
- 返回树中有多少个要求查找的单词 public int search(String word) 的变体。
题目2、arr2中有哪些字符,是作为arr1中某个字符串前缀出现的?请打印。
- 有多少单词以pre为前缀 public int prefixNumber(String pre)的变体。
题目3、arr2中有哪些字符,是作为arr1中某个字符串前缀出现的?请打印arr2中出现次数最大的前缀。
- 有多少单词以pre为前缀 public int prefixNumber(String pre),找最大的个。
1.2 前缀树的 insert、delete、search、prefixNum 方法
- 几种方法的代码相似度很高,前半部分基本一样,都是从 root 开始遍历;
-
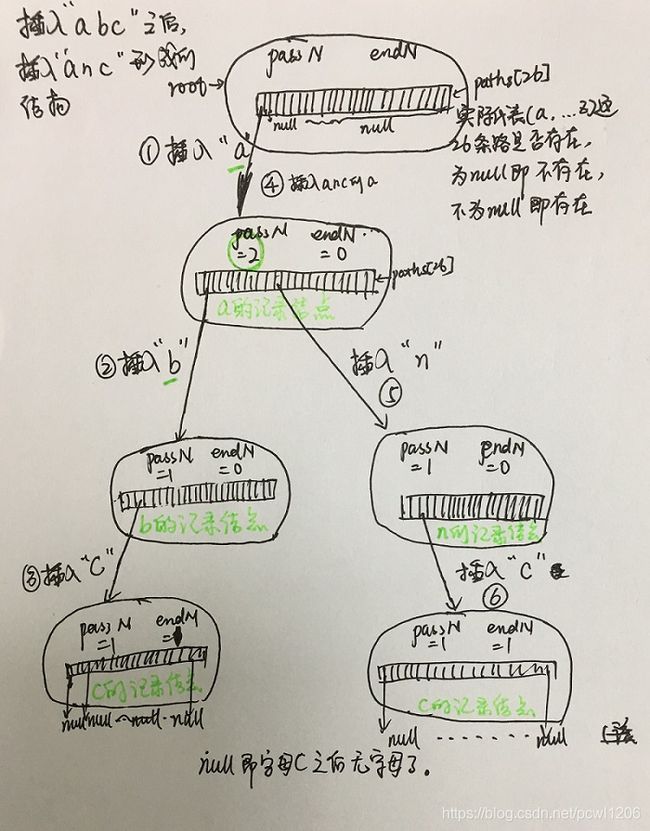
假设刚开始我们,有一个空节点,现在我们有一个操作,往这个空的节点上insert字符串“abc”, 那么我们按照下面的步骤insert:
-
process: 1、首先看当前节点有没有指向字符'a'的路径,没有的话就创建指向'a'的路径,否则滑过到下一个字符,同样是看看有没有到该字符的路径。一直遍历完字符,并且都创建好了路径。如下图所示:
- 代码实现
package com.offer.foundation.class5;
/**
* @author pengcheng
* @date 2019/3/29 - 22:34
* @content: Trie树的基本操作的实现
*/
public class TrieTree {
public static class TrieNode{
private int passNum; // 表示有多少个字符串经过该节点
private int endNum; // 表示有多少个字符串以该节点结尾
private TrieNode[] paths; // 存储的是该节点到下一级所有节点的路径是否存在
public TrieNode(){
passNum = 0;
endNum = 0;
paths = new TrieNode[26]; // 假设只有26个小写字母,即每一个节点拥有26条可能的路径
}
}
private TrieNode root; // 不管什么操作,都是从根节点开始的,所以要记录根节点
public TrieTree(){
// Trie树的初始化
root = new TrieNode();
}
// 往trie树中插入一个字符串
public void insert(String word){
if(word == null){
return;
}
char[] chars = word.toCharArray();
TrieNode node = root;
int index = 0; // index值:0-25 对应 a-z
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a'; // 计算该字符在当前节点的那条路径上
// 判断该路径是否已经存在
if(node.paths[index] == null){
node.paths[index] = new TrieNode(); // 如果路径不存在,则创建它
}
// 路径已经存在的话,就继续向下走
node = node.paths[index];
node.passNum++; // 划过当前节点的字符串数+1
}
node.endNum++; // 遍历结束了,记录下以该字母结束的字符串数+1
}
// 删除一个字符串
public void delete(String word){
// 删除之前,先判断有没有
if(search(word) == 0){
return;
}
char[] chars = word.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a';
// 注意 --
if(--node.paths[index].passNum == 0){
// 如果遍历到某个节点时,将其index处passNum减1后等于0,则说明没有其他字符串经过它了,直接将其设置为null
node.paths[index] = null;
return;
}
node = node.paths[index]; // 继续向下遍历
}
node.endNum--; // 遍历完了,删除了整个单词,则将以该单词最后一个字符结尾的字符串的数目减1
}
// 在trie树中查找word字符串出现的次数
public int search(String word){
if(word == null){
return 0;
}
char[] chars = word.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a';
if(node.paths[index] == null){
return 0; // 不存在
}
node = node.paths[index]; // 到达了该字母记录的节点路径,继续往下走
}
// 整个单词的所有字母都在树中,说明单词在树中,返回该单词最后一个字符的endNum
return node.endNum;
}
// 返回有多少单词以pre为前缀的
public int prefixNum(String pre){
if(pre == null){
return 0;
}
char[] chars = pre.toCharArray();
TrieNode node = root;
int index = 0;
for(int i = 0; i < chars.length; i++){
index = chars[i] - 'a';
if(node.paths[index] == null){
return 0; // 不存在
}
node = node.paths[index]; // 继续向下找
}
return node.passNum; // 找到pre最后一个字符的passNum值
}
}
二、贪心算法
你自己想出贪心策略,但只能感觉它对不对,理论证明放弃吧!重点在于想很多的贪心策略,用对数器去证明对不对。
- 所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择(最小,最大,最优等等)。也就是说,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。
- 贪心策略适用的前提是:局部最优策略能导致产生全局最优解。 【不要去理论证明你选择的贪心策略的正确性,因为太复杂,你最好直接看结果对不对就好】
- 贪心算法的基本思路:
- 1.建立数学模型来描述问题;
- 2.把求解的问题分成若干个子问题;
- 3.对每一子问题求解,得到子问题的局部最优解;
- 4.把子问题的解局部最优解合成原来解问题的一个解。
题目1:按最低字典序拼接字符串
- 题目:给定一个字符串类型的数组strs,找到一种拼接方式,使得把所有字符串拼起来之后形成的字符串具有最低的字典序。
- 字典序:对于两个字符串
- 长度不一样,将短的个补0(0是最小ASCII码值),补成长度一样;
- 先按首字符排序,如果首字符相同,再按第二个字符排序,以此类推。如aa,ab,ba,bb,bc就是一个字典序,从小到大。
- 【分析】贪心:你定一个指标,按这个指标来,对每个样本分出个优先,优先级大的先处理,优先级小的后处理。
- 本题的贪心策略就是你选择的比较策略
- str1.str2 <= str2.str1,则 str1 放前面,否则 str2 放前面【根据两个字符串拼接的结果的大小来决定排序】,不能直接根据str1和str2的大小比较决定位置排放,比如:b和ba,最小的字典序应该是bab而不是bba。
- 本题的贪心策略就是你选择的比较策略
package com.offer.foundation.class5;
import java.util.Arrays;
import java.util.Comparator;
/**
* @author pengcheng
* @date 2019/3/30 - 10:53
* @content: 贪心策略:按最低字典序拼接字符串
*/
public class Lowest {
// 自定义比较器:给字符串按照自定义的规则排序
public class MyComparator implements Comparator {
@Override
public int compare(String a, String b) {
return (a + b).compareTo(b + a); // 哪个小哪个放前面
}
}
public String getLowestString(String[] strs){
if(strs == null || strs.length == 0){
return "";
}
// 给字符串数组按照自己定义的规则排序
// 对于制定的贪心策略,先直观分析下对不对,不要去试图证明,可以使用对数器证明
Arrays.sort(strs, new MyComparator());
String res = "";
for (String str : strs) {
res += str;
}
return res;
}
// 测试
public static void main(String[] args) {
Lowest lowest = new Lowest();
String[] str = {"ba", "b","baa"}; // baabab
System.out.println(lowest.getLowestString(str));
}
}
题目2:切分金条总代价最小
题目:一块金条切成两半,是需要花费和长度数值一样的铜板的。比如:长度为20的金条,不管切成长度多大的两半,都要花费20个铜板。一群人想整分整块金条,怎么分最省铜板?
例如:给定数组{10, 20, 30},代表一共三个人,整块金条长度为 10+20+30=60. 金条要分成10, 20, 30三个部分。 如果, 先把长度60的金条分成10和50,花费60,再把长度50的金条分成20和30,花费50,一共花费110铜板。
但是如果先把长度60的金条分成30和30,花费60,再把长度30金条分成10和20,花费30 一共花费90铜板。
输入一个数组,返回分割的最小代价。
- 【分析】:贪心:每次合并代价最小的,设总代价为 cost = 0
- 1)把数组的元素放入优先队列(小根堆)中;
- 2)每次弹出最小的两个数【使其代价最小,因为贪心算法就是局部最优】,然后相加的结果为 c,总代价加上 c,并且将 c 放入堆中;
- 3)重复1)、2)步骤,直到堆中只剩有一个数结束。
- 【注意】: 优先队列是小根堆,你认为谁该在前面,就通过比较器把它的优先级设小【并不是实际数值小就在前面,也可能实际数值大在前面,看你比较器怎么弄了,返回负数:表示o1小于o2】
- 标准的霍夫曼编码问题:先选两个最小的合并,然后再往上合并(如下图所示)。合并是从下往上,切割的是从上往下:先将60切成30、30,再将其中一个30切成10、20,最后就将60切成:10、20、30
补充:堆结构的扩展与应用【经常用于贪心】:
- 堆:用于在一群数据中拿出最好的那个(根据自定义的比较器不同实现不同的堆,比较器就是贪心的标准),默认建的是小根堆(优先级小的放前面)。
package com.offer.foundation.class5;
import java.util.Comparator;
import java.util.PriorityQueue;
/**
* @author pengcheng
* @date 2019/3/30 - 11:43
* @content: 最小代价问题:实质上是霍夫曼编码问题
*/
public class LowestCost {
// 最小堆
public class MyComparator implements Comparator{
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2; // 谁小把谁放在前面: -表示o1小
}
}
// 输入的是一个数组,数组中的元素则是最终的切割方式,现在要找出这种方式需要花费的最小代价
public int lowestCost(int[] arr){
// 优先级队列是小根堆,谁在前面,就把谁的优先级设置小点
PriorityQueue pq = new PriorityQueue<>(new MyComparator());
for (int i : arr) {
pq.add(i);
}
int costTotal = 0; // 总的代价
int costOne = 0; // 两数合并的代价
// 等于1的时候,说明堆里面只有一个元素了,即已经合并完成
while(pq.size() > 1){
costOne = pq.poll() + pq.poll(); // 合并堆里面最小的两个元素
costTotal += costOne; // 两小数合并的结果
pq.add(costOne); // 将两小数合并的结果重新添加到堆里
}
return costTotal;
}
// 测试
public static void main(String[] args) {
LowestCost lc = new LowestCost();
int[] arr = {10, 20, 30, 40};
int res = lc.lowestCost(arr);
System.out.println(res); // 190 = 10 + 20 + 30 + 30 + 40 + 60
}
}
- 以后遇到类似的问题,可以考虑下是否能够用霍夫曼编码的思想去解决。
题目3:最多做 K 个项目的最大利润
题目:costs[]:花费 ,costs[i] 表示 i 号项目的花费 profits[]:利润, profits[i] 表示 i 号项目在扣除花费之后还能挣到的钱(利润)。一次只能做一个项目,最多做 k 个项目,m 表示你初始的资金。(说明:你每做完一个项目,马上获得的收益,可以支持你去做下一个项目)求你最后获得的最大钱数。
- 【分析】贪心:每次总是做能够做的项目中利润最大的。
- 准备一个小根堆和大根堆,小根堆放着全部的项目,按谁花费(成本)最低就在头部。
- 1、若小根堆不为空,项目也没做完 K 个,则每次先从小根堆解锁能够做的项目,放入大根堆(大根堆按照解锁的项目中谁的利润最大放在头部);
- 2、大根堆不为空,从大根堆弹出堆顶项目来做(即利润最大的项目,每次只弹出堆顶一个项目来做);
- 3、把 m 加上利润,初始资金增加,再重复1)、2)步骤。
举例说明:
- 注意:
- 1、解锁项目:只要项目成本在当前资金范围以内都可以被解锁,并不是一次只能解锁一个,然后按照利润的大小放进大根堆里,然后按照利润大的先做。所谓解锁项目其实就是资金肯定大于项目成本,该项目一定可以被做的,可以直观的感受下;
- 2、结束条件:可能做不到k个项目就会停了,因为可能存在成本比较高的项目,大根堆中可做的项目都做完了,总资金还是无法解锁成本比较大的项目,必须要停止了。
package com.offer.foundation.class5;
import java.util.Comparator;
import java.util.PriorityQueue;
/**
* @author pengcheng
* @date 2019/3/30 - 20:07
* @content: 贪心算法:做多做k个项目的最大利润
*/
public class IPO {
// 项目节点
public class Node{
private int profit; // 项目利润
private int cost; // 项目成本
public Node(int profit, int cost){
this.profit = profit;
this.cost = cost;
}
}
/**
* @param k :最多做k个项目
* @param fund :总的资金
* @param profits :每个项目的利润数组
* @param cost :每个项目的成本数组
* @return
*/
public int findMaxCapital(int k, int fund, int[] profits, int[] cost){
// 初始化每个项目节点信息
Node[] nodes = new Node[profits.length];
for (int i = 0; i < profits.length; i++) {
nodes[i] = new Node(profits[i], cost[i]);
}
// 优先级队列是谁小谁放在前面,比较器决定谁小
PriorityQueue minCostQ = new PriorityQueue<>(new MinCostComparator()); // 成本小顶堆
PriorityQueue maxProfitQ = new PriorityQueue<>(new MaxProfitComparator()); // 利润大顶堆
for (int i = 0; i < nodes.length; i++) {
minCostQ.add(nodes[i]); // 将所有的项目插入成本堆中
}
// 开始解锁项目,赚取利润
for (int i = 0; i < k; i++) {
// 解锁项目的前提条件:成本堆中还有项目未被解锁并且该项目的成本小于当前的总资金
while(!minCostQ.isEmpty() && minCostQ.peek().cost <= fund){
maxProfitQ.add(minCostQ.poll()); // 将当前成本最小的项目解锁
}
if(maxProfitQ.isEmpty()){
// 如果maxProfitQ为空,则说明没有当前资金能够解锁的新项目了,之前解锁的项目也做完了,即无项目可做了
return fund; // 最后的总金额
}
fund += maxProfitQ.poll().profit; // 做利润最大的项目
}
return fund; // k个项目都做完了
}
// 成本小顶堆:成本最小的在堆顶
public class MinCostComparator implements Comparator{
@Override
public int compare(Node o1, Node o2) {
return o1.cost - o2.cost;
}
}
// 利润大顶堆:利润最大的在堆顶
public class MaxProfitComparator implements Comparator{
@Override
public int compare(Node o1, Node o2) {
return o2.profit - o1.profit;
}
}
}
题目4:安排最多的宣讲场次
题目:一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间(给你一个数组,里面是一个个具体项目),你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。返回这个最多的宣讲场次。
- 贪心策略的分析:
- 贪心策略1:不能按照哪个项目开始的早先安排哪个,因为可能开始早的占用时间非常长,显然不合理;
- 贪心策略2:项目持续的时间短优先安排也不合理,因为可能存在时间短的项目时间点正好在其他两个时间长项目中间,这样因为这一个项目就会浪费掉其他两个项目,显然也是不合理的;
- 贪心策略3:按照哪个项目先结束来排。先做结束最早的项目,然后淘汰因为这个做这个项目而不能做的项目(时间冲突),依次这样去做。
package com.offer.foundation.class5;
import java.util.Arrays;
import java.util.Comparator;
/**
* @author pengcheng
* @date 2019/3/30 - 20:57
* @content: 贪心算法:安排最多的宣讲场次
*/
public class BestArrange {
public class Program{
public int start; // 项目开始时间
public int end; // 项目结束时间
public Program(int start, int end){
this.start = start;
this.end = end;
}
}
/**
* @param programs :项目数组
* @param cur :当前时间
* @return :能够安排的最大项目数
*/
public int getBestArrange(Program[] programs, int cur){
// 也可以用堆来做,都一样
Arrays.sort(programs, new ProgramComparator());
int res = 0;
for (int i = 0; i < programs.length; i++) {
// 只有当前时间早于第i个项目的开始时间时,才可以安排
if(cur <= programs[i].start){
res++; // 安排上了
cur = programs[i].end; // 当前时间推移到本次安排项目的结束时间,下个项目的开始时间必须在这个时间之后
}
}
return res;
}
// 按照项目的结束时间早来排序,即实现小根堆
public class ProgramComparator implements Comparator{
@Override
public int compare(Program o1, Program o2) {
return o1.end - o2.end;
}
}
}
- 总结:贪心策略靠的是经验,靠刷题积累经验。不要试图去证明贪心策略的正确性,可以用对数器去验证。