Python机器学习算法之支持向量机算法

1.算法起源

• 1963年，前苏联学者Vladimir N. Vapnik和Alexander Y. Lerner在研究模式识别的广义肖像算法（generalized portrait algorithm）中提出支持向量方法。
• 1964年，他们进一步建立了函数间隔（硬边距）的线性SVM。并于上世纪70年代，随着最大边距决策边界的理论研究、基于松弛变量的规划问题求解技术的出现，以及VC维的提出，SVM被逐步理论化并称为统计学习理论的重要组成部分。
• 1992年，Bernhard E. Boser，Isabelle M. Guyon和Vladimir N. Vapnik运用核技巧（kernel trick）最大化边缘平面，解决非线性分类器的方法。
• 1995年，Vladimir N.Vapnik提出了统计学习理论，较好地解决了线性不可分的问题，正式奠定了SVM的理论基础。

2.算法概述

• 支持向量机（support vector machine，SVM）是一种基于统计学习理论的监督学习算法。
• 支持向量机算法是用来解决分类问题的。作为数据挖掘领域中一项非常重要的任务，分类目前在商业上应用最多（比如：分析型CRM里面的客户分类模型、客户流失模型等，其本质都属于分类问题），而分类的目的则是构建一个分类函数或分类模型，该模型能够把数据库中的数据项映射到给定类别中的某一个，从而可以用于预测未知类别。
• 支持向量机是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器。就是在特征空间里面用某条线或某块面将训练数据集分成两类，而依据的原则就是间隔最大化，这里的间隔最大化是指特征空间里面距离分离线或面最近的点到这条线或面的间隔(距离)最大。
• 支持向量机在各个领域内的模式识别问题中都有广泛应用，包括人脸识别、文本分类、笔迹识别等。它不仅在解决小样本、非线性及高维模式识别等问题中表现出了许多特有的优势，同时在函数模拟、模式识别和数据分类等领域也取得了极好的应用效果，是机器学习最成功的算法之一。
• 支持向量机中，“支持向量”的意思就是在众多的向量点中那些能够用来划分不同类别的向量，“机”的意思就是算法

3.算法分类

• 线性可分支持向量机

  又称硬间隔支持向量机，当训练数据线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机

• 线性支持向量机

  当训练数据近似线性可分时，通过软间隔最大化，学习一个线性支持向量机

• 非线性支持向量机

  又称软间隔支持向量机，当训练数据不可分时，通过使用核技巧以及软间隔最大化，学习一个非线性支持向量机

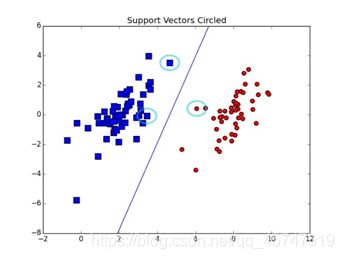
4.算法思想

1. 如上图所示，如果我们要对一种颜色和大小不同的花朵进行分类，那么此时就需要两个属性值X和Y来分别代表花朵的大小属性和颜色属性。
2. 然后我们把所有的数据都丢到 x-y 的二维平面上，接着就是要找一条直线，把这两个类别划分出来。
3. 划分后即实现了分类，以后如果预测数据的所属分类，只需要分析该数据在直线的哪一侧即可。

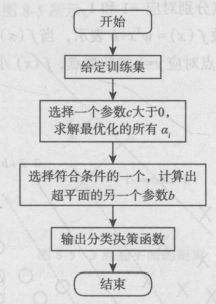
5.算法步骤

• 线性支持向量机

  

  1. 给定训练集

     

  2. 构造最优化问题，求解出最优化的所有αi

     

  3. 计算参数 w 和 b

     

  4. 得出超平面与决策函数

     

• 非线性支持向量机

  

  1. 给定训练集

     

  2. 选择一个参数 c 大于0，求解出最优化的所有αi

     

  3. 选择符合条件的一个αi ，然后计算出超平面的另外一个参数 b

     

  4. 输出分类决策函数

     

6.算法相关概念

• 线性/非线性

  线性是指量与量之间按比例，成直线关系，在数学上可理解为一阶导数为常数的函数；而非线性是指不按比例，不成直线关系，一阶导数不为常数的函数。

• 线性可分/不可分

  对于二分类问题，有那么一条直线可以把正负实例点完全分开，这些数据就是线性可分的；而线性不可分就是找不到一条直线可以把正负实例点完全分开。

• 超平面

  其实就是实例点从二维空间转移到三维甚至多维空间中，这个时候不能再用直线划分，而需要用平面去划分数据集，这个平面就称为超平面。

• 支持向量

  在线性可分的情况下，训练数据集的样本点与分离超平面距离最近的样本点称为支持向量，而支持向量机的目的就是求取距离这个点最远的分离超平面，这个点在确定分离超平面时起着决定性作用，所以把这种分类模型称为支持向量机。

• 函数间隔

  一般地，一点距离分离超平面远近程度可以反映分类预测的准确程度，在超平面wx+b=0确定的情况下，|wx+b|能够相对地表示点x距离超平面的远近。而wx+b的符号与类标记y的符号是否一致能够表示分类是否正确，所以可以用量y(wx+b)来表示分类正确性及确信度，这就是函数间隔。

• 几何间隔

  上面的函数间隔，只要成比例的改变w和b的值，超平面不会改变，但是函数间隔却会改变。比如把w和b均扩大一倍，则超平面依然是wx+b=0，而函数间隔则变成了2|wx+b|，(2wx+2b=w’x+b’=-2)。但是我们学习的目的是在保持在间隔不变的情况下通过求取间隔最大化对应的超平面来达到学习的目的，所以我们要保证w保持不变。这里对w做一些约束，如规范化，使得间隔是确定的，这时函数间隔就成了几何间隔。

• 核函数

  在线性不可分的情况下，支持向量机首先在低纬度空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。核函数的价值在于它虽然也是将特征进行从低维到高维的转换，但核函数事先在低纬上进行计算，而将实质上的分类效果表现在高维上，也就避免了直接在高维空间中的复杂计算。

7.算法实现

sklean库提供了线性分类支持向量机（LinearSVC）的实现

class sklearn.svm.LinearSVC(
    # 代表正则化参数，字符串类型“l1”或“l2”，默认参数值为“l2”
    penalty=’l2’, 
    # 代表损失函数，字符串类型“hinge”或“squared hinge”，默认参数值为“squared hinge”
    loss=’squared_hinge’, 
    # 代表是否转化为对偶问题求解，默认是True
    dual=True, 
    # 代表残差收敛条件，默认是0.0001
    tol=0.0001, 
    # 代表惩罚参数，浮点数类型
    C=1.0, 
    # 代表多类分类问题的策略，字符串类型“ovr”或“crammer_singer”，默认参数值为“ovr”。“ovr”采用one-vs-rest分类策略；“crammer_singer”采用多类联合分类策略。
    multi_class=’ovr’, 
    # 代表是否计算截距
    fit_intercept=True, 
    intercept_scaling=1, 
    # 与其他模型中参数含义一样，也是用来处理不平衡样本数据的，可以直接以字典的形式指定不同类别的权重，也可以使用balanced参数值。
    class_weight=None, 
    # 代表是否冗余，默认是0
    verbose=0, 
    # 代表随机种子的大小
    random_state=None, 
    # 代表最大迭代次数
    max_iter=1000)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs

plt.rcParams['font.family'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 创建随机分布的，可以分离的400个样本点
X, y = make_blobs(n_samples=400, centers=2, random_state=32)

# 创建线性支持向量机LinearSVC对象
clf = LinearSVC(C=10)
clf.fit(X, y)

# 画出样本点
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)

# 画出决策函数
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 网格化评价模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)

# 画出分类边界
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

plt.title("用LinearSVC实现间隔最大化分类边界")
plt.show()

7.算法优点

• 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的，所以SVM不太容易产生过拟合。

• SVM训练出来的模型完全依赖于支持向量(Support Vectors)，即使训练集里面所有非支持向量的点都被去

  除，重复训练过程，结果仍然会得到完全一样的模型。

• 一个SVM如果训练得出的支持向量个数比较小，SVM训练出的模型比较容易被泛化。

8.算法优化

• 最小二乘SVM

  SVM标准算法在应用中存在着超平面参数选择，以及问题求解中矩阵规模受训练样本数目影响很大，导致规模过大的问题。

  LS-SVM是标准SVM的一种变体，它从机器学习损失函数着手，在其优化问题的目标函数中使用二范数，并利用等式约束条件代替SVM标准算法中的不等式约束条件，使得LS-SVM方法的优化问题的求解最终变为一组线性方程组的求解。

• 概率SVM

  概率SVM可以视为逻辑回归和SVM的结合，SVM由决策边界直接输出样本的分类，概率SVM则通过Sigmoid函数计算样本属于其类别的概率。具体地，在计算标准SVM得到学习样本的决策边界后，概率SVM通过缩放和平移参数对决策边界进行线性变换，并使用极大似然估计（Maximum Liklihood Estimation, MLE）得到的值，将样本到线性变换后超平面的距离作为Sigmoid函数的输入得到概率 。