小白のKNN算法理解及代码实现

一.概述

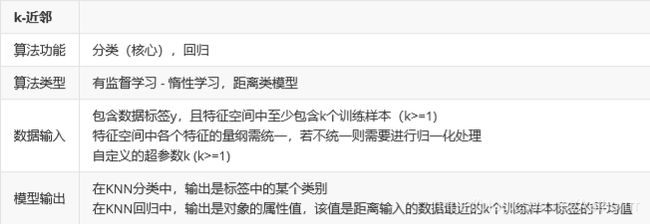
k-近邻算法（k-Nearest Neighbour algorithm），又称为KNN算法，是数据挖掘技术中原理最简单的算法。KNN的工作原理：给定一个已知标签类别的训练数据集，输入没有标签的新数据后，在训练数据集中找到与新数据最邻近的k个实例，如果这k个实例的多数属于某个类别，那么新数据就属于这个类别。可以简单理解为：由那些离X最 近的k个点来投票决定X归为哪一类。

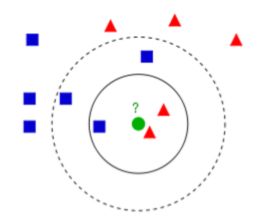
例如在这张图中绿色点进行分类，我们现有蓝色和红色两类，那具体我们分为哪一类呢？
当我们的KNN算法中K = 3 时我们可以看到取到的应该是最小圈中的三个点，而其中最多的是红色的点，固然绿色点应该分为红色类。
如果当k = 5 时取到的是最近的五个点，也就是三蓝两红，按照定义，绿色点分为蓝色。

举一个简单的镰刀书上的例子，用KNN算法分类一个电影是否是爱情片还是动作片！

在这个表中我们看到每一部电影都有相应的两个属性：打斗镜头数和接吻镜头数，我们现在要做的是根据两个属性对新电影进行分类（爱情片or动作片）。
我们在上文已经看到了KNN的工作原理，不就是根据特征值进行比较，然后提取样本集中特征最相似数据的分类标签么，那我们现在就先将表中的数据可视化看一看：

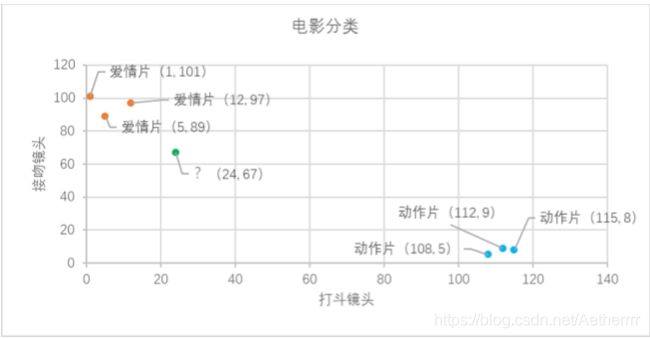
我们可以从散点图中大致推断，这个未知电影有可能是爱情片，因为看起来距离已知的三个爱情片更近一点。k-近 邻算法是用什么方法进行判断呢？没错，就是距离度量。这个电影分类例子中有两个特征，也就是在二维平面中计 算两点之间的距离，就可以用我们高中学过的距离计算公式：

如果是N维的特征值的话想必大家也会的，毕竟小学二年级知识点嘛（狗头）

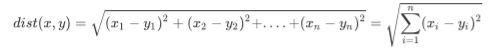
计算后的结果如下表:

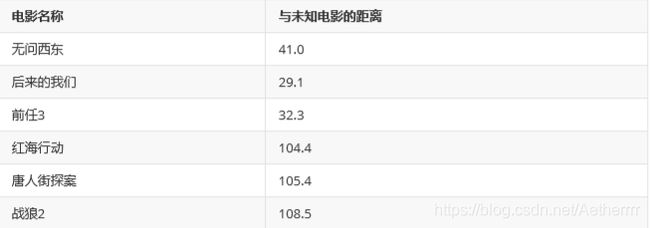
通过表2的计算结果，我们可以知道绿点标记的电影到爱情片《后来的我们》距离最近，为29.1。如果仅仅根据这 个结果，判定绿点电影的类别为爱情片，这个算法叫做最近邻算法，而非k-近邻算法。k-近邻算法步骤如下：

(1) 计算已知类别数据集中的点与当前点之间的距离； 
(2) 按照距离递增次序排序；
(3) 选取与当前点距离最小的k个点； 
(4) 确定前k个点所在类别的出现频率； 
(5) 返回前k个点出现频率最高的类别作为当前点的预测类别。

也就是说如果我们k选了个比较正常的3或者4，那么新电影就会被分类到爱情片，但如果数据量大一点，我们选的K不合理的话，那很可能就会将新电影分类到动作片，这也是这个算法的不足之处吧，我们的K取值的不同会影响最后的结果。

二.代码实现

因为上述的例子个人感觉样本过少，还是采用了镰刀书上的另一个例子：在线约会问题！
问题描述：
海伦一直使用在线约会网站寻找适合自己的约会对象，尽管约会网站会推荐不同的人选，但她并不是每一个都喜 欢，经过一番总结，她发现曾经交往的对象可以分为三类：
不喜欢的人
魅力一般的人
极具魅力得人
海伦收集约会数据已经有了一段时间，她把这些数据存放在文本文件datingTestSet.txt中，其中各字段分别为：

1. 每年飞行常客里程
2. 玩游戏视频所占时间比
3. 每周消费冰淇淋公升数

2.1 准备数据

照例写一个读入数据的函数哈：

def loaddata():
    data = pd.read_table('数据/datingTestSet.txt',header=None)
    return data

没啥好说的，耗子为之。

2.2数据可视化

我们得看看我们读入了个什么东西吧：

def draw(datingTest):
    Colors = []
    for i in range(datingTest.shape[0]):
        m = datingTest.iloc[i, -1]
        if m == 'didntLike':
            Colors.append('black')
        if m == 'smallDoses':
            Colors.append('orange')
        if m == 'largeDoses':
            Colors.append('red')

    plt.rcParams['font.sans-serif'] = ['Simhei']
    pl = plt.figure(figsize=(12, 8))
    fig1 = pl.add_subplot(221)
    plt.scatter(datingTest.iloc[:, 1], datingTest.iloc[:, 2], marker='.', c=Colors)
    plt.xlabel('玩游戏视频所占时间比')
    plt.ylabel('每周消费冰淇淋公升数')

    fig2 = pl.add_subplot(222)
    plt.scatter(datingTest.iloc[:, 0], datingTest.iloc[:, 1], marker='.', c=Colors)
    plt.xlabel('每年飞行常客里程')
    plt.ylabel('玩游戏视频所占时间比')

    fig3 = pl.add_subplot(223)
    plt.scatter(datingTest.iloc[:, 0], datingTest.iloc[:, 2], marker='.', c=Colors)
    plt.xlabel('每年飞行常客里程')
    plt.ylabel('每周消费冰淇淋公升数')
    plt.show()

运行出来是这样式儿的：

其实可以看出来类别的区间大概还是可以看不太出来的哈！

2.3数据归一化

下表是提取的4条样本数据，如果我们想要计算样本1和样本2之间的距离，可以使用欧几里得计算公式：

我们很容易发现，因为飞行里程这一项数值很大，如果计算欧几里得距离的话我们消费冰激凌数的一点点数字就会被忽略掉（冰激凌党表示气抖冷），那如何让我们的冰激凌再次崛起呢？我们这里使用到了归一化，使得这三个特征的权重相等。
数据归一化的处理方法有很多种，比如0-1标准化、Z-score标准化、Sigmoid压缩法等等，在这里我们使用最简单 的0-1标准化，公式如下：

朴实无华的代码如下:

def minmax(dataSet):
    min = dataSet.min()
    max = dataSet.max()
    normal = (dataSet - min)/(max - min)
    return normal

2.4 划分训练集和测试集

为了测试我们实现的分类器的结果，我们将原始数据分为训练集和测试集两部分，训练集用 来训练模型，测试集用来验证模型准确率。
关于训练集和测试集的切分函数，网上一搜一大堆，Scikit Learn官网上也有相应的函数比如model_selection 类中 的train_test_split 函数也可以完成训练集和测试集的切分。
通常来说，我们只提供已有数据的90%作为训练样本来训练模型，其余10%的数据用来测试模型。这里需要注意的 10%的测试数据一定要是随机选择出来的，由于海伦提供的数据并没有按照特定的目的来排序，所以我们这里可以 随意选择10%的数据而不影响其随机性。

简单的代码：

def spiltdata(dataset , rate = 0.9):
    n = dataset.shape[0]
    m = int(n * rate)
    train = dataset.iloc[ :m , :]
    test = dataset.iloc[m: , :]
    test.index =range(test.shape[0])
    return train , test

2.5 KNN分类器的实现

先上代码：

def knn(train , test , k):
    n = train.shape[1] - 1
    m = test.shape[0]
    result = []
    for i in range(m):
        dist = list((((train.iloc[ : , :n] - test.iloc[i , :n])**2).sum(1))**5)
        dist1 = pd.DataFrame({
     'dist':dist , 'lable':train.iloc[: , n]})
        d = dist1.sort_values(by='dist')[:k]
        lable_count = d.loc[ : , 'lable'].value_counts()
        result.append(lable_count.index[0])
    result = pd.Series(result)
    test['predict'] = result
    ans = (test.iloc[: , -1] == test.iloc[: , -2])
    total_num = ans.shape[0]
    ansframe = pd.DataFrame({
     'ans':ans})
    num = ansframe.sort_values(by='ans').value_counts()
    numT = num.values[0]
    return numT/total_num

n是数据集中除去标签后的列数，m为测试样本数
进入循环后我们先计算欧氏距离
dist = list((((train.iloc[ : , :n] - test.iloc[i , :n])**2).sum(1))**5)
然后将计算出来的距离和标签列合在一起，以便于之后取出最小K个的标签

dist1 = pd.DataFrame({
     'dist':dist , 'lable':train.iloc[: , n]})

之后就是简单的排序，计算个数，取出label然后添加到result中，这样我们就计算完了一个样本的分类结果，我们之后只需要全部计算完之后将计算结果与本身的label进行比较，计算出来正确率并且返回即可。

正确率达到了95% 还是很不错的！

三.总结

1.优点

1. 简单好用，容易理解，精度高，理论成熟，既可以用来做分类也可以用来做回归
2. 可用于数值型数据和离散型数据
3. 无数据输入假定
   适合对稀有事件进行分类

2.缺点

1. 计算复杂性高；
2. 空间复杂性高；
3. 计算量太大，所以一般数值很大的时候不用这个，但是单个样本又不能太少，否则容易发生误分。
4. 样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少） 可理解性比较差，无法给出数据的内在含义