论文阅读2018-10-13
论文阅读2018-10-13
- Addressing the minimum fleet problem in on-demand urban mobility 原文及翻译
- METHODS
Addressing the minimum fleet problem in on-demand urban mobility 原文及翻译
Information and communication technologies have opened the way to new solutions for urban mobility that provide better ways to match individuals with on-demand vehicles.However,a fundamental unsolved problem is how best to size and operate a fleet of vehicles,given a certain demand for personal mobility.Previous studies either do no provide a scalable solution or require changes in human attitudes towards mobility.Here we provide a network-based solution to the following ‘minimum fleet problem’, given a collection of trips (specified by origin, destination and start time), of how to determine the minimum number of vehicles needed to serve all the trips without incurring any delay to the passengers. By introducing the notion of a ‘vehicle-sharing network’, we present an optimal computationally efficient solution to the problem,as well as a nearly optimal solution amenable to real-time implementation. We test both solution on a dataset of 150 million taxi trips taken in the city of New York over one year. The real-time implementation of the method with near-optimal service levels allow a 30 per cent reduction in fleet size compared to current taxi operation.Although constraints on driver availability and existence of abnormal trip demands may lead to a relatively larger optimal value for the fleet size than that predicted here,the fleet size remains robust for a wide range of variations in historical trip demand.These predicted reductions in fleet size follow directly from a reorganization of taxi dispatching that could be implemented with a simple urban app; they do not assume ride sharing, nor require changes to regulations,business models,or human attitudes towards mobility to become effective. Our results could become even more relevant in the years ahead as fleets of networked,self-driving cars become commonplace.
信息和通信技术为城市交通的新解决方案开辟了道路,为人们提供了更好的方式来与按需车辆相匹配。然而一个仍未解决的基本问题是如何在考虑个人的出行需求的情况下,最好地扩大和运营一支车队。之前的研究要么没有提供可靠的解决方案要么要求人们改变对出行的态度。这里我们提出一个基于网络的‘最小车队’解决方案,给定出行的集合(由原点、目的地和起始时间指定),如何在不引入延迟的情况下,决定能够服务所有要出行的乘客的最小的车辆数量。通过引入‘车辆共享网络’,我们提供了这个问题的最优计算效率解决方案,以及一个可用于实时实现的最优解决方案。我们在New York市一年内 的1亿5千万出租车出行数据集上测试所有的解决方案。该方法的实时实现,其服务水平接近最佳,与当前的出租车运营相比,其车队规模减少了30%。尽管对驾驶员可用性的限制和不常见的旅行需求的存在,可能会导致比这里预测的更大的机队规模的最佳价值,但在历史出行需求的不同变化中,车队规模仍然很大。这不需要假设共享出行,不要去改变规则,商业模式,或者人们对出行的态度来变的更有效率。我们的成果在未来几年在网络化的车队中会更加收到重视,当无人驾驶汽车更加司空见惯。
Two trends—the rise of the autonomous and connected car, and the emergence of a ‘sharing economy’ of transportation-seem poised to revolutionize the way personal mobility needs will be addressed in cities. The way current modes of transportation such as the private car, taxi or bus operate will be challenged and increasingly replaced by personalized, on-demand mobility systems operated by vehicle fleets, similar to what companies like Uber and Lyft offer. If such trends continue, they could lead to the displacement, or eventual disappearance, of jobs for bus and taxi drivers. Along with these possible societal costs, the transportation revolution could also offer immense benefits, including opportunities to resolve existing inefficiencies in individual urban mobility, thereby reducing traffic,whose carbon footprint currently accounts for about 23% of global greenhouse gas emissions.
两种趋势——自主和联网汽车的兴起,以及交通运输的“共享经济”的出现,似乎将彻底改变城市的个人出行需求。目前的交通方式,如私家车、出租车或公共汽车,将受到挑战,并越来越多地由汽车车队运营的个性化的按需出行系统取代,类似于Uber和Lyft这样的公司提供的服务。如果这种趋势继续下去,可能会导致公交车和出租车司机的失业或最终消失。除了这些可能的社会成本之外,交通运输革命还可能带来巨大的好处,包括解决城市交通中现有的低效率的机会,从而减少交通,其碳足迹目前约占全球温室气体排放量的23%。
To turn these opportunities into tangible environmental and societal benefits,autonomous and on-demand mobility systems need to be designed and optimized for efficiency, and integrated with carbon-efficient public transport. This requires the definition of models and algorithms for the evaluation of shared mobility systems that are both computationally efficient and accurate. The former property is mandated by the need to cope with hundreds of thousands (or sometimes millions) of trips routinely occurring in a large city. The latter property determines the relevance of the model results to the real world.
为了将这些机会转化为有形的环境和社会效益,需要设计和优化自主和按需移动系统,以提高效率,并与低碳高效的公共交通相结合。这就需要定义模型和算法来评估共享的移动系统的计算效率和准确性。前一种属性的是因为,系统需要处理成千上万(有时甚至是数百万)的出行,这些出行经常发生在一个大城市。后一种属性决定了模型结果与现实世界的相关性。
In what follows, we solve the ‘minimum fleet problem’ for the general case of on-demand mobility, and show that is solution for a specific case-taxi trips-could lead to breakthroughs in operational efficiency. To the best of our knowledge, no publicly available solution currently exists to address this minimum fleet-size problem at the urban scale for on-demand mobility in both private and public sectors. On the one hand, accurate methods based on mathematical programming (as traditionally used in the design of transportation systems) can handle only a few thousand trips or vehicles at most, which is well below the hundreds of thousands or even millions of trips or vehicles routinely operating in large cities. On the other hand, city-scale studies are obtained using a model of transportation based on aggregated mobility data and Euclidean spatial assumptions, and hence lack the resolution necessary to estimate the urban-scale benefits of vehicle sharing accurately.
在下文中,我们对于一般情况下按需出行的情况,解决‘最小车队问题’,并显示这种针对出租车出行的方案可能会在运营效率上取得突破。据我们所知,目前还没有公开可用的解决方案来解决这个在城市规模的最小车队问题,即私人和公共部门的按需出行。一方面,基于数学编程的精确方法(就像在传统应用在运输系统设计上的)最多只能处理几千次旅行或车辆,这远远低于在大城市日常运营的数十万甚至数百万的出行或车辆。另一方面,城市规模的研究基于聚合移动数据和欧几里得空间假设的交通模型,因此缺乏准确估计车辆共享的城市规模效益的必要解决方案。
We start form the notion of the shareability network introduced in ref.7, which did not focus on the dispatching of vehicles. The type of shareability network introduced here is profoundly different from the type studied previously: it models the sharing of vehicles, whereas previous networks modeled the sharing of rides.The main methodological contribution of this Letter is to show how this vehicle-sharing network can be translated into an exact formulation of the minimum fleet problem as a minimum path cover problem on directed graphs,thus establishing a connection to the rich applied mathematics and computer science field of graph algorithms. Besides revealing a structural property of computationally efficient algorithms for optimal vehicle deployment and dispatching. Although optimally solving the minimum fleet requires offline knowledge of daily mobility demand, in the following we also present a near-optimal,online version of the algorithm that can be executed in real time knowing only a small amount of the trip demand.
我们从不聚焦于车辆分配的‘可共享的网络’的介绍开始,
这里介绍的可共享的网络与之前的几种研究是截然不同的:**它模拟车辆的共享,而以前的网络则模拟出行的共享。这篇文章的主要贡献是展示如何将这个车辆共享网络转化为最小车队问题的形式,有向图的最小路径覆盖问题,从而建立的丰富应用数学和计算机科学领域的图形算法的连接。**除了揭示了计算效率算法的结构特性,以实现最优的车辆部署和调度。尽管最优解决最小舰队需要离线的日常出行数据,但在下面我们也提供了一个近乎最优的在线版本算法,可以实时执行,只知道少量的出行需求。
We are given a collection T of individual trips representing a portion of urban mobility demand during a certain time interval, such as a day. Each tip Ti ∈ T is defined as a tuple ( t i p , t i d , l i p , l i d ) (t^p_i,t^d_i,l^p_i,l^d_i) (tip,tid,lip,lid), where t i p t^p_i tip represents the desired pick-up time, l i p l^p_i lip the pick-up location, t i d t^d_i tid the drop-off time, and l i d l^d_i lid the drop-off location. Here, the pick-up time means the earliest time t i p t^p_i tip at which passenger can be picked up at location l i p l^p_i lip. The drop-off time means the estimated time of dropping off the passenger, calculated using a travel-time estimation model and assuming the passenger leaves the pick-up location at time t i p t^p_i tip. IN contrast to ref.17, travel times here are computed using the actual road network, and using global positioning system (GPS)-based estimations derived from the taxi trip dataset that account for hourly variations in traffic, as in ref.7. If the set T is extracted from a real-world dataset (for example, taxi trips), the times t i p t^p_i tip and t i d t^d_i tid represent the actual times at which a passenger is picked up and dropped off,respectively.
我们得到了一个个人出行的集合T代表一定时间间隔内的城市交通需求的一部分,比如一天之内。每一个出行Ti属于T被定影成一个元组 ( t i p , t i d , l i p , l i d ) (t^p_i,t^d_i,l^p_i,l^d_i) (tip,tid,lip,lid),,其中 t i p t^p_i tip 表示接到乘客的时间 l i p l^p_i lip是接乘客的地点, t i d t^d_i tid是乘客下车时间, and l i d l^d_i lid 是下车地点. 这里, 接乘客的时间t t i p t^p_i tip 表示乘客在上车点 l i p l^p_i lip能被接到的最早时间.下车时间表示计算的下车时间,通过一个计算模型计算,假设乘客在 t i p t^p_i tip离开上车点. ref.17相比, 这里的旅行时间是用实际的道路网络计算的,并使用全球定位系统(GPS)基于出租车旅行数据集的估计,这些数据记录了每小时的流量变化,如果从真实世界的数据集(例如,出租车出行)中提取出集合 T,那么时间 T i p T^p_i Tip和 T i d T^d_i Tid代表了一个乘客上车和下车的实际时间。
The minimum fleet problem is formally defined as follows:'find the minimum number of vehicles needed to serve all trips in T, given that a vehicle is available at each l i p l^p_i lip on or before t i p t^p_i tip'. A service designed around this problem is ideal from a passenger’s perspective,since a vehicle is guaranteed to be available at the desired location and time, On the other hand, the above problem formulation might entail substantial inefficiencies for the operator and the environment. Consider two consecutive trips T A T_A TA and T B T_B TB served by a single vehicle, and call the time needed to connect them the (trip) connection time, formally t A B = t B p − t A d t_{AB} = t^p_B -t^d_A tAB=tBp−tAd. If this time is very long, say, a few hours, it is trivially possible to connect trips that occur at distant location or times. Hence, an excessively large connection time leads to inefficiencies for the operator (longer traveled distances,lower vehicle occupancy ratio) and the citizens (a lot of emissions and traffic just to connect trips). we therefore re-formulate the problem as follows:‘find the minimum number of vehicles needed to serve all trip in T,under the assumptions that (1) a vehicles is available at each l i p l^p_i lip on or before t i p t^p_i tip and (2) the connection time is at most δ \delta δ minutes’, where the upper bound δ \delta δ on the connection time is a problem parameter.
最小车队问题的正式定义如下:‘找到最小所需的车辆来服务所有集合T中的出行,给出一辆在时间 t i p t^p_i tip 之前,在 l i p l^p_i lip可用的车’。以此定义的服务是完全从乘客的角度来看的,因为一辆车保证能在预定的时间和地点使用。另一方面,上述问题的制定可能会导致操作人员和环境的效率低下。考虑两个出行 T A T_A TA和 T B T_B TB 被同一辆车服务,把连接他们的时间成为连接时间,正式的, t A B = t B p − t A d t_{AB} = t^p_B -t^d_A tAB=tBp−tAd。如果这个时间很长,假如,几个小时,在很远的地方或较长的时间上连接出行也是可能的。因此,过多的连接时间会导致操作员(长途旅行距离,车辆占用率较低)和市民(大量的排放和交通只是为了连接旅行)的效率低下。因此,我们将如下问题重新表述如下:‘找到最小所需的车辆来服务所有集合T中的出行,并满足(1)车辆在时间 t i p t^p_i tip 之前,在 l i p l^p_i lip可用 (2)连接时间最大不超过 δ \delta δ 分钟’,连接时间中的上限 δ \delta δ是问题的一个从参数。
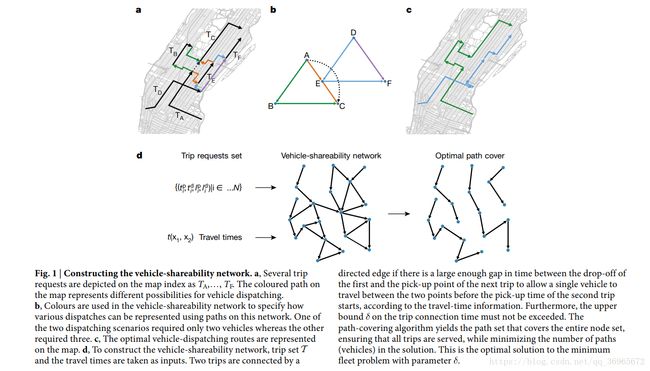
figure 1 illustrates the construction of the vehicle-shareability network that enables the minimum fleet problem to be optimally solved with parameter δ \delta δ . This is a directed network defined as V = (N,E), where node n i n_i ni ∈ \in ∈ N corresponds to trip Ti ∈ \in ∈ T and the directed edge ( n i n_i ni, n j n_j nj) ∈ \in ∈E if and only if ( t i d + t i j ) ≤ t j p t^d_i +t_{ij} ) \le t^p_j tid+tij)≤tjp (which accounts for assumption (1) above) and t j p − t i d ≤ δ t^p_j -t^d_i \le \delta tjp−tid≤δ (which accounts for assumption (2) above). Here t i j t_{ij} tij represents the estimated travel time between l i d l^d_i lid and l j p l^p_j ljp. The existence of a link in the network indicates that the two incident trips can be consecutively served by a single vehicle, and a path in V corresponds to a sequence of trips that can be served by a single vehicle- that is, a dispatch. There for, solving the minimum fleet problem is equivalent to finding the number of paths(vehicles) in the minimum path cover of V. The solution also gives the optimal dispatching strategy, that is, a sequence of trips to be served for each vehicle in the minimum fleet. The problem of finding the minimum path cover on general graphs is NP-hard, but it can be solved efficiently on directed acyclic graphs 19 ^{19} 19. The acyclic nature of time guarantees that any vehicle shareability network is a directed acyclic graph, and the minimum fleet problem can be efficiently and optimally solved; see Methods for formal proofs
图1描述了能够解决带参数 δ \delta δ的最小车队问题最优解决的车辆共享网络的结构,这个有向网络的定义是 V=(N,E),其中节点 n i ∈ n_i \in ni∈ N 相当于 出行记录 Ti ∈ \in ∈ T 并且 有向边( n i , n j ) ∈ n_i,n_j) \in ni,nj)∈E 当且仅当( t i d + t i j ) ≤ t j p t^d_i +t_{ij} ) \le t^p_j tid+tij)≤tjp (依据假设(1)) ,并且 t j p − t i d ≤ δ t^p_j -t^d_i \le \delta tjp−tid≤δ (依据假设(2))。这里, t i j t_{ij} tij 代表计算出来的从 l i d l^d_i lid 到 l j p l^p_j ljp的行驶时间。网络中存在的一个连接表明两个不同的出行可以被同一辆车连续的服务,V 中的路径相当于一辆车行驶的顺序,这就是分配。这样,解决最小车队问题和找到覆盖V的最小的路径条数是等价的。这个解决方案还提供了最优调度策略,也就是说,在最小车队中,每辆车都要进行一系列的行驶。在一般图上找到最小路径覆盖的问题是NP-hard,但是它可以在有向无环图中有效地解决,通过使用 Hopcroft-Karp算法计算二分图匹配。时间的无环特性保证了任何车辆的可共享网络都是一个有向无环图,最小车队问题可以得到有效和最优的解决;正式的证明看Methods。
We have tested our methodology on a dataset of over 150 million trips performed in the city of New York in the year 2011. This dataset has been selected form a number of available datasets because it is publicly available and, thanks to taxi statistics published by the New York Taxi and Limousine Commission 6 ^6 6, it is possible to compare our methodology directly with current taxi operation. The data have been sliced into daily datasets Ti, each of which is an input to the minimum fleet size problem.
我们在2011年纽约城市进行的超过1.5亿次的出行数据上测试了我们的方法。这一数据集从为许多可用的数据集被选出,是因为它是公开可用的,而且,由于纽约出租车和豪华轿车委员会发布的出租车统计数据,我们可以直接将我们的方法与当前的出租车运营进行比较。这些数据按天数来进行分割,每一个都是对最小车队大小问题的输入。
Next,we discuss how to set the parameter δ \delta δ. When δ \delta δ is decreased to 0, we approach a situation in which each trip is served by a dedicated vehicle: a solution with maximal vehicle utilization that is also optimal for traffic- under the assumption that vehicles materialize at the origin and dematerialize at the destination of the served trip- but incurring prohibitive cost for the mobility operator. On the other hand, when δ \delta δ grows excessively, the fleet size is reduced, but the operational and traffic efficiency problems described previously occur. Thus, the setting of δ \delta δ is an important design choice that is left to mobility operators,traffic authorities and policy makers. In this study, we set δ \delta δ = 15 min, as explained in Methods. The results of our method with different values of δ \delta δ are reported in Methods (see Extended Data Fig.1)
接下来,我们将讨论如何设置参数 δ \delta δ。 δ \delta δ下降到0时,我们的方法中,每个出行是由一个专门的车辆负责:一个解决方案与最大车辆利用率也适合交通——假设下车辆出现在原点,消失在目的地的旅行,但移动运营商承担高昂的成本。另一方面,当 δ \delta δ过度增长时,车队的大小会减少,但是前面描述的操作和交通效率问题出现了。因此, δ \delta δ的设置是一个重要的设计选择,留给移动运营商、交通部门和政策制定者。在这项研究中,我们设置了 δ \delta δ=15分钟,正如在方法中所解释的那样。我们的方法在不同的 δ \delta δ值下的结果在Methods中被报告(见Extended Data Fig.1)
Figure 2 shows the daily number of vehicles needed to address the entire taxi demand in New York City using our approach.The minimum number of vehicles needed to serve trips is correlated with the number of daily trips (see Fig. 2a), with an overall R 2 ^2 2 value of 0.74.However,for the vast majority of days having between 300,000 and 550,000 trips (inset to Fig. 2a) this correlation becomes much weaker, with an R 2 ^2 2 value of only 0.18. Thus,trip density is a first determinant of fleet size, but trip spatiotemporal patterns are likely to play a large part as well. To investigate this issue further, we have analysed daily vehicle usage in the optimal solution。
图2显示了每天所需的车辆数量来满足纽约市所有的出租车需求。所需要的最少车辆数量与每天的出行需求相关(见图2a),总体的R 2 ^2 2 值为0.74。然而, 在绝大多数的天数中,有300,000到550,000的出行需求,这种相关性就变得更弱了,R 2 ^2 2的值只有0.18。这样,因此,行程密度是车队规模的第一个决定因素,但出行的时空模式也可能发挥很大的作用。为了进一步研究这个问题,我们分析了最优解的日常车辆使用情况。
The vehicle usage analysis reported in Method shows that a fraction of vehicles, ranging between 5% and 10%, are highly underutilized and serve only around 1% of the trips, a lower utilization pattern that occurs especially during the weekend and is probably related to the extra nightly demand. The analysis also highlight clear weekly patterns in vehicle use, consistent with the relatively stable vehicle fleet size across the year.This observed stability can be explained by a simple model for vehicle trip assignment, and is fundamental for mobility operators: it indicates that investment in acquiring an optimal number of vehicles for operation gives consistent yearly returns. The dip in vehicle fleet size occurring at weekends hints also at an opportunity to perform routine vehicle maintenance on a weekly basis.
在Methods中报告的车辆使用分析显示,一小部分车辆,在5%到10%之间,的利用率非常低,只提供了大约1%的行程,较低的利用率经常是在周末发生,可能与夜间额外需求有关。该分析还强调了汽车使用的每周模式,这与全年相对稳定的车队规模一致。这种观察到的稳定性可以用一个简单的车辆旅行分配模型来解释,这对于移动运营商来说是最基本的:它表明,在获得最佳的运营车辆的投资上,每年的回报是一致的。周末发生的车辆数量下降也暗示了每周例行的车辆维修的机会。
A better scaling law relating vehicle fleet size to the daily number of trips can be obtained by defining a metric for fleet sizing that incorporates how long a vehicle is used during a day. We define a ‘full-time equivalent’ vehicles as a vehicle continuously operating 24h a day.(In this case of human-driven vehicles, we can think of having the vehicle operated in three 8-h shifts,for instance.) Figure 2b shows that the scaling law relating the number of daily trips with full-time equivalent vehicles is more accurate than the previous one, with the coefficient of determination R 2 ^2 2 value increased from 0.74 to 0.91, and from 0.18 to 0.70 for trip-intense days reported in the inset.
一个更好的关于车队大小和每天出行次数的标度律可以通过定义一个车队大小的标准来获得,其包含每天使用的车辆的时间相结合。我们定义了一种“全天等效”的车辆,作为一种连续运行24小时的汽车。(在这种情况下,我们可以考虑让汽车在3个8小时的轮班中运行)图2b显示,与前一辆车的每日出行次数有关的标度律比前一项更准确,其确定系数为R 2 ^2 2,从0.74增加到0.91,在出行紧张的日子里为为0.18至0.70,见图。
Figure 3 shows the efficiency breakthrough provided by network-based optimization: when compared to current taxi operation in New York City, the number of circulating taxis can be reduced by an impressive 40%, and kept fairly constant through the day. This improvement is all the more noticeable considering that it is achieved without imposing any delay on customers, nor sharing of rides as in refs. 7.9 ^{7.9} 7.9. That fleet size can be reduced by as much as 40% without the use of ride sharing and with on delay for passengers has, to the best of our knowledge, not been reported in the literature before, and it is one of the main results of this paper.
图3 显示了基于网络的优化在效率上的突破:与当前纽约市的出租车调度相比,路上巡弋的出租车可以检查惊人的40%,并且保持平时的出行条件。考虑到这一改进是在不延误客户的情况下实现的,也不像在refs 7 , 9 ^{7,9} 7,9中共享乘车服务那样,这种改进更加引人注目。在不使用拼车服务的情况下,车队规模可以减少40%,而对于乘客来说,在我们的知识中,这是我们所知的最好的情况,这是本文的主要成果之一。
The 40% fleet reduction reported above refers to the model with full knowledge of daily trip demand. If only a portion of trip demand is known, as in current on-demand mobility services where trip requests are collected in real time, we can still achieve near-optimal performance with the online version of the algorithm reported in the Methods. This version collects trip requests for a short time ,for example, one minute, and locally optimizes vehicle dispatching based on this limited knowledge.Figure 4 shows that, with a 30% fleet reduction and using the online version of the algorithm, more than 90% of the trip requests can be successfully served. hitting a performance very close to the 40% fleet reduction possible when the entire daily demand is known beforehand,
上面报告的40%的车队减少是指对每日出行需求有充分了解的模型。如果只知道出行需求的一部分,就像当前按需出行服务那样,在实时收集旅行请求的情况下,我们仍然可以通过在方法中报告的算法的在线版本实现近乎最佳的性能。这个版本在短时间内收集旅行请求,例如,一分钟,根据有限的知识在本地优化车辆调度。图4显示,使用了该算法的在线版本,减少了30%的车队。如果超过90%的出行请求可以被成功的服务。当所有的日常出行请求都事先知道的时候,就能达到接近40%的车队减少的效果,
Our approach assumes that trip requests and vehicle-dispatching decisions are centralized, a model that is radically different from current taxi operation and similar to the one used by online mobility operators. Therefor, the benefits of optimized operation from a fully distributed operation, where the deployment strategy is based on individual driver decisions, to a centralized operation, where dispatching decisions are globally optimized. To some extent, our results can then be seen as a quantification of the well known game-theory notion of the ‘price of anarchy’ 20 ^{20} 20 in urban taxi operation. Taking a mobility market perspective, this is a transition from a regulated mobility market with numerous micro-operators (down to the level of the single taxi driver), to a monopolistic market with a single mobility operator with centralized operation. Although optimal from the vehicle operation and environment viewpoint, a monopolistic market is however highly undesirable for many other reasons, most importantly, lack of competition with consequent higher prices for customers. An additional analysis reported in Methods shows that most of the efficiency benefits of centralized vehicle operation are still possible in an oligopolistic market.
我们的方法假定旅行请求和车辆调度决策是集中的,这一模型与当前的出租车操作完全不同,类似于在线移动运营商使用的模式。因此,从完全分布的操作中优化操作的好处,即部署策略基于单个驱动程序决策,到一个集中的操作,在那里调度决策是全局优化的。在某种程度上,我们的研究结果可以被看作是对“无政府主义价格”的一个众所周知的博弈论概念的量化,即“无政府主义的价格”在城市出租车运营中所占的20美元。从流动市场的角度来看,这是一个由监管的流动市场与众多微型运营商(降至单一出租车司机的水平)的过渡,到一个垄断市场,一个单一的移动运营商集中运营。尽管从汽车运营和环境观点来看,垄断市场是最不受欢迎的,但由于许多其他原因,最重要的是,缺乏竞争,从而导致更高的价格。在方法中报告的另一项分析表明,在一个寡头垄断的市场中,集中的车辆操作的大部分效率效益仍然是可能的。
Although the characterization of minimum fleet size reported here is fully representative of an autonomous driving scenario where human operation of vehicles is not necessary, constraints on driver availability and maximum operating hours, shift operation and so on might produce relatively larger values of the minimum fleet requirement than those predicted here. Extending the concept of the vehicle -sharing network to incorporate driver constraints is possible and is left for further analysis.
Boarder effects on traffic are foreseen if our methodology is to be used for optimizing urban ‘on-demand’ mobility services more in general, especially in a future of autonomous vehicles. However, it is well know that an improvement in mobility efficiency is sometimes linked with an increase in demand which, in turn, could reduce the amount of traffic reductions. Evaluating this ‘second-order’ effect of optimized fleet operation on urban traffic requires coupling a micro-level traffic simulation, agent-based passenger models and our network-based methodology, a challenging task which wee leave to future work.
Finally, we observe that, while applied here to taxi trips as a case study, the proposed methodology for optimal vehicle fleet sizing and dispatching is general and can be applied to model any type of point-point mobility. However, the approach presented here focuses on optimizing and dispatching a single fleet of vehicles. Optimization across different fleets and transportation modes is possible by extending our approach to consider multiple coexisting fleets of various types to serve the mobility demand. With the approaching advent of autonomous mobility and the forecast increase in sharing cars (or other autonomous vehicles, such as flying drones), the problem of how to optimize and orchestrate multiple autonomous fleets will come to the forefront, and might be addressed using the scalable and accurate analytical tools presented here for optimal solution of the ‘minimum fleet’ problem.
METHODS
**Trip data.**The dataset used in this work consists of more than 150 million trips with passengers of all 13,586 taxicabs in New York City during the calendar year of 2011. The dataset contains a number of fields from which we use the following: origin time, origin longitude, origin latitude, destination longitude and destination latitude. The measurement precision of times is in seconds: location information has been collected by the data provider via GPS location tracking technology. Out of our control area possible biases due to urban canyons (that is, streets with high-rise building on both sides), which might have slightly distorted the GPS locations during the collection process. All individual-level identifications are given in anonymized form; origin and destination values refer to the origins and destinations of trips, respectively.
Map matching. Similar to the preprocessing done in ref. 7 ^7 7, we used data from www.openstreetmap.org to create the street network of Manhattan. As described in previous work 7 ^7 7, we used a filtering method on the streets of Manhattan to select only the following road classes: primary, secondary,tertiary, residential, unclassified, road and living street. We left out several other classes deliberate. These include footpaths, trunks,links or service roads, as they are unlikely to contain delivery or pick-up locations. We extracted the street intersections to build a network in which nodes are intersections and directed links are roads connecting those intersections (we use directed links because a non-negligible fraction of streets in Manhattan are one-way). The extracted network of street intersections was then manually cleaned for obvious inconsistencies or redundancies (such as duplicate intersection points at the same geographic positions), in the end containing 4,091 nodes and 9,452 directed links. This network was used to map match the GPS locations from the trip dataset. We matched only GPS locations (both trip origins and destinations) that are within 100m of at least one node in the street intersection network, which is the case for the majority of trips, and discarded the remaining ones. After the preprocessing and filtering phase, more than 147 million trips remain to be used in the next phases of our analysis.
**Travel-time computation.**Travel-time information is a key part of building vehicle-shareability network. The knowledge of estimated travel times is based on a heuristic method developed and used in ref. 7 ^7 7. This method uses pick-up and drop-off times of a historical trip dataset and computes the travel times between arbitrary origins and destinations on the road map.
In the following we briefly describe the core idea of this method. A detailed description can be found in the supplementary information of ref. 7 ^7 7.
Each street segment belongs to the set, S={S 1 _1 1,…,S h _h h}, of all road segments connecting any pair of adjacent intersections in the road map. Given a set of k historical trips T={ T 1 , . . . , T k T_1,...,T_k T1,...,Tk}, the problem of travel-time computation is estimating the travel time t i e t^e_i tie for each street segment S i ∈ S S_i \in S Si∈S in such a way that the average relative error (computed across all trips) between the actual travel time t i t_i ti and the estimated travel time t i e t^e_i tie for trip T i T_i Ti computed starting from the x i x_i xi (compound with a routeing algorithm) is minimized. Once error-minimizing travel times for each street in S are determined, the travel time between any two intersections i and j can be computed staring from the t i t_i ti values, using a routeing algorithm that minimizes the travel time between any intersections.
The following steps are involved in the process of travel-time computation. First, we partition the trip set in time-sliced subsets T 1 , . . . , T 24 T_1,...,T_{24} T1,...,T24 where subset T i T_i Ti contains all trips whose starting time is in hour i of the day. IF desired, finer partitioning (for example, per hour and weekday, per hour and weekday and month, and so on) is possible. he travel-time estimation process can be performed independently on each of the time-sliced trip subsets. We defined T i s q T^{sq}_i Tisq as the subset of trips with origin x s x_s xs and destination x q x_q xq in which x s x_s xs contains the (latitude, longitude) coordinates of the sth intersection after the trips are matched. A small fraction of trips are filtered to remove ‘loop’ trips (that is, trips with the same origin and destination), as well as excessively short or long trips. After a step in which initial route are computed using a pre-selected initial speed v i n t v_{int} vint (the same for all streets) as described in ref. 7 ^7 7., a second trip-filtering step is performed, in which excessively fast and slow trips are removed from the travel-time estimations. 97% of trips remain after this filtering. The travel-time estimations obtained using this method are reasonable, with a relatively lower average speed of around 5.5ms − 1 ^{-1} −1 estimated during rush hours (between 8 am and 3 pm), and peaks at around 8.5 m s − 1 8.5ms^{-1} 8.5ms−1 at midnight.
Node-disjoint path cover. In the following we provide a set of definitions and present relevant theorems with their proofs to systematically formulate the problem of reducing the fleet size as path-covering problem on a vehicle-shareability network.
Given a directed network V= (N,E), a path P in V is a sequence of edges e 1 = ( n 1 1 , n 1 2 ) , . . . , e k = ( n k 1 , n k 2 ) ∈ E {e_1=(n^1_1,n^2_1),...,e_k=(n^1_k,n^2_k)} \in E e1=(n11,n12),...,ek=(nk1,nk2)∈E such that n i 2 = n i + 1 1 n_i^2 = n^1_{i+1} ni2=ni+11, for each i=1,…,k-1. The set of nodes in path P is defined as N§ = ∪ i = 1 , k n i 1 \cup_{i=1,k} {n^1_i} ∪i=1,kni1. The length of a path P is the number of edges k that form it.
Definition 1(Path cover). Given a directed network V=(N,E), a node-disjoint path cover of V is a collection of paths P 1 , . . . , P h {P_1,...,P_h} P1,...,Ph such that ∪ i = 1 , h N ( p i ) \cup_{i=1,h} N(p_i) ∪i=1,hN(pi) =N and N ( P i ) ∩ N ( P j ) = ∅ N(P_i) \cap N(P_j) = \empty N(Pi)∩N(Pj)=∅ for any i ≠ \ne ̸= j. The size of the cover is the number of paths h of which it is formed,
We note that, under the conventional assumption that zero-disjoint path cover always exists. In the following, to simplify presentation we drop the term ‘node-disjoint’ and use ‘path cover’ to refer to a ‘node-disjoint path cover’ as defined in ‘Definition 1(Path cover)’ above.
*Theorem 1. * Let C=%{P_1,…,P_h}% be a path cover of the vehicle-shareability network V=(N,E). Then, all the trips in T can be served by h vehicles.
*Proof.*Consider a path P={ e 1 = ( n 1 1 , n 1 2 ) , . . . , e k = ( n k 1 , n k 2 ) e_1 = (n^1_1,n^2_1), ..., e_k =(n^1_k,n^2_k) e1=(n11,n12),...,ek=(nk1,nk2)} in the vehicle-shareability network V. By definition of shareability network, the trips corresponding to n 1 1 n^1_1 n11 and n 1 2 n^2_1 n12(call them T 1 a n d T 2 T_1 and T_2 T1andT2) can be served by a single vehicle, Furthermore, the vehicle performing trip T 1 T_1 T1 is guaranteed to arrive at the pick-up location of T 2 T_2 T2 with time t 2 p t^p_2 t2p; that is, vehicle sharing does not impose any delay on the starting time of the second trip. Also, the upper bound δ \delta δ on the trip connection time is not violated by the definition of shareability network. Hence, the vehicle that serves T 1 a n d T 2 T_1 and T_2 T1andT2 can be used to serve trip T e T_e Te corresponding to node n 2 2 n^2_2 n22 in V, since the starting time of trip T 2 T_2 T2 is not changed as a result of sharing, implying that the condition ensuring shareability of T 3 T_3 T3 and T 2 T_2 T2 is still fulfilled. By iterating the argument across all nodes in N§, we can conclude that all trips whose corresponding nodes are in N§ can be served by a single vehicle. Thus, if a path cover of size h exists, we can conclude that all trips in T can be served by h vehicles.
Corollary 1 The minimum number of vehicles needed to serve the trips in T equals the size of the minimum path cover of the vehicle shareability network V= (N,E).
Finding the size of the minimum path cover of an arbitrary directed network is NP-hard 1 8 ^18 18 and hence computationally infeasible for large graphs. However, the optimal solution can be found in polynomial time if the network is acyclic, meaning that there is no directed path in the network forming a closed loop.
Definition 2 (Directed acyclic network). A directed network V(N,E) is acyclic if it has no directed cycles, that is, it does not contains directed paths starting at some vertex n ∈ \in ∈ N and eventually returning to n again.
Any vehicle-shareability network as defined above is a directed acyclic network. To see how the acyclic character arises one can use proof by contradiction. Assume a cyclic path exists in V. For simplicity, assume the path has minimal length of 2. Let P= ( n 1 , n 2 ) , ( n 2 , n 1 ) {(n_1,n_2),(n_2,n_1)} (n1,n2),(n2,n1) be a cyclic path, and let T 1 T_1 T1 and T 2 T_2 T2 be the trips corresponding to n 1 n_1 n1 and n 2 n_2 n2, respectively. By the definition of vehicle-shareability network, we have the following sequence of inequalities:
t 1 d ≤ t 1 d + t 12 ≤ t 2 p ≤ t 2 d ≤ t @ d + t 21 ≤ t 1 p t^d_1 \le t^d_1 +t_{12} \le t^p_2 \le t^d_2 \le t^d_@ + t_{21} \le t^p_1 t1d≤t1d+t12≤t2p≤t2d≤t@d+t21≤t1p
which is a contradiction since t 1 d > t 1 p t^d_1 > t^p_1 t1d>t1p. Hence, no cyclic path of length 2 can exist in V. The proof follows by straightforwardly extending the above sequence of inequalities to cyclic paths of arbitrary length. This implies that the minimum number of vehicles needed to perform a set T of trips can be computed in polynomial time. More specifically, it is shown that for directed acyclic networks the problem of finding the path cover of minimum size is equivalent to the well known maximum matching problem on bipartite graphs, which can be solved in time O(|E|(|N|) 1 / 2 ^{1/2} 1/2) using the Hopcroft-Karp algorithm.
Online model. The results shown so far compute the minimum infrastructure on the basis of the knowledge of the entire shareability network for the day considered. This is analogous to the Oracle model as defined in ref. 7 ^7 7, and is consistent with a scenario in which trip requests are issued in advance (for example, through a reservation system). To investigate to what extent the above described benefits extend to systems where trip requests are issued in real time (such as Uber and Lyfy), we repeat the analysis in the so-called online model. In the online model, we have a number of vehicles available for serving trips, which is defined as N=N m i n x _{min}x minx, where N m i n x _{min}x minx is the minimum fleet size for the day of reference as computed by the oracle model, and x>1 is an inflating factor. We then start serving trip requests with the available vehicles, whose initial position is determined through a warm-up phase in which a number of trip requests form the previous day (not accounted to compute the results) are served. To compare online models, two possible strategies are used to dispatch vehicles and serve trip requests, as follows.
On-the-fly. Trip requests are served sequentially; when a new trip request is issued, the dispatched vehicle is chosen as the first available vehicle that minimizes passenger waiting time.
*Batch.*Trip requests are collected for time δ \delta δ = 1 min and processed in batches. When a batch is processed, a maximum matching is computed to maximize the number of requests that can be successfully served (that is, served within max( Δ t \Delta t Δt)= 6 min); vehicles area then dispatched on the basis of the result of the maximum matching algorithm, as explained in the following. At each given minute the trip requests information and the locations of the available vehicles are compiled to construct a weighted bipartite graph. The edge weight on a pair of vehicle-trip node represents the pick-up delay a passenger associated with the trip node would experience in case the vehicle associate with the vehicle node is chosen to serve the passenger. After constructing this weighted bipartite network, the maximum matching algorithm can be used to find a subset of edges covering the maximum number of trip nodes served with the tolerable delay,max( Δ t \Delta t Δt).
Figure 4 shows the success rate of the two dispatching algorithms for a period of 15 consecutive days. for x= 1.2, serving the trips within a certain tolerable delay. As seen in this figure , the batch method(blue lines) provides a success rate which is consistently above 92%,and is much higher than what is achieved by the sequential on-the-fly method for max( Δ t \Delta t Δt) = 6 min. As reported in Extended Data Table 1, the running times of the online version of the method are below 200ms in the worst-case scenarios on a standard Linux machine, indicating the feasibility of the proposed approach for real-time optimization.
The warm-up phase used in the above-mentioned online optimizations consists of first deploying each vehicle at a random intersection, then running the batch optimization algorithm as described above on the 2h of historical trip requests that precede the period of interest. The shaded regions in Fig.4a and c and in Extended Data Fig.3 represent the variation in the percentage of the trip served as obtained by running the real-time optimization for each day multiple times, each time reinitializing the warm-up phase with a distinct random initial deployment of the fleet. The variations are quite small, showing that within 2H the system’s spatiotemporal distribution does not depend noticeably on the initial deployment.
Limiting node connectivity via trip connection time. We defined the vehicle-shareability network in such a way that nodes that represent individual trips are connected only if it is feasible for a vehicle to serve those trips one after the other without introducing any delay in their pick-up and drop-off times. Checking whether two trips satisfy such criteria requires knowledge of travel times in the city, which is estimated using the method described previously. Since this network definition puts no constraints on the connectivity apart from the feasibility of consecutively serving trips, the number of network links grows quickly with the increase in the number of trips. This is because trips separated by a large enough time gap between their drop-off and pick-up times can always be served by the same vehicle although they may be spatially far from each other. This leads to a very high connectivity in the vehicle-shareability network because most pairs of trips separated by enough time can satisfy this connectivity condition. To limit the number of edges in the network, and to make sure that the vehicles do not operate without any passenger onboard for too long leading to underutilization and an increase in the void ratio (the fraction of time vehicles operate without a passenger), we introduce an upper bound on the connection time between the trips. The connection time is defined as the time a vehicle operates without a passenger between the consecutive trips.
The first issue to address is how to set the bound δ \delta δ on the trip connection time, which is a parameter that can be used to trade off fleet size against vehicle and traffic efficiency. On the one hand, when δ \delta δ is decreased to 0 we approach a situation in which each trip is served by a dedicated v
vehicle: a solution with maximum vehicle utilization that is also optimal for traffic (if we assume that vehicles somehow appear at the origin and disappear at the destination of the trip they serve), but incurring prohibitive costs for the mobility operator. On the other hand, when δ \delta δ grows excessively the fleet size is reduced, but this is at the expense of a decrease in the operational and traffic efficiency because some vehicles may be on the road for long times without any passenger on board between serving the trips. Thus, how to set δ \delta δ is an important design choice, which should be left in the hands of mobility operators, traffic authorities and policy makers.
Extended Data Fig.1 shows how we comp up with a reasonable setting for δ \delta δ. The plot reports both the minimum fleet size as well as the average fraction of time a vehicle spends connecting consecutive trips(the void ratio) in seconds, for increasing value of δ \delta δ. As expected, the former quantity decrease with δ \delta δ, while the latter increase. For value of δ \delta δ large that 15 min, however, the vehicle fleet size decreases only marginally, whereas the void ratio still increases. or reference, the right panel of Extended Data Fig.1 reports the yearly analysis of minimum fleet size-similar to what is reported in Extended Data Fig.2- for δ \delta δ =10 min and 20 min.
vehicle utilization. A better understanding of the efficiency of the network-based vehicle-trip assignment requires a closer look into the patterns of the utilization of the individual vehicles in the minimum fleet, The overall time each vehicle spends during its operation in a day consists of travelling with a passenger on board, without any passenger an d on the way to pick up the next one, or waiting at the pick-up location of a new passenger. Ultimately, the goal in an efficient vehicle-trip assignment is to maximize overall utilization while minimizing the operation costs. This is achieved for each vehicle when the fraction of time a vehicle operates without a pssenger on board is minimized.
Extended Data Fig,2 reports the yearly analysis of minimum fleet requirements, along with the corresponding daily number of trips. Whereas the number of daily trips clearly displays an increasing weekly pattern, the number of required vehicles remains fairly constant, with a dip on Sundays. The robustness of the fleet size despite large variation in the number of daily trips shows that the minimum fleet size can tolerate handling extra trips without needing extra vehicles. The addition of such trips certainly leads to higher vehicle utilization, as we show here. Extended Data Fig.4 reports a break down of the deployed vehicles into the different phases of deployment-passenger onboard, en route to next passenger, waiting for next passenger - for a better understanding of the utilization patterns.
Extended Data Fig.5 reports vehicle level performance using various temporal metrics. The vehicle start and end of operation time during the day in Extended Data Fig.5a shows that on most days, minimum fleet assignment leads to high operation times for the majority of the vehicles. The reported plots in Extended Data Fig.5b and c on some days clearly show the existence of a small fraction of under-used vehicles operating on average for less than two hours, serving what we call ‘special-purpose’ trips. These trips occur mostly on the weekend and are spatiotemporally isolated, meaning that their existence requires new vehicles because the existing vehicle-trip assignment cannot be rearranged to accommodate these trips successfully.
A bin-packing model to describe fleet-size scaling. As shown in Extended Data Fig.6, for a large number of days with daily trips ranging from 350,000 to 550,000, there is only a small variation in the minimum fleet size. This pattern seems a bit counter-intuitive at first glance, because basic logic implies that an increase in the number of trips should somehow lead to increase in fleet size. Outside this range this expected increasing pattern holds and for a smaller number of trips we have a more-or-less linear scaling (see the result of supersampling in Extended Data Fig.6c).
To explain the saturation pattern observed in Fig.2, we use a simple bin-packing model to show that the reason for fleet-size robustness within a certain range is related to an existing spatiotemporal capacity to accommodate more trips in the minimum fleet. Consider a set of N vehicles with a fixed spatiotemporal capacity to accommodate k trips during a given time of the day, and it is limited by an strict upper bound equal to 24 h on the maximum vehicle operation time. We start with a configuration where we have certain number of trips Nx(where x ≪ \ll ≪ k) randomly distributed in the bins with a Poisson distribution. We start to add one trip at a time and randomly sample a small subset of n vehicles as candidate set (n is a hyperparameter of the model that we assume to be either 1 or 2). Two scenarios are possible: (1) a subset of the selected vehicles still have the capacity to accommodate more trips, in which case we randomly select one of them and assign the tip tp that vehicle; (2) none of the vehicles have spatiotemporal capacity to accommodate the new trip, in which case we add a new vehicle to the system to accommodate the new trip. We repeat this process and model the relationship between the number of vehicles and number of trips in this manner.
An interesting plateau-then-increase pattern emerges from this model, which implies that for some intermediate ranges, the fleet size first increases and then shows some robustness with respect to a further increase in the number of trips, consistent with the observed pattern as observed from our minimum fleet optimization approach in Fig.2. This simple model suggests that the reason for the minimum fleet-size robustness is that the probability of finding a vehicle which can successfully accommodate that new trip is still relatively high as many cars operate with a large unused spatiotemporal capacity when the number of trips is relatively low. The range of minimum fleet-size tolerance is determined by the maximum number of trips that a certain number of vehicles can serve in theory. This maximum number depends on the spatiotemporal distribution of trips, especially the distribution of the trip durations. For instance, if the average trip duration in a day is 10-15 min, a vehicle can serve up to around 3-4 trips per hour assuming a 5-min connection time between the trips on average. In this way the upper bound would be around 100 trips for vehicles that are active for most of the day. With this assumption the maximum number of trips a minimum fleet of around 6.000 vehicles can tolerate is around 600,000 trips. Figure 2 and the results of the model in Extended Data Fig.6d support this argument.
Although the model in this section is an oversimplification and does not consider the complex spatiotemporal constraints that determine whether a vehicle can serve a trip, it does, however, capture the saturation pattern represented in Fig.2. Extended Data Fig.7 supports the idea that the robustness of the fleet size is due to the existing capacity in vehicles by showing how the metrics associated with vehicle utilization show a consistent increase in vehicle utilization for days with higher numbers of trips. Days with higher numbers of trips score higher average utilization per vehicle as can be seen in both the increase in the average time a vehicle spends on the road with a passenger on board for each day (see Extended Data Fig.7a) and also in the increase in the average time vehicles spend waiting to pick up a passenger at the pick-up point (see Extended dta Fig.7b).
Multi-operator model. As briefly discussed in the main text, consider a situation in which there is more than one mobility operator, each having access only to a subset of trip demand data and assuming that the operators assign the vehicles in their fleet to the trip demands they have access to without sharing information with the other mobility operators. The question is to what extent the fleet size is affected by the lack of information sharing between a certain number of mobility operators. This is equivalent to going from a global optimum to a local optimum in which each vehicle receives limited information about adjacent trips and tries to maximize its utilization independent of other vehicle. This latter situation is the extreme limit at which the number of operators is very large and only a local optimum can be achieved. In the following, using a simplified model we try to address the cases for two and three mobility operators equally sharing the mobility market.
For this purpose we randomly sample the trip demand data at each given point in time and divide the trip set into multiple subsets. For each trip subset we can build a vehicle-shareabililty network and do the minimum fleet optimization as described in the Letter. Each optimization leads to a minimum fleet size or each mobility operator. By comparing the sum of the fleet sizes for the multiple mobility operator case with the global minimum fleet size we can find out how far away we are from the global optimum.
Extended Data Fig.8 shows the temporal pattern of the sum of fleet sizes for a sample of 100 days from new York City taxi trip data. To obtain a good estimate for the sum of fleet sizes, we have divided the trip set in each day into two and three equally sized subset by random subsamplings. We repeated the random subsampling several times and each time we perform the vehicle-shareability network optimization to find the fleet size for each subset. The average fleet size obtained form several random subsampling each day is then presented in Extended Data Fig.8a and b. As shown in Extended Data Fig.8b, the transition from a monopolistic to a oligopolistic market incurs a small drop in efficiency quantifiable at about 4%-6$ for two-operator markets, and about 6%-10% for three-operator markets. A further increase in the number of operators leads to higher inefficiency in terms of fleet size a one is moving away from the global optimum achievable in the monopolistic market to an increasingly partial one. If the number of disjoint increases further the total size of the fleet would keep increasing owing to the lack of communication between mobility operators, even in the case when each of them try to optimize their fleet size based on the information about trip demand they service. The fact that considering two or three operators sharing equal shares of the mobility market results only in a small drop in efficiency in trms of the fleet size shows that the minimum fleet-size optimization using the network-based apprach for two or three independent operators is not far from the global optimum.
Fleet-size inflation due to rare events. The analysis of historical data has shown that our model provides a robust improvement (the reduction in fleet size) on previous models. However, an inflation of the optimal fleet size could occur as a result of rare, unusual demand pattern. For instance, if a sudden burst in the number of trips occurs around a given location but with diverging destinations, these trips will not be connected to each other in the vehicle-shareability network. Thus, for such cases to be served, the trips require separate vehicles form the existing pool on the road or even extra vehicles. These special events inflate the number of vehicles required because the nodes added to the vehicle-shareability network can have sparse or no connectivity to other nodes in the network. Although rare, such cases of trip-demand bursts can occur after events such as sports matches or concerts. However, based on our historical analysis it is evident that these outlying patterns only rarely lead to any inflation in the number of vehicles required to serve all the demand.
Data and code availability. All data processed during the course of this study are included in this Letter and its Supplementary Information. The code for generating the shareability network and optimal dispatching is subject to licensing and could be made available upon request to the authors. New York City taxi data used in the study can be downloaded at http://www.nyc.gov/html/tlc/html/about/trip_record_data.shtml.