代码 rbf分类_围观SVM模型在分类和预测问题上的强悍表现！

01

前言

在上一期的《手把手教你如何由浅入深地理解线性SVM模型》中我们分享了线性SVM模型的来龙去脉，得到很多读者朋友的点赞和支持，本期我们继续分享SVM模型的其他知识，即两个实战的案例，分别用于解决分类问题和预测问题。本文所使用到的数据集，读者朋友可以在文末找到下载链接。

02

分类问题的解决

本实战部分所使用的数据集是关于手体字母的识别，当一个用户在设备中写入某个字母后，该设备就需要准确地识别并返回写入字母的实际值。很显然，这是一个分类问题，即根据写入字母的特征信息(如字母的宽度、高度、边际等)去判断其属于哪一种字母。该数据集一共包含20 000个观测和17个变量，其中变量letter为因变量，具体的值就是20个英文字母。接下来利用SVM模型对该数据集的因变量做分类判断。

首先使用线性可分SVM对手体字母数据集建模，由于该模型会受到惩罚系数C的影响，故应用交叉验证的方法，从给定的几种C值中筛选出一个相对合理的，代码如下：

# 导入第三方模块
from sklearn import svm
import pandas as pd
from sklearn import model_selection
from sklearn import metrics

# 读取外部数据
letters = pd.read_csv(r'C:\Users\Administrator\Desktop\letterdata.csv')
# 数据前5行，见表13-1
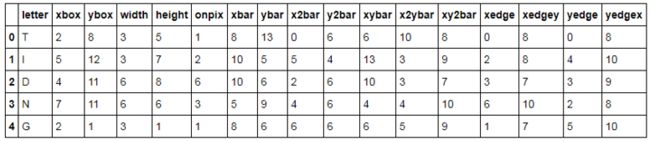
letters.head()

上表中反映了手体字母数据集的前5行观测，都是关于手写体的长、宽及坐标信息特征。通常在建模前都需要将原始数据集拆分为两个部分，分别用于模型的构建和测试，具体代码如下：

# 将数据拆分为训练集和测试集
predictors = letters.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(
                                            letters[predictors],                                             
                                            letters.letter,
                                            test_size = 0.25, 
                                            random_state = 1234)
# 使用网格搜索法，选择线性可分SVM“类”中的最佳C值
C=[0.05,0.1,0.5,1,2,5]
parameters = {
      'C':C}
grid_linear_svc = model_selection.GridSearchCV(estimator = svm.LinearSVC(),
                                        param_grid =parameters,
                                        scoring='accuracy',cv=5,verbose =1)
# 模型在训练数据集上的拟合
grid_linear_svc.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
grid_linear_svc.best_params_, grid_linear_svc.best_score_

out:
({
      'C': 0.1}, 0.69153333333333333)

# 模型在测试集上的预测
pred_linear_svc = grid_linear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test, pred_linear_svc)

out:
0.71479999999999999

如上结果所示，经过5重交叉验证后，发现最佳的惩罚系数C为0.1，模型在训练数据集上的平均准确率只有69.2%，同时，其在测试数据集的预测准确率也不足72%，说明线性可分SVM模型并不太适合该数据集的拟合和预测。接下来，使用非线性SVM模型对该数据集进行重新建模，代码如下：

# 使用网格搜索法，选择非线性可分SVM“类”中的最佳C值和核函数
kernel=['rbf','linear','poly','sigmoid']
C=[0.1,0.5,1,2,5]
parameters = {
      'kernel':kernel,'C':C}
grid_svc = model_selection.GridSearchCV(estimator = svm.SVC(),
                                   param_grid =parameters,
                                   scoring='accuracy',cv=5,verbose =1)
# 模型在训练数据集上的拟合
grid_svc.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
grid_svc.best_params_, grid_svc.best_score_

out:
({
      'C': 5, 'kernel': 'rbf'}, 0.97340000000000004)

# 模型在测试集上的预测
pred_svc = grid_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)

out:
0.9788

如上结果所示，经过5重交叉验证后，发现最佳的惩罚系数C为5，最佳的核函数为径向基核函数。相比于线性可分SVM模型来说，基于核技术的SVM表现了极佳的效果，模型在训练数据集上的平均准确率高达97.34%，而且其在测试数据集的预测准确率也接近98%，说明利用非线性可分SVM模型拟合及预测手体字母数据集是非常理想的。

03

预测问题的解决

本实战部分所使用的数据集来源于UCI网站，是一个关于森林火灾方面的预测，该数据集一共包含517条火灾记录和13个变量，其中变量area为因变量，表示火灾产生的森林毁坏面积，其余变量主要包含火灾发生的坐标位置、时间、各项火险天气指标、气温、湿度、风力等信息。接下来利用SVM模型对该数据集的因变量做预测分析：

# 读取外部数据
forestfires = pd.read_csv(r'C:\Users\Administrator\Desktop\forestfires.csv')
# 数据前5行，见表13-2。
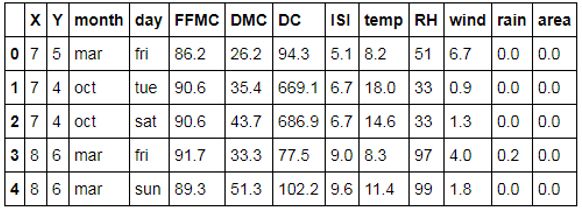
forestfires.head()

如上表所示，火灾发生的时间(month和day)为字符型的变量，如果将这样的变量带入模型中，就必须对其做数值化转换。考虑到月份可能是火灾发生的一个因素，故将该变量做保留处理，而将day变量删除。数据清洗如下：

# 删除day变量
forestfires.drop('day',axis = 1, inplace = True)
# 将月份做数值化处理
forestfires.month = pd.factorize(forestfires.month)[0]
# 预览数据前5行
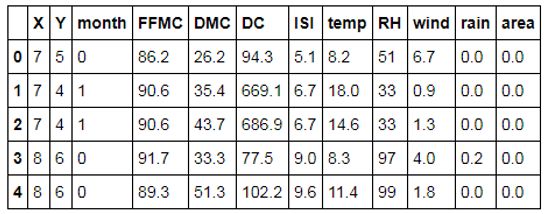
forestfires.head()

如上表所示，day变量已被删除，而且month变量也成为数值型变量。表中的应变量为area，是一个数值型变量，通常都需要对连续型的因变量做分布的探索性分析，如果数据呈现严重的偏态，而不做任何的修正时，直接带入到模型将会产生很差的效果。不妨这里使用直方图直观感受area变量的分布形态，操作代码如下：

# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import norm

# 绘制森林烧毁面积的直方图
sns.distplot(forestfires.area, bins = 50, kde = True, fit = norm, 
            hist_kws = {
      'color':'steelblue'}, 
               kde_kws = {
      'color':'red', 'label':'Kernel Density'}, 
               fit_kws = {
      'color':'black','label':'Nomal', 'linestyle':'--'})
# 显示图例
plt.legend()
# 显示图形
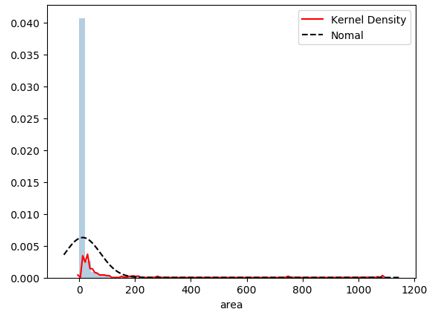
plt.show()

如上图所示，从分布来看，数据呈现严重的右偏。建模时不能够直接使用该变量，一般都会将数据做对数处理，代码如下：

# 导入第三方模块
from sklearn import preprocessing
import numpy as np

# 对area变量做对数变换
y = np.log1p(forestfires.area)
# 将X变量做标准化处理
predictors = forestfires.columns[:-1]
X = preprocessing.scale(forestfires[predictors])

接下来基于上面清洗后的数据将其拆分为两部分，分别用于模型的构建和测试。需要注意的是，在建模时必须对参数C、和y做调优处理，因为默认的SVM模型参数并不一定是最好的。代码如下：

# 将数据拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)

# 构建默认参数的SVM回归模型
svr = svm.SVR()
# 模型在训练数据集上的拟合
svr.fit(X_train,y_train)
# 模型在测试上的预测
pred_svr = svr.predict(X_test)
# 计算模型的MSE
metrics.mean_squared_error(y_test,pred_svr)

out:
1.9258635953335212

# 使用网格搜索法，选择SVM回归中的最佳C值、epsilon值和gamma值
epsilon = np.arange(0.1,1.5,0.2)
C= np.arange(100,1000,200)
gamma = np.arange(0.001,0.01,0.002)
parameters = {
      'epsilon':epsilon,'C':C,'gamma':gamma}
grid_svr = model_selection.GridSearchCV(estimator = svm.SVR(),param_grid =parameters,
                                               scoring='neg_mean_squared_error',
                                   cv=5,verbose =1, n_jobs=2)
# 模型在训练数据集上的拟合
grid_svr.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
print(grid_svr.best_params_, grid_svr.best_score_)

out:
{
      'C': 300, 'gamma': 0.001, 'epsilon': 1.1000000000000003} -1.99405794977

# 模型在测试集上的预测
pred_grid_svr = grid_svr.predict(X_test)
# 计算模型在测试集上的MSE值
metrics.mean_squared_error(y_test, pred_grid_svr)

out:
1.7455012238826526

如上结果所示，经过5重交叉验证后，非线性SVM回归的最佳惩罚系数C为300、最佳的值为1.1、最佳的Y值为0.001，而且模型在训练数据集上的负MSE值为-1.994。为了实现模型之间拟合效果的对比，构建了一个不做任何参数调整的SVM回归模型，并计算得到该模型在测试数据集上的MSE值为1.926，相比于经过调参之后的模型来说，这个值要高于1.746。进而可以说明，在利用SVM模型解决分类或预测问题时，需要对模型的参数做必要的优化。

04

结语

OK，本文的案例实战分享就到这里，如果你有任何问题，欢迎在公众号的留言区域表达你的疑问。同时，也欢迎各位朋友继续转发与分享文中的内容，让更多的人学习和进步。

05

广而告之

听说北京外国语大学国际商学院历时2年重磅打造了《商业数据分析》的在职研究生课程。知名企业+实战讲师，行业前沿观点+丰富校友资源，多维度精细化教学，更适合作为互联网从业者的你！

你将收获：

1.知名双一流院校硕士学位

2.行业领先实战技术

3.颠覆性的思维改变

4.高端人脉交流圈