【人脸】人脸矫正相关知识

目录

人脸矫正相关知识

一、人脸矫正的简要流程

二、Python代码中人脸矫正实现方式

三、C++代码中人脸矫正实现方式

---

人脸矫正相关知识

一、人脸矫正的简要流程

Step1、使用人脸检测结果的5个特征点和人脸标准的5个参考特征点坐标求出仿射变换矩阵。

Step2、通过上一步求得的放射变换矩阵对人脸进行旋转平移矫正，得到矫正好的人脸。

补充1.人脸标准的5个参考特征点坐标如下(人脸尺寸为112 * 112)：

    src = np.array([
      [30.2946+8.0, 51.6963],
      [65.5318+8.0, 51.5014],
      [48.0252+8.0, 71.7366],
      [33.5493+8.0, 92.3655],
      [62.7299+8.0, 92.2041] ], dtype=np.float32 )
#该特征点坐标是基于112*112尺寸人脸的

二、Python代码中人脸矫正实现方式

备注：该方法使用skimage库的transform.SimilarityTransform()，先计算仿射变换矩阵，再使用opencv中的warpAffine()函数矫正人脸图片。

src = np.array([
      [30.2946, 51.6963],
      [65.5318, 51.5014],
      [48.0252, 71.7366],
      [33.5493, 92.3655],
      [62.7299, 92.2041] ], dtype=np.float32 )
    if image_size[1]==112:
      src[:,0] += 8.0 #每一行的第0个数据
    dst = landmark.astype(np.float32) #astype:数据类型转换
    
    # step1.计算仿射变换举证
    tform = trans.SimilarityTransform() #创建一个相似变换对象(这是用到python的skimage库)
    tform.estimate(dst, src)  # estimate():通过一组对应点估计出变换矩阵
    M = tform.params[0:2,:]
    # M = trorm.params
    
    # step2.通过仿射变换矩阵对人脸进行矫正
    warped = cv2.warpAffine(img,M,(image_size[1],image_size[0]), borderValue = 0.0)

    ### 这里还看到有一个投影变换的操作方法,不过并未使用该方法
    tform3 = trans.ProjectiveTransform()
    tform3.estimate(src, dst)
    warped = trans.warp(img, tform3, output_shape=_shape)

三、C++代码中人脸矫正实现方式

备注：C++中直接使用opencv库函数实现人脸矫正功能。

//pts为人脸检测结果的特征点坐标,anchors是标准参考特征点坐标
///===step1.计算仿射变换矩阵
cv::Mat warp_mat = cv::estimateRigidTransform(pts, anchors, false);    //求特征点的仿射变换矩阵

///===step2.通过仿射变换矩阵矫正人脸
cv::warpAffine(imgc, rectifiedImg, warp_mat, cv::Size(112, 112));//对图像的旋转和平移都是通过仿射变换函数cv::warpAffine()来实现的

备注：cvEstimateRigidTransform是opencv中求取仿射变换的函数，该函数会用到ransac算法（从所有特征点中通过迭代的方式选取若干数量的"有效"特征点），然后利用icvGetRTMatrix函数求取仿射变换系数。

ransac算法简要介绍：

ransac算法能够解决全部的数据中存在错误数据的情况，现实中我们的数据可能会存在错误的数据(标注错误等等)，这些数据会影响模型拟合，ransac算法随机选取数据中的一部分进行迭代，有较大概率能够避开错误数据的干扰。

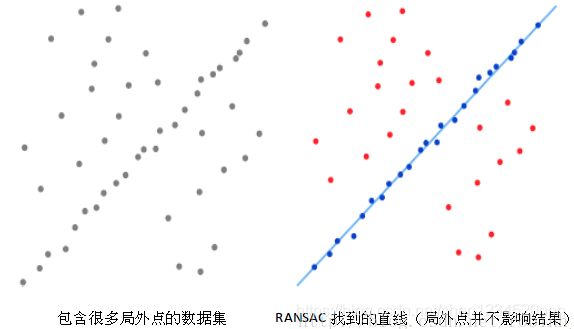
RANSAC算法通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：
1.首先我们先随机假设一小组局内点为初始值。然后用此局内点拟合一个模型。(此模型适应于假设的局内点，所有的未知参数都能从假设的局内点计算得出)。
2.用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点，将局内点扩充。
3.如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
4.然后，用所有假设的局内点去重新估计模型，因为此模型仅仅是在初始的假设的局内点估计的，后续有扩充后，需要更新。
5.最后，通过估计局内点与模型的错误率来评估模型。
整个这个过程为迭代一次，此过程被重复执行固定的次数，每次产生的模型有两个结局：
1、要么因为局内点太少，还不如上一次的模型，而被舍弃，
2、要么因为比现有的模型更好而被选用。
参考链接：https://blog.csdn.net/robinhjwy/article/details/79174914

 

下面还有一个第三方实现的仿射变换矩阵计算方法：(来源:https://blog.csdn.net/u011956147/article/details/90294249)

float default[5][2] = {  
            {30.2946f+8.0f, 51.6963f},
            {65.5318f+8.0f, 51.5014f},
            {48.0252f+8.0f, 71.7366f},
            {33.5493f+8.0f, 92.3655f},
            {62.7299f+8.0f, 92.2041f}
        };  // +8.0f for 112*112
float detect[5][2] = {  
            {30.2946f, 51.6963f},
            {65.5318f, 51.5014f},
            {48.0252f, 71.7366f},
            {33.5493f, 92.3655f},
            {62.7299f, 92.2041f}
        };  // 
cv::Mat src(5,2,CV_32FC1, default); 
memcpy(src.data, default, 2 * 5 * sizeof(float));
cv::Mat dst(5,2,CV_32FC1, detect);
memcpy(dst.data, detect, 2 * 5 * sizeof(float));

cv::Mat M = FacePreprocess::similarTransform(dst, src);  // skimage.transform.SimilarityTransform
cv::Mat warpImg;
//cv::warpAffine(input, warpImg, M, cv::Size(112, 112));
cv::warpPerspective(inpu, croppedMat, M, cv::Size(112, 112));

namespace FacePreprocess {

    cv::Mat meanAxis0(const cv::Mat &src)
    {
        int num = src.rows;
        int dim = src.cols;

        // x1 y1
        // x2 y2

        cv::Mat output(1,dim,CV_32F);
        for(int i = 0 ; i <  dim; i ++)
        {
            float sum = 0 ;
            for(int j = 0 ; j < num ; j++)
            {
                sum+=src.at(j,i);
            }
            output.at(0,i) = sum/num;
        }

        return output;
    }

    cv::Mat elementwiseMinus(const cv::Mat &A,const cv::Mat &B)
    {
        cv::Mat output(A.rows,A.cols,A.type());

        assert(B.cols == A.cols);
        if(B.cols == A.cols)
        {
            for(int i = 0 ; i <  A.rows; i ++)
            {
                for(int j = 0 ; j < B.cols; j++)
                {
                    output.at(i,j) = A.at(i,j) - B.at(0,j);
                }
            }
        }
        return output;
    }


    cv::Mat varAxis0(const cv::Mat &src)
    {
	cv::Mat temp_ = elementwiseMinus(src,meanAxis0(src));
        cv::multiply(temp_ ,temp_ ,temp_ );
        return meanAxis0(temp_);

    }



    int MatrixRank(cv::Mat M)
    {
	cv::Mat w, u, vt;
	cv::SVD::compute(M, w, u, vt);
	cv::Mat1b nonZeroSingularValues = w > 0.0001;
        int rank = countNonZero(nonZeroSingularValues);
        return rank;

    }

//    References
//    ----------
//    .. [1] "Least-squares estimation of transformation parameters between two
//    point patterns", Shinji Umeyama, PAMI 1991, DOI: 10.1109/34.88573
//
//    """
//
//    Anthor:Jack Yu
    cv::Mat similarTransform(cv::Mat src,cv::Mat dst) {
        int num = src.rows;
        int dim = src.cols;
        cv::Mat src_mean = meanAxis0(src);
        cv::Mat dst_mean = meanAxis0(dst);
        cv::Mat src_demean = elementwiseMinus(src, src_mean);
        cv::Mat dst_demean = elementwiseMinus(dst, dst_mean);
        cv::Mat A = (dst_demean.t() * src_demean) / static_cast(num);
        cv::Mat d(dim, 1, CV_32F);
        d.setTo(1.0f);
        if (cv::determinant(A) < 0) {
            d.at(dim - 1, 0) = -1;

        }
	cv::Mat T = cv::Mat::eye(dim + 1, dim + 1, CV_32F);
        cv::Mat U, S, V;
	cv::SVD::compute(A, S,U, V);

        // the SVD function in opencv differ from scipy .


        int rank = MatrixRank(A);
        if (rank == 0) {
            assert(rank == 0);

        } else if (rank == dim - 1) {
            if (cv::determinant(U) * cv::determinant(V) > 0) {
                T.rowRange(0, dim).colRange(0, dim) = U * V;
            } else {
//            s = d[dim - 1]
//            d[dim - 1] = -1
//            T[:dim, :dim] = np.dot(U, np.dot(np.diag(d), V))
//            d[dim - 1] = s
                int s = d.at(dim - 1, 0) = -1;
                d.at(dim - 1, 0) = -1;

                T.rowRange(0, dim).colRange(0, dim) = U * V;
                cv::Mat diag_ = cv::Mat::diag(d);
                cv::Mat twp = diag_*V; //np.dot(np.diag(d), V.T)
		cv::Mat B = cv::Mat::zeros(3, 3, CV_8UC1);
		cv::Mat C = B.diag(0);
                T.rowRange(0, dim).colRange(0, dim) = U* twp;
                d.at(dim - 1, 0) = s;
            }
        }
        else{
            cv::Mat diag_ = cv::Mat::diag(d);
            cv::Mat twp = diag_*V.t(); //np.dot(np.diag(d), V.T)
            cv::Mat res = U* twp; // U
            T.rowRange(0, dim).colRange(0, dim) = -U.t()* twp;
        }
        cv::Mat var_ = varAxis0(src_demean);
        float val = cv::sum(var_).val[0];
        cv::Mat res;
        cv::multiply(d,S,res);
        float scale =  1.0/val*cv::sum(res).val[0];
        T.rowRange(0, dim).colRange(0, dim) = - T.rowRange(0, dim).colRange(0, dim).t();
        cv::Mat  temp1 = T.rowRange(0, dim).colRange(0, dim); // T[:dim, :dim]
        cv::Mat  temp2 = src_mean.t(); //src_mean.T
        cv::Mat  temp3 = temp1*temp2; // np.dot(T[:dim, :dim], src_mean.T)
        cv::Mat temp4 = scale*temp3;
        T.rowRange(0, dim).colRange(dim, dim+1)=  -(temp4 - dst_mean.t()) ;
        T.rowRange(0, dim).colRange(0, dim) *= scale;
        return T;
    }
}