数据结构与算法python—13.堆及python实现与leetcode总结
文章目录
-
- 一、优先队列详解
-
- 1.优先队列的实现
- 二、堆
-
- 1.堆的两种实现
-
- 1.1 基于链表的实现-跳表
- 1.2 基于数组的实现-二叉堆
-
- 1.2.1 二叉堆的基本框架
- 1.2.2 向堆中添加元素和ShiftUp(上浮)
- 1.2.3 取出堆中的最大元素和Shift Down(下沉)
- 1.2.4 replace
- 1.2.5 heapity
- 1.2.6 测试过程
- 1.2.7 堆实现的全部代码
- 2.堆的一个中心
-
- 1046. 最后一块石头的重量
- 3.堆的三个技巧
-
- 295. 数据流的中位数
- 1439. 有序矩阵中的第 k 个最小数组和
- 264. 丑数 II
- 871. 最低加油次数
- 1642. 可以到达的最远建筑
一、优先队列详解
什么是优先队列?普通队列:先进先出;后进后出。而优先队列,顾名思义,优先队列:出队顺序和入队顺序无关;和优先级相关。优先队列与普通队列的区别在于出队顺序上。
那为什么要使用优先队列呢?因为并不是所有任务都是先到先得的,而是会动态选择优先级最高的任务去执行。比如操作系统会动态选择优先级最高的任务去执行。
1.优先队列的实现
优先队列与普通队列相比,只会在返回队首元素与出队方面有差别。优先队列可以使用普通线性结构来实现,比如数组与链表,此时出队需要扫描一遍线性结构,找到最大值,时间复杂度为 O ( n ) O(n) O(n),性能上不尽如人意。优先队列也可以使用顺序线性结构来实现,这里的顺序线性结构是指数据结构(数组或链表)本身维持着顺序,从大到小或者从小到大排列,此时出队将变得非常容易,时间复杂度为 O ( 1 ) O(1) O(1),而这种数据结构入队时,最差的情况时将整个数据结构扫描一遍才能找到插入位置,时间复杂度为 O ( n ) O(n) O(n)。这一章介绍的堆数据结构,入队与出队的时间复杂度均为 O ( l o g n ) O(logn) O(logn),这与二叉搜索树的时间复杂度不同,二叉搜索树的平均时间复杂度为 O ( l o g n ) O(logn) O(logn),所以堆数据结构是非常高效的
| 数据结构 | 入队 | 出队(拿出最大元素) |
|---|---|---|
| 普通线性结构 | O(1) | O(n) |
| 顺序线性结构 | O(n) | O(1) |
| 堆 | O(logn) | O(logn) |
二、堆
堆的核心内容:两种实现,一个中心,三个技巧。
1.堆的两种实现
这里介绍两种常见的堆实现,一种是基于链表的实现-跳表,另一种是基于数组的实现-二叉堆。
1.1 基于链表的实现-跳表
跳表的算法实现如果没有经过精雕细琢,性能很不稳定;而且当数据量增加时,跳表的内存占用会明显增加。所以跳表只讲述原理,不详细讲述代码实现。
基于链表实现的堆中,链表是有序的。
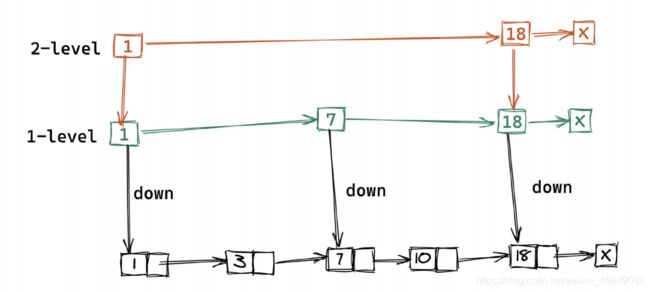
比如:想在跳表中查找10
一级跳表中7指向节点7,下一个18指向节点18,因此,10在节点7与节点18之间,通过down指针回到原始链表中找到了节点7,节点7的next指针即为节点10.
在上例的基础上,如果数据量继续增大,那么索引层数也会继续增大1-level,2-level,...n-level,最终可以使链表实现二分查找,也就可以获得更好的效率,当然不可避免的增加了空间复杂度。
跳表的时间复杂度为索引的层数 * 平均每层索引遍历的个数,其中索引的层数为二分查找的时间复杂度 O ( l o g n ) O(logn) O(logn),而平均每层索引遍历的个数是个常数,因此跳表的时间复杂度为 O ( l o g n ) O(logn) O(logn)。空间复杂度等同于索引节点的总个数 O ( n ) O(n) O(n)。
跳表的入堆与出堆操作:
- 入堆操作,只需要根据索引插到链表中,并更新索引
- 出堆操作,只需要删除头部(或者尾部),并更新索引
具体实现可以参考leetcode—1206. 设计跳表
1.2 基于数组的实现-二叉堆
-
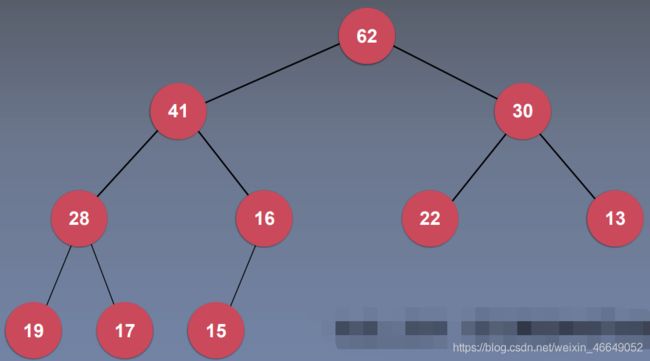
二叉堆是一颗完全二叉树
-
二叉堆的性质:
最大堆:堆中某个节点的值总是不大于其父节点的值(并不要求上一层的值都大于下一层的值)
最小堆:堆中某个节点的值总是不小于其父节点的值
-
二叉堆的实现,我们可以使用二叉搜索树的实现方式来实现,同样我们可以用数组的形式来实现完全二叉树。
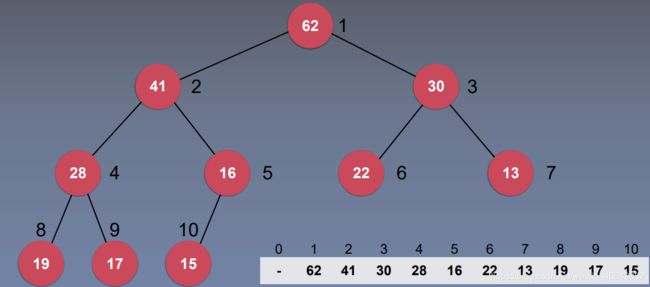
现在的问题就变成:用数组形式实现完全二叉树时,应该怎么找到每一个父节点的左右孩子?
很容易发现,在数组中,若父节点的索引为 n n n,则左孩子的索引为 2 n 2n 2n,右孩子的索引为 2 n + 1 2n+1 2n+1。若左或右孩子的索引为 n n n,则父节点的索引为 n 2 \frac{n}2 2n。p a r e n t ( i ) = i / 2 parent(i) = i / 2 parent(i)=i/2
l e f t c h i l d ( i ) = 2 ∗ i left child (i) = 2*i leftchild(i)=2∗i
r i g h t c h i l d ( i ) = 2 ∗ i + 1 rightchild(i ) =2*i +1 rightchild(i)=2∗i+1若二叉搜索树的索引从0开始,则
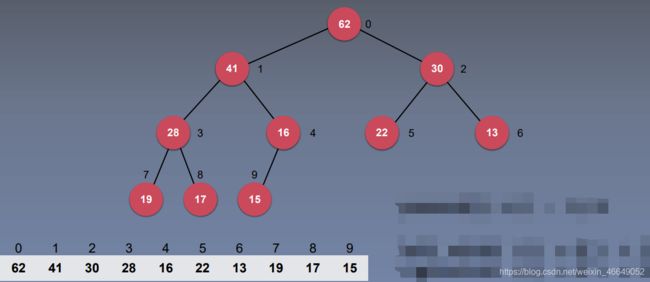
在数组中,若父节点的索引为 n n n,则左孩子的索引为 2 n + 1 2n+1 2n+1,右孩子的索引为 2 n + 2 2n+2 2n+2。若左或右孩子的索引为 n n n,则父节点的索引为 n − 1 2 \frac{n-1}2 2n−1。
1.2.1 二叉堆的基本框架
# 创建最大堆
class MaxHeap:
def __init__(self, arr=None, capacity=None):
# 如果数组容量为空
if not capacity:
self._data = Array()
# 如果容量不为空
else:
self._data = Array(capacity=capacity)
# 判断堆尺寸
def size(self):
return self._data.get_size()
# 判断堆是否为空
def is_empty(self):
return self._data.is_empty()
# 返回完全二叉树数组表示中,一个索引所表示的元素的父亲节点的索引 (i - 1)// 2
def _parent(self, index):
if index == 0:
raise ValueError('index-0 doesn\'t have parent.')
return (index - 1) // 2
# 返回完全二叉树数组表示中,一个索引所表示的元素的左孩子节点的索引 2 * i + 1
def _left_child(self, index):
return index * 2 + 1
# 返回完全二叉树数组表示中,一个索引所表示的元素的右孩子节点的索引 2 * i + 2
def _right_child(self, index):
return index * 2 + 2
1.2.2 向堆中添加元素和ShiftUp(上浮)
def add(self, e):
# 将元素添加到末尾
self._data.add_last(e)
# 上浮以满足最大堆的性质
# self._data.get_size() - 1为添加到末尾的元素的索引
self._sift_up(self._data.get_size() - 1)
# 上浮—当插入到数组末尾不满足最大堆结构时,说明这个元素比父节点大,需要上浮
# 将这个节点与父节点、父节点的父节点进行比较,如果这个节点大,则进行交换,直至这个节点小于其父节点
def _sift_up(self, k):
# 循环结束条件是k<=0或者小于父节点
while k > 0 and self._data.get(k) > self._data.get(self._parent(k)):
# k与父节点互换
self._data.swap(k, self._parent(k))
# k移到父节点索引上
k = self._parent(k)
1.2.3 取出堆中的最大元素和Shift Down(下沉)
add和extractMax时间复杂度都是O(logn)
# 找到堆中最大的元素,返回索引为0的元素
def find_max(self):
if self._data.get_size() == 0:
raise ValueError('Can not find_max when heap is empty.')
return self._data.get(0)
# 返回堆的最大元素,并调整堆的结构以满足最大堆的性质
def extract_max(self):
# 取出最大元素
ret = self.find_max()
# 将索引0处的元素与最后一个元素互换一下位置
self._data.swap(0, self._data.get_size() - 1)
# 删除最后一个元素
self._data.remove_last()
# 此时索引0处的元素比它左右孩子节点的元素小,需要下沉
self._sift_down(0)
return ret
# 下沉
def _sift_down(self, k):
# 循环结束的条件是k的左孩子的索引大于等于尺寸
while self._left_child(k) < self._data.get_size():
j = self._left_child(k)
# 如果右孩子存在,并且右孩子的值大于左孩子的值,则k与其右孩子互换元素,否则与其左孩子互换元素
if j + 1 < self._data.get_size() and self._data.get(j + 1) > self._data.get(j):
# 说明右孩子的值比左孩子的值大
j = self._right_child(k)
# 此时self._data.get(j)是左孩子和右孩子中的最大值
if self._data.get(k) > self._data.get(j):
break
self._data.swap(k, j)
# 将k移动到其孩子节点上来
k = j
1.2.4 replace
replace:取出最大元素后,放入一个新元素
实现:可以先extractMax,再add,两次O(logn)的操作
实现:可以直接将堆顶元素替换以后Shift Down,一次O(logn)的操作
# 取出最大元素后,放入一个新元素
def replace(self, e):
# 找到最大值元素
ret = self.find_max()
# 这样可以一次logn完成
# 将最大值元素与新元素进行互换
self._data.set(0, e)
# 将新元素下沉,直到满足最大堆的性质
self._sift_down(0)
return ret
1.2.5 heapity
heapify:将任意数组整理成堆的形状。从非叶子节点开始,从后向前,不断对这些非叶子节点进行下沉。
将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn)
heapify的过程,算法复杂度为O(n)
class MaxHeap:
def __init__(self, arr=None, capacity=None):
if isinstance(arr, Array):
self._data = arr
# 从非叶子节点开始,从后向前,不断对这些节点进行下沉
for i in range(self._parent(arr.get_size() - 1), -1, -1):
self._sift_down(i)
return
# 如果数组容量为空
if not capacity:
self._data = Array()
# 如果容量不为空
else:
self._data = Array(capacity=capacity)
1.2.6 测试过程
if __name__ == '__main__':
n = 10000
from time import time
start_time1 = time()
max_heap = MaxHeap()
from random import randint
for i in range(n):
max_heap.add(randint(0, 1000))
print('heap add: ', time() - start_time1)
start_time2 = time()
arr = Array()
from random import randint
for i in range(n):
arr.add_last(randint(0, 1000))
max_heap = MaxHeap(arr)
print('heapify: ', time() - start_time2)
heap add: 0.13298821449279785
heapify: 0.10198855400085449
1.2.7 堆实现的全部代码
# 创建最大堆
class MaxHeap:
def __init__(self, arr=None, capacity=None):
if isinstance(arr, Array):
self._data = arr
# 从非叶子节点开始,从后向前,不断对这些节点进行下沉
for i in range(self._parent(arr.get_size() - 1), -1, -1):
self._sift_down(i)
return
# 如果数组容量为空
if not capacity:
self._data = Array()
# 如果容量不为空
else:
self._data = Array(capacity=capacity)
# 判断堆尺寸
def size(self):
return self._data.get_size()
# 判断堆是否为空
def is_empty(self):
return self._data.is_empty()
# 返回完全二叉树数组表示中,一个索引所表示的元素的父亲节点的索引 (i - 1)// 2
def _parent(self, index):
if index == 0:
raise ValueError('index-0 doesn\'t have parent.')
return (index - 1) // 2
# 返回完全二叉树数组表示中,一个索引所表示的元素的左孩子节点的索引 2 * i + 1
def _left_child(self, index):
return index * 2 + 1
# 返回完全二叉树数组表示中,一个索引所表示的元素的右孩子节点的索引 2 * i + 2
def _right_child(self, index):
return index * 2 + 2
def add(self, e):
# 将元素添加到末尾
self._data.add_last(e)
# 上浮以满足最大堆的性质
# self._data.get_size() - 1为添加到末尾的元素的索引
self._sift_up(self._data.get_size() - 1)
# 上浮—当插入到数组末尾不满足最大堆结构时,说明这个元素比父节点大,需要上浮
# 将这个节点与父节点、父节点的父节点进行比较,如果这个节点大,则进行交换,直至这个节点小于其父节点
def _sift_up(self, k):
# 循环结束条件是k<=0或者小于父节点
while k > 0 and self._data.get(k) > self._data.get(self._parent(k)):
# k与父节点互换
self._data.swap(k, self._parent(k))
# k移到父节点索引上
k = self._parent(k)
# 找到堆中最大的元素,返回索引为0的元素
def find_max(self):
if self._data.get_size() == 0:
raise ValueError('Can not find_max when heap is empty.')
return self._data.get(0)
# 返回堆的最大元素,并调整堆的结构以满足最大堆的性质
def extract_max(self):
# 取出最大元素
ret = self.find_max()
# 将索引0处的元素与最后一个元素互换一下位置
self._data.swap(0, self._data.get_size() - 1)
# 删除最后一个元素
self._data.remove_last()
# 此时索引0处的元素比它左右孩子节点的元素小,需要下沉
self._sift_down(0)
return ret
# 下沉
def _sift_down(self, k):
# 循环结束的条件是k的左孩子的索引大于等于尺寸
while self._left_child(k) < self._data.get_size():
j = self._left_child(k)
# 如果右孩子存在,并且右孩子的值大于左孩子的值,则k与其右孩子互换元素,否则与其左孩子互换元素
if j + 1 < self._data.get_size() and self._data.get(j + 1) > self._data.get(j):
# 说明右孩子的值比左孩子的值大
j = self._right_child(k)
# 此时self._data.get(j)是左孩子和右孩子中的最大值
if self._data.get(k) > self._data.get(j):
break
self._data.swap(k, j)
# 将k移动到其孩子节点上来
k = j
# 取出最大元素后,放入一个新元素
def replace(self, e):
# 找到最大值元素
ret = self.find_max()
# 这样可以一次logn完成
# 将最大值元素与新元素进行互换
self._data.set(0, e)
# 将新元素下沉,直到满足最大堆的性质
self._sift_down(0)
return ret
if __name__ == '__main__':
n = 10000
from time import time
start_time1 = time()
max_heap = MaxHeap()
from random import randint
for i in range(n):
max_heap.add(randint(0, 1000))
print('heap add: ', time() - start_time1)
start_time2 = time()
arr = Array()
from random import randint
for i in range(n):
arr.add_last(randint(0, 1000))
max_heap = MaxHeap(arr)
print('heapify: ', time() - start_time2)
2.堆的一个中心
这里先介绍两个概念:
-
使用堆不仅仅可以存储单一值,比如[1,2,3,4]的1,2,3,4分别都是单一值。除了单一值,也可以存储复合值,比如对象或者元组等。
[(1,2,3),(4,5,6),(2,1,3),(4,2,8)]import heapq # 如果元祖的第一位相同,则比较第二位,大的就大 h = [(1, 2, 3), (4, 5, 6), (2, 1, 3), (4, 2, 8)] heapq.heapify(h) # 堆化(小顶堆) heapq.heappop(h) # 弹出(1,2,3) heapq.heappop(h) # 弹出(2,1,3) heapq.heappop(h) # 弹出(4,2,8) heapq.heappop(h) # 弹出(4,5,6) -
模拟大顶堆:由于Python没有大顶堆(只有小顶堆)。因此我这里使用了小顶堆进行模拟实现。即将原有的数全部取相反数,比如原数字是5,就将-5入堆。经过这样的处理,小顶堆就可以当成大顶堆用了。不过需要注意的是,当你 pop 出来的时候,记得也要取反,将其还原回来哦。
import heapq # 模拟最大堆,利用小顶堆模拟大顶堆时,入堆需要取相反数,出堆也需要取相反数 h = [] A = [1, 2, 3, 4, 5] for a in A: heapq.heappush(h, -a) print(h) # [-5, -4, -2, -1, -3] -1 * heapq.heappop(h) # 5 -1 * heapq.heappop(h) # 4 -1 * heapq.heappop(h) # 3 -1 * heapq.heappop(h) # 2 -1 * heapq.heappop(h) # 1
堆的中心就是动态求极值,动态与极值缺一不可。
1046. 最后一块石头的重量
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出两块 最重的 石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下,就返回 0。
示例:
输入:[2,7,4,1,8,1]
输出:1
解释:
先选出 7 和 8,得到 1,所以数组转换为 [2,4,1,1,1],
再选出 2 和 4,得到 2,所以数组转换为 [2,1,1,1],
接着是 2 和 1,得到 1,所以数组转换为 [1,1,1],
最后选出 1 和 1,得到 0,最终数组转换为 [1],这就是最后剩下那块石头的重量。
思路:
利用小顶堆模拟大顶堆时,入堆需要取相反数,出堆也需要取相反数
class Solution:
def lastStoneWeight(self, stones: List[int]) -> int:
# 利用python小顶堆构造大顶堆
heap = [-stone for stone in stones]
# 构建二叉堆
heapq.heapify(heap)
while len(heap) > 1:
# 依次弹出两个头部元素
x,y = heapq.heappop(heap),heapq.heappop(heap)
if x != y:
#同时添加到列表与堆中
heapq.heappush(heap,x-y)
if heap:
return -heap[0]
return 0
3.堆的三个技巧
技巧一:固定堆
这个技巧指的是固定堆的大小 k k k不变,代码上可通过每 pop出去一个就 push进来一个来实现。而由于初始堆可能是0,我们刚开始需要一个一个 push 进堆以达到堆的大小为 k k k,因此严格来说应该是维持堆的大小不大于 k k k。
这个技巧可以用到求第k小的值或者求第k大的值。
比如:求第k小的值
思路:建立一个大顶堆,维持堆的大小为k,如果新入队后,堆的大小大于k,则与新入队元素与堆顶比较,将较大的数移除,这样就可以保证堆中的元素是全体元素中最小的k个,此时,堆顶元素为第k小的值。堆是最小的k个数,堆顶又是最大的,因此堆顶就是第k小的
总结来说:
- 固定大小为k的大顶堆,可以快速求第k小的值
- 固定大小为k的小顶堆,可以快速求第k大的值
295. 数据流的中位数
这道题基于固定堆技巧,利用大顶堆与小顶堆的性质就可以快速找到中位数。比如:数据个数为 n n n,大顶堆元素个数为 n + 1 2 \frac{n+1}2 2n+1,小顶堆元素个数 n − n + 1 2 n-\frac{n+1}2 n−2n+1,那么 0 < = n + 1 2 − ( n − n + 1 2 ) < = 1 0<=\frac{n+1}2-(n-\frac{n+1}2)<=1 0<=2n+1−(n−2n+1)<=1,当n为奇数时, = 1 =1 =1。
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中。
- double findMedian() - 返回目前所有元素的中位数。
进阶:
- 如果数据流中所有整数都在 0 到 100 范围内,你将如何优化你的算法?
- 如果数据流中 99% 的整数都在 0 到 100 范围内,你将如何优化你的算法?
示例:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
思路1:两个堆
将一个有序数组分为前有序数组与后有序数组
然后利用前有序数组构造最大堆,利用后有序数组构造最小堆
此时,最大堆与最小堆有两个性质:
- 最大堆堆顶元素小于最小堆堆顶元素
- 最大堆元素个数要么与最小堆元素个数相等,要么多一个元素
具体操作:
- 情况1:当两个堆的元素个数之和为偶数,为了让最大堆中多1个元素采用这样的流程:「最大堆→最小堆→最大堆」;
- 情况2:当两个堆的元素个数之和为奇数,此时最小堆必须多1个元素,这样最大堆和最小堆的元素个数才相等,采用这样的流程:「最大堆→最小堆]即可。
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
# 初始化元素个数之和,最大堆,最小堆
self.count = 0
self.max_heap = []
self.min_heap = []
# 往最大堆与最小堆中添加元素,元素个数为奇数与偶数时不同
def addNum(self, num: int) -> None:
self.count += 1
# python中定义的是小顶堆,所以需要传入相反数,来模拟大顶堆
heapq.heappush(self.max_heap,(-num,num))
# 弹出大顶堆堆顶元素
_,max_heap_top = heapq.heappop(self.max_heap)
# 构造小顶堆
heapq.heappush(self.min_heap,max_heap_top)
# 如果元素个数为奇数,则大顶堆元素个数比小顶堆多1个
if self.count & 1:
# 弹出小顶堆堆顶元素
min_heap_top = heapq.heappop(self.min_heap)
# 将小顶堆堆顶元素压入大顶堆
heapq.heappush(self.max_heap,(-min_heap_top,min_heap_top))
def findMedian(self) -> float:
# 如果元素个数为奇数,则中位数为大顶堆堆顶元素
if self.count & 1:
return self.max_heap[0][1]
# 如果元素个数为偶数,则中位数为大顶堆与小顶堆对顶元素的平均值
else:
return (self.max_heap[0][1] + self.min_heap[0]) / 2
技巧二:多路归并
多路体现在:有多条候选路线。代码上,我们可使用多指针来表示。归并体现在:结果可能是多个候选路线中最长的或者最短,也可能是第k个等。因此我们需要对多条路线的结果进行比较,并根据题目描述舍弃或者选取某一个或多个路线。
1439. 有序矩阵中的第 k 个最小数组和
给你一个
m * n的矩阵 mat,以及一个整数k,矩阵中的每一行都以非递减的顺序排列。
你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个最小数组和。
示例:
输入:mat = [[1,3,11],[2,4,6]], k = 5
输出:7
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。
class Solution:
def kthSmallest(self, mat: List[List[int]], k: int) -> int:
# 初始化堆
h = []
# 元祖cur有两个信息组成,一个是m个一维数组首项和,表示数组和,一个是长度为m且全部填充为0的元祖,表示数组指针
cur = (sum(vec[0] for vec in mat),tuple([0]*len(mat)))
# 将元祖cur入堆
heapq.heappush(h,cur)
# 避免同样的指针被计算多次
seen = set(cur)
for _ in range(k):
# acc表示当前和,pointer是指针情况
acc,pointers = heapq.heappop(h)
# 每次都粗暴地移动指针数组中的一个指针。每移动一个指针就分叉一次,一共可能移动的情况是n,其中 n为一维数组的长度。
for i,pointer in enumerate(pointers):
# 如果 pointer == len(mat[0]) - 1 说明到头了,不能移动了
if pointer != len(mat[0]) - 1:
# 如果没有到头,那么指针移动一位,此时要判断我们要移动的指针有没有出现在哈希表里面
t = list(pointers)
t[i] = pointer + 1
tt = tuple(t)
# 如果已经出现在哈希表里面,则跳过,否则,添加到哈希表里面
if tt not in seen:
seen.add(tt)
# 加入堆
heapq.heappush(h,(acc + mat[i][pointer + 1]- mat[i][pointer], tt))
return acc
264. 丑数 II
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。
示例:
输入:n = 10
输出:12
解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
思路1:优先队列(小根堆)
一个简单的解法是使用优先队列
- 起始先将最小丑数1放入队列形
- 每次从队列取出最小值x,然后将x 所对应的丑数2x、3x和5x进行入队。
- 对步骤⒉循环多次,第n次出队的值即是答案。
为了防止同一丑数多次进队,我们需要使用数据结构Set来记录入过队列的丑数。
class Solution:
def nthUglyNumber(self, n: int) -> int:
nums = [2,3,5]
# 使用哈希表记录入堆的丑数,防止同一丑数多次入堆
explored = {
1}
# 最小堆记录丑数
pq = [1]
for i in range(1,n+1):
# 从堆中取出最小值
x = heapq.heappop(pq)
# i==n表示第n次出队
if i == n:
return x
for num in nums:
t = num * x
# 如果新生成的丑数还没有入堆,则添加到哈希表中与最小堆中
if t not in explored:
explored.add(t)
heapq.heappush(pq,t)
class Solution:
def nthUglyNumber(self, n: int) -> int:
# ans用作存储已有丑数
ans = [0] * (n+1)
# 从下标1开始存储,第一个丑数为1
ans[1] = 1
#由于三个有序序列都是由 已有丑数 * 质因数 而来
# i2、i3和 i5 分别代表三个有序序列当前使用到哪一位 已有丑数 下标(起始都指向1)
i2 = i3= i5 = 1
idx = 2
while idx <= n:
# 由ans[ix]*X可得当前有序序列指向哪一位
a,b,c = ans[i2]*2,ans[i3]*3,ans[i5]*5
# 将三个有序序列中的最小一位存入已有丑数序列,并将其下标后移
m = min(a,b,c)
if m == a:
i2 += 1
if m == b:
i3 += 1
if m == c:
i5 += 1
ans[idx] = m
# ans下标后移
idx += 1
# 循环结束条件为idx = n+1
return ans[n]
技巧三:事后小诸葛
这个技巧指的是:当从左到右遍历的时候,我们是不知道右边是什么的,需要等到你到了右边之后才知道。如果想知道右边是什么,一种简单的方式是遍历两次,第一次遍历将数据记录下来,当第二次遍历的时候,用上次遍历记录的数据。这是我们使用最多的方式。不过有时候,我们也可以在遍历到指定元素后,往前回溯,这样就可以边遍历边存储,使用一次遍历即可。
具体来说就是将从左到右的数据全部收集起来,等到需要用的时候,从里面挑一个用。如果我们都要取最大值或者最小值且极值会发生变动,就可使用堆加速。直观上就是使用了时光机回到之前,达到了事后诸葛亮的目的。
871. 最低加油次数
汽车从起点出发驶向目的地,该目的地位于出发位置东面
target英里处。
沿途有加油站,每个station[i]代表一个加油站,它位于出发位置东面station[i][0]英里处,并且有station[i][1]升汽油。
假设汽车油箱的容量是无限的,其中最初有startFuel升燃料。它每行驶 1 英里就会用掉 1 升汽油。
当汽车到达加油站时,它可能停下来加油,将所有汽油从加油站转移到汽车中。
为了到达目的地,汽车所必要的最低加油次数是多少?如果无法到达目的地,则返回 -1 。
注意:
如果汽车到达加油站时剩余燃料为 0,它仍然可以在那里加油。如果汽车到达目的地时剩余燃料为 0,仍然认为它已经到达目的地。
示例:
输入:target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
输出:2
解释:
我们出发时有 10 升燃料。
我们开车来到距起点 10 英里处的加油站,消耗 10 升燃料。将汽油从 0 升加到 60 升。
然后,我们从 10 英里处的加油站开到 60 英里处的加油站(消耗 50 升燃料),
并将汽油从 10 升加到 50 升。然后我们开车抵达目的地。
我们沿途在1两个加油站停靠,所以返回 2 。
思路:事后诸葛亮
先遍历一遍station,然后构造大顶堆,每次判断当前汽油够不够到达下一个汽油站,如果够的话,则继续;如果不够,则选择在已经走过的位置中汽油最多的站中加油
class Solution:
def minRefuelStops(self, target: int, startFuel: int, stations: List[List[int]]) -> int:
stations += [(target,0)]
# 刚开始有startFuel升汽油
cur = startFuel
ans = 0
# 最大堆
h = []
# 上一次的位置
last = 0
for i,fuel in stations:
# 当前有多少升汽油,i表示当前加油站的位置
cur -= i - last
# 如果cur<0并且h不为空,则说明必须加油
while cur < 0 and h:
# 在已经走过的位置中汽油最多的站中加油
cur -= heapq.heappop(h)
ans += 1
# 循环结束条件为cur>=0或者h为空,当cur<0时,说明h为空,到不了终点
if cur < 0:
return -1
# 构造大顶堆
heapq.heappush(h,-fuel)
# 更新位置
last = i
return ans
1642. 可以到达的最远建筑
给你一个整数数组
heights,表示建筑物的高度。另有一些砖块bricks和梯子ladders。
你从建筑物 0 开始旅程,不断向后面的建筑物移动,期间可能会用到砖块或梯子。
当从建筑物 i 移动到建筑物 i+1(下标 从 0 开始 )时:
- 如果当前建筑物的高度 大于或等于 下一建筑物的高度,则不需要梯子或砖块
- 如果当前建筑的高度 小于 下一个建筑的高度,您可以使用 一架梯子 或 (h[i+1] - h[i]) 个砖块
- 如果以最佳方式使用给定的梯子和砖块,返回你可以到达的最远建筑物的下标(下标 从 0 开始 )。
示例:
输入:heights = [4,2,7,6,9,14,12], bricks = 5, ladders = 1
输出:4
解释:从建筑物 0 出发,你可以按此方案完成旅程:
- 不使用砖块或梯子到达建筑物 1 ,因为 4 >= 2
- 使用 5 个砖块到达建筑物 2 。你必须使用砖块或梯子,因为 2 < 7
- 不使用砖块或梯子到达建筑物 3 ,因为 7 >= 6
- 使用唯一的梯子到达建筑物 4 。你必须使用砖块或梯子,因为 6 < 9无法越过建筑物 4 ,因为没有更多砖块或梯子。
思路:事后诸葛亮
先遍历一遍diff(要跨越的建筑物的高度差),然后构造大顶堆,等砖头不够时,我们就应该用梯子了,此时,将前面最大堆的堆顶元素替换成梯子,由于前面是用砖头造的,就相当于把梯子兑换成砖头了
class Solution:
def furthestBuilding(self, heights: List[int], bricks: int, ladders: int) -> int:
# 最大堆
h = []
for i in range(1,len(heights)):
diff = heights[i] - heights[i-1]
# 如果高度差小于等于0,则不需要梯子或砖块
if diff <= 0:
continue
# 如果砖块数小于高度差并且还有梯子时,就是用梯子
if bricks < diff and ladders > 0:
ladders -= 1
# 前面走过的最大高度差大于现在的,说明前面用砖头浪费了,应该用梯子,那就相当于兑换成砖头
if h and -h[0] > diff:
# 这种情况兑换成砖头
bricks -= heapq.heappop(h)
else:
continue
# 如果砖头数大于高度差,就用砖头
bricks -= diff
# 如果当前砖头数小于0,表明到不了当前建筑物,返回上一建筑物下标
if bricks < 0:
return i - 1
heapq.heappush(h,-diff)
return len(heights) - 1
如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论或者私信!
![]()


