2021-05-06
二维超声速流动的数值解——普朗特-迈耶稀疏波程序分享
本文主要分享了安德森的《计算流体力学基础及其应用》一书中:“二维超声速流动的数值解——普朗特-迈耶稀疏波” 的程序求解。水平有限,请见谅!
文章目录
- 二维超声速流动的数值解——普朗特-迈耶稀疏波程序分享
-
- Matlab
-
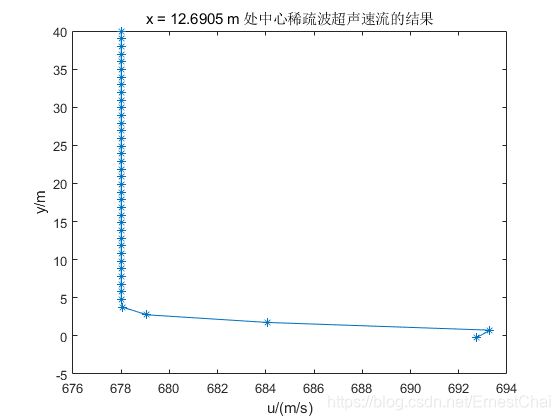
- x = 12.6905 m 处中心稀疏波超声速流的结果
- Prandtl_Meyer.m
- test_Prandtl_Meyer.m
- 额外说明
Matlab
x = 12.6905 m 处中心稀疏波超声速流的结果
Prandtl_Meyer.m
function [u_t, v_t, rho_t, p_t, T_t, Ma_t, Delta_xi] = Prandtl_Meyer(x, u, v, rho, p, Ma)
% [u_t, v_t, rho_t, p_t, T_t, Ma_t] = Prandtl_Meyer(x, u, v, rho, p)
% 二维超声速流动的数值解——普朗特-迈耶稀疏波;
% 由x处的流场参数计算 x + Delta_x 处的参数;
% 输入是(i,j)处的流场参数,输出是(i+1,j)处的流场参数;
% u、u_t —— x方向的速度;
% v、v_t —— y方向的速度;
% rho、rho_t —— 密度;
% p、p_t —— 压力;
% Ma、Ma_t —— 马赫数;
% Delta_xi —— 从(i+1,j)到(i+2,j)的推进步长 Delta_xi;
%% 各种常数;
gama = 1.4; % 比热比;
CFL = 0.5;% CFL常数;
R = 8.314;% 理想气体常数 [J/(mol*K)];
M = 0.029; %空气的摩尔质量 [kg/mol];
Rg= R / M; % 空气的气体常数 [J/(kg*K)];
Cy = 0.6; %人工粘性常数;
%% 计算域;
J = 41; % y方向的计算节点数;
theta = 5.352/180 * pi;% 转角大小;
E = 10;% 转角位置;
% 物理平面;
ys = @(x) 0*(x>=0 & x<=E) + (-(x - E)*tan(theta))*(x>=E);% 下边界的纵坐标;
% h —— 物理平面从下表面到上边界的距离;
h = @(x) 40 * (x>=0 & x<= 10) + (40 + (x - 10)*tan(theta))*(x>=10 & x<=45);
Delta_y = h(x)/(J - 1);
y = ys(x):Delta_y:40;
% 计算平面;
eta = @(x,y) (y - ys(x))/h(x);
eta_min = 0;
eta_max = 1;
Delta_eta = (eta_max - eta_min)/(J - 1);
%% 度量;
partial_eta_x = @(x,y) 0*(x>=0 & x<=E)...
+ ((1 - eta(x,y))*tan(theta)/h(x))*(x>=E);
%% 推进步长 Delta_xi;
% 计算马赫角 mu;
mu = asin(1 ./ Ma);
% 计算推进步长 Delta_xi;
tan_max = max(max(abs(tan(theta + mu))), max(abs(tan(theta - mu))));
Delta_xi = CFL * Delta_y / tan_max;
%% 计算解向量 F 和 向量 G;
F1 = rho.*u;
F2 = rho.*u.*u + p;
F3 = rho.*u.*v;
F4 = gama/(gama - 1)*p.*u + rho.*u.*(u.*u + v.*v)/2;
G1 = rho.*F3./F1;
G2 = F3;
G3 = rho.*(F3./F1).^2 + F2 - F1.^2./rho;
G4 = gama/(gama - 1)*(F2 - F1.^2./rho).*F3./F1...
+ rho/2.*F3./F1.*((F1./rho).^2 + (F3./F1).^2);
%% 预估步计算 (i , j) 处的partial_F;
% 向前差分;
partial_F1 = zeros(1,J);
partial_F2 = zeros(1,J);
partial_F3 = zeros(1,J);
partial_F4 = zeros(1,J);
for j = 2:J-1
partial_F1(j) = partial_eta_x(x,y(j))*(F1(j) - F1(j+1))/Delta_eta...
+ 1/h(x)*(G1(j) - G1(j+1))/Delta_eta;
partial_F2(j) = partial_eta_x(x,y(j))*(F2(j) - F2(j+1))/Delta_eta...
+ 1/h(x)*(G2(j) - G2(j+1))/Delta_eta;
partial_F3(j) = partial_eta_x(x,y(j))*(F3(j) - F3(j+1))/Delta_eta...
+ 1/h(x)*(G3(j) - G3(j+1))/Delta_eta;
partial_F4(j) = partial_eta_x(x,y(j))*(F4(j) - F4(j+1))/Delta_eta...
+ 1/h(x)*(G4(j) - G4(j+1))/Delta_eta;
end
%% 计算预估步的人工粘性 SF;
SF1 = zeros(1,J);
SF2 = zeros(1,J);
SF3 = zeros(1,J);
SF4 = zeros(1,J);
for j = 2 : J-1
SF1(j) = Cy*abs(p(j+1) - 2*p(j) + p(j-1))/(p(j+1) + 2*p(j) + p(j-1))...
* (F1(j+1) - 2*F1(j) + F1(j-1));
SF2(j) = Cy*abs(p(j+1) - 2*p(j) + p(j-1))/(p(j+1) + 2*p(j) + p(j-1))...
* (F2(j+1) - 2*F2(j) + F2(j-1));
SF3(j) = Cy*abs(p(j+1) - 2*p(j) + p(j-1))/(p(j+1) + 2*p(j) + p(j-1))...
* (F3(j+1) - 2*F3(j) + F3(j-1));
SF4(j) = Cy*abs(p(j+1) - 2*p(j) + p(j-1))/(p(j+1) + 2*p(j) + p(j-1))...
* (F4(j+1) - 2*F4(j) + F4(j-1));
end
%% (i+1 , j) 处的预估值;
bar_F1 = F1 + partial_F1 * Delta_xi + SF1;
bar_F2 = F2 + partial_F2 * Delta_xi + SF2;
bar_F3 = F3 + partial_F3 * Delta_xi + SF3;
bar_F4 = F4 + partial_F4 * Delta_xi + SF4;
%% 求原变量 rho的 (i+1 , j) 处预估值 bar_rho;
% A、B和C为中间变量;
bar_A = bar_F3.^2 ./ (2 * bar_F1) - bar_F4;
bar_B = gama/(gama - 1) * bar_F1 .* bar_F2;
bar_C = - (gama + 1)/(2*(gama-1)) * bar_F1 .^3;
bar_rho = (- bar_B + sqrt(bar_B.^2 - 4*bar_A.*bar_C)) ./ (2*bar_A);
%% 计算bar_p,用于计算校正步的人工粘性 bar_SF;
bar_u = bar_F1 ./ bar_rho;
bar_p = bar_F2 - bar_F1 .* bar_u;
%% 求G的 (i+1 , j) 处的预估值 bar_G;
bar_G1 = bar_rho .* bar_F3 ./ bar_F1;
bar_G2 = bar_F3;
bar_G3 = bar_rho .* (bar_F3 ./ bar_F1).^2 ...
+ bar_F2 - bar_F1.^2 ./ bar_rho;
bar_G4 = gama/(gama - 1)*(bar_F2 - bar_F1.^2 ./ bar_rho) .* bar_F3 ./ bar_F1...
+ bar_rho/2 .* bar_F3 ./ bar_F1 .* ((bar_F1./bar_rho).^2 + (bar_F3./bar_F1).^2);
%% 校正步计算 (i+1 , j) 处的 bar_partial_F;
% 向后差分;
bar_partial_F1 = zeros(1,J);
bar_partial_F2 = zeros(1,J);
bar_partial_F3 = zeros(1,J);
bar_partial_F4 = zeros(1,J);
for j = 2 : J-1
bar_partial_F1(j) = partial_eta_x(x,y(j))*(bar_F1(j-1) - bar_F1(j))/Delta_eta...
+ 1/h(x)*(bar_G1(j-1) - bar_G1(j))/Delta_eta;
bar_partial_F2(j) = partial_eta_x(x,y(j))*(bar_F2(j-1) - bar_F2(j))/Delta_eta...
+ 1/h(x)*(bar_G2(j-1) - bar_G2(j))/Delta_eta;
bar_partial_F3(j) = partial_eta_x(x,y(j))*(bar_F3(j-1) - bar_F3(j))/Delta_eta...
+ 1/h(x)*(bar_G3(j-1) - bar_G3(j))/Delta_eta;
bar_partial_F4(j) = partial_eta_x(x,y(j))*(bar_F4(j-1) - bar_F4(j))/Delta_eta...
+ 1/h(x)*(bar_G4(j-1) - bar_G4(j))/Delta_eta;
end
%% 校正步的bar_partial_F改为向前差分;
bar_partial_F1(1) = partial_eta_x(x,y(1))*(bar_F1(1) - bar_F1(2))/Delta_eta...
+ 1/h(x)*(bar_G1(1) - bar_G1(2))/Delta_eta;
bar_partial_F2(1) = partial_eta_x(x,y(1))*(bar_F2(1) - bar_F2(2))/Delta_eta...
+ 1/h(x)*(bar_G2(1) - bar_G2(2))/Delta_eta;
bar_partial_F3(1) = partial_eta_x(x,y(1))*(bar_F3(1) - bar_F3(2))/Delta_eta...
+ 1/h(x)*(bar_G3(1) - bar_G3(2))/Delta_eta;
bar_partial_F4(1) = partial_eta_x(x,y(1))*(bar_F4(1) - bar_F4(2))/Delta_eta...
+ 1/h(x)*(bar_G4(1) - bar_G4(2))/Delta_eta;
%% 求 (i , j) 和 (i+1 , j) 之间的平均导数;
bar_partial_F1_av = (partial_F1 + bar_partial_F1) / 2;
bar_partial_F2_av = (partial_F2 + bar_partial_F2) / 2;
bar_partial_F3_av = (partial_F3 + bar_partial_F3) / 2;
bar_partial_F4_av = (partial_F4 + bar_partial_F4) / 2;
%% 计算校正步的人工粘性 bar_SF;
bar_SF1 = zeros(1,J);
bar_SF2 = zeros(1,J);
bar_SF3 = zeros(1,J);
bar_SF4 = zeros(1,J);
for j = 2 : J-1
bar_SF1(j) = Cy*abs(bar_p(j+1) - 2*bar_p(j) + bar_p(j-1))/(bar_p(j+1) + 2*bar_p(j) + bar_p(j-1))...
* (bar_F1(j+1) - 2*bar_F1(j) + bar_F1(j-1));
bar_SF2(j) = Cy*abs(bar_p(j+1) - 2*bar_p(j) + bar_p(j-1))/(bar_p(j+1) + 2*bar_p(j) + bar_p(j-1))...
* (bar_F2(j+1) - 2*bar_F2(j) + bar_F2(j-1));
bar_SF3(j) = Cy*abs(bar_p(j+1) - 2*bar_p(j) + bar_p(j-1))/(bar_p(j+1) + 2*bar_p(j) + bar_p(j-1))...
* (bar_F3(j+1) - 2*bar_F3(j) + bar_F3(j-1));
bar_SF4(j) = Cy*abs(bar_p(j+1) - 2*bar_p(j) + bar_p(j-1))/(bar_p(j+1) + 2*bar_p(j) + bar_p(j-1))...
* (bar_F4(j+1) - 2*bar_F4(j) + bar_F4(j-1));
end
%% (i+1 , j) 处的校正值;
F1_t = F1 + bar_partial_F1_av * Delta_xi + bar_SF1;
F2_t = F2 + bar_partial_F2_av * Delta_xi + bar_SF2;
F3_t = F3 + bar_partial_F3_av * Delta_xi + bar_SF3;
F4_t = F4 + bar_partial_F4_av * Delta_xi + bar_SF4;
%% 边界条件:计算(i+1,41)上边界处的流场参数;
% 注:此处采用沿垂直方向线性外插的方式是不合适的,而应该从内部网格点沿特征线外插;
F1_t(J) = 2*F1_t(J-1) - F1_t(J-2);
F2_t(J) = 2*F2_t(J-1) - F2_t(J-2);
F3_t(J) = 2*F3_t(J-1) - F3_t(J-2);
F4_t(J) = 2*F4_t(J-1) - F4_t(J-2);
%% (i + 1, j)处的原变量计算;
% 中间变量 A、B 和 C 的计算;
A_t = F3_t.^2 ./ (2 * F1_t) - F4_t;
B_t = gama/(gama - 1) * F1_t .* F2_t;
C_t = -(gama + 1) / (2*(gama - 1)) * F1_t.^3;
% 原变量的计算;
rho_t = (-B_t + sqrt(B_t.^2 - 4*A_t.*C_t)) ./ (2*A_t);
u_t = F1_t ./ rho_t;
v_t = F3_t ./ F1_t;
p_t = F2_t - F1_t.*u_t;
T_t = p_t ./ (rho_t * Rg);
Ma_t = sqrt((u_t.^2 + v_t.^2) ./ (gama * Rg * T_t));
%% 边界条件:计算(i+1,1)下边界处的流场参数;
psi = atan(abs(v_t(1))/u_t(1));% 速度向量的夹角;
% 分为扩张前(x<=E)的壁面和扩张后(x>E)的壁面的计算;
phi = psi*(x<=E) + (theta - psi)*(x>E);
f_cal = sqrt((gama+1)/(gama-1))*atan(sqrt((gama-1)/(gama+1)*(Ma_t(1)^2-1)))...
- atan(sqrt(Ma_t(1)^2-1));
f_act = f_cal + phi; % 普朗特-迈耶关系式;
% 由f_act求解Ma_act;
Fun = @(Ma)sqrt((gama+1)/(gama-1))*atan(sqrt((gama-1)/(gama+1)*(Ma^2-1)))...
- atan(sqrt(Ma^2-1)) - f_act;
Ma_act = fsolve(Fun, 2.2);
% 计算真实的压力、密度与温度;
% Ma_t(1) 即 Ma_cal;
p_t(1) = p_t(1) * ((1 + ((gama-1)/2) * Ma_t(1)^2) / (1 + ((gama-1)/2) * Ma_act^2))^(gama/(gama-1));
T_t(1) = T_t(1) * ((1 + ((gama-1)/2) * Ma_t(1)^2) / (1 + ((gama-1)/2) * Ma_act^2));
rho_t(1) = p_t(1)/(Rg*T_t(1));
% 计算 y 方向的速度 v;
% u_t(1) = u_cal;
v_t(1) = 0 * (x<=E) + (- u_t(1) * tan(theta))*(x>E);
Ma_t(1) = Ma_act; % Ma-act才是真正的马赫数;
%% 从(i+1,j)到(i+2,j)的推进步长 Delta_xi;
% 计算马赫角 mu;
mu = asin(1 ./ Ma_t);
% 计算推进步长 Delta_xi;
tan_max = max(max(abs(tan(theta + mu))), max(abs(tan(theta - mu))));
Delta_xi = CFL * Delta_y / tan_max;
end
test_Prandtl_Meyer.m
% Author: CXT
% Date: 2021/5/6
% Theme: 二维超声速流动的数值解——普朗特-迈耶稀疏波;
clc;
clear;
close;
%% 初始条件(x = 0);
J = 41;
u = 678 * ones(1,J); % [m/s];
v = zeros(1,J);% [m/s];
rho = 1.23 * ones(1,J); % [kg/m3];
p = 0.101 * 10^6 * ones(1,J); % [N/m2];
T = 286 * ones(1,J); % [K]
Ma = 2 * ones(1,J); % [1];
%% test;
x = 0;
for i = 1:100
[u, v, rho, p, T, Ma, Delta_xi] = Prandtl_Meyer(x, u, v, rho, p, Ma);
x = x + Delta_xi;
if (x>=12.928)
break;
end
end
%% 绘图;
% 计算 x 所在的 y 的分布;
x = x - Delta_xi;
theta = 5.352/180 * pi;% 转角大小;
E = 10;% 转角位置;
ys = @(x) 0*(x>=0 & x<=E) + (-(x - E)*tan(theta))*(x>=E);% 下边界的纵坐标;
% h —— 物理平面从下表面到上边界的距离;
h = @(x) 40 * (x>=0 & x<= 10) + (40 + (x - 10)*tan(theta))*(x>=10 & x<=45);
Delta_y = h(x)/(J - 1);
y = ys(x):Delta_y:40;
figure;
plot(u,y,'*-');
xlabel('u/(m/s)');
ylabel('y/m');
title("x = 12.6905 m 处中心稀疏波超声速流的结果");
额外说明
在计算到 x = 45.0246 m 处,程序就爆掉了。错误提示信息如下:
索引超出数组元素的数目(0)。
出错 Prandtl_Meyer (第 70 行)
partial_F1(j) = partial_eta_x(x,y(j))*(F1(j) - F1(j+1))/Delta_eta...
出错 test_Prandtl_Meyer (第 20 行)
[u, v, rho, p, T, Ma, Delta_xi] = Prandtl_Meyer(x, u, v, rho, p, Ma);
笔者未找出原因,也未对该问题进行深究!