Python解答蓝桥杯省赛真题之从入门到真题(续)
由于上篇文章太长了导致MD编辑器很卡,所以另写了一篇接续
如有想看上篇文章的
传送门在此
Python解答蓝桥杯省赛真题之从入门到真题
二刷时发现之前的代码有运行不出来,已改正!
文章目录
- 1.真题篇
-
- 1.1 方格分割
- 1.2 迷宫
- 1.3 15.125GB
- 1.4. 约数个数
- 1.5. 叶结点数
- 1.6. 数字9
- 1.7. 数位递增的数
- 1.8. 递增三元组
- 1.9. 音节判断
- 1.10. 长草
- 1.11. 序列计数
- 1.12. 晚会节目单
- 1.13. 合根植物
- 1.14. 第几个幸运数
- 1.15. 乘积尾零
- 1.16. 全球变暖
1.真题篇
1.1 方格分割
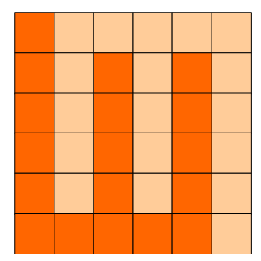
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
def dfs(x, y):
global ans
if x == 0 or x == n or y == 0 or y == n:
ans += 1
return
for i in range(4):
tx = x + directions[i][0]
ty = y + directions[i][1]
if arr_map[tx][ty] == 0:
arr_map[tx][ty] = 1
arr_map[n - tx][n - ty] = 1
dfs(tx, ty)
arr_map[tx][ty] = 0
arr_map[n - tx][n - ty] = 0
return ans / 4
n = 6
ans = 0
arr_map = [[0] * (n + 1) for i in range(10)]
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
arr_map[3][3] = 1
# print(arr_map)
if __name__ == '__main__':
print(dfs(n // 2, n // 2)) # 509
# print(ans)
"""
注释:
从中心带你(3,3)开始出发,两边对称走,最后总数要除以4
"""
1.2 迷宫
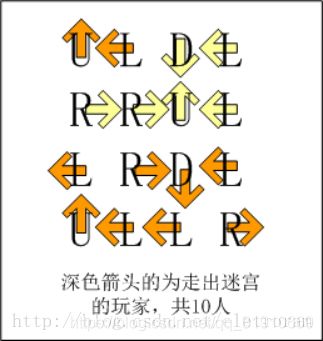
X星球的一处迷宫游乐场建在某个小山坡上。
它是由10x10相互连通的小房间组成的。
房间的地板上写着一个很大的字母。
我们假设玩家是面朝上坡的方向站立,则:
L表示走到左边的房间,
R表示走到右边的房间,
U表示走到上坡方向的房间,
D表示走到下坡方向的房间。
X星球的居民有点懒,不愿意费力思考。
他们更喜欢玩运气类的游戏。这个游戏也是如此!
开始的时候,直升机把100名玩家放入一个个小房间内。
玩家一定要按照地上的字母移动。
迷宫地图如下:
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR
请你计算一下,最后,有多少玩家会走出迷宫?
而不是在里边兜圈子。
请提交该整数,表示走出迷宫的玩家数目,不要填写任何多余的内容。
如果你还没明白游戏规则,可以参看一个简化的4x4迷宫的解说图:
最近忙于结课的小论文作业,都快忘记蓝桥杯的事情了,话说到底什么时候考试呢?
前边做过的题目几乎没有印象了快要,还是要多复习呀!
老话讲的好,温故而知新。
闲话不多说,这个问题主要还是dp问题,一个数组记录迷宫,一个数组记录走过的路
上代码
def dfs(x, y):
"""
深度搜索
:param x: 位置横坐标
:param y: 位置纵坐标
:return: None
"""
global ans
while True:
"""所在(x, y)位置的人按照标识走出迷宫后推出循环"""
# print(x, y)
if x > 9 or x < 0 or y > 9 or y < 0:
ans += 1
# print(ans)
break
if data_map[x][y] == 1:
break
# 记录走过的位置
data_map[x][y] = 1
if data[x][y] == 'U':
x -= 1
elif data[x][y] == 'D':
x += 1
elif data[x][y] == 'L':
# print(x, y)
y -= 1
elif data[x][y] == 'R':
y += 1
def get_num():
"""
获取走出迷宫的人数
:return: 走出迷宫的人数
"""
global data_map
global ans
for i in range(0, 10):
for j in range(0, 10):
"""对每个位置进行遍历,注意每次遍历开始前要先对data_map清0"""
# data_map = [[0] * 10] * 10 # 不要用这种方式定义,这样data_map[1][1] = 1 会导致每一行的第一个位置都为1
data_map = [[0] * 10 for _ in range(10)] # 这样行
# print(i, j)
dfs(i, j)
return ans
def get_data(file_name):
"""
获取数据
:param file_name: 保存数据的文件
:return: 获取的数据
"""
data = []
with open(file_name, mode='rt', encoding='utf-8') as f:
for line in f:
line = list(line.strip())
data.append(line)
return data
# data_map = [[0] * 10] * 10 # 不要用这种方式定义,这样data_map[1][1] = 1 会导致每一行的第一个位置都为1
data_map = [[0] * 10 for _ in range(10)] # 这样行
# data_map = [[0 for _ in range(10)] for i in range(10)] # 这样也行
# data_map = []
# for i in range(10):
# data_map.append([0 for i in range(10)])
data = get_data('maze2')
ans = 0
if __name__ == '__main__':
print(get_num()) # 31个人
# dfs(8, 2)
1.3 15.125GB
【问题描述】
在计算机存储中,15.125GB是多少MB?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
1KiB(Kilobyte)=1024B ,即2的10次方字节zd,读音“千字节”
1MiB(Megabyte)=1024KiB,即2的20次方字内节,读音“兆字节”
1GiB(Gigabyte)=1024MiB,即2的30次方字节,读音“吉字节”
1TiB(Terabyte)=1024GiB,即2的40次方字节容,读音“太字节”
1PiB(Petabyte)=1024TiB,即2的50次方字节,读音“拍字节”
1EiB(Exabyte) =1024PiB,即2的60次方字节,读音“艾字节”
1ZiB(Zettabyte)=1024EiB,即2的70次方字节,读音“Z字节”
1YiB(Yottabyte)=1024ZiB,即2的80次方字节,读音“Y字节
比特(bit)是最小的存储单位。
计算机存储单位一般用字节(Byte)、千字节(KB)、兆字节(MB)、吉字节(GB)、太字节(TB)、拍字节(PB)、艾字节(EB)、泽它字节(ZB,又称皆字节)、尧它字节(YB)表示。
capacity = 15.125 * 1024
print(capacity)
15488
1.4. 约数个数
【问题描述】
1200000有多少个约数(只计算正约数)。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
约数,又叫因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。在自然数(0和正整数)的范围内,任何正整数都是0的约数。4的正约数有:1、2、4。6的正约数有:1、2、3、6。10的正约数有:1、2、5、10。12的正约数有:1、2、3、41215的正约数有:1、3、5、15。18的正约数有:1、2、3、6、9、18。20的正约数有:1、2、4、5、10、20。注意:一个数的约数必然包括1及其本身。
count = 2 # 1 and itself
num = 1200000
for i in range(2, num): # From 2 to num - 1
if num % i == 0:
count += 1
# print(i, end=' ') # Show all divisors
print(count)
96
1.5. 叶结点数
【问题描述】
一棵包含有2019个结点的二叉树,最多包含多少个叶结点?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
最多叶子结点数就是求其对应的完全二叉树
然后求2019个结点的完全二叉树的叶子结点即可
def most_leaf_nodes(total):
layer = 0
while 2 ** layer - 1 < total:
layer += 1
now_layer = layer - 1
now_layer_nodes = 2 ** (layer - 2)
now_total_nodes = 2 ** (layer - 1) - 1
left_nodes = total - now_total_nodes
leaf_nodes = now_layer_nodes - (left_nodes // 2 + left_nodes % 2) + left_nodes
return leaf_nodes
print(most_leaf_nodes(2019))
1010
1.6. 数字9
【问题描述】
在1至2019中,有多少个数的数位中包含数字9?
注意,有的数中的数位中包含多个9,这个数只算一次。例如,1999这个数包含数字9,在计算只是算一个数。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
数位分离
def is_contains_9(num):
"""It's four, no need to cycle."""
one = num % 10
ten = num // 10 % 10
hundred = num // 100 % 10
thousand = num // 1000 % 10
if 9 in [one, ten, hundred, thousand]:
return True
else:
return False
ans = 0
given_number = 2019
for i in range(1, given_number + 1):
if is_contains_9(i):
# print(i, end=' ') # list all eligible numbers
ans += 1
print('\n', ans, sep='')
544
1.7. 数位递增的数
【问题描述】
一个正整数如果任何一个数位不大于右边相邻的数位,则称为一个数位递增的数,例如1135是一个数位递增的数,而1024不是一个数位递增的数。
给定正整数 n,请问在整数 1 至 n 中有多少个数位递增的数?
【输入格式】
输入的第一行包含一个整数 n。
【输出格式】
输出一行包含一个整数,表示答案。
【样例输入】
30
【样例输出】
26
【评测用例规模与约定】
对于 40% 的评测用例,1 <= n <= 1000。
对于 80% 的评测用例,1 <= n <= 100000。
对于所有评测用例,1 <= n <= 1000000。
dp动态规划
def dfs(pos, pre, limit):
if pos == -1: # 单独一位算一个
return 1
if not limit and dp[pos][pre] != -1: # 返回dp二维表中记录的值
return dp[pos][pre]
up = a[pos] if limit else 9
ans = 0
for i in range(pre, up + 1):
ans += dfs(pos - 1, i, limit and i == a[pos])
if not limit: # 把算过的值记录在dp二维表中
dp[pos][pre] = ans
return ans
def solve(num):
k = 0
while num != 0:
a[k] = num % 10
k += 1
num = num // 10
return dfs(k - 1, 0, True)
a = [0 for _ in range(10)]
dp = [[-1 for _ in range(10)] for _ in range(11)]
n = int(input())
print(solve(n) - 1)
# print(a, dp, sep='\n')
当输入1000时,数组中数据记录
1000
219
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
[[10, 9, 8, 7, 6, 5, 4, 3, 2, 1],
[55, 45, 36, 28, 21, 15, 10, 6, 3, 1],
[220, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1]]
1.8. 递增三元组
【问题描述】
在数列 a[1], a[2], …, a[n] 中,如果对于下标 i, j, k 满足 0
【输入格式】
输入的第一行包含一个整数 n。
第二行包含 n 个整数 a[1], a[2], …, a[n],相邻的整数间用空格分隔,表示给定的数列。
【输出格式】
输出一行包含一个整数,表示答案。
【样例输入】
5
1 2 5 3 5
【样例输出】
2
【样例说明】
a[2] 和 a[4] 可能是三元组的中心。
【评测用例规模与约定】
对于 50% 的评测用例,2 <= n <= 100,0 <= 数列中的数 <= 1000。
对于所有评测用例,2 <= n <= 1000,0 <= 数列中的数 <= 10000。
按顺序比大小,用过的中心入栈,之后就不能再用了
n = int(input())
arr = list(map(int, input().split()))
count = 0
data = []
for i in range(n):
for j in range(i + 1, n):
for k in range(j + 1, n):
if arr[i] < arr[j] < arr[k]:
if arr[j] not in data:
data.append(arr[j])
count += 1
# count += 1
# arr[j] = 0
print(count)
1.9. 音节判断
【问题描述】
小明对类似于 hello 这种单词非常感兴趣,这种单词可以正好分为四段,第一段由一个或多个辅音字母组成,第二段由一个或多个元音字母组成,第三段由一个或多个辅音字母组成,第四段由一个或多个元音字母组成。
给定一个单词,请判断这个单词是否也是这种单词,如果是请输出yes,否则请输出no。
元音字母包括 a, e, i, o, u,共五个,其他均为辅音字母。
【输入格式】
输入一行,包含一个单词,单词中只包含小写英文字母。
【输出格式】
输出答案,或者为yes,或者为no。
【样例输入】
lanqiao
【样例输出】
yes
【样例输入】
world
【样例输出】
no
【评测用例规模与约定】
对于所有评测用例,单词中的字母个数不超过100。
这里直接列出了 也可以自己编一个判断函数
word = input()
vowel = ['a', 'e', 'i', 'o', 'u']
i = 0
ans = 0
if word[i] in vowel:
print('no')
else:
ans += 1
i += 1
while i < len(word):
if word[i] not in vowel:
i += 1
else:
ans += 1
# print(ans, i)
break
while i < len(word):
if word[i] in vowel:
i += 1
else:
ans += 1
# print(ans, i)
break
while i < len(word):
if word[i] not in vowel:
i += 1
else:
ans += 1
# print(ans, i)
break
while i < len(word):
if word[i] in vowel:
i += 1
else:
ans += 1
break
if ans == 4:
print('yes')
else:
print('no')
1.10. 长草
【问题描述】
小明有一块空地,他将这块空地划分为 n 行 m 列的小块,每行和每列的长度都为 1。
小明选了其中的一些小块空地,种上了草,其他小块仍然保持是空地。
这些草长得很快,每个月,草都会向外长出一些,如果一个小块种了草,则它将向自己的上、下、左、右四小块空地扩展,这四小块空地都将变为有草的小块。
请告诉小明,k 个月后空地上哪些地方有草。
【输入格式】
输入的第一行包含两个整数 n, m。
接下来 n 行,每行包含 m 个字母,表示初始的空地状态,字母之间没有空格。如果为小数点,表示为空地,如果字母为 g,表示种了草。
接下来包含一个整数 k。
【输出格式】
输出 n 行,每行包含 m 个字母,表示 k 个月后空地的状态。如果为小数点,表示为空地,如果字母为 g,表示长了草。
【样例输入】
4 5
.g...
.....
..g..
.....
2
【样例输出】
gggg.
gggg.
ggggg
.ggg.
【评测用例规模与约定】
对于 30% 的评测用例,2 <= n, m <= 20。
对于 70% 的评测用例,2 <= n, m <= 100。
对于所有评测用例,2 <= n, m <= 1000,1 <= k <= 1000。
输出二位列表元素
for i in range(n):
print(*arr[i], sep=’’)
输出一维列表元素
print(*arr, sep=’’)
此处arr为一维数组
def grow_grass(x, y):
for q in range(4):
tx = x + next_[q][0]
ty = y + next_[q][1]
if tx >= 0 and tx < n and ty >= 0 and ty < m: # 不能越界
if arr[tx][ty] == '.': # 如果本来就有草,则不动,无草,才长
arr[tx][ty] = 'g'
flag[tx][ty] = 1
n, m = map(int, input().split())
arr = [list(input()) for _ in range(n)]
flag = [[0 for _ in range(m)] for _ in range(n)]
next_ = [[-1, 0], [1, 0], [0, -1], [0, 1]] # 用来表示(x, y)的上下左右四个位置
k = int(input())
# print(arr)
# exit()
for i in range(k):
flag = [[0 for _ in range(m)] for _ in range(n)]
for j in range(n):
for p in range(m):
if arr[j][p] == 'g' and flag[j][p] == 0:
# print(j, p)
flag[j][p] = 1
grow_grass(j, p)
for i in range(n):
print(*arr[i], sep='')
# print(arr)
# print(flag)
1.11. 序列计数
【问题描述】
小明想知道,满足以下条件的正整数序列的数量:
1. 第一项为 n;
2. 第二项不超过 n;
3. 从第三项开始,每一项小于前两项的差的绝对值。
请计算,对于给定的 n,有多少种满足条件的序列。
【输入格式】
输入一行包含一个整数 n。
【输出格式】
输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
【样例输入】
4
【样例输出】
7
【样例说明】
以下是满足条件的序列:
4 1
4 1 1
4 1 2
4 2
4 2 1
4 3
4 4
【评测用例规模与约定】
对于 20% 的评测用例,1 <= n <= 5;
对于 50% 的评测用例,1 <= n <= 10;
对于 80% 的评测用例,1 <= n <= 100;
对于所有评测用例,1 <= n <= 1000。
有难度
解释在代码注释中
def next_item(res):
res_ = []
size = len(res)
ab = abs(res[size - 1] - res[size - 2])
if ab <= 1:
return None
for i in range(1, ab):
new_res = []
new_res += res
new_res.append(i)
res_.append(new_res)
return res_
MOD = 10000
n = int(input())
res_list = []
temp_list = []
accept_list = []
for i in range(1, n + 1):
res = [n, i] # 两项时的情况
res_list.append(res) # 把所有两项情况加入res_list记录
temp_list += res_list # 把res_list记录进temp_list
while len(temp_list) > 0:
for i in range(len(temp_list)): # 判断temp_list的每一项
next_ = next_item(temp_list[i]) # 判断这项可以再派生下一项
# print(next_)
if next_ is not None: # 如果可以派生下一项,添加记录到accept_list
accept_list += next_
temp_list.clear() # 清空
if len(accept_list) != 0:
# print(accept_list)
# print(res_list)
res_list = accept_list + res_list # 把新派生出的项加到res_list,res_list此时已包含两项加新派生的项
# print(res_list)
temp_list += accept_list # 新派生的项加到temp_list进行下次循环用
accept_list.clear()
# print(res_list) # 循环结束后,此时所有满足条件的项都在res_list中
print(len(res_list) % MOD)
1.12. 晚会节目单
【问题描述】
小明要组织一台晚会,总共准备了 n 个节目。然后晚会的时间有限,他只能最终选择其中的 m 个节目。
这 n 个节目是按照小明设想的顺序给定的,顺序不能改变。
小明发现,观众对于晚上的喜欢程度与前几个节目的好看程度有非常大的关系,他希望选出的第一个节目尽可能好看,在此前提下希望第二个节目尽可能好看,依次类推。
小明给每个节目定义了一个好看值,请你帮助小明选择出 m 个节目,满足他的要求。
【输入格式】
输入的第一行包含两个整数 n, m ,表示节目的数量和要选择的数量。
第二行包含 n 个整数,依次为每个节目的好看值。
【输出格式】
输出一行包含 m 个整数,为选出的节目的好看值。
【样例输入】
5 3
3 1 2 5 4
【样例输出】
3 5 4
【样例说明】
选择了第1, 4, 5个节目。
【评测用例规模与约定】
对于 30% 的评测用例,1 <= n <= 20;
对于 60% 的评测用例,1 <= n <= 100;
对于所有评测用例,1 <= n <= 100000,0 <= 节目的好看值 <= 100000。
尽可能的好看,表示贪心
每次开始选的时候都要选可选择的值中的表示最好看的值
第一次选只能从前n - m 个中选择
之后则从选出的值对应的索引序号后开始到n - m + count中选
选出的值放入items列表中
当items列表长度小于n - m时开始循环
选满m个值后结束循环
提示:
输出列表直接元素,不带两侧的列表符号
print(*items)
下面这样输出的会带列表符号
print(items)
n, m = map(int, input().split())
count = 1
values = list(map(int, input().split()))
items = [max(values[:n - m + 1])]
max_i = values.index(items[0])
while len(items) < m:
items.append(max(values[max_i + 1:n-m+count+1]))
max_i = values.index(items[count])
count += 1
print(*items)
找了两组测试数据
Example 1:
8 5
1 2 3 5 7 8 10 9
5 7 8 9 10
Example 2:
9 4
1 2 8 5 7 6 3 9 4
8 7 9 4
1.13. 合根植物
问题描述
w星球的一个种植园,被分成 m * n 个小格子(东西方向m行,南北方向n列)。每个格子里种了一株合根植物。
这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
输入格式
第一行,两个整数m,n,用空格分开,表示格子的行数、列数(1
格子的编号一行一行,从上到下,从左到右编号。
比如:5 * 4 的小格子,编号:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
样例输入
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
样例说明:其合根情况参考下图(注意:6也是一个连通子集)
![]()
样例输出
5
找带头大哥- pre列表中存储的是每个节点的带头大哥,比如1的带头大哥是13,节点5的带头大哥也是节点13,则1和5都属于一个节点集
- 最终pre的值 pre:[0, 13, 3, 3, 8, 13, 6, 8, 8, 13, 13, 13, 13, 13, 13, 20, 13, 13, 13, 20, 20]
- 最终lst的值 lst:[0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1]
def init(n):
for i in range(1, n+1):
pre[i] = i
def find_pre(key):
"""找key的根,也就是找带头大哥"""
if pre[key] == key:
return key
else:
pre[key] = find_pre(pre[key]) # 如果当前节点不是根节点,就找当前节点的父节点的根节点。最后的到的根就是key的根
return pre[key]
def unite(x, y):
"""如果x和y不相连则连接它们,即x的根和y的根不同,则让一方从属于另一方"""
rootx = find_pre(x)
rooty = find_pre(y)
if rootx != rooty:
pre[rootx] = rooty
m, n = list(map(int, input().split()))
line = int(input())
ans = 0
lst = [0 for i in range(m*n+1)]
pre = [0 for i in range(m*n+1)] # 存放以索引值为节点序号的点的根节点
init(m*n) # 初始化每个节点的根节点都为它自己,即开始时都各不相连
for i in range(line):
x, y = list(map(int, input().split()))
unite(x, y) # 每输入两个有关联的节点,就让他们相连
for i in range(1, m*n+1):
lst[find_pre(i)] = 1 # 遍历每个节点,把她们对应的根节点的索引位置赋值1,比如节点1的老大是13,5的老大也是13,则他们属于1个节点集,操作和都只能将lst的13索引的地方赋值1
for i in range(1, m*n+1): # 等于1的个数就是最后的子集个数
if lst[i] == 1:
ans += 1
print(ans)
1.14. 第几个幸运数
"""
题目描述
到x星球旅行的游客都被发给一个整数,作为游客编号。
x星的国王有个怪癖,他只喜欢数字3,5和7。
国王规定,游客的编号如果只含有因子:3,5,7,就可以获得一份奖品。
前10个幸运数字是:3 5 7 9 15 21 25 27 35 45,因而第11个幸运数字是:49
小明领到了一个幸运数字 59084709587505。
去领奖的时候,人家要求他准确说出这是第几个幸运数字,否则领不到奖品。
请你帮小明计算一下,59084709587505是第几个幸运数字。
输出
输出一个整数表示答案
"""
# def is_lucky(num):
# while num != 1:
# for i in [3, 5, 7]:
# if num % i == 0:
# num = num // i
# break
# else:
# return False
#
# return True
#
#
# ans = 0
#
# for i in range(2, 59084709587505):
# if is_lucky(i):
# ans += 1
#
# print(ans)
# 生成法
MAX = 59084709587505
# MAX = 49
a = [3, 5, 7]
s = set()
tou = 1
while True:
for i in a:
t = tou * i
if t <= MAX:
s.add(t)
lst = sorted(s)
for i in lst:
if i > tou:
tou = i
break
if tou >= MAX:
break
# print(lst)
print(len(s)) # 1905
1.15. 乘积尾零
"""
如下的10行数据,每行有10个整数,请你求出它们的乘积的末尾有多少个零?
5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211
注意:需要提交的是一个整数,表示末尾零的个数。不要填写任何多余内容。
"""
# 只有2和5才能产生0,所以我们把每个数分解成2*5*x 最后记录2和5的个数,最少的那个数的个数就是结果
with open('../数据/num', mode='r', encoding='utf-8') as f:
c2 = c5 = 0
for line in f:
line = line.strip().split()
for i in line:
num1 = num2 = int(i)
while num1 % 2 == 0:
num1 = num1 // 2
c2 += 1
while num2 % 5 == 0:
num2 = num2 // 5
c5 += 1
print(min(c2, c5)) # 31
1.16. 全球变暖
"""
你有一张某海域NxN像素的照片,"."表示海洋、"#"表示陆地,如下所示:
.......
.##....
.##....
....##.
..####.
...###.
.......
其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有2座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....#..
.......
.......
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
【输入格式】
第一行包含一个整数N。 (1 <= N <= 1000)
以下N行N列代表一张海域照片。
照片保证第1行、第1列、第N行、第N列的像素都是海洋。
【输出格式】
一个整数表示答案
"""
def dfs(x, y):
if fig[x][y] == '.':
return
direction = [[-1, 0], [1, 0], [0, -1], [0, 1]]
for i in range(4):
tx = x + direction[i][0]
ty = y + direction[i][1]
if 0 <= tx < n and 0 <= ty <= n and vis[tx][ty] != 1:
if fig[tx][ty] == '.':
fig[x][y] = '.'
vis[x][y] = 1
return
n = int(input())
fig = [list(input()) for _ in range(n)]
vis = [[0] * n for i in range(n)]
ans = 0
for i in range(n):
for j in range(n):
dfs(i, j)
for line in fig:
for c in line:
if c == '#':
ans += 1
print(ans)