Java数据结构与算法解析(十三)——优先级队列

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。

在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue) 。

定义

优先级队列和通常的栈和队列一样，只不过里面的每一个元素都有一个”优先级”，在处理的时候，首先处理优先级最高的。如果两个元素具有相同的优先级，则按照他们插入到队列中的先后顺序处理。

优先级队列可以通过链表，数组，堆或者其他数据结构实现。

优先级队列的实现方式

数组

最简单的优先级队列可以通过有序或者无序数组来实现，当要获取最大值的时候，对数组进行查找返回即可。

无序数组实现
如果使用无序数组，那么每一次插入的时候，直接在数组末尾插入即可，时间复杂度为O(1)，但是如果要获取最大值，或者最小值返回的话，则需要进行查找，这时时间复杂度为O(n)。

要实现删除最大元素，可以添加一段类似于选择排序的内循环代码，将最大元素的和边界元素交换后删除它，和对栈的pop()方法的实现一样。同样也可以加入调整数组的代码来达到动态调整数组的目的。

有序数组实现
如果使用有序数组，那么每一次插入的时候，通过插入排序将元素放到正确的位置，时间复杂度为O(n)，但是如果要获取最大值的话，由于元阿苏已经有序，直接返回数组末尾的 元素即可，所以时间复杂度为O(1).

在insert方法中添加代码，将所有较大的元素向右边移动一格以使数组保持有序（和插入排序一样）。这样，最大的元素总会在数组的一边，删除最大元素，只需要像栈的pop()一样就可以了。。

所以采用普通的数组或者链表实现，无法使得插入和排序都达到比较好的时间复杂度。所以我们需要二叉堆(binary heap)来实现优先级队列

链表表示法

我们还可以使用基于链表的下压栈的代码作为基础，而后可以选择修改pop()来找到并返回最大元素，或是修改push()来保证所有元素的逆序并用pop()来删除并返回链表的首元素。

二叉堆

二叉堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。 有了这一性质，那么二叉堆上最大值就是根节点了。

二叉堆的表现形式：我们可以使用数组的索引来表示元素在二叉堆中的位置。

从二叉堆中，我们可以得出：

· 元素k的父节点所在的位置为[k/2]

· 元素k的子节点所在的位置为2k和2k+1

跟据以上规则，我们可以使用二维数组的索引来表示二叉堆。通过二叉堆，我们可以实现插入和删除最大值都达到O(nlogn)的时间复杂度。

对于堆来说，最大元素已经位于根节点，那么删除操作就是移除并返回根节点元素，这时候二叉堆就需要重新排列；当插入新的元素的时候，也需要重新排列二叉堆以满足二叉堆的定义。

从下至上的堆有序变化
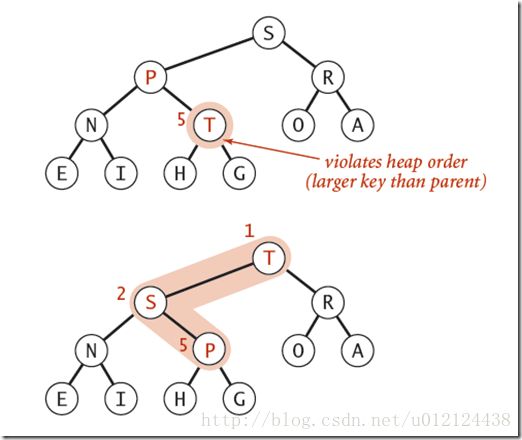
如果一个节点的值大于其父节点的值，那么该节点就需要上移，一直到满足该节点大于其两个子节点，而小于其根节点为止，从而达到使整个堆实现二叉堆的要求。

我们只需要将该元素k和其父元素k/2进行比较，如果比父元素大，则交换，然后迭代，一直到比父元素小为止。

private static void Swim(int k)
{
    //如果元素比其父元素大，则交换
    while (k > 1 && pq[k].CompareTo(pq[k / 2]) > 0)
    {
        Swap(pq, k, k / 2);
        k = k / 2;
    }
}

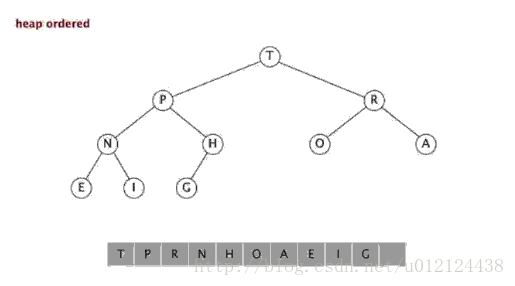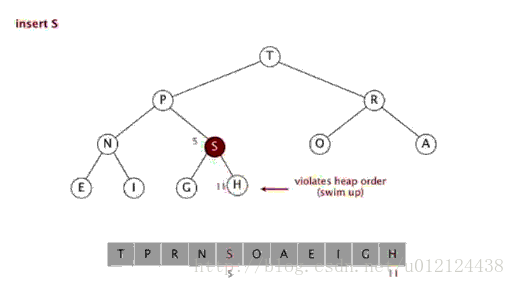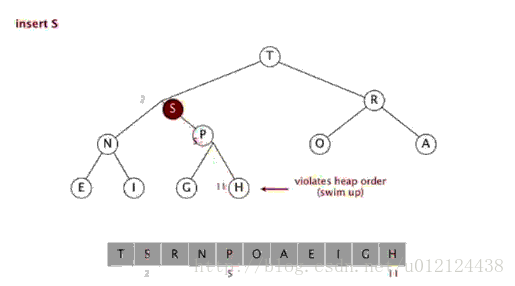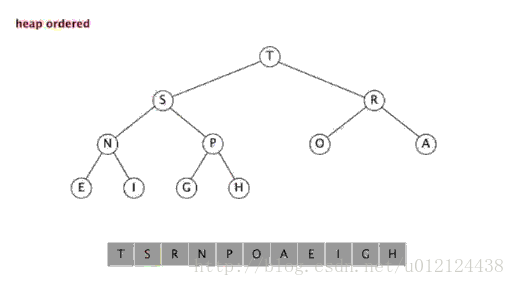
这样，往堆中插入新元素的操作变成了，将该元素从下往上重新建堆操作：

代码实现如下：

public static void Insert(T s)
{
    //将元素添加到数组末尾
    pq[++N] = s;
    //然后让该元素从下至上重建堆
    Swim(N);
}

由上至下的堆有序变化
当某一节点比其子节点要小的时候，就违反了二叉堆的定义，需要和其子节点进行交换以重新建堆，直到该节点都大于其子节点为止：

private static void Sink(int k)
{
    while (2 * k < N)
    {
        int j = 2 * k;
        //去左右子节点中，稍大的那个元素做比较
        if (pq[j].CompareTo(pq[j + 1]) < 0) j++;
        //如果父节点比这个较大的元素还大，表示满足要求，退出
        if (pq[k].CompareTo(pq[j]) > 0) break;
        //否则，与子节点进行交换
        Swap(pq, k, j);
        k = j;
    }
}

这样，移除并返回最大元素操作DelMax可以变为：

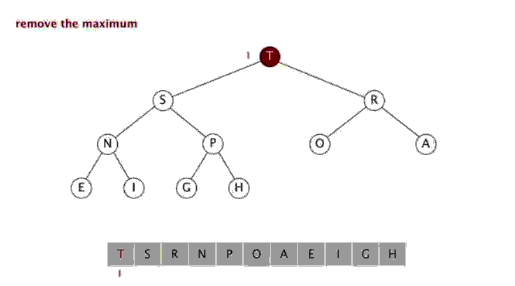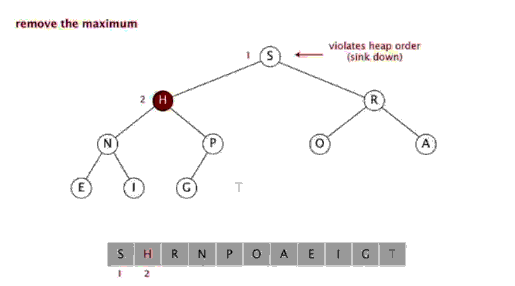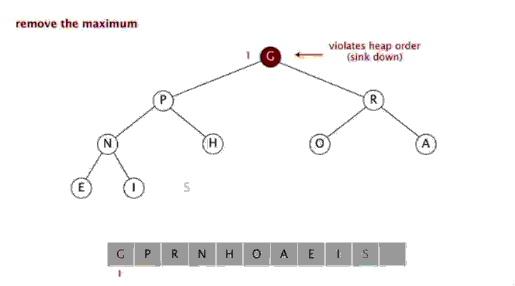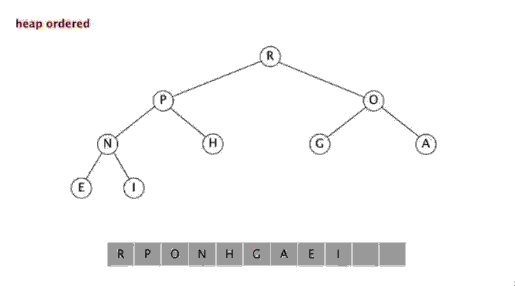
1. 移除二叉堆根节点元素，并返回

2. 将数组中最后一个元素放到根节点位置

3. 然后对新的根节点元素进行Sink操作，直到满足二叉堆要求。

移除最大值并返回的操作如下图所示：

public static T DelMax()
{
    //根元素从1开始，0不存放值
    T max = pq[1];
    //将最后一个元素和根节点元素进行交换
    Swap(pq, 1, N--);
    //对根节点从上至下重新建堆
    Sink(1);
    //将最后一个元素置为空
    pq[N + 1] = default(T);
    return max;
}

多叉堆

基于用数组表示的完全三叉树构造堆并修改相应的代码并不难，对应数组中1至N的N个元素，位置k的结点大于大于等于3k-1,3k，3k+1的结点，小于位于[(k+1)/3]下取整的结点。

d叉堆

完全d叉树，根最小。存储时使用层序。

操作跟二叉堆基本一致：insert,deleteMin,增大元素，减小元素，删除非顶元素，merge。

二叉堆与d叉堆的对比：