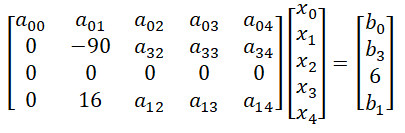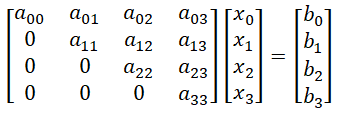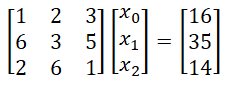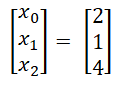夜深人静写算法（十六）- 高斯消元

一、算法概述

1、算法简述

a、线性方程组

• 高斯消元，一般用于求解线性方程组 AX = B（或 模线性方程组AX mod P = B）的问题，以 5 个未知数，4 个方程为例，AX = B表示成 4x5 的矩阵和 5x1 的矩阵（列向量）相乘的形式：
  
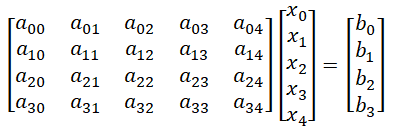
• 其中 A 和 B (b₀ b₁ b₂ b₃) 已知，需要求的是列向量 X(x₀ x₁ x₂ x₃ x₄) 的值。
• 消元中的元就会未知数，也就是逐步消去未知数的意思；

b、系数矩阵

• 这里的矩阵 A 称为系数矩阵；

c、增广矩阵

• 增广矩阵（又称扩增矩阵）就是在系数矩阵的右边添上一列，这一列是线性方程组的等号右边的值；

2、算法原理

• 1）方程组中任意两个方程交换位置，方程组等式关系仍然成立；
• 2）方程组中一个方程减去另一个方程，得到的方程等式关系仍然成立；
• 3）方程组中一个方程减去另一个方程的倍数，得到的方程等式关系仍然成立；
• 4）基于以上3点，可以将方程组转换成上三角的形式，如图所示：
  
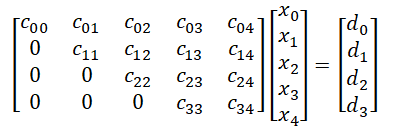
• 5）通过未知数少的等式（最下面的等式）将未知数的值确定，从而逐步回归，求解剩余未知数的值；
  
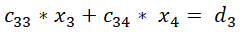
• 例如，以上等式中，有 2 种情况：
• • i）无解：c₃₃ 等于 0， c₃₄ 等于 0，d₃ 不等于 0；
• • ii）无穷多解：c₃₃ 不等于 0 或 c₃₄ 不等于 0 或 d₃ 等于 0；（情况 i 的取反）
• 6）求出最后一个等式的解以后，代入上一个等式，用同样的方式逐步减少未知数，最后求解所有未知数；

二、算法实现

• 对于n个方程，m个未知数的方程组，初始化当前处理列变量 col 为 0，消元的具体步骤如下：

1、初等行变换

a、选举交换

• 枚举所有的行，当枚举到第 i (0 <= i < n) 行时，每次从 [i, n) 行中找到第 col 列中元素绝对值最大的行和第 i 行进行交换；
  
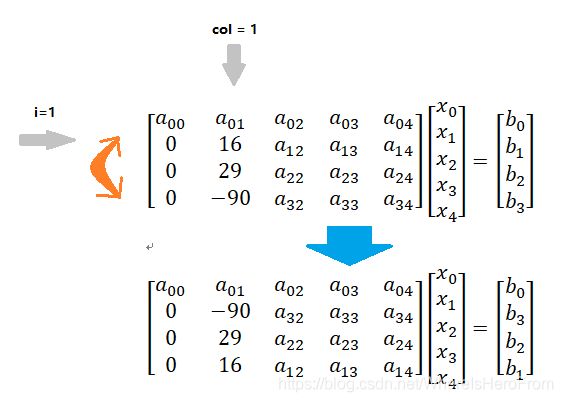
• 上图代表的是第1行和第3行进行交换的过程（注意：等式右边的 b 也要一起交换）；

b、全零跳过

• 如果找到的第 col 列绝对值最大的为 0 ，放弃这一列的处理，col + 1，i 不变，转 a、选举交换；

c、非零消零

• 如果绝对值最大的非 0，那么对于所有的行 j (i < j < n)，如果 a[j][col] 不为0，则需要进行消元，以期第 i 行以下的第 col 列的所有元素都消为0，具体步骤就是将第 j 行的所有元素减去第 i 行的所有元素乘上一个系数，这个系数即 a[j][col] / a[i][col] ）。
  

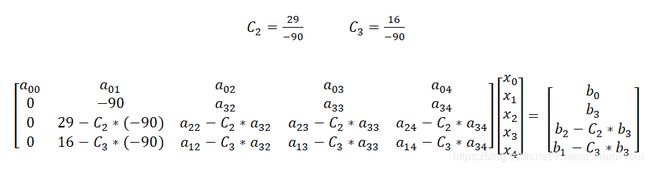
2、迭代消元

• 重复迭代进行初等行变换和消元，直到 n 个方程枚举完毕，或者当前列 col 等于 m；

3、解回归

a、无解

• 如果出现某一行，系数矩阵对应行全为0，增广矩阵对应行不全为0，则无解，如下图所示；
  

b、唯一解

• 如果是严格上三角，则表明有唯一解，如下图所示；
  

c、多解

• 如果增广矩阵有k (k > 0)行全为0，那么表明有k个变量可以任意取值，这几个变量即自由变量；对于这种情况，一般解的范围是给定的，令解的取值有T个，自由变量有V个，那么解的个数就是 TV （这里 T 也可能是无限的）；

4、算法举例

• 用高斯消元求一个 3 个未知数，3 个方程的解，如下：
  
• 1、初始增广矩阵（统一显示三位小数）

-	-	-	-
1.000	2.000	3.000	16.000
6.000	3.000	5.000	35.000
2.000	6.000	1.000	14.000

• 2、第 0 行 和 第 1 行 交换；

-	-	-	-
6.000	3.000	5.000	35.000
1.000	2.000	3.000	16.000
2.000	6.000	1.000	14.000

• 3、第 1、2 行进行消元，使得第 0 列元素从第 1 行开始均为 0 ；

-	-	-	-
6.000	3.000	5.000	35.000
0.000	1.500	2.167	10.167
0.000	5.000	-0.667	2.333

• 4、第 1 行 和 第 2 行 交换；

-	-	-	-
6.000	3.000	5.000	35.000
0.000	5.000	-0.667	2.333
0.000	1.500	2.167	10.167

• 5、第 2 行进行消元，使得第 1 列元素从第 2 行开始均为 0 ；

-	-	-	-
6.000	3.000	5.000	35.000
0.000	5.000	-0.667	2.333
0.000	0.000	2.367	9.467

• 6、从第2行开始回归，最终求得解如下：
  

三、算法时间复杂度分析

• 第一层循环枚举行 i ；
• 第二层循环第 j 和 减去 第 i 行的倍数；
• 第三层循环 第 j 行的每一列；
• 所以总是算法时间复杂度为 O(n³)；

四、问题类型

1、浮点数消元

• 系数矩阵为整数或浮点数，消元的时候乘上的系数为浮点数，一般用于求解浮点数解，例如HDU 3359；

2、整数消元

• 系数矩阵全为整数，消元的时候乘上的系数均为整数，整个消元过程不出现浮点数。由于乘法很容易溢出，一般很少用；

3、模线性方程组消元

• 系数矩阵全为整数，消元的时候乘上的系数均为整数，每次运算都模上一个数P，整个消元过程不出现除法，最后求解的时候用线性同余迭代求解，一般题型较多，有的是给定解的范围，求解的数量，例如：PKU 1830、HDU 3364；有的是求一个解，例如PKU 2065、HDU 3571；有的是求解的存在性，例如PKU1288、PKU 3185；
• 模板：高斯消元模板

五、经典题解析

来看几道经典的高斯消元，熟悉各种类型的高斯消元。

HDU 3359 Kind of a Blur

• 题意：H * W (W,H <= 10) 的矩阵A的某个元素A[i][j]，从它出发到其他点的曼哈顿距离小于等于D的所有值的和S[i][j]除上可达点的数目，构成了矩阵B。给定矩阵B，求矩阵A。

• 题解：将所有矩阵A的元素看成自变量，一共有 H * W 个变量，每个矩阵B的元素是由这些变量组合而成的，对于固定的B[i][j]，曼哈顿距离在D以内的A[x][y]的系数为1，其它为0，这样就变成了求 H * W 个变量和 H * W 个方程的线性方程组，高斯消元求解。这题数据量比较小，所以直接采用浮点数的高斯消元即可，需要注意的是，浮点数消元的时候为了避免精度误差，每次找最大的行，乘上一个小于1的系数进行消元，这样可以把误差降到最小。

PKU 1830 开关问题

• 题意：给定N(N < 29)个开关，每个开关打开和关闭的时候会引起另外一个开关的变化，本来为打开的会变成关闭，本来关闭的会变成打开。给定N个开关的初始状态和终止状态，以及关联的开关关系，求共有多少种方案从初始状态变成终止状态（不计顺序，并且每个开关只能操作至多一次）。
• 题解：由于开关只有打开和关闭两种状态，所以对于每个开关的打开和关闭，组合一下总共有2^N种情况，枚举所有情况判可行性，对于这个数据量来说是不现实的，需要想办法优化。
• 我们用X[i]来表示第i个开关的操作状态（1表示操作，0表示不操作）。
• 第 i 个开关会被哪些开关影响是可以知道的（这个关系在输入的时候会给出），假设影响第i个开关的开关列表为L[i][0], L[i][1], L[i][2]… 第i个开关的起始状态为S[i]，终止状态为E[i]，则可以列出N个方程：

( X[0] * A[i][0]  +  X[1] * A[i][1]  + ... +  X[n-1] * A[i][n-1]  ) % 2  =  (E[i] - S[i]);

• 每个方程代表一个开关被它本身以及它的关联开关操作后的最终状态，系数矩阵A[i][j]代表了开关之间的连带关系:
• 1. 如果第j个开关的操作能够影响第i个开关的状态，那么A[i][j] = 1;
• 2. 如果第j个开关的操作不影响第i个开关的状态，那么A[i][j] = 0;
• 3. 特殊的A[i][i] = 1(开关本身的操作必然会影响自己的当前状态);
• X[i]取值为0或1，这样就是N个N元一次方程组，利用高斯消元求解即可。将增广矩阵化简为上三角的形式后，剩余全为0的行的个数为自由变元的个数F（自由变元就是它在取值范围内可以取任意值，这题是个方阵，所以自由变元的个数等于全为0的行的个数），所以，由于开关一共两种状态，取值为0和1，所以总的解的个数为2^F。特殊的，如果某一行系数全为零，而增广矩阵最后一列对应行的值不为0，则表示无解。

HDU 3364 Lanterns

• PKU 1830的简单变种。那题是用开关来控制开关，这题是用开关来控制灯，而且开关和灯的数目是不一样的，这样就导致了高斯矩阵并不是一个方阵，而是一个N*M的矩阵，同样的构造系数矩阵的方法，当N和M不相等的情况下，自由变元的个数就不是剩余全为0的行的个数了。其实对于一般的方程，自由变元的个数为 Free =（变量数var - 非0系数向量的个数）。这题数据量比那题大，最大情况有可能是2^N，所以需要用__int64。

PKU 2065 SETI

• 题意：

• (a1 * 1⁰ + a2 * 1¹ + … an * 1ⁿ) % P = C1

• (a1 * 2⁰ + a2 * 2¹ + … an * 2ⁿ) % P = C2

• (a1 * 3⁰ + a2 * 3¹ + … an * 3ⁿ) % P = C3
  …

• (a1 * n⁰ + a2 * n¹ + … an * nⁿ) % P = Cn

• 给定n个以上的方程组，求满足条件的 ai (1 <= i <= n)。

• 题解：如果没有模 P，那么这个就是N个N元一次方程组，利用高斯消元可以求解，加上模P剩余后，其实原理一样，只不过在初等行变换后，每次进行消元的时候将所有值模P，最后求解回带的时候利用扩展欧几里得来对每一个ai求一个最小的可行解。

• 例如，最后化简的行阶梯阵如下图：
  

• 那么从后往前进行迭代求解的时候，必然会遇到两个数相乘模P等于一个常数的情况，比如求a4的时候，有同余数方程 3 * a4 % P = t4，可以表示成 3 * a4 + K * P = t4，其中P必然和3互素（题中有说明），所以这个方程必然有解，利用扩展欧几里得可以求得一个最小的非负整数a4，a4求出后同理求出a3、a2、a1即可。

PKU 3185 The Water Bowls

• 题意：20个开关排成一排，两边的开关的开启和关闭状态会带动相邻的一个开关，中间的开关的开启和关闭会带动相邻的两个开关，问给定一个状态能否将这些开关的状态都变为打开状态，如果能输出最小的操作次数。

• 题解：PKU 1830的变种，求最小的操作次数就是求所有解集中解的总和最小的解集，所以在进行初等行变换之后，利用dfs来枚举所有的解，当然如果不是自由变元的，解是确定的，由于开关开两次和不操作是一样的，所以每个开关的解集为{0, 1}，枚举过程中记录当前操作的次数，如果比之前记录的最小操作次数大，那么无须往下枚举，直接返回，作为剪枝。由于状态最多220种，加上适当的剪枝，可以很快把解搜出来。

HDU 3571 N-dimensional Sphere

• 题意：在一个N维空间中，给定一个N+1个点，求一个点使得它到所有点的距离都为R（R不给出），保证解为整数，并且解的范围为 [-10¹⁷, 10¹⁷]。

• 题解：对于N个未知数，N+1个方程，相邻两个方程相减可以把二次项全部约去，剩下一次项系数，则问题转化为N个未知数，N个方程的一次方程组，可以利用高斯消元求解，但是这题的数据量比较大，最大的可能解为1017，如果利用大数，乘法的复杂度很高，可以采用同余的方法，所以所有加法、减法、乘法需要模一个大的素数（需要大于10¹⁷的素数，可以利用拉宾米勒算法随机生成一个大素数P），然后利用同余方程求一个最小的非负数解，在进行相乘运算的时候最大情况会超过int64，所以处理乘法运算的时候需要用到二分加法，所有的乘模运算需要化简成加法和减法运算。利用 PKU 2065 的求法可以求得所有可行解，由于这题的数据量可能为负数，同余的情况下求出来的是非负数，为了消除这种情况，对所有输入的值加上一个偏移量10¹⁷，最后的解再减去这个偏移量，注意最后的答案减去偏移量的时候不需要取模（否则就没有意义了）。

SGU 173 Coins

• 题意：N(2 <= N <= 50)个硬币排成一排，有的人头朝上(用0表示)，有的则是字朝上(用1表示)，对这一排硬币进行M(1 <= M <= 10)次X变换之后的状态已知，求初始的硬币状态。

• 定义一次X变换如下：

• 1、从这一排硬币的Si(1 <= Si <= N, 1<= i <= M)位置取连续的K(2 <= K <= N)个硬币；

• 2、对这取出来的K个硬币进行一次循环左移操作；

• 3、扫描前K-1个硬币，如果第i个硬币字朝上(即为1)，并且Ai等于1，那么将第K个硬币进行一次翻转；

• 4、重复2) - 3) 操作Di(Di <= 106)次；

• 上述X变换的 3) 中出现了Ai，但是题目并未给出Ai ( 1 <= i <= K-1)，而是给出了L(L <= 200)个X变换之前的状态和之后的状态(每个状态为K个硬币)，需要利用这L条关系来求出Ai，并且题目保证Ai有且仅有一个解。

• 题解：题目兜兜转转绕了一大圈，实在很难读懂，只能通过样例来琢磨意思。这个题目分为两部分，首先是要把Ai求出来，然后再根据Ai的值和结束状态反推初始状态。

• 首先来看样例，L = 2, K = 3 两组X变换的前后状态为010 -> 101、101 -> 011。

• 对于第一对状态，010循环左移后为100，第K个硬币和结束状态不相符，说明前2(即K - 1)个硬币中字朝上的硬币对应的Ai必定有奇数个为1（这样才能使第K个硬币从0翻转到1），而前二个硬币只有第一个为1，所以A1 = 1;同理对于第二个状态，可以求出A2 = 0;

• 模拟一下样例可以大致了解题目的用意，但是对于一般的情况还是需要用系统的方法去分析，让我们来看下一般的情况，对于某一对状态如下：

初始状态S = S1 S2 S3...SK-1 SK                  
结束状态T = T1 T2 T3...TK-1 TK

• 将初始状态循环左移一次后为S’ = S2S3…SK-1SKS1，由于循环左移之后前K-1个硬币的状态不会再发生改变，所以有 S2S3…SK-1SK == T1T2T3…TK-1，当然这一点，题目数据是会保证的，我们不需要关心，我们需要关心的就是S1和TK 是否相等，如果S1和TK 相等，那么前T1T2T3…TK-1 中为1的对应的Ai=1的个数为偶数个，否则为奇数个。利用更加通俗的解释，即(T1 A1 + T2 A2 + T3A3 + …+ TK-1AK-1) mod 2 = S1 ^ TK，这个方程中，只有Ai是未知数，那么对于L个条件，我们可以列出L条方程，这样就转变成了L个方程K-1个未知数的模线性方程组，可以利用高斯消元求解Ai。
• Ai求出来后，给定一个结束状态，模拟M * Di次逆向操作，每次操作需要进行字符串的右移(因为是逆向，所以要和题目的左移相反)操作，每次右移最多牵涉N次原子操作，所以总的复杂度为O(NMDi)，复杂度过大，但是注意到这里的N <= 50，所以我们可以将每个状态压缩到一个int64的整数中，A1A2A3…AK-1也可以压缩成一个int64的整数，右移操作可以通过位运算在O(1)的时间内解决。其中有一步会涉及到判断一个数的二进制表示中有多少个1的问题，网上各种面试题很多，不再累述，比较方便、效率也还可以的是采用树状数组中lowbit的思想，即利用 x 减去 (x&(-x)) (其中 x&(-x) = 2^k， k为x二进制末尾0的个数），逐个将1消去，直到x = 0为止，迭代消去的次数就是1的个数。