夜深人静写算法(六)- RMQ
文章目录
- 一、前言
- 二、RMQ 简介和实现
-
- 1、RMQ 简介
- 2、RMQ 朴素算法
- 3、RMQ 的 ST 算法
-
- 1)算法思想
- 2)预处理
- 3)询问
- 4、RMQ 的 二维的扩展
- 三、RMQ 的应用与扩展
-
- 1、离散化
- 2、逆序数问题
- 3、区间 GCD
- 4、二分枚举配合RMQ
- 5、最长连续不重复子串
- 四、RMQ 题集整理
一、前言
学习算法的时候,切忌心浮气躁,就像十年前的我,为了竞赛取得成绩,恨不得把所有算法都啃了,结果大部分算法最后都没有吃透,只是学了个皮毛,真正遇到问题的时候,脑子没有转过弯来,就很难把算法和实际问题的关系联系起来。
原因还是因为学的时候太过功利,只是为了眼前的成败得失,而忽略了更加重要的东西。
更加重要的东西并不是这个算法本身,而是设计算法的思维以及思考的过程,算法是死的,思维是活的!今天要介绍的这个算法,利用了动态规划的思想,可谓经典中的经典,希望读者在看完我的这篇文章后,也能够和我一样引起共鸣,为前人的思考点赞!
那么,让我们开始吧!为了共同的愿景而努力!让天下没有难学的算法!
二、RMQ 简介和实现
1、RMQ 简介
- RMQ (Range Minimum / Maximum Query) 问题是指:对于长度为 n n n 的数列 A A A,回答若干询问 ( A , i , j ) ( 1 < = i , j < = n ) (A, i, j) (1 <= i,j <= n) (A,i,j)(1<=i,j<=n),返回数列 A A A 中区间在 [ i , j ] [i,j] [i,j] 中的最小 (大) 值所在的下标。也就是说, R M Q RMQ RMQ 问题是指求区间最值的问题。
- R M Q RMQ RMQ 总体来说还是动态规划的思想,相对比较独立的算法,不需要太深的程序和算法基础,而且相对好理解,所以放在了这一章来讲。
2、RMQ 朴素算法
- 以区间最小值为例,对于区间 [ l , r ] [l, r] [l,r],从第 l l l 个元素枚举到第 r r r 个元素,将值最小的元素的下标存储在变量 i d x idx idx 上,一旦遇到比记录的元素小的就更新 i d x idx idx 的值,枚举完所有 r − l + 1 r-l+1 r−l+1 个元素后,得到最小值所在的下标。
- C++代码实现如下:
int QueryMinIndex(int l, int r) {
int idx = l;
for(int i = l + 1; i <= r; ++i) {
if(A[i] < A[idx]) {
idx = i;
}
}
return idx;
}
- 我们发现这个算法的时间复杂度,最坏情况下就是 l = 1 , r = n l = 1,r = n l=1,r=n 的情况,为 O ( n ) O(n) O(n)。
- 当询问比较频繁的时候,这个算法的时间复杂度是无法满足要求的。
3、RMQ 的 ST 算法
1)算法思想
-
ST(Sparse Table)算法是基于动态规划的,之前在说到动态规划的时候,有个很重要的概念就是状态。
-
求解区间最大值可以通过所有数字增加一个负号转化成求区间最小值问题,所以这里我们可以只讨论区间最小值问题。
-
这个算法也利用到了状态的概念,用 f [ i ] [ j ] f[i][j] f[i][j] 表示起点为 j j j,长度为 2 i 2^i 2i 的区间内的最大值所在下标。通俗的讲, f [ i ] [ j ] f[i][j] f[i][j] 就是区间 [ j , j + 2 i ) [j, j + 2^i) [j,j+2i) 内的最大值的下标(注意:这里表示的区间为左闭右开)。
-
如图二-3-1所示,对于长度为 16 的数组, f [ i ] [ j ] f[i][j] f[i][j] 所表示的区间如下:

图二-3-1 -
由于区间 [ j , j + 2 i ) [j, j + 2^i) [j,j+2i) 长度为 2 i 2^i 2i,如果 i > 0 i > 0 i>0,那么它可以分解成两个长度为 2 i − 1 2^{i-1} 2i−1 的区间,即:
[ j , j + 2 i ) = [ j , j + 2 i − 1 ) + [ j + 2 i − 1 , j + 2 i ) [j, j + 2^i) = [j, j + 2^{i-1}) + [j + 2^{i-1}, j + 2^i) [j,j+2i)=[j,j+2i−1)+[j+2i−1,j+2i) -
当 i = 3 , j = 4 i=3, j = 4 i=3,j=4 时,有 [ 4 , 12 ) = [ 4 , 8 ) + [ 8 , 12 ) [4, 12) = [4,8) + [8,12) [4,12)=[4,8)+[8,12),更加直观的,如图二-3-2所示:

图二-3-2 -
由 图二-3-2 可知,父区间的最小值一定来自两个子区间中最小值的小者,对于数组 A A A,我们提供一个函数
RMQ_MinIndex(A[], l, r),函数传入两个下标,返回的是 A A A 数组中值较小的那个数的下标; -
C++ 代码实现如下:
int RMQ_MinIndex(ValueType A[], int l, int r) {
return A[r] < A[l] ? r : l;
}
- 这个函数在传参时需要保证 l < = r l <= r l<=r,并且由于数组长度并不一定是 2 的幂,所以 r r r 有可能超出数组长度,所以调用方需要进行边界判断;
- 通过这个函数,可以得到 f [ i ] [ j ] f[i][j] f[i][j] 的状态转移方程如下:
f [ i ] [ j ] = { j i = 0 o p t ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j + 2 i − 1 ] ) i > 0 f[i][j] = \begin{cases} j & i=0\\ opt(f[i-1][j], f[i-1][j + 2^{i-1}]) & i>0 \end{cases} f[i][j]={ jopt(f[i−1][j],f[i−1][j+2i−1])i=0i>0 - 其中 o p t opt opt 就是
RMQ_MinIndex函数;
2)预处理
- 给出数组 A A A,我们可以通过这个状态转移方程,进行两层循环预处理将 f [ i ] [ j ] f[i][j] f[i][j] 的值求出来;
- C++代码实现如下:
const int MAXM = 18;
const int MAXN = (1<<MAXM)+1;
void RMQ_Init(ValueType A[], int ALen, int(*f)[MAXN]) {
for (int i = 0; i < MAXM; i++) {
for (int j = 1; j + (1 << i) - 1 <= ALen; j++) {
if (i == 0) {
f[i][j] = j;
}
else {
f[i][j] = RMQ_MinIndex(A, f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);
}
}
}
}
- f [ i ] [ j ] f[i][j] f[i][j] 的状态数目有多少呢?
- 由于 i < = l o g ( n ) , j < = n i <= log(n), j <= n i<=log(n),j<=n,所以总的状态数为 n l o g ( n ) nlog(n) nlog(n),每次状态转移的时间复杂度为 O ( 1 ) O(1) O(1),所以预处理总时间为 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n))。
3)询问
- f [ i ] [ j ] f[i][j] f[i][j] 的计算只是做了一步预处理,但是我们在询问的时候,不能保证每个询问区间长度都是 2 的幂,如何利用预处理出来的值计算任何长度区间的值就是我们接下来要解决的问题。
- 区间长度等于 1 的情况最小值就等于它本身;
- 区间长度大于 1 时,即给定任意区间 [ a , b ] ( 1 < = a < b < = n ) [a, b] (1 <= a < b <= n) [a,b](1<=a<b<=n),必定可以找到两个区间 X 和 Y,它们的并是 [ a , b ] [a, b] [a,b],并且区间 X X X 的左端点是 a a a,区间 Y Y Y 的右端点是 b b b,而且两个区间长度相等,且都是 2 的幂,如图二-3-3所示:

- 设区间长度为 2 k 2^k 2k,则 X X X 表示的区间为 [ a , a + 2 k ) [a, a + 2^k) [a,a+2k), Y Y Y 表示的区间为 ( b − 2 k , b ] (b - 2^k, b] (b−2k,b],则需要满足一个条件就是 X X X 的右端点必须大于等于 Y Y Y 的左端点减一,即 a + 2 k − 1 > = b − 2 k a+2^k-1 >= b-2^k a+2k−1>=b−2k,通过移项得到:
2 k + 1 > = ( b − a + 1 ) 2^{k+1} >= (b-a+1) 2k+1>=(b−a+1) - 两边取对数(以2为底),得 k + 1 > = l o g 2 ( b − a + 1 ) k+1 >= log_2(b-a+1) k+1>=log2(b−a+1),最后得到: k > = l o g 2 ( b − a + 1 ) − 1 k >= log_2(b-a+1) - 1 k>=log2(b−a+1)−1
- 所以这里, k k k 只要需要取最小的满足条件的整数即可, b − a + 1 b-a+1 b−a+1 的取值为 [ 2 , n ] [2, n] [2,n],可以通过预处理把所有 k k k 求出来。
- 当 l o g 2 ( v ) log_2(v) log2(v) 为整数时, k = l o g 2 ( v ) − 1 k = log_2(v) - 1 k=log2(v)−1;否则 k k k 为 l o g 2 ( v ) − 1 log_2(v) - 1 log2(v)−1 的上整。
- C++ 代码实现如下:
for (i = 1; i <= n; i++) {
lg2K[i] = k - 1;
if ((1 << k) == i) k++;
}
- 进行查询的时候,可以通过 O ( 1 ) O(1) O(1) 的时间得到上述 k k k,即
int k = lg2K[b - a + 1]; - 查询的 C++ 代码实现如下:
int RMQ_Query(ValueType A[], int(*f)[MAXN], int a, int b) {
if (a == b) {
return a;
}
else if (a > b) {
a = a^b, b = a^b, a = a^b; // 交换 a 和 b 的值
}
int k = lg2K[b - a + 1];
return RMQ_MinIndex(A, f[k][a], f[k][b - (1 << k) + 1]);
}
- A A A 数组代表原数组, f f f 是个二维数组,即上文提到的动态规划数组。
4、RMQ 的 二维的扩展
- ST 算法可以扩展到二维,用四维的数组来保存状态,每个状态表示的是一个矩形区域中的最值,可以用来求解矩形区域内的最值问题。
- f [ i ] [ j ] [ x ] [ y ] f[i][j][x][y] f[i][j][x][y] 代表矩形区域 [ ( x , y ) , ( x + 2 i − 1 , y + 2 j − 1 ) ] [(x, y), (x + 2^i -1, y + 2^j-1)] [(x,y),(x+2i−1,y+2j−1)] 的最值,每个矩形的最值来自于四个子矩形的最值,这里先给出代码,然后通过注释配上图解来进行进一步讲解。
const int MAXM = 9;
const int MAXN = 301;
int RMQ_Pack(int r, int c) {
return (r << MAXM | c);
}
void RMQ_Init(ValueType A[MAXN][MAXN], int XLen, int YLen, int f[MAXM][MAXM][MAXN][MAXN]) {
int i, j, x, y, k;
for (i = 0; i < MAXM; i++) {
for (j = 0; j < MAXM; ++j) {
for (x = 1; x + (1 << i) - 1 <= XLen; ++x) {
for (y = 1; y + (1 << j) - 1 <= YLen; ++y) {
int &rf = f[i][j][x][y];
if (i == 0 && j == 0) {
rf = RMQ_Pack(x, y); // 1
}
else if (i == 0) {
rf = RMQ_MinIndex(A, f[i][j - 1][x][y], f[i][j - 1][x][y + (1 << (j - 1))]); // 2
}
else if (j == 0) {
rf = RMQ_MinIndex(A, f[i - 1][j][x][y], f[i - 1][j][x + (1 << (i - 1))][y]); // 3
}
else {
int a = RMQ_MinIndex(A,
f[i - 1][j - 1][x][y], // 4
f[i - 1][j - 1][x + (1 << (i - 1))][y + (1 << (j - 1))]); // 5
int b = RMQ_MinIndex(A,
f[i - 1][j - 1][x][y + (1 << (j - 1))], // 6
f[i - 1][j - 1][x + (1 << (i - 1))][y]); // 7
rf = RMQ_MinIndex(A, a, b);
}
}
}
}
}
}
- 预处理的过程和一维的情况一样,只不过把二层循环变成了四层循环,行数比较多,但是不要慌,都在我们可控范围内,我会根据注释来一行一行解释。
- 1)因为是二维,如果要存储下标就要存储两个值,而且返回也要返回两个值,所以这里采用了一个打包的方法,把两个整数打包成一个整数,具体实现见
RMQ_Pack(左移+位或效率优于乘法)。 - 2)
i==0的情况代表矩形X维长度为1,所以退化成一维的情况,看代码的时候可以忽略[i]和[x]来看; - 3)
j==0的情况代表矩形Y维长度为1,同样退化成一维的情况,看代码的时候可以忽略[j]和[y]来看; - 对于 4)5)6)7),这里我们画了一个图,如图二-4-1所示:
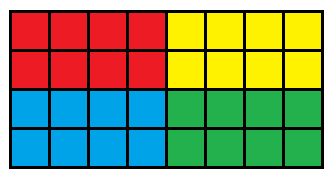
图二-4-1 - 4) f [ i − 1 ] [ j − 1 ] [ x ] [ y ] f[i - 1][j - 1][x][y] f[i−1][j−1][x][y] 代表 红色块;
- 5) f [ i − 1 ] [ j − 1 ] [ x + 2 i − 1 ] [ y + 2 j − 1 ] f[i - 1][j - 1][x + 2^{i - 1}][y + 2^{j - 1}] f[i−1][j−1][x+2i−1][y+2j−1] 代表 绿色块;
- 6) f [ i − 1 ] [ j − 1 ] [ x ] [ y + 2 j − 1 ] f[i - 1][j - 1][x][y + 2^{j - 1}] f[i−1][j−1][x][y+2j−1] 代表 黄色块;
- 7) f [ i − 1 ] [ j − 1 ] [ x + 2 i − 1 ] [ y ] f[i - 1][j - 1][x + 2^{i - 1}][y] f[i−1][j−1][x+2i−1][y] 代表 蓝色块;
- 是不是感觉到了 " 千言万语,不如画个图!"
- 文章结尾提供了二维 RMQ 的详细模板代码。
三、RMQ 的应用与扩展
1、离散化
【例题1】给定一个长度为 n ( n < = 100000 ) n (n <= 100000) n(n<=100000) 的单调不降序列 a [ i ] a[i] a[i],然后是 q ( q < = 100000 ) q(q <= 100000) q(q<=100000) 条询问,问给定区间 [ l , r ] [l, r] [l,r] 出现最多的数的次数。
- 首先对原数组进行一次离散化,即对于所有的数均设定一个组号,相同的数有相同的组号,存储在数组 h [ i ] h[i] h[i] 中,如下表所示:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| a[i] | -1 | -1 | 1 | 1 | 1 | 1 | 3 | 10 | 10 | 10 |
| h[ a[i] ] | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 4 | 4 | 4 |
- 然后将各个数的频率统计后记录在一个数组 c [ i ] c[i] c[i] 中,表示该类数的多少;
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| c[i] | 2 | 4 | 1 | 3 |
- 对于输入的询问 [ l , r ] [l, r] [l,r],直接查询它们在哪个组,分三种情况讨论:
- 1)如果 l l l 和 r r r 在一个组,那么最长长度就是 r − l + 1 r - l + 1 r−l+1;
- 2)如果组号相差 1,那么找出两者的分界点,取个数多的值;
- 3)如果相差大于 1,那么先将两头截掉,统计大的记录,再和中间那段的最大值比较大小,中间那段的最大值可以用 R M Q RMQ RMQ 区间查询最值。
2、逆序数问题
【例题2】小明有 n ( n < = 10000 ) n (n<=10000) n(n<=10000) 个宾馆的列表,每个宾馆有价格 p [ i ] p[i] p[i] 和 距离 d [ i ] d[i] d[i],对于宾馆 i i i,如果能够找到一个宾馆 j j j 同时满足 ( p [ j ] < p [ i ] 且 d [ j ] < d [ i ] ) (p[j] < p[i] 且 d[j] < d[i]) (p[j]<p[i]且d[j]<d[i]),那么 i i i 这家宾馆他就不会考虑,请给出小明的候选宾馆列表。
-
把 p [ i ] p[i] p[i] 和 d [ i ] d[i] d[i] 看成是二维平面上的点。如图三-2-1所示,红色的为候选列表,灰色的为淘汰列表。
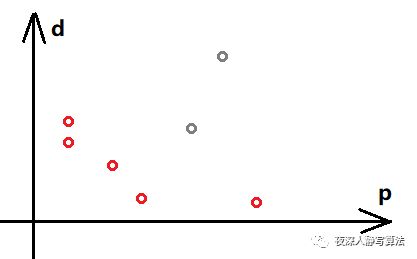
图三-2-1 -
比较直观的感觉就是,在 原点 和 当前点 组成的矩形中,如果没有其他点,那么它就能够作为候选列表。
-
那么,我们可以把宾馆数据按照 p [ i ] p[i] p[i] 递增排序,如果 p [ i ] p[i] p[i] 相等,则按照 d [ i ] d[i] d[i] 递减排序,对于某个 i i i ,如果所有的 j < i j < i j<i 都满足 d [ j ] > = d [ i ] d[j] >= d[i] d[j]>=d[i],则 i i i 就是一个候选宾馆。
-
再明确一点,规则可以转化成:如果所有的 j < i j < i j<i 中的最小值 d [ j ′ ] > = d [ i ] d[j'] >= d[i] d[j′]>=d[i],那么 i i i 就是一个候选宾馆。
-
于是,对 d [ j ] d[j] d[j] 数组预处理 R M Q RMQ RMQ 即可。
3、区间 GCD
【例题3】给定 n ( n < = 1 0 5 ) n(n <= 10^5) n(n<=105) 个数 a [ i ] a[i] a[i], Q ( Q < = 1 0 5 ) Q(Q<=10^5) Q(Q<=105) 次询问 [ l , r ] [l, r] [l,r] 区间内所有数的 g c d gcd gcd (最大公约数)。
-
在学习初等数论的时候,我们已经了解到 g c d gcd gcd 的定义如下:
g c d ( a , b ) = p 1 m i n ( x 1 , y 1 ) p 2 m i n ( x 2 , y 2 ) p 3 m i n ( x 3 , y 3 ) . . . p k m i n ( x k , y k ) gcd(a,b)=p_1^{min(x_1,y_1)}p_2^{min(x_2,y_2)}p_3^{min(x_3,y_3)}...p_k^{min(x_k,y_k)} gcd(a,b)=p1min(x1,y1)p2min(x2,y2)p3min(x3,y3)...pkmin(xk,yk) -
可以把问题转换成指数的最值问题, R M Q RMQ RMQ 求解;
-
状态转移方程如下:
f [ i ] [ j ] = { a [ j ] i = 0 g c d ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j + 2 i − 1 ] ) i > 0 f[i][j] = \begin{cases} a[j] & i=0\\ gcd(f[i-1][j], f[i-1][j + 2^{i-1}]) & i>0 \end{cases} f[i][j]={ a[j]gcd(f[i−1][j],f[i−1][j+2i−1])i=0i>0 -
这里 f [ i ] [ j ] f[i][j] f[i][j] 不再存下标,而是存了实际的 g c d gcd gcd 值;
-
查询的话,还是参考区间最小值的找最小重叠区间的方案;
4、二分枚举配合RMQ
- 当数组中一个区间的左端点固定,右端点不断变大的过程,势必会导致整个区间的最小值越来越小(或者不变,至少不会越来越大),所以这里存在单调性(单调不增),任何存在单调性的问题都可以通过二分枚举来把原本问题的时间复杂度从 O ( n ) O(n) O(n) 降到 O ( l o g ( n ) ) O(log(n)) O(log(n))。
- 来看一个例子:
【例题4】 n ( n < = 50000 ) n(n <= 50000) n(n<=50000) 个长度不同的数字 s [ i ] s[i] s[i] 排成一排,求最大的 j − i j-i j−i,对所有的 s [ k ] ( i < k < j ) s[k](i < k < j) s[k](i<k<j),都满足 ( a [ i ] < a [ k ] < s [ j ] ) (a[i] < a[k] < s[j]) (a[i]<a[k]<s[j])。
- 首先,我们来看朴素的做法;
- 枚举 i i i, 对于每个 i i i,枚举 j j j,然后判断 s [ i + 1... j − 1 ] s[i+1 ... j-1] s[i+1...j−1] 的最小值是否大于 s [ i ] s[i] s[i],从所有候选的 j j j 中,找到最大的 s [ j ] s[j] s[j],用 j − i j-i j−i 去更新最终答案,其中找区间最大值和区间最小值可以采用区间 R M Q RMQ RMQ,所以算法时间复杂度 O ( n 2 ) O(n^2) O(n2);
- n n n 的范围太大,所以这里肯定是要优化的;
- 考虑到固定 i i i 时,随着右区间的增大,区间最小值是有单调性的,所以对于 j j j 的枚举可以采用二分。
- 具体的,这个问题可以通过枚举 i i i,二分枚举 t t t 来解决,如果
s[ RMQMin(i+1, t) ] > s[i],则表示 t t t 还可以往大扩,找到一个最大的 t t t 以后,再用j = RMQMax(i+1, t);来获取 j j j,再用 j − i j-i j−i 来更新最大值,算法时间复杂度 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n))。
5、最长连续不重复子串
【例题5】给定 n n n 个数字 a [ i ] a[i] a[i],以及 m m m 次询问 [ l , r ] [l, r] [l,r] ( 1 ≤ n , m ≤ 200000 , 1 < = l < = r < = n ) (1 ≤ n, m ≤ 200000, 1<=l<=r<=n) (1≤n,m≤200000,1<=l<=r<=n),询问区间内的最长连续不重复子串的长度。例如 9 个数字的序列如下:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| a[i] | 2 | 5 | 4 | 1 | 2 | 3 | 6 | 2 | 4 |
区间 [ 1 , 6 ] [1,6] [1,6] 的最长连续不重复子串为 [ 2 , 6 ] = ( 5 , 4 , 1 , 2 , 3 ) [2,6]=(5,4,1,2,3) [2,6]=(5,4,1,2,3),长度为 5;
区间 [ 5 , 9 ] [5,9] [5,9] 的最长连续不重复子串为 [ 6 , 9 ] = ( 3 , 6 , 2 , 4 ) [6,9]=(3,6,2,4) [6,9]=(3,6,2,4),长度为 4;
区间 [ 5 , 8 ] [5,8] [5,8] 的最长连续不重复子串为 [ 5 , 7 ] = ( 2 , 3 , 6 ) [5,7]=(2,3,6) [5,7]=(2,3,6) 或 [ 6 , 8 ] = ( 3 , 6 , 2 ) [6,8]=(3,6,2) [6,8]=(3,6,2),长度为 3;
- 如果对于每个区间,都进行一次 哈希,总的时间复杂度为 O ( n m ) O(nm) O(nm),肯定是不行的;
- 对于每个数字 a [ i ] a[i] a[i],我们就可以通过一次预处理把下标小于它且离它最近的相同数的位置存下来,放到 pre[i] 数组中,如下:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| pre[i] | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 5 | 3 |
- 然后就可以通过这个数组来进行动态规划了,用 d p [ i ] dp[i] dp[i] 表示以第 i i i 元素结尾的最长连续不重复子串的长度,则有状态转移方程如下:
d p [ i ] = m i n ( d p [ i − 1 ] + 1 , i − p r e [ i ] ) dp[i] = min(dp[i-1] + 1, i - pre[i]) dp[i]=min(dp[i−1]+1,i−pre[i])
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| dp[i] | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 3 | 4 |
-
那么,当我们进行区间询问 [ l , r ] [l, r] [l,r] 时,对应所有的 i i i 满足 l < = i < = r l <= i <= r l<=i<=r,以 i i i 结尾的子串中,最长不重复子串的长度 x [ i ] x[i] x[i] 满足:
x [ i ] = { d p [ i ] i − d p [ i ] + 1 > = l i − l + 1 i − d p [ i ] + 1 < l x[i] = \begin{cases} dp[i] & i-dp[i]+1 >= l\\ i-l+1 & i-dp[i]+1 < l \end{cases} x[i]={ dp[i]i−l+1i−dp[i]+1>=li−dp[i]+1<l -
于是,我们再生成后一个辅助数组: i d p [ i ] = i − d p [ i ] + 1 idp[i] = i - dp[i] +1 idp[i]=i−dp[i]+1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| idp[i] | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 6 | 6 |
- 由于 d p [ i ] dp[i] dp[i] 比 d p [ i − 1 ] dp[i-1] dp[i−1] 最多大 1,所以 i d p [ i ] idp[i] idp[i] 一定是一个单调不降序列;
- 那么,当给定任意区间 [ l , r ] [l, r] [l,r],通过二分枚举可以找到 i d p [ i ] > = l idp[i] >= l idp[i]>=l 最小的 i i i,套用 x [ i ] x[i] x[i] 的公式,分两种情况讨论:
- 1) i d p [ i ] > = l idp[i] >= l idp[i]>=l , 找到最小满足这个不等式的 i,求 RMQ(dp, i, r) 的最大值;
- 2) i d p [ i ] < l idp[i] < l idp[i]<l ,当 i i i 越大, x [ i ] = i − l + 1 x[i] = i-l+1 x[i]=i−l+1 越大;
- 结合两种情况,得到 x [ i ] x[i] x[i] 最大值就是最后的答案;
- 本文所有示例代码均可在以下 github 上找到:github.com/WhereIsHeroFrom/模板/RMQ
![]()
四、RMQ 题集整理
| 题目链接 | 难度 | 解法 |
|---|---|---|
| Balanced Lineup | ★☆☆☆☆ | RMQ 模板题 |
| HDU 1806 Frequent values | ★☆☆☆☆ | 离散化 + RMQ |
| HDU 6098 Inversion | ★★☆☆☆ | 分段统计 + RMQ |
| HDU 3183 A Magic Lamp | ★★☆☆☆ | 鸽巢原理 |
| HDU 5289 Assignment | ★★☆☆☆ | 二分 + RMQ / 单调队列 |
| HDU 3530 Subsequence | ★★☆☆☆ | 二分 + RMQ / 单调队列 |
| PKU 2452 Sticks Problem | ★★☆☆☆ | 二分+RMQ |
| HDU 3193 Find the hotel | ★★☆☆☆ | 逆序数 |
| HDU 6406 Taotao Picks Apples | ★★★☆☆ | 二分 + 动态规划 + RMQ |
| HDU 5247 找连续数 | ★★★☆☆ | HASH + RMQ |
| HDU 5172 GTY’s gay friends | ★★★☆☆ | RMQ, 卡内存过不了,线段树求解 |
| HDU 3486 Interviewe | ★★★☆☆ | 枚举 + RMQ |
| HDU 4252 A Famous City | ★★★☆☆ | 离散化 + RMQ |
| PKU 2201 Cartesian Tree | ★★★☆☆ | 构造笛卡尔树 |
| PKU 2019 Cornfields | ★★★☆☆ | 二维RMQ |
| ZJU 2859 Matrix Searching | ★★★☆☆ | 二维RMQ |
| HDU 2888 Check Corners | ★★★☆☆ | 二维RMQ |
| HDU 2305 WorstWeather Ever | ★★★★☆ | 二分+RMQ |
| PKU 3419 Difference Is Beautiful | ★★★★☆ | 动态规划 + RMQ |
| HDU 4123 Bob’s Race | ★★★★☆ | 树形DP + RMQ / 单调队列 |
| HDU 5696 区间的价值 | ★★★★☆ | 单调队列 + RMQ |
| HDU 5726 GCD | ★★★★☆ | RMQ 的 GCD 变种 |
| HDU 5371 Hotaru’s problem | ★★★★☆ | Manacher + RMQ |
| HDU 2459 Maximum repetition substring | ★★★★☆ | 后缀数组 + RMQ |
| HDU 3948 The Number of Palindromes | ★★★★☆ | 后缀数组 + RMQ |
| HDU 5558 Alice’s Classified Message | ★★★★☆ | 后缀数组 + RMQ |
