HDL4SE:软件工程师学习Verilog语言(一)
1 引言
1.1 Verilog语言的基本概念
建议软件工程师,特别是嵌入式或者驱动软件设计方面的工程师,对硬件应该有一定的了解。这里所说的硬件,一般可能理解为类似于DIY组装计算机,笔记本换硬盘,升级内存,升级CPU,制作网络线,使用万用表或示波仪测量信号,用电烙铁换板子上的电阻电容,显卡超频,手机贴膜,… ,这些似乎都应该懂一点才是。然而这里讲的与编程相关的硬件,特别指数字电路,这是因为软件与硬件的接口,主要是数字电路。对数字电路方面有一定的了解,有助于与数字电路工程师交流,理解数字电路的工作原理,做出高效的驱动软件,作为数字电路的第一用户,能够为数字电路设计提出要求和建议。哪怕不是嵌入式或者驱动软件工程师,也应该对硬件了解多一点,比如DDR,Cache,PCIE总线,指令集等方面,对它们的实现和接口有比较深入的了解,知道自己编的程序最终是如何运行起来的,依赖什么样的硬件在运行,对软件设计是有帮助的,会有意识地使用一些高效的编程模式,避开一些看着简单,实际上非常耗费资源的编程习惯。
本文试图从软件工程师的角度,介绍硬件描述语言–Verilog语言。这种语言是用来描述硬件的,功能非常强大,可以支持电路的概要设计(行为级描述),有点象软件中的流程图设计、数据流设计或者通信协议设计,非常抽象地描述顶层模块之间的通信与同步,保证顶层模块之间的逻辑正确性;可以支持所谓的寄存器传输级的描述,这可以看作数字电路详细设计,对应到软件中是高级语言编程实现;可以支持到门级设计,对应到软件中是汇编语言编程;甚至可以支持到开关级设计,这个与电路的物理实现相关了,软件中已经没有对应的设计了,勉强可以对应到微码设计,指令集用微码来实现的平台,微码编程应该是软件工程师能接触的最低级别了。软件工程师至少应该能看懂这种语言的RTL描述,甚至能够设计并实现一些小的模块。本文不是一个完全的Verilog语言的参考手册,只是着重描述了软件工程师需要了解的硬件描述语言相关的部分内容,基本上关注在RTL级别,少量涉及门级。完整的语言参考,请参照IEEE.1364-2005 Standard for Verilog Hardware Description Language。
由于Verilog是一种硬件描述语言(HDL),很多软件工程师可能觉得它离工作比较远,运行方式迥异,不大愿意学习。其实不管如何,Verilog就是一种计算机语言,同样有数据类型,有顺序,分支,循环等控制结构,有赋值语句,表达式,优先级控制下的四则运算。有编译(数字电路工程师称之为综合),有目标平台(各种FPGA,CPLD或者是某种平台的工艺库,一般不叫指令集)。
作为一种硬件描述语言(HDL),verilog的编译(综合)的结果是某个目标平台下的电路。所谓电路,就是该平台下各种基本单元(cell) 以及单元之间的的连接。目标代码(电路)的执行是完全并发的,也就是各个基本单元完全并发执行。
verilog语言数据结构比较简单,基本的数据就是bit位,没有指针,没有结构,联合之类c语言中的复杂数据结构,数组虽然有,但是其实用得不算多,没有内存,也没有内存管理。参与计算的数据其实就是若干个二进制位。verilog按位操作数据,也可以将若干位数据当成一个整数参与计算,理论上可以操作从一位到任意位的数据,并且可以从中间抽取任意范围的位,也可以将若干个数据中的位组成一个新的数据。
verilog中常用的控制结构是分支,包括if分支和case分支,顺序结构其实只是一种临时的描述方法,最终编译的结果本身没有顺序的概念,电路全并发执行,不存在执行意义上的先后顺序。循环语句很少使用,真要用在编译时也是全部展开,然而电路的运行,其实是真正的循环。
c语言的主要程序结构是函数以及函数之间的调用,verilog的基本程序结构是模块(module)以及模块之间的连接关系,模块对外是输入端口和输出端口,模块内部可以有其他模块的实例,如果把基本单元也作为一种模块(事实上很多工艺平台就是把基本单元描述成模块的),那模块内部的结构本质就是子模块以及子模块之间的连接关系。所谓的表达式,分支,赋值无非是描述子模块以及之间的连接关系。
1.2数字电路概述
1.2.1 真值表与查找表
数字电路的数学基础,是形式逻辑,或者说是形式逻辑中的命题逻辑部分。形式逻辑也称为数理逻辑或符号逻辑。这里的符号是一段变化的信号,没有变化无法形成符号。最简单的变化就是从高到低和从低到高的变化了,因此最简单的符号集合至少要包括两个符号,这样才能产生变化,我们记这两个符号为0和1。这两个符号的若干组合,可以构成其他符号,我们可以用英文字母表和数字来表示每个符号。假如我们对一个信号源(比如天文射电望远镜收到的信号)一无所知,从中得到的一连串符号,是否是正在向我们传送某种信息,还是是毫无意义的噪声?符号逻辑就是琢磨这个的,基本的想法是,有意义的东西都是由比较简单的规则形成的,因此如果能够从信号源的符号序列中找到背后的规则,这些规则又比较简单而且一致,那么这个信号源可能是有意义的。更加深入的介绍就扯远了,这里就不接着深入下去了。
符号逻辑的研究,建立了一个形式化系统,这个系统符合人类的逻辑推理规律,其中一个重要的结果是,有一组规则(记为L),形成的所谓有意义的符号序列能够用布尔运算来进行解释(赋予语义),并且可以证明布尔运算与符号逻辑中的L系统完全等价,这样一来,布尔运算就有了数学理论基础,L系统也可以方便地用布尔运算来研究。所谓的布尔运算,其实就是二进制的计算,就是数字电路的基础。
布尔运算中,基本的符号就是0和1,一个运算可以视为定义在这两个符号上的函数,按照函数的定义,一个函数是从定义域到值域的映射,一组自输入的组合对应一个唯一的值域中的值,因此一个函数可以由所有输入的组合对应的值来唯一确定,这个枚举每一组输入形成的输出的表格,称之为真值表。一元函数有四个,f0=0, f1(x)=x,f2(x)=~x, f3=1表示非运算,对应的真值表是:
| x | f0 | f1 | f2 | f3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
二元函数有16个,
| xy | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | fa | fb | fc | fd | fe | ff |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 01 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 10 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 11 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
其中f0常数函数0, ff常数函数1,f7为或运算, f1为与函数, f6为异或函数,f8为或非函数,fe为与非函数,fd为蕴含函数(也称为如果那么函数)等都是常用的布尔运算,
n元函数的真值表有2的n次方行,总共有2的(2的n次方)次方个函数。
对超过二元的多元函数,总是可以用元比较少的函数的复合函数表示,比如3元函数
f(x,y,z)=g(x, h(y,z)),也就是说,一个三元函数,总是可以用两个二元函数的复合函数表达出来(如何证明?)。
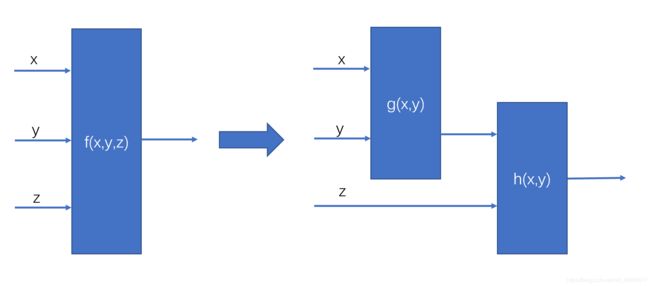
数字电路中的基本单元,无非是表达某个函数,FPGA中实现的基本单元,其实就是记住真值表并实现了查表电路,FPGA给真值表加查表电路取了个名字叫查找表(LUT:look up table)。FPGA开发工具的一个重要任务就是生成每个基本单元的真值表,写到FPGA中对应的基本单元的存储器中,实现对应的功能。
理论上,实现一个32位浮点的乘法器,可以定义32个真值表,每个真值表表示一个64元函数,对应到输出结果的每一位。然而,一个64元函数的真值表有2^64行,也就是说需要这么多位才能存储。为了实现这么个函数存储这么多位,显然不现实。因此多元函数在实现时基本上是由输入比较少的函数复合而成。一般FPGA中最多可能提供8输入的LUT单元,实际实现时则以2,3,4输入的居多。
用LUT实现基本单元可以提供FPGA的现场可编程的功能(FPGA:现场可编程门阵列),对FPGA下载不同的真值表,就可以定义不同的功能,FPGA中一般还提供了多输入的复杂而又常用的基本单元,比如9位乘法器(DSP单元),这已经不是真值表定义了,这是所谓的全定制单元,实现效率非常高。
真值表实现方式效率是比较低的,想想看实现一个与运算的二元函数,就需要记住4位二进制,或者反过来说,为了实现一个与运算,需要能够实现所有二元函数的资源,并且还得有个查表电路,效率肯定很低。要是用真值表实现两个32位浮点的乘法,那等于用能够实现所有64元函数的资源实现了其中的一个函数,这效率肯定低得可怕,实际上已经无法接受了。好像真值表存储与电路实现之间不对称了啊,都是实现同样的功能,真值表需要的资源似乎很多。其实问题的根本在于,一个特定的真值表并没有携带那么多的信息,如果真值表能够以某种无损压缩方式存储,附带上解码电路,需要存储的信息就要少很多了。这里似乎发现了一种数据无损压缩的方法,把一组数据(比如4K位)视为一个真值表,将其对应的电路简化后用某种方式存储起来,是不是一种数据压缩方式啊。解码的方法就是实现这个电路,然后计算出这个真值表,甚至可以随机读取压缩结果中的任意位呢,只要在实现电路的输入给出这一位对应的组合,输出就是相应的位,ROM表是否也可以这么实现?嗯,不知道是否已经有类似的办法了,如果没有,还真值得琢磨琢磨。
在ASIC设计中提供的基本单元就更加基础一些。布尔运算理论中有个所谓运算完全组的概念。一个运算完全组,就是一组函数,其他的所有函数都可以用这组函数中的函数复合表示出来。显然一元函数是无法构成运算完全组的,{与,非}, {或, 非},{如果那么, 非},{与非}, {或非}等组合都是运算完全组。有意思的是,除了{与非}和{或非}之外,其他的二元函数都不能单独构成运算完全组(有单个三元函数能构成运算完全组吗?)。{非}, {与,或}, {非,异或}等都不是运算完全组(证明一下看看?)。运算完全组的概念非常重要,意味这所有的函数都可以用运算完全组中的函数复合而成,也就是说,一个复杂数字电路总是可以用非常少的基本单元组合而成。上面的结论表明,单独的与非运算(与非门)和或非运算(或非门)都可以复合出任意一个布尔运算函数,所以一个数字电路平台理论上可以全部由与非门或者或非门组成,只买一种74LS00(四个2输入与非门)芯片,就可以搭出所有的二进制运算函数。当然实际实现时,还是要考虑实现的效率,理论上可以用与非门实现一个非门,然而真要这么做,电路上肯定浪费了。所以ASIC中的基本单元也提供了相对来说更加多的选择,一般的非门,与门,或门,与非门,或非门等都提供的,甚至还提供三输入或四输入的与或非门单元,有的工艺库的基本单元甚至提供了全加器,包括4位全加器等单元。
有了布尔运算,算术运算也一样可以表达出来,说起来算术运算无非是结果的每一位用一个函数计算出来就是了,比如两个1位数加法,结果表示为进位和一位加结果
s的加法口诀(真值表):00得0, 01得1,10得1,11得0,就是异或运算(不相等运算)嘛。进位c的加法口诀:00得0, 01得0, 10得0, 11得1,就是与运算。如果还要考虑本身有下级进位输入,那就构成一个三输入的加法器,称位全加器。真值表如下(cc表示下级进位,c表示本级进位):
| a | b | cc | s | c |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
多位加法运算可以用全加器连接起来实现,比如4位全加器:

这个四位全加器也可以级联起来,实现位数更多的加法器。
除了常规意义的运算之外,if语句也可以用函数表达出来,其实就是一个选择表达式(C语言中的? : ) c?a:b无非就是一个三元函数,真值表如下:
| c | a | b | c?a:b |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
switch(case)语句可以解释为if语句的嵌套,这样,一个很复杂的表达式,包括if语句在内,都可以用基本的单元表达出来。
其实早期的ASIC工具,就是一个门级设计的绘图工具,可以选择基本单元库中的基本单元(各种门,全加器等),然后将它们的输入输出按照设计要求连接在一起。这个有点象早期的软件设计,汇编语言是比较重要的语言,现在大家都越来越往高处走了,比如流行用python语言,c语言都看不上了啊。
1.2.2 组合电路与时序电路
在实际的电路中,只有函数或者真值表是不够的,至少有两个方面的原因:第一方面是有按某个序列生成信号的需求,比如显示控制电路,要求按照逐行,行内逐个像素来生成控制信号,以便控制显示器实现显示功能。这其实是显示器的物理特征造成的,我们不大可能在显示器的每个像素后面接上一条独立的控制线,来生成该像素的亮度。实际实现是都是用一个比较快的频率扫过每个像素,逐点给出扫过的像素的亮度,从而实现显示功能,尽管扫描时一个一个像素进行的,但是如果扫描频率足够快,给人的感觉是生成一幅完整的稳定的画面,不知道鸡,猪,猫,狗,鹰,蛇,蜂,蚁之类的动物看我们的显示器是什么感觉,会不会感觉头晕。这种逐点扫描的需求就需要按照扫描的顺序和速度,来生成相应的信号,这样的信号所蕴含的序列特征,要求信号产生器必须拥有某种记忆能力,至少要记住当前扫描的位置,从而决定下一个扫描的位置。这种带记忆的电路,本质上已经不是一个函数能够描述的了,电路的输出不是由输入完全决定,还跟内部记忆的内容(内部状态)相关,内部记忆的内容也可能根据输入和前面的记忆进行修改,也就是说,输出跟输入的历史相关,是一个输入的时间序列函数,而不是简单的当前输入决定的函数,这样的电路称为时序电路。与之对应,仅仅实现函数功能的电路,其输出完全由输入决定,这样的电路叫组合电路。
第二个方面的原因来自于电路的延迟,一个组合电路中的每位输出由于从输入到输出的路径不一样,延迟时间不一样。延迟来自于两个部分,一个部分是电路单元的延迟,一个部分是单元之间的连接线的延迟。这种延迟不完全是电磁波传输速度导致的,从物理模型上,电路单元和连接线都可以初略地等效于一个电容/电阻的电路(RC),输入信号进入电路单元,到输出信号稳定,中间可以理解为要对等效的电容充放电,充放电到一定程度时,输出才是有效的,充放电的速度比电磁波传输的速度要慢很多。由于不同路径导致延迟时间不一致,就造成输出信号不断跳变,在输入信号稳定后,要过一段时间之后,输出信号才能稳定下来,变成一个正确的输出值,这段时间称为信号的建立时间。输入信号变化后,会经过一段时间,输出信号才会变成不稳定状态,这段时间称为信号的保持时间。我们只能在输入信号有效后,至少等待建立时间,并在信号保持时间内进行信号采样,才能得到正确的输出值。如果输入的信号是很多位,我们还需要保证输入信号也基本上同步地到达稳定状态。此时,一个可行的办法是,在输出信号有效的时间内,将输出的信号锁存在可以存储状态的电路单元中。这种单元称为寄存器,寄存器一般可以在一个控制信号的沿(从低到高或从高到低转变的过程)对其输入进行锁存(这是寄存器实现的物理特性决定的)。寄存器的输出则由输入决定,当然从锁存到输出稳定也有个寄存器输出信号的建立时间。
一般的做法是,用一个周期性的方波信号,来作为寄存器锁存的控制信号,在一个方波周期的上升沿(或下降沿),寄存器开始锁存输入信号,然后经过寄存器建立时间,寄存器开始输出稳定的信号,这些输出的信号又经过一系列复合函数计算(组合电路),经过一段时间后,生成稳定的信号,在下一个周期又锁存到寄存器中。信号就是这样从寄存器输出,结合外部输入信号,生成新的信号,然后锁存到寄存器中。这就是所谓的RTL描述,从一组寄存器出发,经过组合电路,锁存到另一组寄存器中,在前面所说的周期性的方波信号的控制下,不断循环往复。只要保证从寄存器到寄存器之间的每条组合电路路径建立时间少于方波的周期,也就是说确保在下一个方波上升沿到达之前组合电路能够输出有效的信号,我们就可以在寄存器中锁存正确的结果。这个周期性的方波信号一般称为时钟信号,其频率就是我们计算机中经常讲的主频。显然主频越高,组合电路的长度(直接影响延迟)就必须越短,所有寄存器之间组合电路的延迟,都必须小于时钟信号的周期,才能确保计算的正确性。除了时钟信号之外,一般还会有一个复位信号,用来控制寄存器的初始值。寄存器一般需要有初始值,就是电路上电之后,由系统统一给所有电路单元一个复位信号,在复位过程中寄存器被锁定一个指定的值,给出一个电路的初始状态,这样才能确保后面的变化过程中正确地实现需求的意图。
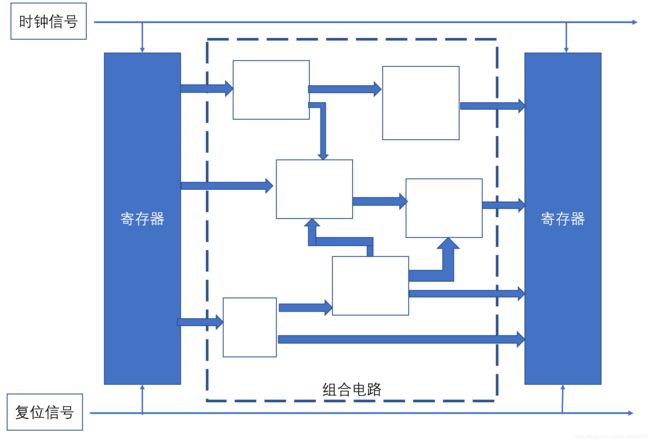
描述到这种级别的电路,称为RTL描述。
当然电路中寄存器可以是多级的,有些寄存器在不同的级中也可以是共享的,逻辑上都是寄存器->组合电路->寄存器->组合电路->…这么个结构。
这样的电路,在硬件上是可以实现的,跟概念级描述不一样,概念级描述一般可以用软件模拟(仿真),但是很多编译工具不支持到硬件实现, RTL描述是可以编译(综合)成为实际的FPGA或者ASIC电路的。因此后面的Verilog介绍中,我们着重介绍RTL的描述,重点描述RTL描述是如何用Verilog来完成的。
其实这种RTL描述方式,软件上也是经常用的,比如通信协议,SCSI访问协议,编译系统中的语法状态机描述,有限状态机都可以用这种方式描述。在每个周期中,根据状态和输入,进行计算,得到新的状态和输出,这是很常见的软件处理模式。
从下次开始,我们将从软件工程师的视角出发,详细地介绍Verilog语言RTL描述。